基于六棱台全张量磁梯度探头的目标定位方法*

丁 彪 胡 迪 于振涛

（1.海军航空大学教务处 烟台 264001）（2.海军潜艇学院遥感所 青岛 266041）

1 引言

海洋中的舰船目标大多由钢铁等材料建造而成，放置于地磁场中会发生磁化，从而改变原地磁场的分布，磁性目标定位技术［1～2]通过测量目标磁化产生的磁场而对目标进行定位。目前常见的磁传感器主要有磁阻磁力仪、光泵磁力仪和磁通门磁力仪等，随着测量技术的发展，超导磁力仪作为一种高灵敏度的磁场测量仪器得到了迅速的发展，利用超导磁力仪来搭建全张量磁梯度探头也得到了研究，吉林大学的申茂冬［3～4]对基于超导磁力仪的五棱台式全张量磁梯度探头进行研究，提出了一种五棱台侧面倾角的优化方法。李萌［5]对基于超导磁力仪的全张量探头的结构进行设计，提出了一种六方金字塔形的探头结构。海军工程大学的赵建扬［6]对基于超导磁力仪的全张量磁梯度探头存在的不平衡度干扰进行补偿，取得了较好的效果。

由目前的研究进展可以看出，目前基于超导磁力仪的全张量磁梯度探头尚处于系统的搭建阶段，缺乏相关的关于目标的定位方法的研究，本文提出了一种基于六棱台全张量磁梯度探头的磁性目标定位方法，首先建立了六棱台传感器分布的几何模型，然后计算了传感器测量值与磁梯度张量值之间的关系，最后提出了目标定位方法。最后通过仿真实验分析，对本文提出的基于六棱台全张量磁梯度探头的定位方法进行验证。

2 基于磁梯度张量的定位方法

2.1 磁梯度张量测量原理

全张量磁梯度探头中单个超导磁力仪的测量值为当地地磁场与目标产生的磁场两个矢量之间的叠加，由于地磁场的梯度很小（最大为0.02nT/m），远小于目标产生的磁场梯度，因此可以通过对测量值进行差分来消除地磁场的干扰，因此计算得到磁梯度张量主要由目标引起。

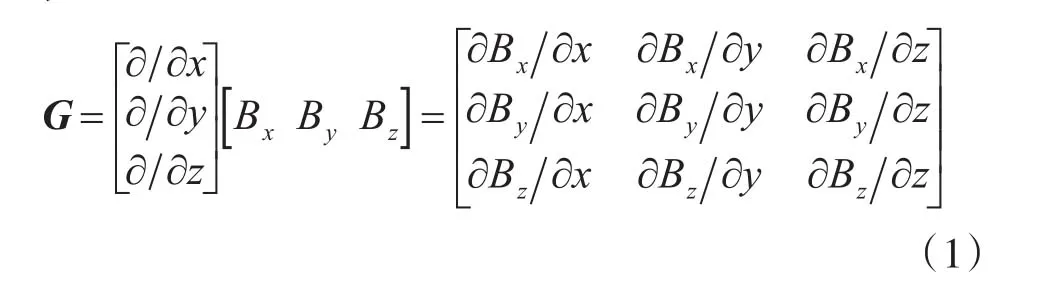
式中，G为磁梯度张量，B为磁场的矢量值。

2.2 六棱台全张量磁梯度探头的几何结构与测量原理

六棱台式全张量磁梯度探头由六个平面超导磁梯度计和三个超导磁强计构成，其几何结构示意图如图1所示，由图1所示，六个平面超导磁梯度计分别布置于六棱台的六个侧面上，平面超导磁梯度计的测量基线位于侧面上下两个边中点的连线上，利用六个平面超导磁梯度计的测量值可以求得磁梯度张量的各个分量，三个超导磁强计放置于六棱台的顶面上，其中磁强计的测量轴线两两正交。

图1 六棱台式全张量磁梯度探头几何结构图

下面通过六个平面的超导磁梯度计来计算磁梯度张量的值，建立笛卡尔三轴正交坐标系如图2所示，OX轴与OY轴放置于六棱台的底面位置处，坐标原点O位于底面的中心点位置处，OZ轴垂直于底面向上，对六棱台的六个侧面分别进行编号，记作i，取值依次为1、2、3、4、5、6，每个侧面的正交坐标系如图2所示。i号侧面与底面之间的夹角记为θi，i号侧面上的坐标系oxi轴在底面上的投影与OX轴之间的夹角为φi，由此可以得出坐标系OXYZ与i号侧面坐标系oxiyizi之间的关系如下所示：由此可得i号侧面上测量的磁场梯度与六棱台探头测量的磁梯度张量各个分量之间满足的关系如下：

图2 直角坐标系示意图

式（3）中，Gi为i号侧面上测量的磁场梯度，BX、BY、BZ分别为探头坐标系OXYZ下的磁场三分量，BXX、BXY、BXZ、BYY、BYZ分别为探头坐标系OXYZ下的五个相互独立的磁梯度张量分量，则由式（3）可得，通过6个侧面可以列出6个关于磁梯度张量各个分量的一次方程，而磁梯度张量的9个分量当中只有5个是独立的，因此可以列出关于磁梯度张量5个独立分量的线性方程组，通过求方程组可以得到磁梯度张量各个分量的最小二乘解。设通过6个侧面上测量的磁场梯度与六棱台探头测量的磁梯度张量分量之间建立如下关系：

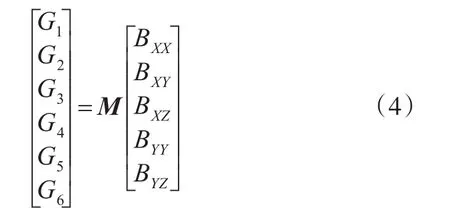
则上式中，M为6×5的参数矩阵，矩阵中各个元素的值与角度θi和φi有关，由式（4）求广义逆可以求得磁梯度张量的5个独立分量。

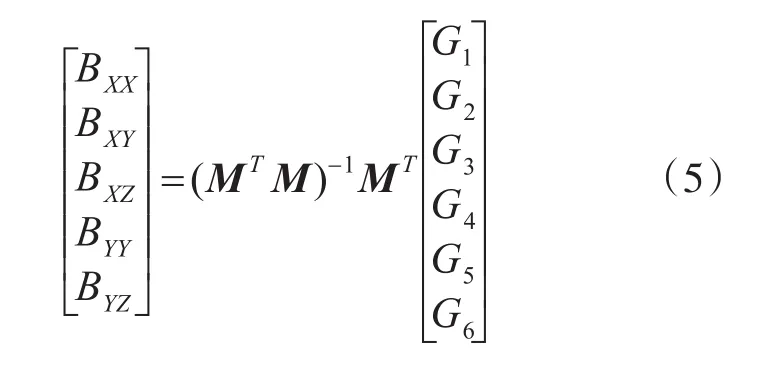
由式（5）可以求解出磁梯度张量的各个分量值。

2.3 六棱台全张量磁梯度探头的定位原理

目前较为常见的一种定位方法是Nara提出的基于欧拉反演的定位方法［7-12]，该方法的目标位置计算公式如下所示：

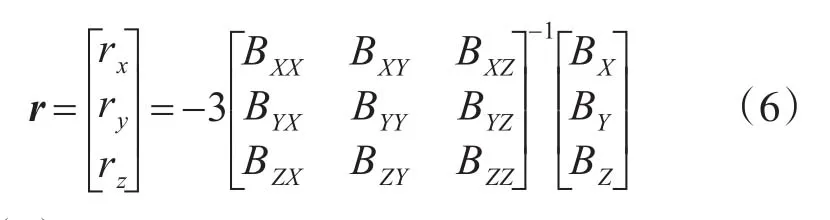
式（6）中，通过测量目标产生的磁梯度张量和磁场的三个分量可以实时得到目标的位置，实现对目标的定位。由式（5）可得，利用探头测量值可以计算得到磁梯度张量的9个分量，同时图1所示，六棱台的顶面上有三个超导磁强计可以测量磁场的三个分量，因此六棱台全张量磁梯度探头可以实现对目标的实时定位。

3 基于六棱台全张量磁梯度探头的目标定位仿真

根据Nara提出的基于欧拉反演的定位方法，利用本文所述的六棱台全张量磁梯度探头，对磁性目标的定位进行仿真分析，假设在不考虑磁场噪声的情况下，影响目标的定位精度的因素主要有：1）探头与目标之间的距离；2）超导磁强计的精度；3）平面超导磁梯度计的基线长度。

首先设定仿真的初始条件如下所示：建立如图2所示的直角坐标系OXYZ，假设磁性目标的磁矩为m=(1000，-30000，20000)Am2，目 标 位 于Z=27m的平面上，假设目标沿着直线Y=8m的直线平移，平面超导磁梯度计的基线长度设为10cm，超导磁强计的精度为1pT。

1）探头与目标之间的距离对目标定位误差的影响

按照初始条件下对目标定位进行仿真，仿真结果如图3所示，由图3可得，当目标距离探头较近时，定位误差相对较小，随着探头与目标之间的距离增加，定位误差的波动不断增大，因此对于远距离的目标，六棱台全张量磁梯度探头的定位误差较大。通过初始条件下的仿真分析可得，六棱台全张量磁梯度探头可以实现对目标的精确定位。

图3 原始条件下探头对目标的定位误差

2）超导磁强计的精度对磁性目标定位误差的影响

为了仿真分析超导磁强计的精度对目标定位的影响，将精度由1pT提高到0.1pT，其余的仿真条件不变，仿真分析目标的定位误差如图4所示。

图4 超导磁强计的精度对目标定位误差的影响

由图4可得，当超导磁强计的精度提高到0.1pT时，目标的定位误差显著减小。精度为0.1pT的定位误差始终小于精度为1pT的定位误差，且精度为0.1pT的定位误差最大为3.7m，因此可以得出，可以通过提高超导磁强计的精度来实现对远距离目标的精确定位。

3）平面超导磁梯度计的基线长度对磁性目标定位误差的影响

为了仿真分析平面超导磁梯度计的基线长度对目标定位的影响，将平面超导磁梯度计的基线长度由0.1m减小到0.08m，其余的仿真条件不变，仿真分析目标的定位误差如图5所示。

由图5可得，当平面超导磁梯度计的基线长度减小到0.08m时，对近距离目标的定位误差没有明显的变化，而对于远距离的目标定位误差波动较大。而平面超导磁梯度计的基线长度为0.1m时，对于近距离和远距离目标的定位误差波动都较小，因此，平面超导磁梯度计的基线长度越长，对远距离目标的定位精度越高。

图5 平面超导磁梯度计的基线长度对目标定位误差的影响

4 结语

本文提出了一种基于六棱台全张量磁梯度探头的磁性目标定位方法，该方法首先建立了六棱台传感器分布的几何模型，然后利用超导磁力仪和超导磁梯度计构建六棱台全张量磁梯度探头，通过六个侧面的超导磁梯度计测量值求得磁梯度张量的各个分量值，最后通过单个测量点的磁梯度张量与磁场测量值实现对目标的定位。文章最后设计了仿真实验对本文提出的六棱台全张量磁梯度探头的磁性目标定位方法进行仿真验证，仿真结果可得，本文提出的定位方法定位精度高，影响定位效果的主要因素为超导磁力仪的测量精度和探头与目标之间的距离。