基于DSP28335的惯导解算设计与优化*

杜伟伟 许江宁 何泓洋

（海军工程大学电气工程学院 武汉 430033）

1 引言

惯性导航系统（Inertial Navigation System,INS）是以牛顿经典力学为依据的自主式导航系统，只需要对惯性测量单元（Inertial Measurement Unit,IMU）输出结果进行积分就能得到导航信息。目前惯性导航系统常见做法是采用嵌入式DSP（Digital Signal Processing,DSP）或者FPGA（Field-Programmable Gate Array,FPGA）实现积分以及导航解算。DSP在嵌入式领域具有体积小，功耗低，计算能力强等特点多用于复杂计算系统中处理数字信号灯问题。DSP是TI(Texas Instruments,TI)公司于20世纪80年代设计制作的专用于数字信号处理的专用芯片。得益于其对数字信号处理能力强于其他CPU或微处理器，因此在通讯系统，信号处理系统，自动控制系统，航天、航空、军事等领域得到广泛应用。本文介绍了基于DSP 28335平台多种优化方法，本文提出程序设计优化技巧以及DSP特有优化方式。通过多种优化方式提升系统整体性能。

文献［1～6]重点介绍了DSP环境下C语言编程优化方式，从数据类型，数据操作以及变量定义方向进行优化，在语言优化其他方面稍有不足不能完全发挥DSP性能优势；文献［7～9]提出基于高性能DSP平台和FPGA平台共同完成捷联惯性导航系统的设计，利用FPGA对硬件时序控制优势采集信号，将数字信号通过特定接口输出至DSP芯片，由DSP芯片完成算法，实现高频、高速的惯导解算。由于文献中系统采用FPGA以及高性能DSP芯片导致系统硬件成本较高，在对成本有一定要求的系统中使用会受到限制。

因此，本文针对DSP 28335平台针对有限的系统资源进行优化问题，开展了程序设计以及优化方面的研究，对捷联惯导解算程序进行了优化。从而提升了程序运行效率。可以通过较低的硬件成本，实现惯导高速、高频解算。

2 捷联惯导系统基本理论

2.1 坐标系定义

对文中实际提到的坐标系统定义如下：

1）地心惯性坐标系统（i系）：坐标系原点位于地球中心O，xi轴指向地球春分放向，zi轴为地球自转轴，yi、xi、zi轴构成右手坐标系。

2）地球坐标系（e系）：与地球固定。原点位于地心，xe轴穿过地球赤道和本初子午线交点，ye穿过地球东经90°子午线与赤道交点，ze轴川渝地球北极点。

3）导航坐标系（n系）：坐标原点O位于载体质心，xn、yn、zn分别指向载体所在地的东、北、天。

2.2 惯性导航力学编排

捷联惯导系统是一种将加速度计和陀螺仪直接固定在载体上的一种惯性导航系统，计算机根据载体固定的加速度计测量线性运动信息和陀螺仪测量的角运动信息解算出载体的速度、姿态、运动方向、以及载体位置信息。图1为捷联式惯性导航系统工作原理图。

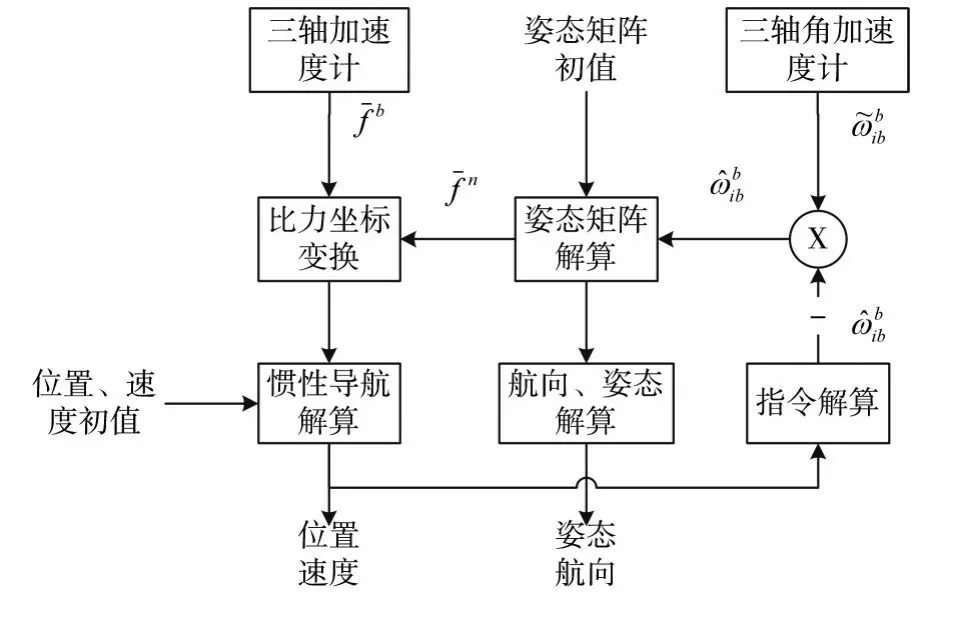
图1 捷联式惯性导航系统工作原理图

导航计算原理根据固定在载体的陀螺和加速度计所输出的角运动信息和线运动信息进行计算，角运动信息计算得出姿态转移矩阵，线运动信息输出的比力减去误差速度得到载体运动速度，经过姿态转移矩阵，将速度转为导航坐标系下，进行导航解算就能得到速度、姿态以及位置坐标信息。

惯性导航系统基本解算方程有速度更新、位置更新、姿态更新。姿态更新解算方法目前主流的有四元数姿态更新法、欧拉角法、等效旋转矢量法［10]。由于四元数姿态更新法相比其他算法计算量小，避免万向节死锁和奇异点的问题出现［11]。

惯导解算包括位置解算、速度解算与姿态解算。如下所示。

位置解算方程：

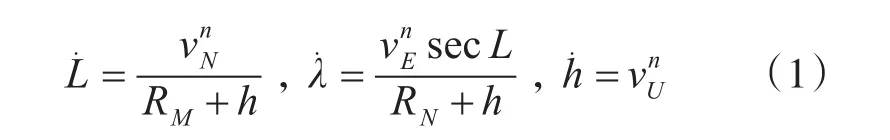
其中L、λ、h分别为载体所在位置的地理坐标系的纬度、经度、高度，vn为载体所在导航坐标系速度，为向东速度为向北速度为向天速度。

速度解算方程：

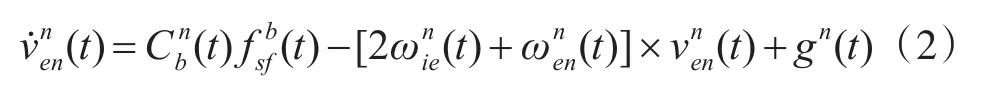
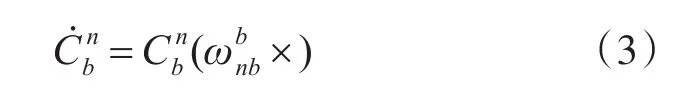
2.3 四元数姿态更新方法

四元数旋转可以避免欧拉角中万向节锁现象，而且只需要一个四维的四元数即可实现任意绕过原点的向量旋转，在某些情况下比旋转矩阵效率更高。四元数相比欧拉旋转可以实现球面平滑插值［12]。

2.3.1 四元数定义

四元数表示姿态，就是用四个元构成的数，可以表示为

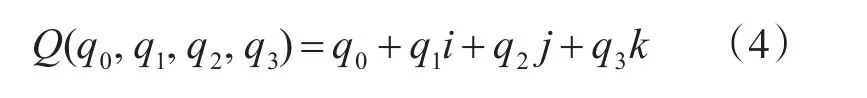
其中q0、q1、q2、q3为实数，q0为四元数的实部，qv=q1i+q2j+q3k为四元数的虚部。i、j、k是具有互相正交关系的单位向量同时又是虚单位四元数可以看做是复数的扩充，有的地方称为超复数。四元数之间运算规则满足加法交换律和加法结合律，但不满足乘法交换律也不满足乘法结合律。

2.3.2 欧拉角与四元数

分别定义俯仰角、偏航角、横滚角为绕X轴、Y轴、Z轴的夹角分别为α、β、γ，旋转轴的方向可以表示完成一个单位矢量

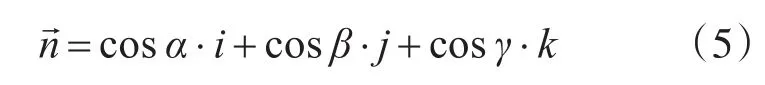
则有固定点刚体通过绕该点的某个轴旋转角度θ到达新姿态，则描述该旋转角度的四元数Q表示为

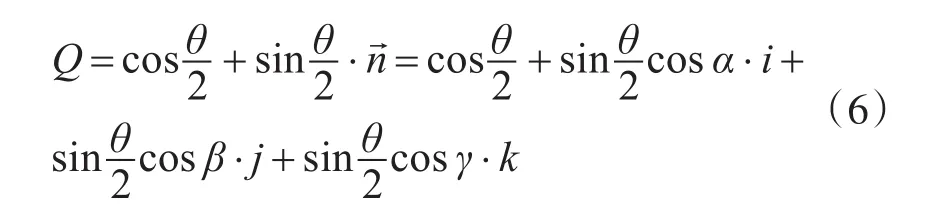
由式（6）得出欧拉角到四元数的转换公式：

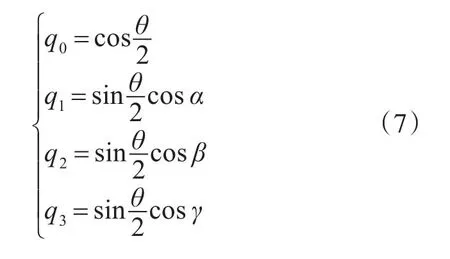
2.3.3 四元数姿态更新方程

惯导数据是定时采样，固定时间间隔输出。为了减少噪声在积分中的影响。系统直接将角增量来确定四元数［10]。

四元数姿态更新方程

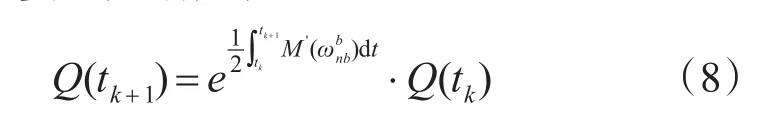
为了降低计算复杂度对式（5）进行展开得到三阶近似算法：

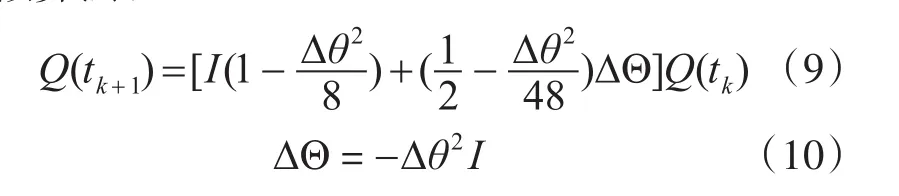
其中I为单位矩阵。

3 基于DSP 28335的惯导解算设计与优化

3.1 基于DSP 28335的程序设计

DSP28335芯片有两个带数据缓冲功能的高速输入输出串口，和一个不带数据缓冲功能的普通串口。本文程序设计只使用其中两个带数据缓冲功能的高速串口：第一个串口用于接收陀螺和加速度计数据；第二个串口用于接收上位机命令数据并且发送惯导解算数据。串口中断程序负责接收串口数据，主程序负责解析串口协议以及执行相应串口命令和解算惯导数据，并控制串口发送数据。

DSP 28335主程序如图2所示，系统启动后首先初始化芯片资源设置看门狗，设置芯片主频，初始化全局变量，初始化GPIO口，初始化串口，初始化系统中断，进入程序循环，判断串口缓存区是否存储串口数据，如果串口缓存区存在数据就进行串口协议解析，当串口数据满足协议时进行相应分析，如果是上位机设置命令则进行相应参数设置，参数设置完毕后发送参数设置应答；如果是来自惯导数据则进行相应串口解算，将解算结果通过串口发送上位机。

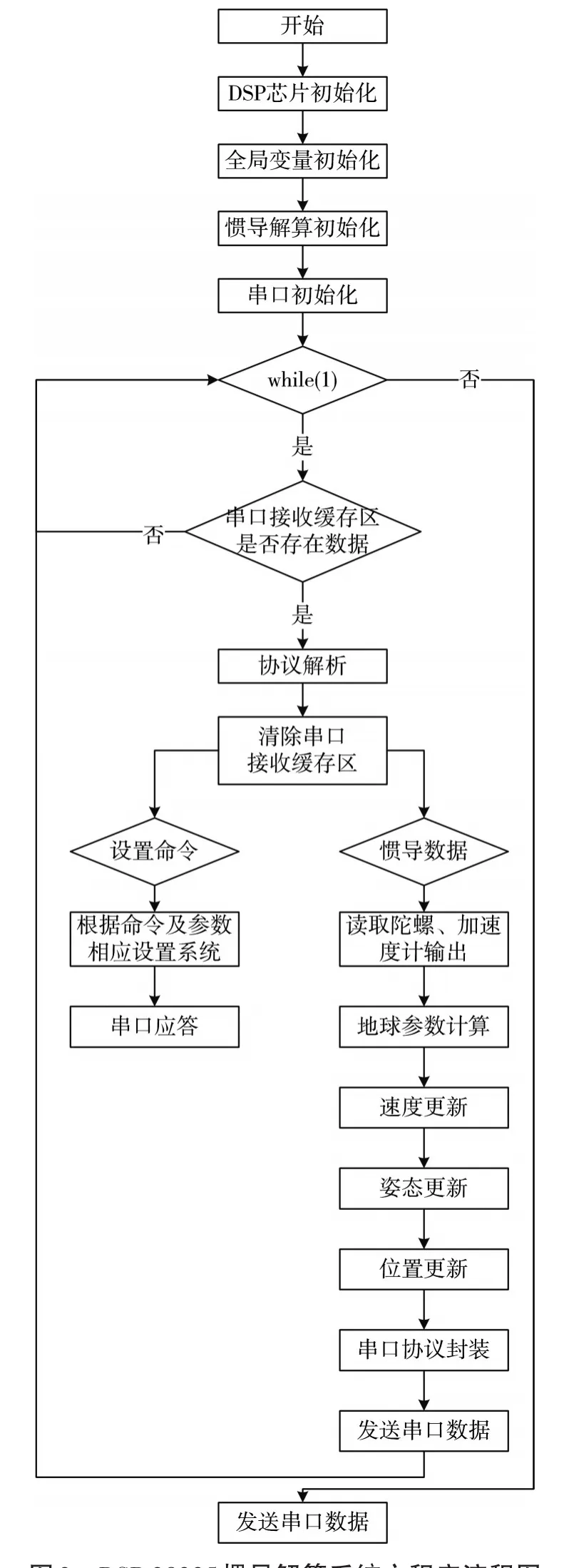
图2 DSP 28335惯导解算系统主程序流程图

当有串口收到数据后DSP芯片会产生中断信号，调用相应中断函数。中断函数流程如图3所示，首先读串口数据，然后将串口数据添加缓存区中，最后清除中断标志，表示串口中断处理完成。

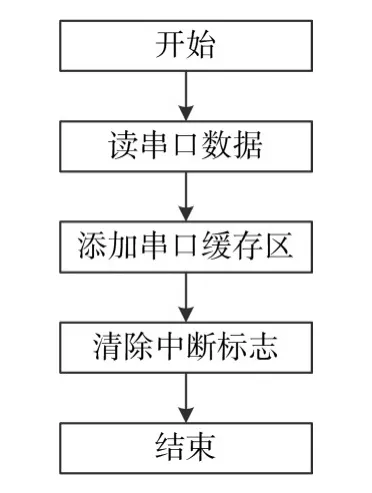
图3 DSP 28335惯导解算系统串口中断函数流程图

3.2 算法优化

通过算法计算原理进行优化，这一步可以极大减少计算量也是最重要的优化手段。先分析计算原理和过程，有目的性减少计算量。例如惯导解算公式（10）

通常做法：

第一步计算Δθ2=Δθ×Δθ；

第二步计算 -Δθ2=-1×Δθ2；

第三步创建单位矩阵I；

第四步将单位矩阵每一个元素和-Δθ2相乘。

优化后：

第一步计算Δθ2=Δθ×Δθ；

第二步计算 -Δθ2=0-Δθ2；

第三步程序初始化定义值为0的矩阵I0纬度和矩阵I一致；

第四步将-Δθ2直接赋值于I0对角线元素。

通常做法计算原理过于呆板导致计算量过大，本文利用DSP系统加减法速度优于乘除法的优势，用 -Δθ2=0-Δθ2代替 -Δθ2=-1×Δθ2降低系统运算时间，并且利用单位矩阵只有对角线元素为1，其余为0的特性以及1乘任何数等于其本身，0乘任何数等于0，直接将-Δθ2赋值于I0矩阵对角线元素免除乘计算。再次降低系统计算量，提升系统性能。

3.3 循环优化

C语言优化过程中最主要的手段是从循环语句着手重点优化，采用高效循环方式，或者减少循环次数，亦可不用循环语句。例如C语言中for循环：

for(表达式1;表达式2;表达式3)

{

语句;

}

进入循环前先执行表达式1，在判断表达式2，如果表达式2位真执行for循环中的语句，如果为假则调出循环。当循环语句执行完后则执行表达式3。

可以看出每执行一次循环语句都要判断一次表达式2和执行一次表达式3。则优化方法就是减小循环语句，如果循环次数较少则不使用循环语句。

例如C语言程序中Bk矩阵为4×4,该矩阵很小可以不使用for循环语句，而是直接执行表达式：

以上语句虽然代码量比虽然较长，但是在进行优化前计算次数为278次，改为优化后的代码计算次数为16次，大大减少计算时间。

3.4 变量优化

C语言编程时在函数中往往会定义比较多的局部变量，每定义一个局部变量CPU调用该函数时就会执行压栈出栈操作。算法中的变量比较多，而在普通PC机的CPU性能十分强大可忽略压栈出栈执行语句的耗时。但DSP芯片主频有限就需要尽可能优化减少不必要的指令。因此将函数中的中间变量全部定义为全局变量，这样又能提升系统性能。

3.5 DSP系统优化

DSP系统对Flash储存区访问速度远远慢于对系统内部RAM（Random Access Memory，RAM）的访问，因此要大大提升DSP运行速度就要在系统启动时将程序从flash区搬移至RAM区运行，这样可以大大减少解算时间，对系统性能提升具有非常重要意义。DSP系统还可以通过编译器编译选项优化，TI公司自带DSP开发环境CCS（Code Composer Studio，CCS）编译器提供编译选项-O3最高等级编译优化，此时编译效率已经接近纯汇编模式，因此没有必要对代码进行汇编语言的优化。

4 试验验证

通过示波器波形分析对比优化前后的程序执行时间，图4未优化Flash运行解算时间，图5优化后Flash运行解算时间，图6优化后RAM运行解算时间。

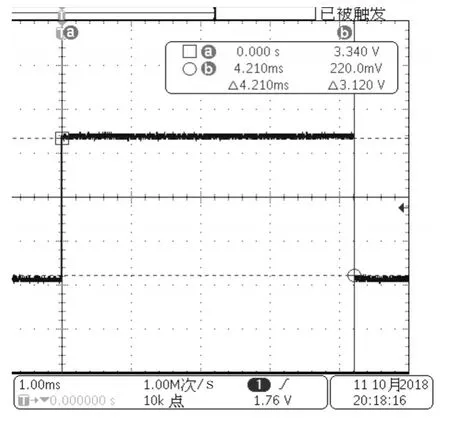
图4 源码未优化Flash运行解算时间

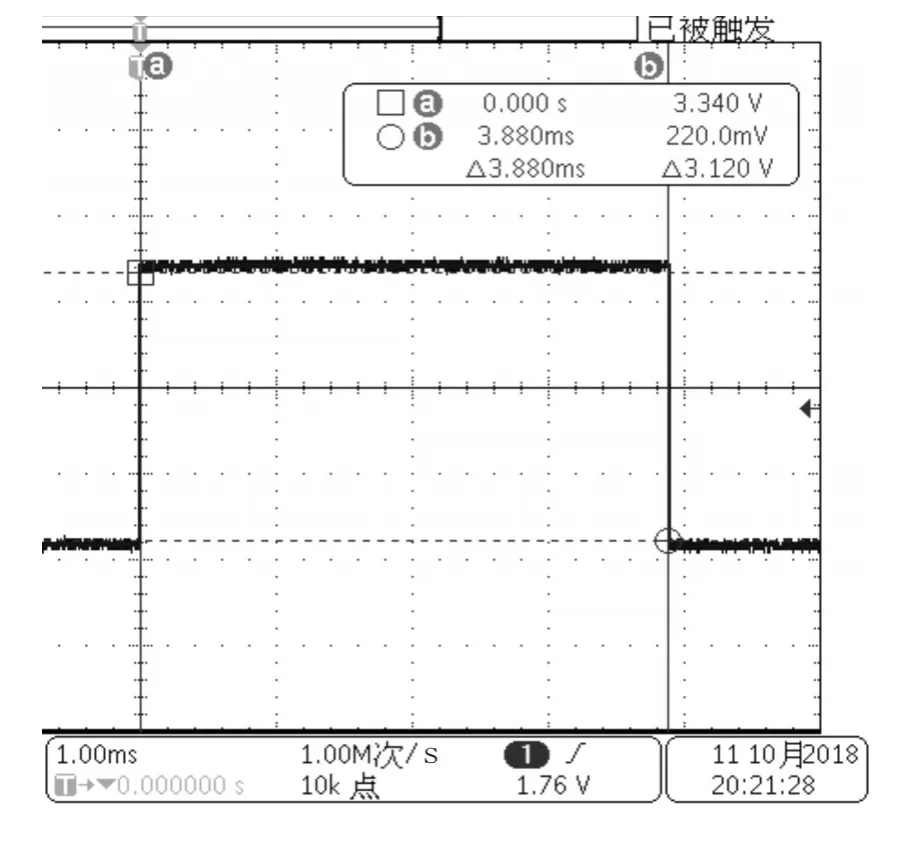
图5 源码优化后Flash运行解算时间

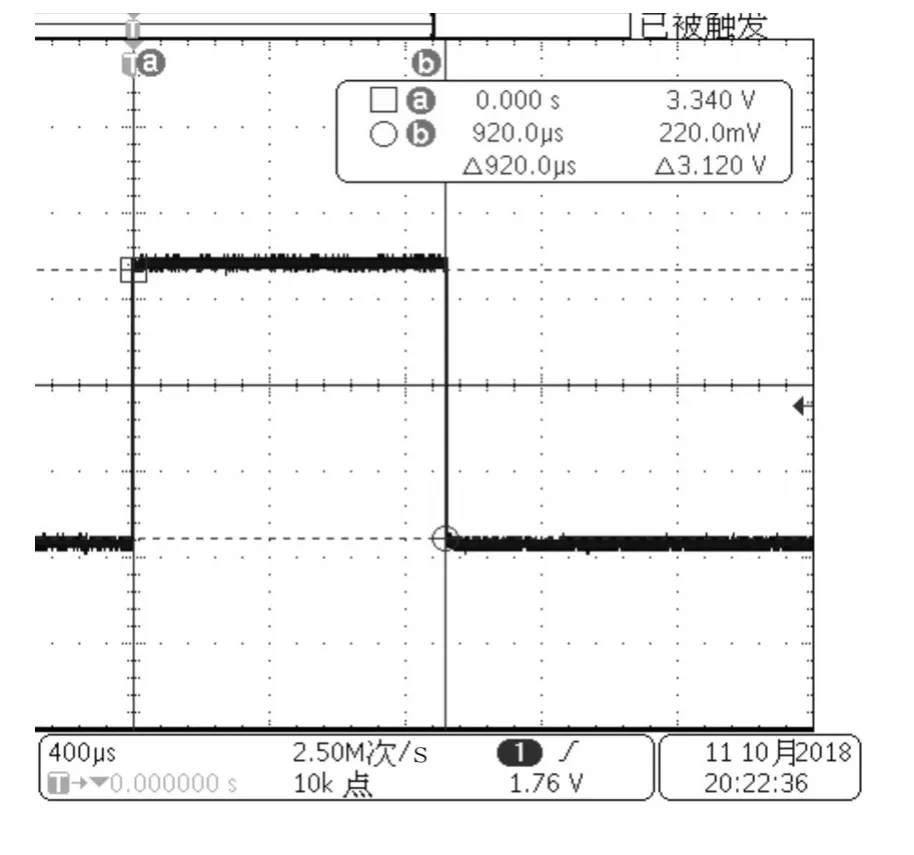
图6 源码优化后RAM允许解算时间

源码未经过优化程序在Flash上运行时惯导解算时间为4.13ms，源码经过优化程序在Flash上运行时惯导解算时间为3.940ms，对比程序优化解算时间减少0.19ms。源码优化后让程序在DSP系统内部RAM上运行解算时间为0.928ms，对比解算时间减少3.012ms。通过整体优化共节约时间3.202ms。

5 结语

本文通过惯导解算程序进行设计优化，针对DSP 28335平台的优化进行详细分析介绍，并通过试验及实测数据验证了优化的有效性。通过程序优化可以使系统运行效率有小幅度提升。试验验证惯导解算时间节约3.940ms，性能提升7.8%。通过对DSP 28335系统优化，将程序搬移至DSP内部RAM区运行惯性导航导解算时间节约2.952ms，性能提升76%，使系统性能满足高频、高速的惯导解算要求，并得出以下结论：通过程序优化对DSP系统性能提升有限；通过对DSP系统优化能够获得较大幅度性能提升。因此DSP系统优化是惯导解算中一种重要的优化方式，程序优化虽然对系统性能提升有限，依然是DSP系统优化中重要方式之一。遇到对系统要求更加严苛的项目，还可以通过其他优化方式提升系统性能。

TI公司DSP芯片种类繁多，但无论系统设计采用哪种芯片想要最大化获得性能输出，就必须对系统进行整体优化，最大可能性地利用芯片提供资源。