函数测试题B 卷参考答案

一、选择题

1.A 2.C 3.A 4.A 5.D 6.C

7.B 8.A 9.D 1 0.A 1 1.A 1 2.C

二、填空题

三、解答题

18.(1)因为幂函数f(x)=x-2m2+m+3(m∈Z)是奇函数,且f(1)＜f(2)。所以-2m2+m+3是正奇数,且m∈Z,所以m=0,f(x)=x3。

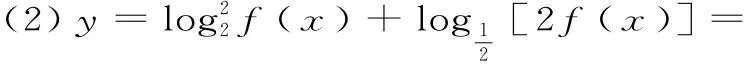
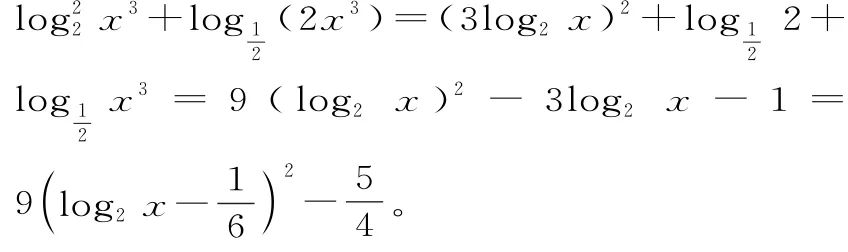
19.(1)二次函数f(x)=-x2+a x-的对称轴为,由f(x)为偶函数,可得a=0。

综上可得,g(a)的最小值为

20.(1)由题意可得(100-x)×2×(1+2x%)≥2×100,化简为x2-5 0x≤0,解得0＜x≤5 0。

21.(1)函数f(x)=ex-x2-1,则又+∞),则

设y=ex-x-1,则y'=ex-1＞0在x∈(0,+∞)上恒成立,即y=ex-x-1在x＞0时单调递增,所以y=ex-x-1＞0。

令g'(x)＞0,可得x＞1,令g'(x)＜0,可得0＜x＜1,所以g(x)的单调增区间为(1,+∞),单调减区间为(0,1)。

所以函数g(x)的极小值为g(1)=e-2,无极大值。

当x＜x0时,h'(x)＜0,h(x)单调递减,当x＞x0时,h'(x)＞0,h(x)单调递增,所以

又h'(x0)=0,则h(x0)=又x0∈ (-1,0),则h(x0)∈,即对任意x∈R恒成立,所以k≤h(x0),由kmax=-1,得出k的最大值为-1。