逐步逼近法计算LED透镜

周士康，杜 金，陈春根

(上海三思电子工程有限公司，上海 201199)

引言

计算LED透镜的形状有多种非成像光学的设计方法[1-5]。其中光通量线(以下称LFR)方法[4]可以计算给定任意照度分布的透镜，而偏折能力分配法[5]则可以同步计算多表面透镜。同时用这两种方法是一个计算透镜的优秀方法，其计算步骤如下：

1) 在极坐标中把LED光强的空间分布曲线分为n份，但各份的光通量必须相等，分割线的方向就是透镜的n条入射线的方向，构成一个n维的入射线角度数列。

2) 因为每条光线光通量相同，像面的照度分布要求可以转换为光线在像面上的分布，从而得到像面上n条光线落点的位置。假定透镜尺度相对很小(远场条件)，得到n个出射线方向。也构成一个n维出射线方向数列。

3) 透镜出射线和入射线的方向之差称为总偏折角，由求得的上述两个序列后可以求得总偏折角序列。设透镜表面数为m，把此n个总偏折角每个都按各面的权重再分到m个透镜的表面上，这就得到了(m+1)×n个角度，也就是得到了每个面前后的入射角和出射角。

4) 用折射定律对每个表面依次计算各得n个小线段连成一条折线，共m条折线，构成透镜的m个表面。当n很大时就是一个平滑的透镜表面。图1为双面LED透镜m=60、n=50的示例。

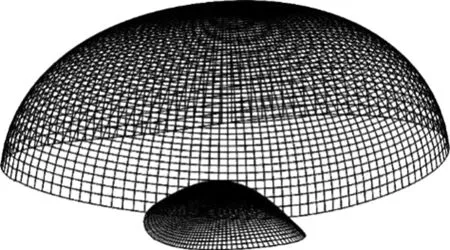
图1 LFR方法计算单透镜

上述LFR方法假定了LED尺度很小，也就是满足远场条件。但如果像面比较近，即LED的尺寸相比照明尺度不是非常小，不能满足远场条件，计算就会有误差。为了解决这一问题，我们提出了用于透镜设计的逐步逼近的方法，本文着重叙述逐步逼近方法的概念，具体的公式和程序不在本文中出现。

1 逐步逼近法

1)动机。上述LFR方法在处理一般问题时都符合“远场”条件，此时透镜上折射点的位置的不同对像方光分布基本无影响，我们只需关心光通量线的方向而不是折射点的位置。但是在“近场”情况下，光线在透镜上的位置会影响照明的结果。近场问题的处理应该用光线在表面上的位置来表征。但这对透镜形状的计算却带来很大的困难。其原因在于折射定律擅长的只是求解介质表面的方向和折射线的方向之间的关系。在许多领域的实际工作中，求解的方程十分复杂或者是无法直接求解时往往可以使用逐次逼近的方法[6]，此法在大量实际问题中都得到了广泛的应用。由此我们想到，如果能把这种逼近法的思想用到LED透镜的计算中，也许可以解决原来解决不了的求解问题。本文的结果说明这是可以做到的。

2)可行性。处理近场问题的困难在于已知LED发出的入射光线的方向和像面的落点无法解得透镜的形状。但如果能够尝试性地给出出射方向就可以解得初始的形状。于是我们提出先给定一个尝试平面作为透镜的最后一面，并给定该面上各光线的尝试折射点，再按照度分布要求给定LFR在像面的落点，这就可以得到出射光线的尝试方向，这样就可以用原有的LFR方法计算得到初始透镜形状。然而再逐步修正透镜使之逐渐满足“落点”的要求。经过多次逼近计算，可以得到符合折射定律和落点要求的透镜形状。本文的结果说明这是可行的方法。

3)难点。这个方法的难点是如何给出下一次逼近的光线方向。对此我们用最为简单的方法很好地解决了这个问题。就是简单地把尝试计算得到的新的折射点到目标落点的方向作为下一次计算的方向。

2 逐步逼近法计算LED透镜的步骤

2.1 计算入射LFR角度序列

考虑一个旋转对称单透镜，平面像面、均匀照度分布、极少的光线(n=8)。此例并非某个实际设计的例子，只是为了形象地说明逼近计算方法而设定的。

设LED位于坐标原点，透镜前表面中心在A点(x=10 mm)，后表面在B点(x=30 mm)，弧形像面中心在C点(x=70 mm)，见图2。

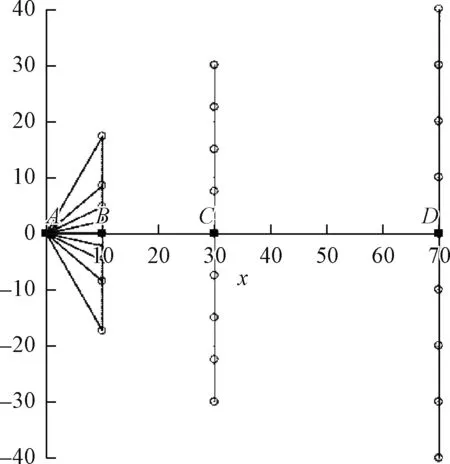
图2 LED的LFR及光线目标落点

按照LRF方法，首先需要求得LED发出的光线的方向序列，这些光线携带相同的能量。由于照度正比于单位面积上的光通量，而光通量正比于光强与立体角的乘积，因此光强分布曲线对总光束角的积分的值将正比于总光通量。根据这一规律，可以把LED发出的光能按照携带的光通量相等而分成8份(以n=8为例)，即把光强分布曲线对总光束角的积分的值分成8等份。它们的角度间隔就是9条具有相同能量的LFR的方向，这便是透镜入射线方向序列。示意性的结果见图2左部原点出发的9条光线簇，大致可以看到这里是大光强处光线密度大，小光强处光线密度小,符合光强空间分布规律。LFR计算的具体方法[4]在此不详述。

2.2 设定像面和光线落点

由于LFR是带有相同能量的光线，因此像面的光线落点的密度分布决定了像面的照度分布，这就不难根据事先给定的照度分布求得LFR的落点沿像面的分布。

在照度均匀分布的情况下，只要将位于D处的被照明平面均匀分成8份即可得到9个落点，得到图2所示的9个小圆形分割点。

对非均匀照度分布时，可以事先给定照度分布函数，再按照落点的密度正比于照度的原则来划分。

2.3 设置尝试平面及尝试折射点

这是逐步逼近法的重点。在透镜的后表面位置C点即x=30处给定一个任意长度例如70 mm的垂线，代表尝试平面直径。在这个垂线上任意给定9个小圆形试探折射点。

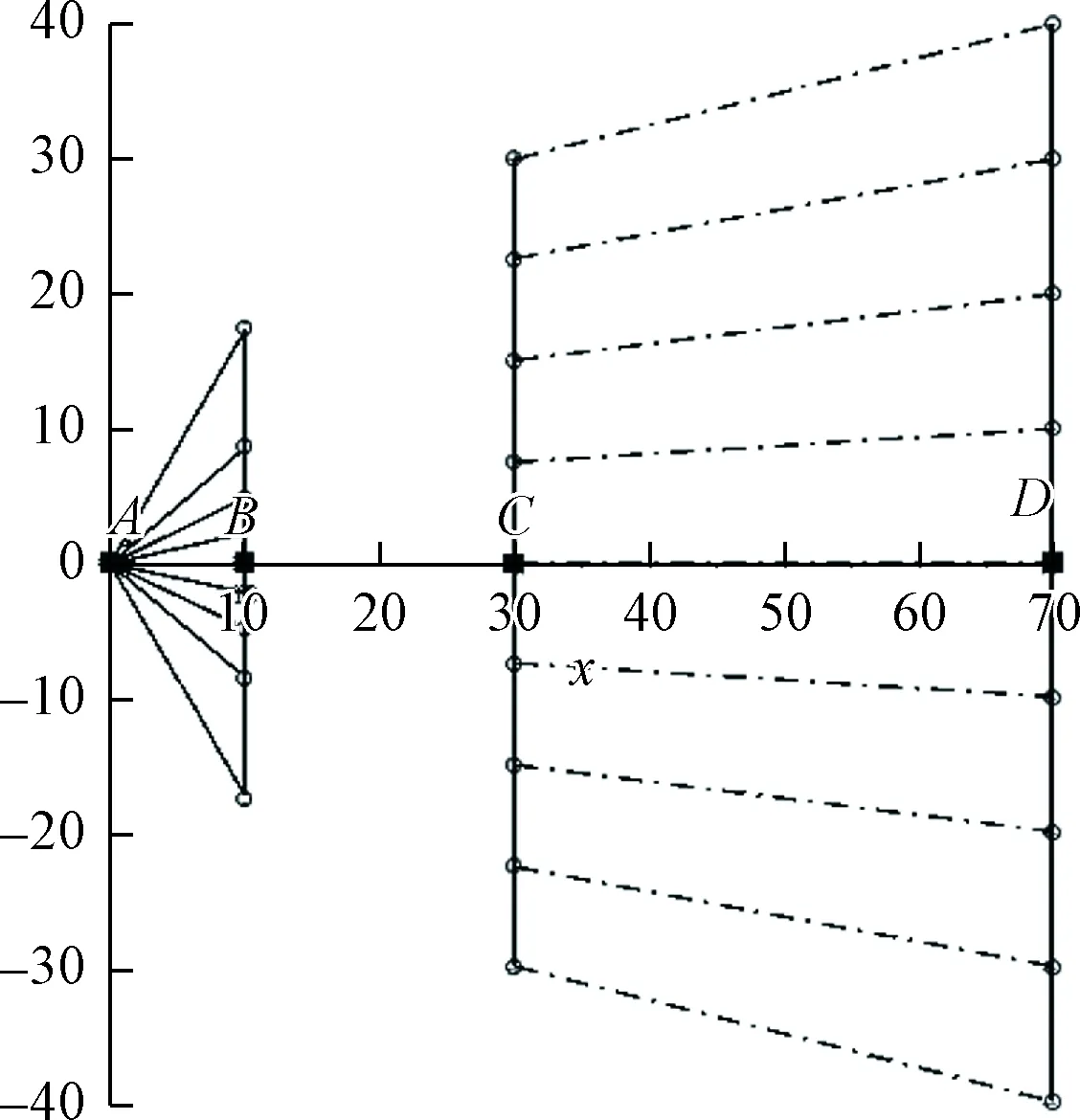
图3 入射和出射的LFR角度序列

把图3中C平面和D平面上的9×2个小圆一一相连，连线(图3中的点划线)的方向代表光线从LED最后一个表面出发方向，构成了透镜出射线方向序列。这样就得到了透镜的入射线和出射线两个尝试角度序列。

有了这两个角度序列，我们就可以用LFR的方法进行计算求得透镜的形状了。对于单透镜的情况，设两面的折射能力相等，则可求得上两个角度的平均值，就得到第三个角度序列，那就是在透镜内部的光线角度序列(图3中没有画出这一个序列)。有了这9×3个方向，我们就可以顺序用折射定律计算得到透镜前后表面共8×2个小面的角度和位置，结果得到了一个弯月形的透镜，见图4的粗实线。

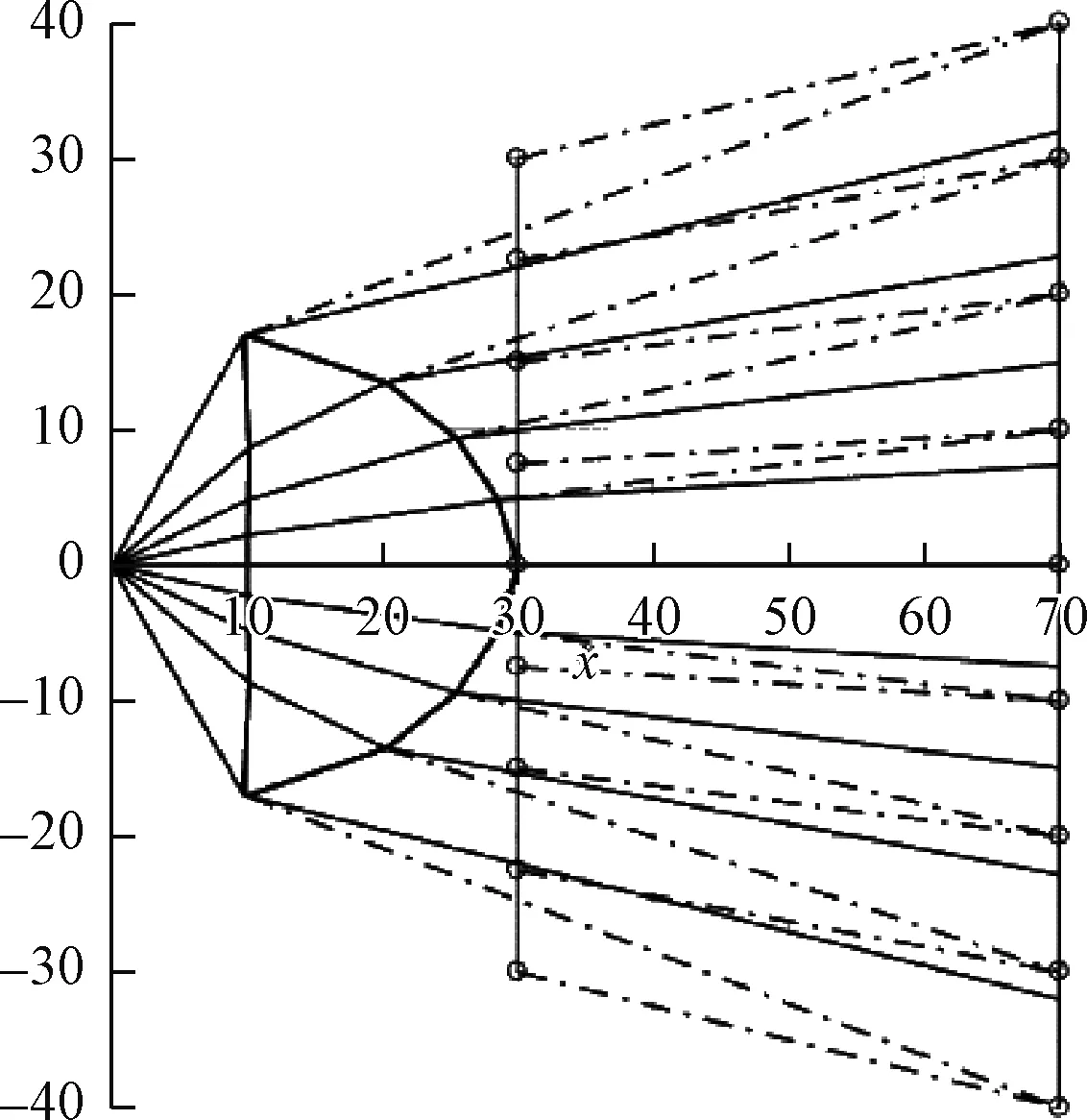
图4 第一次计算结果和修正角度

2.4 逐次逼近法计算透镜形状

可以看到，第一次循环后试探平面自动变成了曲面，从其上的折射点发出的光线(实线)的确和试探方向(点划线)精确平行(这正是LRF方法的结果)，但是却没有射向希望的落点。实际落点与目标落点之差最大达13.6 mm。逐步逼近法可以迅速缩小这一偏差，但如何选择下一次计算的修正量是逼近法成功与否的关键。

我们的解决方法是简单地用第一次计算得到的透镜后表面的光线落点和希望的像面落点(图3中D面的小圆形)的连线(图3中虚线)作为第2次计算的像方光线的方向，进行第2次计算，第2次计算结果如图5所示。这时，实际的光线落点和希望落点之差Δmax=0.14 mm，比第一次的结果缩小了约100倍。

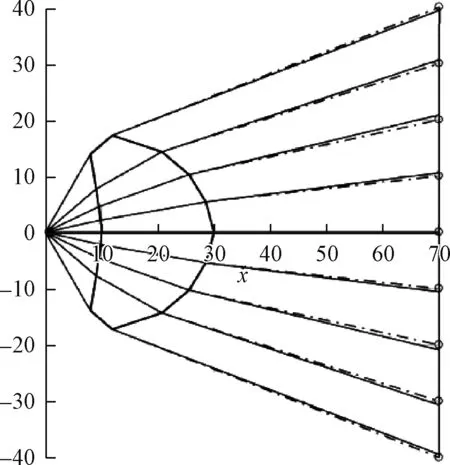
图5 第二次计算结果

继续上述计算，在本例中经过4次逼近计算后就得到了理想的结果，如图6所示，最大误差仅为Δmax= 0.003 mm。

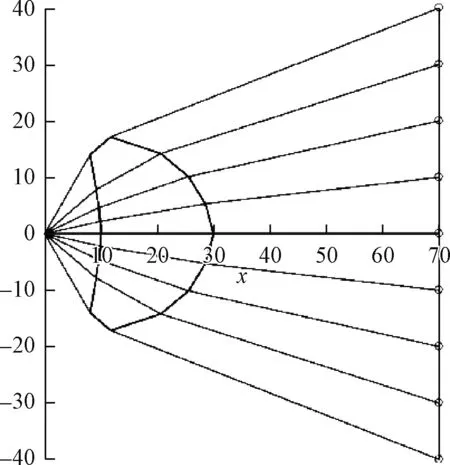
图6 最终结果

增加LFR的数目，如n=40，5次循环后的结果如图7所示。这时Δmax=0.005 mm，曲线也较为平滑了。实际设计中一般n的值为200左右就可以得到可以用于加工的平滑的表面。

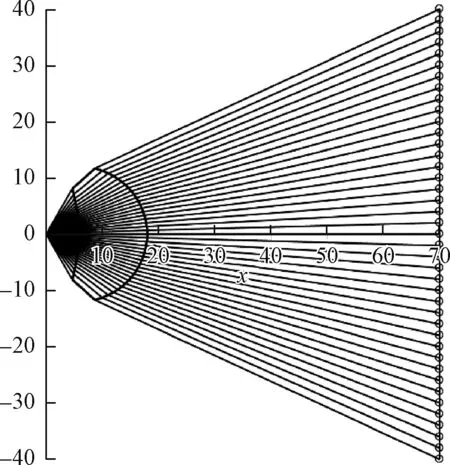
图7 n=40时的计算结果

以上用直观的图形较清晰地给出了本方法的内容，方法中完全不涉及复杂的微分方程等计算，这就不难编写计算机程序。

实践表明，试探面的形状、大小和其上的落点的位置分布的宽容度很大，即使初始给出的是一个非平面的尝试表面和非均匀的尝试点分布，用逐步逼近法都将趋向于同一个结果。

3 非均匀照明的逼近法设计

以上的例子是均匀照度分布。对于非均匀照度分布，只要给出像面照度分布函数也可以进行计算。例如，给定一个中心照度小而边缘照度大的正弦函数分布a+b·sin(x+c),其中a=31、b=30、c=-90°，其照度分布函数如图8所示。

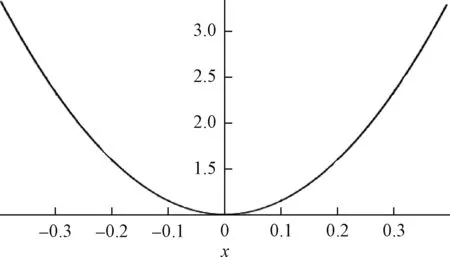
图8 正弦函数给定为像面照度分布

计算得其透镜形状和LFR分布为图9所示。其光线落点的密度沿弧面的分布是按图8的正弦分布由中心向边缘变大。

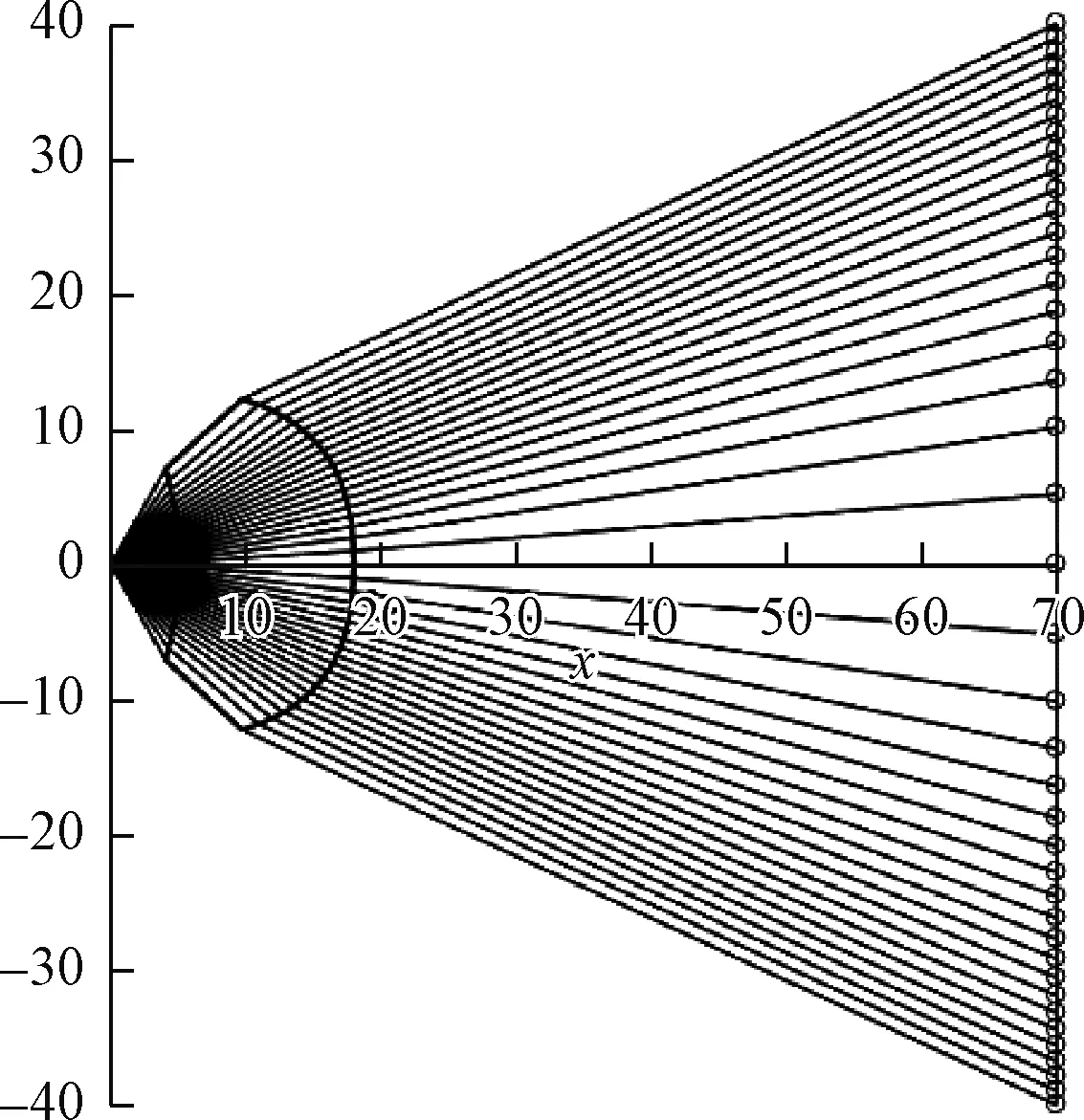
图9 按照事先给定照度分布的计算结果

对于其他类型的照度分布，只要给出分布函数，可以套用上面的方法。好在实际的工程中都不需要用复杂的照度分布，因此给出函数也不是难事。

4 被照面为非平面的逼近法设计

考虑到在近距离照明中有时会遇到像面不是平面的情况，用平面代替弧面必然会带来误差，而用我们的逼近方法计算却可以容易地处理非平面像面的问题。

被照明面是一个曲面并没有给我们的计算带来任何困难。只要在这个曲面上按照照度分布的要求求得一个个光线的落点的坐标就可以了。唯一的困难是在数学上描述这个曲面，实际工作中这也不是难事。

以下用一个球表面均匀照度分布为例。假定其圆弧可以用下列参数方程表示：

x(x0,R,t)=x0+R·cos(t)，y(y0,R,t)=y0+R·sin(t)

其中圆心的坐标为(x0,y0)，R为半径，t为辐角。

在本例中，被照明面是中心在C点(x=70 mm)，半径为130 mm的凸弧形表面，圆心在x=200 mm，y=0。

将此弧面均分42份，得到图 10所示的43个分割点。若希望非均匀照度分布，则需要按照落点密度正比于照度的原则求得落点位置。

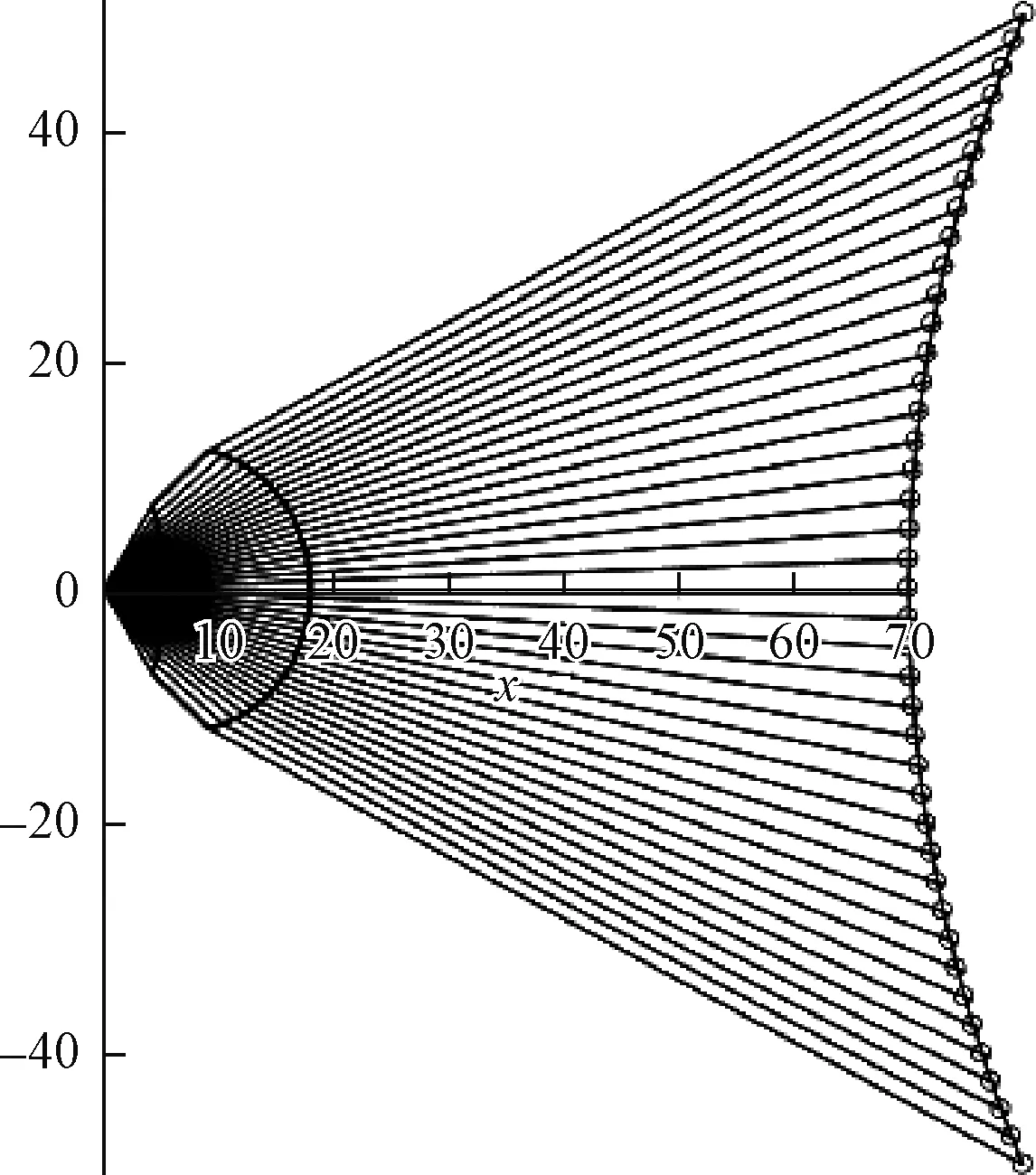
图10 非平面的被照明面

对一个可以用参数方程表示的二次曲面，逼近方法同上。其他形状也是用参数方程表示方便。

5 多透镜的逼近法设计

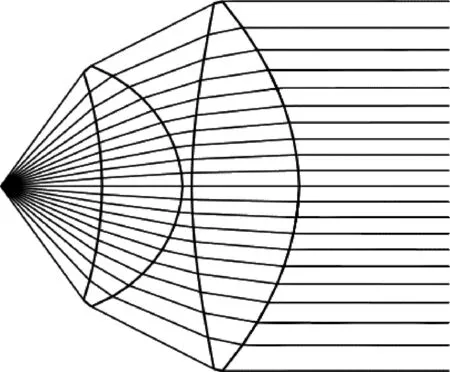
图11 LFR方法计算双透镜

LRF方法中计算多个透镜的方法同样可以用在本方法中。某些LED透镜若做成双透镜会比单透镜更为合适[5]。SSWYD-800型无影灯[7]有一款透镜就做成了双透镜。其光线较少时的计算结果见图11。为了显示清楚些，图形用了n=20的计算结果。图11为无影灯的工作距离为1 000 mm时，用文献[7]的总体设计方法，用逐步逼近法同步计算的LED无影灯的双透镜四个面的计算结果。我们也用文献[4]的方法按远场条件进行了计算，得到结果一致，这是因为此时满足远场条件了。

6 结论

我们用逼近法计算LED自由曲面透镜，从建立一个虚拟的尝试表面并给定尝试点出发，给出了修正计算的方法，进行多次循环计算，避开了求解方程等复杂的问题，不但可以得到很高的计算精度，还具有快速的收敛速度。

从计算的角度看，本文的方法实际上解决了一个从“方向”转为计算“落点”的问题，以前是由计算光线方向来求透镜形状[4，5]，而现在近场问题则是要由计算光线落点来求透镜形状。

逼近法把计算透镜的LFR方法扩展到既可以用于近场计算，又可以用于远场计算，既可以计算平面像面又可以计算非平面像面。同时逼近法保留了原方法的几个重要的优点，如可以用于非均匀的照度分布或事先给定的任意像面照度分布的计算，以及同步计算双透镜系统。这给LED透镜二次光学设计带来了方便。

7 讨论

1)设想被照明面位于x=1 000 m远处，则其上1 mm的落点位置误差其角度差别只有0.0001°，可以让程序使用12位有效数字，角度精度可以非常高，则即使多次运算也不会带来有影响的误差。图11说明本方法在非近场的情况同样适用。

2)新方法的必要条件还在于这种逼近能否收敛。实际工作证明此法可以收敛，而且收敛速度快，我们计算的多个例子都是循环次数在10以下时计算误差小于0.001 mm。

3)逐步逼近方法可以推广到其他难以一次性直接计算的问题中去，如一个面既有反射又有透射的LED照明系统[8，9]。此时，一般方法难以求解得到曲面的形状，但逼近法可以计算得到。