纱线波谱图机理及实例分析
2019-09-25王学元
王学元
(中国纱线网,杭州 311203)
纱线波谱图是条干仪将纱线的质量波动通过系列分析计算后,转换成频谱图形成的,这个分析计算过程被称作傅里叶分析。傅里叶理论认为,任何周期性的函数都可以分解成系列正弦波的叠加。因此,通过傅里叶分析,纱线上任何周期性疵点都可以简化成系列正弦波的频谱,直观地展现在波谱图上。
1 纱线波谱图的形成机理
笔者以连杆机构的方式演示周期性函数分解成正弦波叠加的原理。
1.1 正弦波
为便于对正弦波形成过程的理解,假设有1个两连杆机构OPE,O点为固定点,P为连接点,E点为端点,P点绕O点按逆时针以角速度ω转动,让E点在一张以与P点等线速直线运动的白纸上画线,就可以得到1个正弦波波形,那么这个正弦波包络曲线内的面积一定与圆的面积相等,见图1。
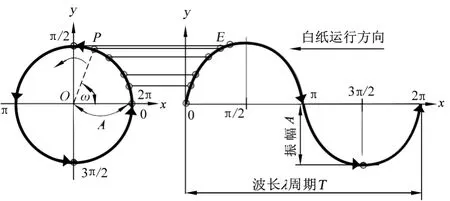
图1 正弦波形成示意
纱线生产过程中,有圆周运动的器材专件,如果出现弯曲、偏心等问题,会造成纱条粗细不匀,并以正弦特性规律变化,那么条干测试仪就会通过对其特征进行计算分析,并在波谱图上展现出来。
1.2 非正弦波
罗拉粘花、胶辊损伤、胶圈破洞、齿轮缺齿等会形成周期性非正弦形态的疵点,条干测试仪通过傅里叶分解后会将其简化成系列正弦波的叠加,笔者以矩形波为例简要说明。
在两连杆机构连接1根连杆PD,令PD绕连接点P以角速度3ω运行(即在原来正弦波的基础上叠加其3次谐波),则E点的运行轨迹如图2所示。
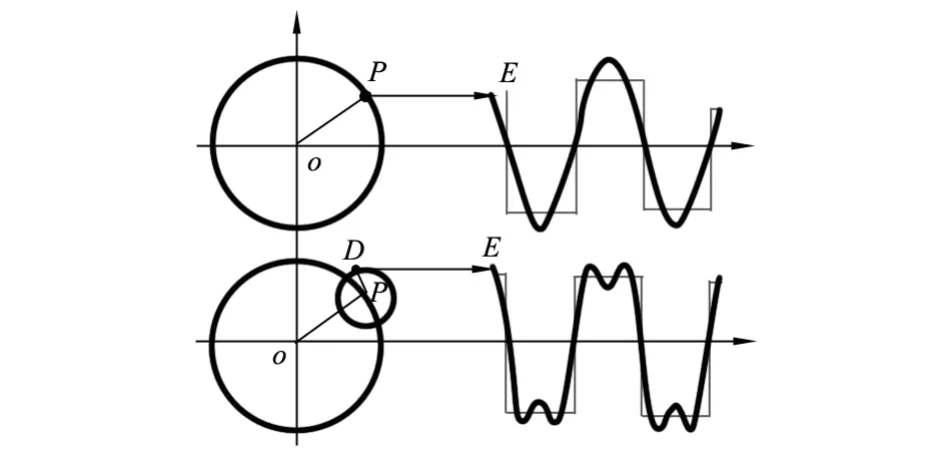
图2 正弦波叠加3次谐波
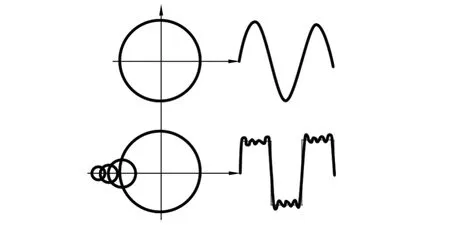
图3 正弦波叠加3次、5次、7次谐波
用同方法在原来正弦波的基础上叠加3次、5次、7次谐波后,就会形成如图3所示的轨迹。如此不断叠加其奇次谐波,最终会叠加成一个标准的矩形波,也就是说,1个矩形波可以分解成1个正弦波与其奇次谐波的叠加。
如果在1个正弦波的基础上,同方法叠加2次、3次、4次谐波,就会形成一个近似三角形波。如此不断叠加其偶次谐波和奇次谐波,最终会叠加成一个标准的三角形波。因此,1个三角形波可以分解成1个正弦波与其奇次谐波和偶次谐波的叠加。
按照这种思路,可将复杂的波形分解成简单的正弦波的组合。任何非正弦的周期性波形经过傅里叶分解后,得到的所有正弦波的包络曲线内的面积之和(即多连杆机构端点运行轨迹所包围的面积),与非正弦波包络曲线内的面积必然是相等的。也就是说非正弦波纱疵经傅里叶分解转变成系列正弦波后,通过频谱的形式体现出来,但并不影响对纱疵大小的度量和判断,甚至通过主波及其谐波的相应关系,还可以更方便地判断出纱疵的形态特点。
1.3 波谱图的形成
1个矩形波可以分解成1个正弦波与其奇次谐波的叠加,设想将这些被分解出来的正弦波依次在三维空间中展开,就会得到不同含义的投影图,俯视图可以得到每个正弦波的相位,左视图可以得到包含振幅大小的频域图像(见图4),这个频域图像就是条干仪获得纱线波谱图的理论基础[1]。波谱图的纵坐标表示纱条不匀的相对振幅,横坐标表示纱条不匀的波长。
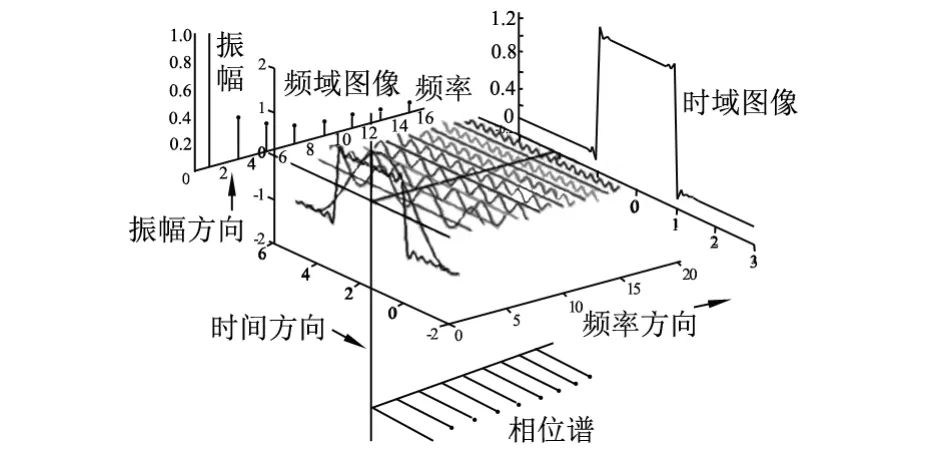
图4 矩形波三维不同方位的视图
2 根据谐波类型判断疵点类型
在条干仪中,波长表示的是周期性疵点重复出现的距离,频率f与波长λ的关系为f=v/λ(v为纱线试验速度)。由于波谱仪中每个频道的频率都是固定的,因此在一定的试验速度下,一旦出现正弦波疵点,波谱仪就会在相应的频道上形成一个凸起的“烟囱”,如果出现的周期性疵点是非正弦波类型,波谱仪就会通过傅里叶分解方法,将其转化成系列的正弦波,然后在相应的频道上形成凸起的“烟囱”。
假设主波以角速度ω运行,那么,各次谐波分别以角速度2ω,3ω,4ω,5ω,6ω,7ω,…,nω(n为自然数)运行。经计算,当主波分别运行到0,π/2,π,3π/2,2π等相位时,其各次谐波的相位见表1。
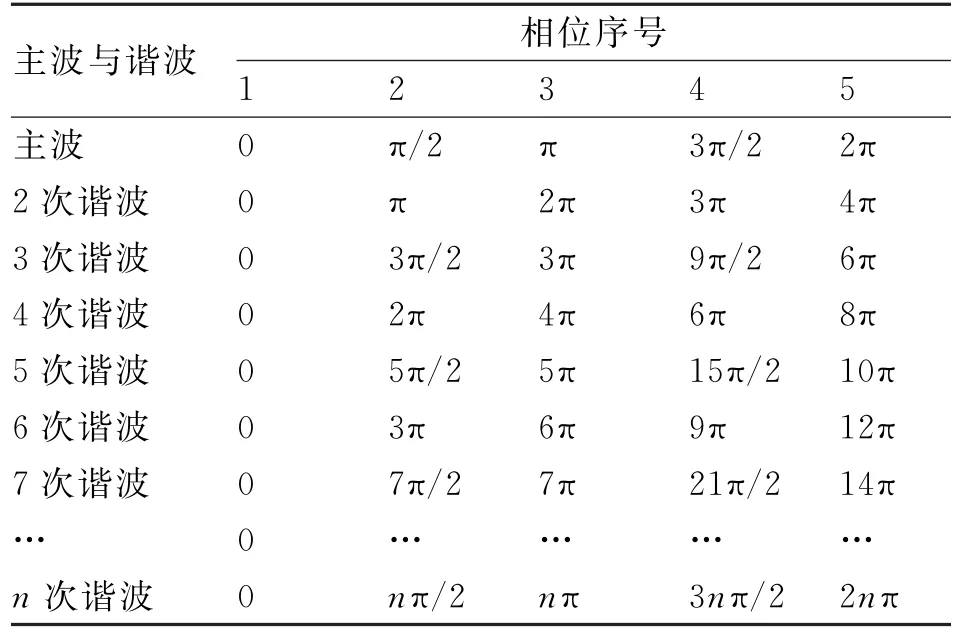
表1 非正弦波的各次谐波与主波的相位关系
从表1可以看出,偶次谐波与主波的相位差为π/2的整数倍,而奇次谐波与主波的相位差为π的整数倍,也就是说,如果主波和谐波同时从0位开始运行,当主波运行π个相位后,偶次谐波的相位不会与主波相位重合,而奇次谐波的相位却会与主波相位重合。
因此,在分析波谱图时,可以借助主波在波谱图上表现出来的形态,研判纱线疵点的形态特征。如对称性的周期性疵点(波形对称于纵坐标的偶函数,如矩形波),只出现奇数谐波而无偶次谐波;非对称性周期性疵点同时出现奇数和偶数高次谐波。
以上分析可知,对称性非正弦波的疵点经傅里叶分解后,不可能具有偶次谐波。因此,如果波谱图有系列谐波,且不存在偶次谐波,那么纱疵就肯定是对称性的非正弦波疵点。而非对称性波形的疵点经傅里叶分解后,谐波必然既有偶次谐波,又有奇次谐波。因此,如果波谱图有系列谐波,且存在偶次谐波和奇次谐波,那么纱疵就肯定是非对称性的疵点。
3 根据谐波的包迹线形态判断疵点形态特点
对于形态类别相同的疵点而言,如果疵点出现的频率不同,分解出的正弦波形态也不同;而形态类型相同的疵点即使出现的频率相同,只要疵点的形态(长度、粗度)不同,分解出的谐波形态(各次谐波的振幅、谐波振幅与主波振幅的比例关系等)也不同。因此,可以根据波谱图的特点分析和判断纱线疵点的特征,作为寻找纺纱设备或纺纱工艺不良的有效手段。
以矩形波为例:假设有1个振幅为A m、脉冲宽度为τ、重复周期为T的矩形机械波,见图5。

图5 周期性矩形波
那么,其傅里叶级数为:
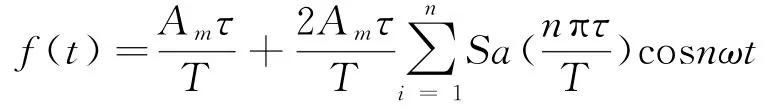
该机械波经过傅里叶分解的n振幅次谐波的振幅为:

这种机械波在波谱图上会出现主波及其奇数次谐波,主波及各次谐波的振幅、波长等与疵点的粗细程度A m、疵点间距T以及疵点长度τ有关。主波及各次谐波振幅大小正比于疵点粗细程度A m及疵点长度τ,反比于疵点间距T。因此,在疵点长度τ不变的情况下,疵点间距T越大,各次谐波的振幅a n越小。当疵点间距T不变的情况下,疵点粗细程度A m及疵点长度τ越大,各次谐波的振幅a n越大。从傅里叶级数展开式中可以看出各种波形图包含的谐波类型及谐波与主波振幅的比例关系。如锯齿波既有偶次谐波,也有奇次谐波,谐波的振幅以1/n的规律收敛;对称性三角波只有奇次谐波,谐波的振幅以1/n2的规律收敛。
4 频道的波长
在条干仪中,每个频道的频率是由固装于仪器内部的数据采集系统决定的,因此各频道的频率f固定不变,第一个频道的频率值为297.742 Hz,相邻两个频道之间按等比进行递减,递减比例为2的1/5次方(普通波谱图),即相邻两频道的频率差异约为15%。每个频道表示的波长由检测时须条的运行线速度决定,因此,其存在关系为:λ=v/f。其中:λ为波长/m,f为频率/Hz,v为须条的测试速度/(m·s-1)。由此数据关系计算出常用测试速度下,各频道所代表的频道中心波长值[2],见表2。
5 谐波的确认和谐波标尺的制作
在波谱图上,有时候会有好几个凸起的“烟囱”,这时就要确认每个“烟囱”是单独的机械波,还是某个机械波的谐波。谐波与主波位置的对应关系与横坐标标尺数字的关系是相互对应的。
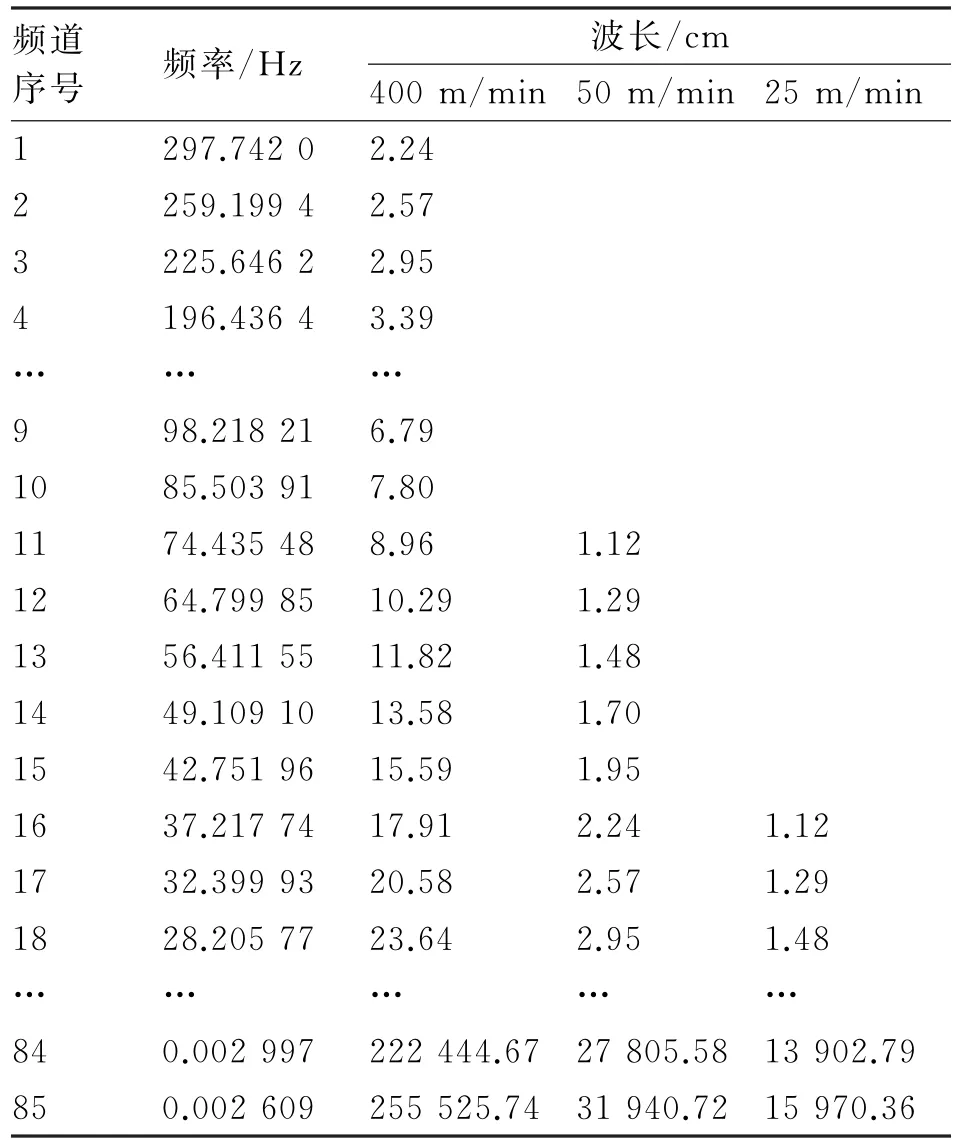
表2 常用测试速度下各频道所代表的频道中心波长值
5.1 测量法
a) 根据条干仪型号打印相应波谱图,依次测量波谱图横坐标1 cm到2 cm,3 cm,4 cm,5 cm,…的距离(或1 m到2 m,3 m,4 m,5 m,…的距离),并分别记录下相对应的第1组数值。
b) 当波谱图上出现较多“烟囱”时,分别测量最右边的“烟囱”到其它“烟囱”的距离,并记录下对应的第2组数据;然后分别测量右边第2个“烟囱”到其它“烟囱”的距离,并记录下对应的第3组数据;直到测完最后一组数据。
c) 对照各组数据与第1组数据系列是否有相同情况,如果某些数值相同,应该考虑这两个“烟囱”之间是否存在主波与谐波的关系。如果某些“烟囱”到最右边“烟囱”的距离分别与1 cm到3 cm,5 cm,7 cm,…的距离是相同的,那么这些“烟囱”很可能分别是最右边“烟囱”的3次、5次、7次谐波。如果各组数据都未与第1组的数据相同,说明这些“烟囱”是独立的机械波,不存在谐波。
5.2 数频道法
普通波谱图上相邻两个频道之间代表的波长是按2的1/5次方等比递减的,即波长相差1倍的两个频道之间,被安排了5个频道。而精细波谱图频道个数是普通波谱图频道个数的2倍或4倍,但波谱分析范围的总长度不变,这说明波长相差1倍的两个频道之间,被安排了10个或20个频道(在特定仪器打印的波谱图上安排的具体的频道个数,可以通过点查20 cm到40 cm、50 cm到1 m、1 m到2 m等合适的位置之间的频道个数确定)。
5.2.1 频道个数的计算
以波长相差1倍的两个频道之间被安排5个频道的波谱图为例,谐波到主波之间的频道个数与它是几次谐波成正比,它们之间的关系式为:5log2n,式中的n为谐波次数。
根据这个关系式,可以计算出各次谐波到主波之间的频道个数,见表3。

表3 各次谐波到主波之间的频道个数
由表3可知,随着谐波次数的增加,相邻谐波之间的频道个数逐渐减少,直至并列在一起。对于安排5个频道的波谱图而言,5次谐波之后各次谐波的频道将会并列在一起。例如:当第60个频道出现主波的波长为7984.03 cm时,计算各谐波的波长及其在波谱图上出现的频道序号,见表4。
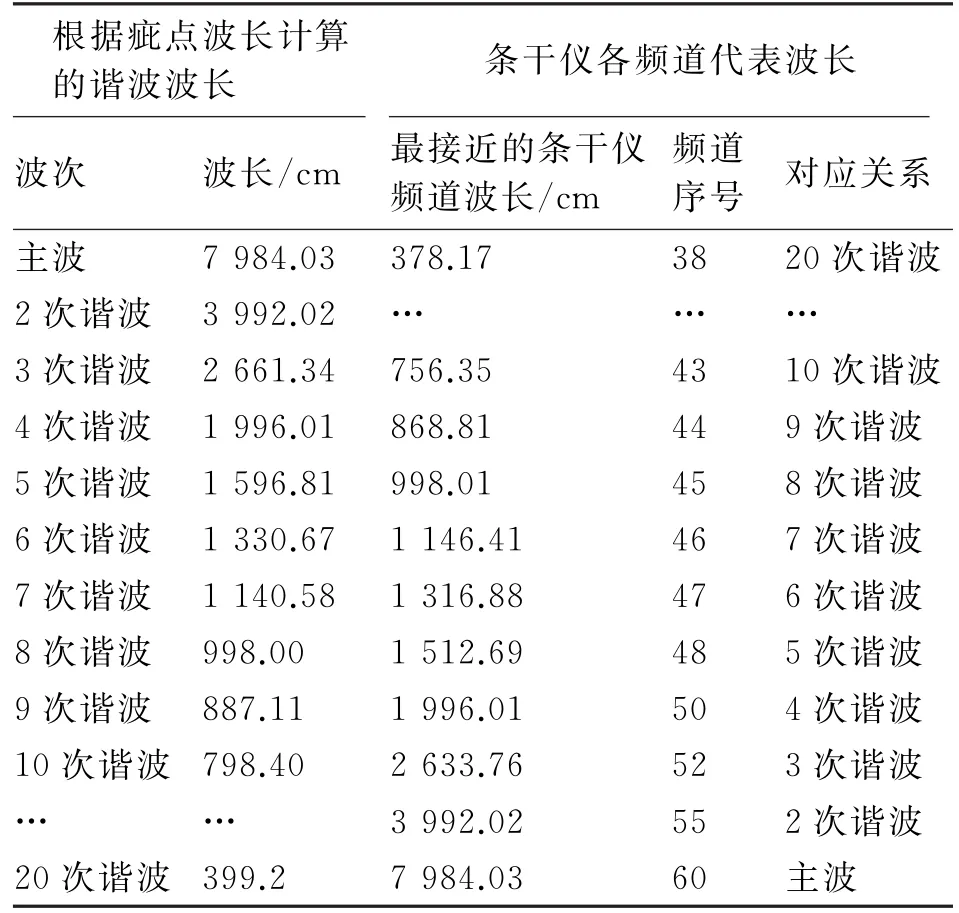
表4 谐波位置出现在频道上的序号对照
从表4可以看出,第60个频道主波的5次谐波在第48个频道上,6次谐波在第47个频道上,5次谐波以后的高次谐波都集聚在一起,这就是波谱图上出现“谐波集聚”的原因,也是某些条干仪配置精细波谱图,在波长相差1倍的2个频道之间安排10个或20个频道的原因之一,因为在单位长度上安排的频道个数越多,越容易区分高次谐波的精确位置。
波长相差1倍的两个频道之间安排10个或20个频道的波谱图,各个谐波与主波之间频道个数的关系式分别为:10log2n、20log2n,计算结果略。
5.2.2 数频道法的使用
根据波谱图的上述特点,我们也可以采用数频道的方法确认某个“烟囱”是不是谐波。
a) 根据所使用的条干仪型号,打印一份相对应的波谱图,查看波谱图横坐标上每单位长度上(如10 cm~20 cm或1 m~2 m等)被安排了几个频道(一般普通波谱图安排5个;精细波谱图显示的频道较多,会安排10个或20个)。
b) 当波谱图上出现较多的“烟囱”时,分别数出最右边的“烟囱”到其它各“烟囱”之间的频道个数,并记录下一组数据。然后分别数出右边第2个“烟囱”到其它各“烟囱”之间的频道个数,并记录下另一组数据,直到测完最后一组数据。
c) 观察各组数据是否符合表3或表4的计算结果,如果某些“烟囱”符合上述计算结果,就应该考虑这两个“烟囱”之间是否存在主波与谐波的关系。
5.3 自制谐波标尺法
5.3.1 谐波标尺的制作
一个个测量“烟囱”间距或点数频道个数,操作比较麻烦,特别是频道较多的波谱图,测量点数容易出错。为方便操作,可以自制谐波标尺。
a) 根据条干仪型号,打印相应波谱图,依次测量波谱图横坐标1 cm到2 cm,3 cm,4 cm,5 cm,…的距离(或1 m到2 m,3 m,4 m,5 m,…的距离),并分别记录下相对应的数值。
b) 做一块宽度合适的透明塑料薄板,在其右端刻画出一个起点,标记为1,从这个点开始依次往左,测量出第一步记录下的1 cm到2 cm,3 cm,4 cm,5 cm,…的距离,并分别刻画出标记,依次标记为2,3,4,5,…,制作好的谐波标尺刻度与波谱图的横坐标方向正好相反。
5.3.2 谐波标尺的使用方法
a) 当波谱图上出现较多的“烟囱”时,将谐波标尺的刻度1对准波谱图上最右侧的“烟囱”,如果其左侧的“烟囱”正好对着谐波标尺上的某个刻度,则这个“烟囱”就有可能是最右侧“烟囱”的谐波。图6中,左侧的3个“烟囱”分别对着标尺的2,3,4,那么它们可能就是最右侧这个“烟囱”的2次谐波、3次谐波和4次谐波。
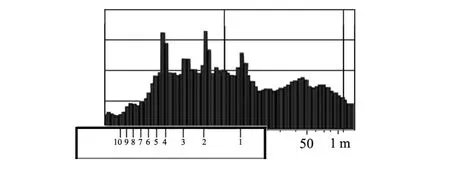
图6 谐波标尺的使用方法
b) 经检查,如果最右侧这个“烟囱”没有谐波,还可以继续将谐波标尺往左侧移动,依次检查其它“烟囱”有无谐波。
5.4 谐波验证需要注意的事项
波谱图单独使用时也存在缺陷,使用不当也容易造成误导,因此,在用波谱图分析纱线质量问题时,还须注意以下几个方面。
a) 非周期性的疵点无法在波谱图上直观显示。如果纱线疵点不是以周期性或近似周期性的形态出现,即使纱线疵点很多、条干很差,也不会在波谱图上直观地显示。因此,经常会发现某些管纱的波谱图看起来很正常,但条干值却很差,这很有可能就是因为纱线上存在着非周期性疵点的原因。
b) 周期性疵点是否连续性出现无法直观地显现。由于波谱图只显示了周期性疵点的波长和相对振幅,因此,只要疵点在检测长度内出现的次数达到某一规定数值,不论它是连续性出现、间隙性出现,还是只在某段内出现,都会在波谱图对应的频道上显示出同样的图形。
c) 周期性疵点的相位无法直观地显现。某些机械缺陷会造成粗节和细节相伴出现,但缺陷的部位和性质不同,有时粗节和细节出现的先后顺序也不同,但只要粗节、细节的形态(长度、粗细程度)相同,那么波谱图上显示的图形都是一样的。
d) 疵点形态的具体细节无法直观显现。有时候一个波谱图上有多个“烟囱”或“山包形”凸起,那么这些波是各自独立的疵点,还是有主波与谐波的关联性关系?单从波谱图上无法准确辨别,还需要其它信息辅助确认。
e) 波长不断变化的非一致性疵点,在波谱图上无法体现出变化的具体情况。有时候,在须条上会有多个波长的周期性疵点,条干仪经傅里叶分解后,在波谱图上会将每个波长在相应的频道上显示,但每个波长在须条上的具体分布状态却无法准确地表示出来。如图7所示的3种波形,虽然在须条上的状态差异十分明显,但其所包含的4个疵点的波长和振幅确实都相同,因此表现到波谱上的图形是相同的。
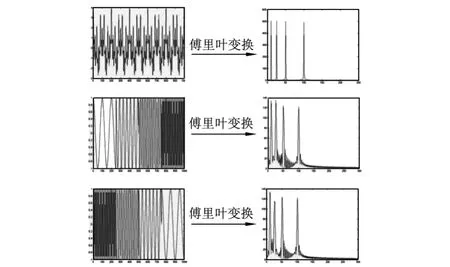
图7 不同疵点在波谱图显示相同的状态
因此,为了提高纱疵分析的准确性,必须使用曲线图、DR图、长度—变异曲线等工具辅助分析。
6 几种非正弦周期性疵点波谱图实例分析
在纱线波谱图上,由机械问题造成最常见的疵点类型主要有:正弦波、三角波、锯齿波、单向脉冲波和正负脉冲波等。
6.1 正弦波形态的疵点
在纺纱设备上,如果某个做圆周运转的部件出现了偏心和弯曲等问题,会造成须条呈现出正弦波动状态的粗细不匀。此类疵点在波谱图上表现为一个独立的机械波,其波长与故障部件的周长成倍数关系。
6.2 非正弦性质的周期性疵点
非正弦性质的周期性疵点可分为对称性和非对称性两类,其谐波排列状态、谐波振幅的包迹线(指同一机械波形成的主波及各次谐波顶点的连线)形状取决于周期性不匀的波形特点。
6.2.1 对称性非正弦波周期性疵点
对称性非正弦波周期性疵点的常见类型有矩形波疵点和三角波疵点等,其在波谱图上会出现主波及奇次谐波。在实际纺纱工艺流程中,出现完全对称性非正弦波周期性疵点的机会较少,但在特定的情况下,也有可能会形成这种疵点。
6.2.1.1 案 例 一
某企业的技术人员在试验中发现一管纱的波形异常,在15 cm~18 cm,5 cm~6 cm和3 cm~4 cm处分别有一个双柱波。经上机检查发现,该锭位的绒辊轴弯曲绕花,绒辊在转动过程中的线速度出现周期性变化,造成绒辊上吸附的短绒也逐渐出现厚薄变化,这两个因素叠加后造成绒辊每转动一周,前胶辊受到的摩擦阻力形成一个类似三角波的周期性变化。该绒辊直径为50 mm,其产生疵点的波长为5 cm×3.14=15.7 cm,与波谱图上机械波的波长吻合。将绒辊换掉后重新纺纱试验,波谱图恢复正常,确认该疵点是由于绒辊轴弯曲绕花造成的。
6.2.1.2 案 例 二
某企业A186G型梳棉机的波谱图如图8所示。

图8 生条异常波谱图
上车检查发现,其传动小压辊的皮带张力轮位置不正,每转动1周皮带产生1次松紧变化和位置摆动,影响对小压辊的传动效率,使生条产生1个三角波形态的粗细变化。调整张力皮带轮后,波谱图恢复正常。
6.2.2 非对称性非正弦波周期性疵点
6.2.2.1 单向脉冲波
传动齿轮齿缺损,在传动过程中产生打顿,在须条上会形成粗节或细节。且同齿轮连续缺齿的数量不同,罗拉顿挫的时间就不同,形成粗细节的大小也不同。如果是间隔性多个齿形缺损,有几个齿型缺损部位,在波谱图上就会形成几个周期性单向脉冲波,在波谱图上就会形成几组主波与谐波。在分析波谱图时,要注意主波与谐波的对应关系。
以直径为250 mm前罗拉的18齿轴头齿轮齿型损伤为例:若该齿轮损伤1个齿,理论计算该齿轮缺陷输出机械波的主波波长为250 mm×3.14=785 mm,该罗拉输出疵点长度约为785 mm/18=43.6 mm,在波谱图上会形成一组以785 mm为主波波长的包含偶次谐波和奇数谐波的图形;若该齿轮损伤2个齿,那么理论计算该齿轮缺陷输出的疵点长度仍为785 mm/18=43.6 mm,但齿轮转动1周会顿挫2次,输出2个疵点,因此会有两个主波,波长分别为250 mm×3.14×13/18=567 mm和250 mm×3.14×5/18=218 mm,在波谱图上会形成2组分别以567 mm和218 mm为主波波长的包含偶次谐波和奇数谐波的图形。
有时由于齿轮啮合不良或齿严重磨损,齿轮在运转过程中还会逐齿打顿,此时形成的机械波主波波长就是该齿轮每转动1个齿所输出的须条长度。
在纺纱流程中,可以产生类似疵点的问题主要有:胶圈与须条接触区域损伤;键或键槽损伤;牙齿槽隙塞嵌杂物;梳棉机锡林、道夫、刺辊针布局部损伤;罗拉沟槽损伤;齿形带齿形缺损;精梳机棉网搭接不良,等。
图9是某企业使用FA506A型细纱机生产R 18.4 tex品种时出现的疵点案例。
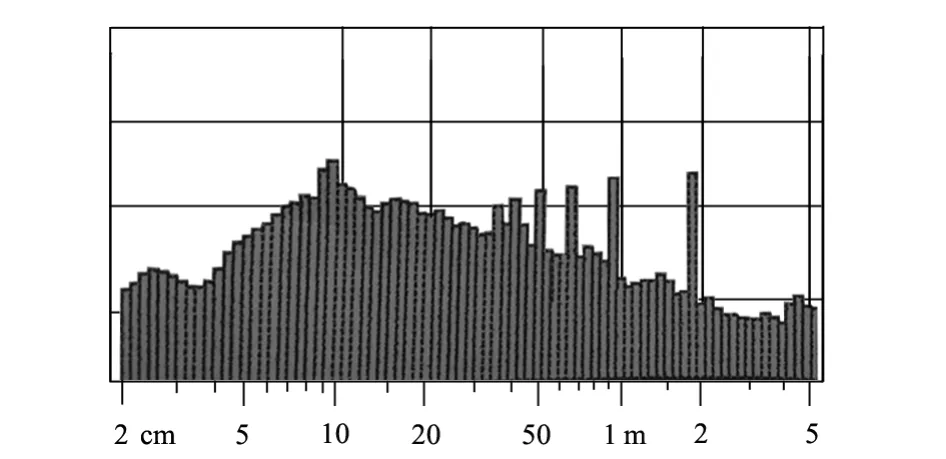
图9 FA506A型细纱机牵伸系统
传动出现的机械波
该品种的细纱工艺:ZD/ZE=52/81,ZM/ZH=29/27,ZJ/ZK=25/81;总牵伸倍数为27.66,后区牵伸倍数为1.136。根据FA506A型细纱机牵伸系统传动图,计算各部位的机械波波长可知,约为1.9 m的机械波应该是出现在中罗拉及中罗拉头部。经上车检查,发现中罗拉轴头齿轮有一个齿断裂。更换新的中罗拉轴头齿轮后测试,波谱图恢复正常。
6.2.2.2 锯 齿 波
纺纱过程中,如果机械部件运行速度或须条的张力出现不对称性波动,可能会造成锯齿波特性的疵点。如细纱机的卷绕成型机构采用非1∶1的成型凸轮时,由于钢领板的上升速度与下降速度不同,纱线在卷绕过程中受到的张力变化及钢丝圈对纱线的摩擦力都会形成不对称的变化曲线,可能造成纱线上毛羽呈类似锯齿波的变化曲线[3],其波谱图上就会出现偶次谐波和奇次谐波。
6.2.2.3 双向脉冲波
牵伸部件运转不稳定,如前胶辊损伤可能会在纱线上形成1个细节和1个粗节连续出现、间隔规律的双向脉冲周期性疵点。
这种疵点的波谱图除主波外,还有偶次谐波和奇次谐波。但比较特殊的是主波幅度会小于谐波的幅度,波幅最大的谐波次数,就代表了主波波长与疵点本身长度(指粗节和细节的总长度)的比例。如波幅最大的谐波为5次谐波,那么粗、细节的总长度就等于主波波长的1/5,如果主波长度为1 m,那么粗、细节总长度就约为20 cm(也就是说波幅最大的谐波所在的频道位置所代表的波长,就等于粗、细节的总长度)。
粗纱胶辊损伤后生产细纱时的曲线图和波谱图,见图10和图11。

图10 粗纱胶辊损伤后生产细纱的曲线图
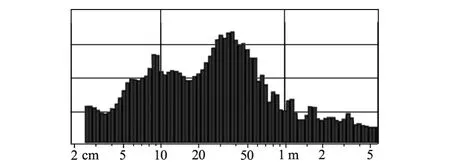
图11 粗纱胶辊损伤后生产细纱的波谱图
从曲线图10可明显看到存在双向脉冲波,主波波长约为3.5 m。从波谱图11可以看出主波约为3.5 m,其左侧分别存在2次、3次、4次,…谐波;且在30 cm~60 cm形成了谐波集聚,看上去像是牵伸波,振幅最高的是8次谐波,其所在的频道代表波长约为48 cm。所以,纱的粗、细节长度约为48 cm,这一点在络筒机上通过电清统计的事件报告也可以得到证实。
7 结语
波谱图分析需要细心,应结合曲线图、DR图、长度—变异曲线图等仔细分辨图形的特征,根据有无谐波、谐波类型和谐波包迹线形态等特点,认真辨别疵点的类型,并通过生产实践进行验证。
