立足数学建构,提高复习效率
——以“27.2相似三角形(复习课第1课时)”为例
2019-09-25湖北省利川市教学研究和教师培训中心罗仁义
☉湖北省利川市教学研究和教师培训中心 罗仁义
复习教学难,复习教学的整体设计更难.在新授课时,由于受教学时间的限制,我们不得不将数学整体知识拆分成几个甚至十几个课时进行教学,而学生在这一段时间内学习的数学知识是零散的,缺乏系统性.为了克服新授课时的弊端,复习教学必须及时,复习教学必须统筹设计.如果复习教学能使学生整体把握所学知识,建立学生自己的数学认知结构,那么,这样的复习教学一定能够提高复习的效率.本文以利川市团堡初级中学龚志老师执教的“27.2相似三角形(复习课第1课时)”为例,与同行探讨基于建构论的初中数学复习教学方法.
一、教学过程
1.复习引入
师生活动:
(1)构建知识框图(本课以对比表和对比图的方式给出).

表1

(2)在知识框图的基础上,引导学生回顾和梳理知识点.
(3)学生结合图表,叙述相似三角形判定定理.
(4)引导学生对知识进行回顾和梳理,回答不了的请看书后再回答.
教学点评:
(1)知识框图由师生共同较快给出,让学生从新的角度整体感知本节的知识点,避免知识的简单重复,帮助学生建立数学认知结构.
(2)通过全等三角形和相似三角形的对比,引导学生对知识进行回顾和梳理,复习相似三角形的定义、判定及性质,比较新、旧知识的异同,促成新、旧知识间的正迁移.让学生从记忆中提取知识,回答不了的看书后再回答,进一步理解、记忆相似三角形的相关知识.
2.问题探究
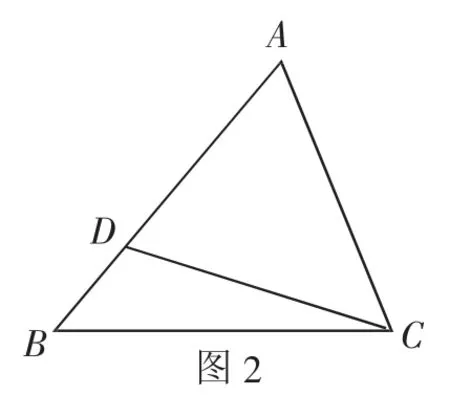
问题1:如图2,要使△ABC与△ACD相似,需补充的条件是_________(只要写出一种).
师生活动:
(1)分析:已有∠A=∠A,要使△ABC与△ACD相似,可以添加一角相等或夹这角的两边对应成比例.
(2)提问:怎样添加与角有关的条件使三角形相似?怎样添加与边有关的条件使三角形相似?
(3)师生交流思考过程.
(4)学生独立思考添加的条件及解题依据.
教学点评:
(1)教师引导学生回顾已学知识,帮助学生复习三角形相似的判定方法,形成新的数学认知结构.
(2)学生经历思考和解决开放问题的过程,逐步领会解决开放型问题的方法.
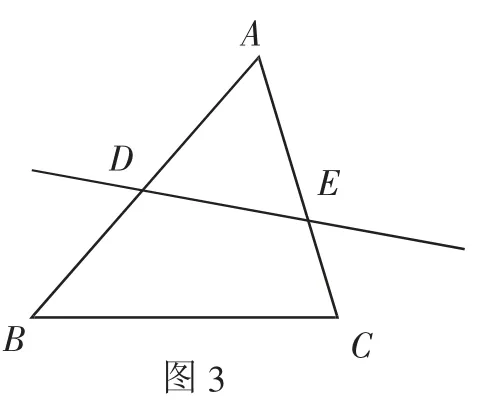
问题2:如图3,一条直线分别与△ABC的边AB和AC交于点D和E,请添加一个条件,使△ABC与△ADE相似,有几种添法?并说明理由.
师生活动:
(1)类比问题1的学习方法,引导学生分别从角和边的角度添加条件,使两三角形相似.
(2)学生先思考,然后小组讨论,最后小组展示.
(3)学生回答添加的条件和证明的依据,教师做相应的点评和小结.
教学点评:
(1)解决问题2时,让学生再次对复习的知识进行回顾,有利于进一步巩固复习的知识.
(2)类比问题1分析问题2,找到添加不同的条件使三角形相似的多种方法,复习三角形相似的判定方法.引导学生利用多种方法判定三角形相似,体会方法的多样性,培养学生的发散思维能力.

3.典型例题
例1在△ABC中,D、E分别是AB、AC反向延长线上的点,BC∥DE,求证:AB·AE=AC·AD.
师生活动:
(1)审题.分析题目中的已知条件和隐含条件,明确要求解答的问题.
(2)厘清解题思路.师生互动共同归纳:要证明AB·AE=AC·AD,先把等积式变为比例式.要证明比例式,就是要证明三角形相似,而由平行可以得到三角形相似.
(3)写出解题过程.学生独立完成例1的解答,教师根据学生展示的解题过程,逐步规范解题格式.
(4)反思并总结解题方法.
教学点评:
(1)巩固由平行得到三角形相似的判定方法,由三角形相似的性质得到对应线段成比例等知识点.
(2)师生共同分析,让学生知道由已知条件获取有用信息的方法,引导学生体会根据结论步步逆推,直至所需条件能与题中已知条件建立联系的思维方法,进而获得解题的思路,培养学生的逆向思维能力.
(3)教师根据学生展示的解题过程,规范解题的书写格式,为学生后面的学习做示范.
(4)根据解决问题的一般过程,引导学生反思本题的解题过程,培养学生的思维品质,养成良好的解题习惯.
例2如图5,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4.求证:



师生活动:
(1)学生举手回答证明第(1)问.
(2)对于第(2)问,引导学生先找∠ABC=∠DBE,再找夹这个角的两边对应成比例,从而证明三角形相似.
(3)学生写出证明过程.
教学点评:
(1)在例1的基础上,调动学生学习的主动性,让学生体会证明“旋转型”三角形相似的方法,复习三角形相似的判定和性质.
(2)证明第(1)问的条件容易找到,证明第(2)问的条件较难发现.证明第(2)问要利用证明第(1)问所得对应线段的比例式,交换两内项(或外项)得到新的对应线段的比例式,这也是在证明相似三角形的过程中寻找条件时常用的方法.例2的难度逐渐加大,让学生“跳一跳,摘到桃”,激发学生的学习热情.
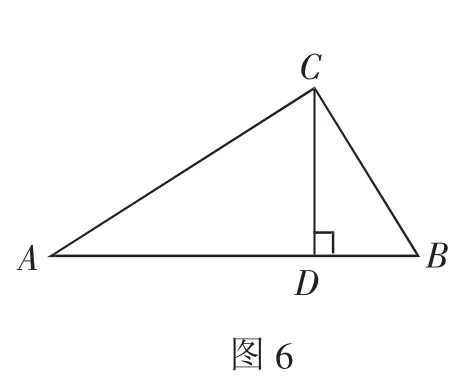
例3如图6,在Rt△ABC中,CD是斜边AB上的高.
(1)图中有几个直角三角形?
(2)图中有哪几对相似三角形?找出其中一对并加以证明;
(3)若AB=10cm,BC=4cm,求BD的长.
师生活动:
(1)先由学生参照例1和例2,分析本题的解题思路,然后由学生独立完成,再由小组交流,最后由学生代表展示解题步骤.教师在此过程中注意引导.
(2)在此题中,教师要注意强调相似三角形对应的顶点要写在对应的位置.
教学点评:
(1)进一步训练证明三角形相似的思路和方法,提高学生分析和解决问题的能力.
(2)利用三角形相似的知识解决数学问题,体现知识的应用价值.
(3)回顾解题思路,总结解题方法,提升分析问题和解决问题的能力.

4.课堂监测:
如图7,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,∠APD=60°.
(2)求CD的长.
教学点评:
学生独立完成,检查复习效果,为复习课第2课时的教学做铺垫.
5.课堂小结
师生活动:你学到了什么?
(1)说说三角形相似的判定和性质.
(2)你是如何找出并证明两个三角形相似的?
(3)说说几种相似的基本图形,并说说如何运用相似三角形的判断和性质解决问题.
(4)谈谈解决问题的主要步骤有哪些.
教学点评:
通过对相似三角形知识的再次梳理,有利于学生的认知结构呈螺旋式结构发展;通过对解题思路的分析和叙述,有利于培养学生的逻辑思维和推理论证能力;通过对解题方法和过程的回忆,有利于学生积累解决问题的方法;通过对解题步骤的归纳和总结,有利于培养学生分析问题和解决问题的能力.
二、教学立意的进一步阐释
1.基于数学认知结构,积极引导学生建构
如何上好数学复习课?这是教师一直感到困惑的教学问题,原因在于很容易把复习课上成“炒现饭”式的简单重复课,这样的课学生觉得淡而无味,教师也感到毫无新意,更重要的是难以达到“巩固提高”的复习教学目标.本课的教学设计,特别是“复习引入”部分基于建构教学理论的设计,让我们看到了复习教学的有效途径和策略——教师从新、旧知识间的区别和联系入手,基于建构的教学设计,这样的复习课具有了新的内涵;学生从整体出发自主复习已学知识,进一步理解知识的本质,这样的复习课具有了新的意义;学生从新的角度去比较和思考已学知识,建立自己的数学认知结构,这样的复习课具有了新的高度.
2.注重复习的及时性,提高学生数学素养
当新学知识积累到一定量的时候,有计划地组织复习教学是必须的,按认知理论的观点,复习应贯穿于学习过程的始终.本节课是“27.2相似三角形”的复习课,通过相似三角形与全等三角形相关知识的对比,巧妙地促成了知识间的正迁移,既复习了三角形相似的判定和性质,又进一步巩固了三角形全等的相关知识.学生先后学习的知识得以重新建构,有利于优化学生的数学认知结构,从而提高学生的数学素养.
3.引导反思解题过程,力争做到举一反三
在典型例题的教学中,重点强调解题的思路和方法.分析思路时,除综合分析方法外,直观猜想、逆向分析、合情推理等也是行之有效的分析方法,能培养学生数学思维的品质.问题解决后,引导学生回顾解题过程,让学生总结和体会解题的一般步骤:审清题意—分析解题的思路—写出解题过程—反思并总结解题方法,体现了解决问题的一般规律.
