Relative Position and Attitude Control for Drag-Free Satellite with Prescribed Performance and Actuator Saturation

TAO Jiawei，ZHANG Tao

Department of Automation，Tsinghua University，Beijing 100084，P.R.China

Abstract: An adaptive prescribed performance control scheme is proposed for the drag free satellite in the presence of actuator saturation and external disturbances. The relative translation and rotation dynamics between the test mass and outer satellite are firstly derived. To guarantee prescribed performance bounds on the transient and steady control errors of relative states，a performance constrained control law is formulated with an error transformed function. In addition，the requirements to know the system parameters and the upper bound of the external disturbance in advance have been eliminated by adaptive updating technique. A command filter is concurrently used to overcome the problem of explosion of complexity inherent in the backstepping control design. Subsequently，a novel auxiliary system is constructed to compensate the adverse effects of the actuator saturation constrains. It is proved that all signals in the closed-loop system are ultimately bounded and prescribed performance of relative position and attitude control errors are guaranteed. Finally，numerical simulation results are given to demonstrate the effectiveness of the proposed approach.

Key words: relative position and attitude control; drag-free satellite; command filter; prescribed performance;actuator saturation

0 Introduction

The drag-free satellite acts a pivotal part in many science missions including the test of equivalence principle，the detection of gravitational waves and the measurement of the earth gravity field.Pugh［1］firstly proposed drag-free concept，then it was studied systematically by Lange［2］. Specifically，the great application prospects and importance of drag -free flight have been gradually shown in many missions such as the MICROSCOPE satellite［3］，the satellite test of the equivalence principle（STEP）［4-5］，the gravity probe B（GP-B）satellite［6-7］，the laser interferometer space antenna（LISA）satellite［8］，the LISA Pathfinder satellite［9］，the gravity field and ocean circulation explorer（GOCE）satellite［10-11］and so on.

The drag-free satellite contains a cavity in which a test mass is shielded by the surrounding spacecraft against the external environment disturbances. This structure provides a free-falling environment for the inside floating test mass，and the key technology is to control the outer spacecraft to chase the test mass in its purely gravitational motion. With the development of drag-free missions，a wide variety of studies about the drag-free control have been carried out.

Some control techniques including PID which lacks explicit disturbance rejection and H∞/H2［12-13］have been treated to design drag-free control scheme.

The model predictive control method was adopted to tackle the drag free control problem of GOCE satellite［14］，where the plant's six degrees of freedom had to be decoupled into four linearized systems.

A robust controller based on a simplified uncertain design plant with given structure for a plant describing a drag-free satellite was developed［15］. The designed optimal single-input-single-output controllers can robustly achieve the desired level of performance.

The Embedded Model Control（EMC）technique［16］was proposed by Canuto and then investigated to resolve the drag-free and attitude control problem of GOCE satellite［17］. The core of this control design and algorithm was the embedded model which defines three interconnected parts including the controllable dynamics，the disturbance class to be rejected and the neglected dynamics.

A control strategy that used the on-orbit timedependent change in angle of attack for a new type of super-low-altitude flight was developed［18］. This partial drag-free flight had potential applications in some stealth military missions.

Although many schemes as mentioned above have been presented for the drag-free control design， it is always assumed that the couplings among the different degrees of freedom are highly reduced or treating them as unknown disturbance.Nevertheless，it is important to note that the behavior between the test mass and outer satellite can be regarded as a formation. The relative position and attitude are mutually coupled，especially for dragfree satellite with cubic test mass，because the relative attitude motion between the test mass and the outer satellite can be neglected for drag-free satellite with spherical test mass；besides，the thrust control system is the key unit to achieve drag-free flight by providing a precise compensation for the disturbing force except gravity. The performance of a new cusped field thruster was tested and analyzed［19］，then a drag-free control scheme based on the cusped field thruster was designed to evaluate the performance of this thruster. The thruster limitation effect is a potential problem for control system design. It often severely deteriorates system performance，even leads to undesirable inaccuracy or instability.

In this paper，the integrated relative position and attitude motion between the cubic test mass and outer satellite is firstly derived. Taking model parameters uncertainty，external environment disturbance and actuator saturation into consideration，an integrated position and attitude control strategy with prescribed performance is designed by integrating adaptive technique，command filter，anti-wind technique and prescribed performance control theory.During the control design，the requirements to know the accurate system parameters and upper bound of the external disturbance are eliminated，and the tedious analytic computations of time derivatives of virtual control laws are canceled. It is proved that the proposed control can guarantee the prescribed performance of the relative position and attitude irrespective the presence of actuator saturation.

1 Mathematical Model and Problem Formulation

In this section，in order to realize precise tracking of test mass in a drag-free satellite，the dynamics of the relative motion between the test mass and the outer satellite is derived.

Considering the displacement mode of drag -free satellite with single cubic test mass，the relative attitude kinematics can be expressed as［20］

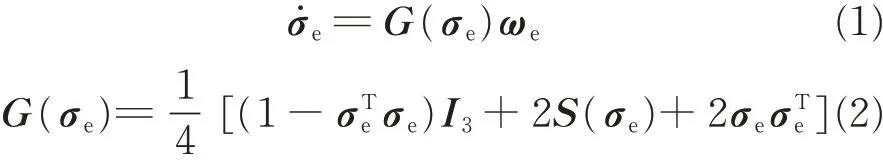
where σeis the modified rodrigues parameters（MRP）vector representing the relative attitude between the test mass and the outer satellite，and ωe=ωs-R(σe)ωtis the relative angular velocity between outer satellite body frame Fsand the test mass body frame Ftexpressed in frame Ft. The rotation matrix from Fsto ℱtis

Further，the relative attitude dynamic can be governed by［21］

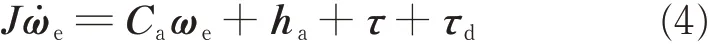
where skew symmetric matrix Caand nonlinear term haare expanded as

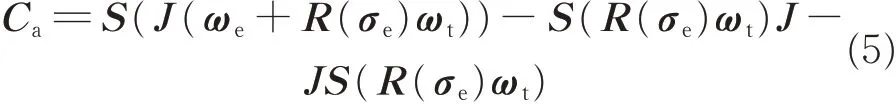
and

The relative position vector between frame Fsand frame Ftis denoted as

The relative position kinematics and dynamics can be represented as［22］

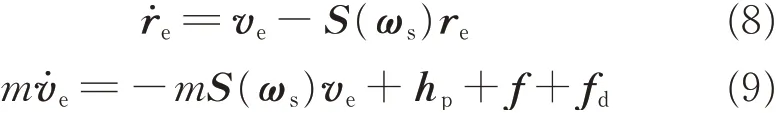
where nonlinear term hpis

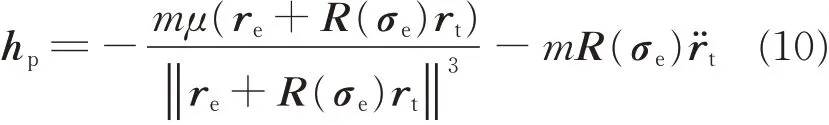
From Eqs.（8）and（9），we can see the relative translational dynamics has the item of the relative rotational dynamics. Therefore，the relative translational motion is coupled with rotational motion.

In order to facilitate the control system design process，the following assumptions and lemmas will be used in this paper.

Assumption 1The disturbance vectors fdand τdare unknown but bounded with unknown bounds.

Assumption 2The unknown mass m and inertial matrix J satisfies

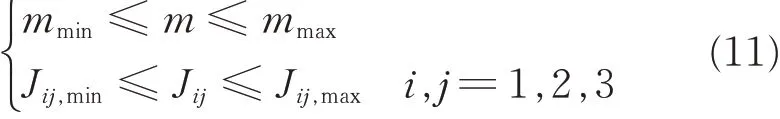
Assumption 3To satisfy the actuator saturation constraint，the real control inputs f and τ are determined by the saturated function of commanded control force fcand control torque τc，that is

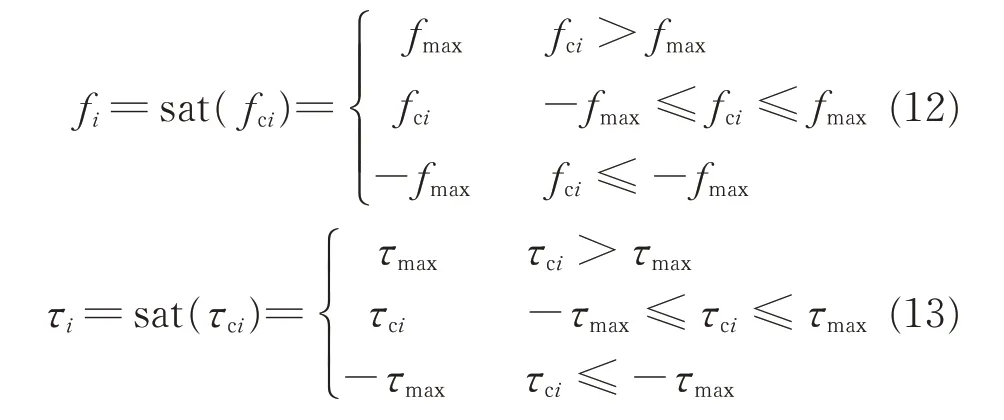
Lemma 1For arbitrary constant ε ＞0 and variable a，the following inequality always holds［23］

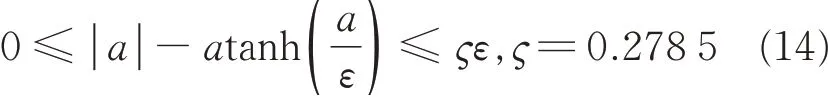
Lemma 2Given any smooth function α(t)，its derivative can be estimated by the following twoorder command filter［24］

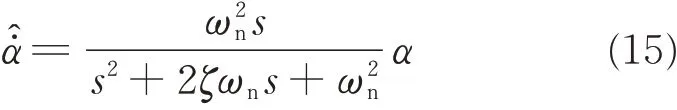
Choosing an appropriate damp ratio ζ and a sufficiently large natural frequency ωncan ensure the accurate approximation［25］.

The control objective of this paper is to design a control scheme based on the system formulated by Eqs.（1），（4），（8）and（9）without resorting to the exact knowledge of the mass and inertia parameters and despite the presence of external disturbance and actuator saturation such that：

（1） The relative position and attitude error achieve prescribed transient and steady-state performance.

（2）The ultimate boundedness of all closedloop signals are guaranteed.

2 Controller Design

In this section，detailed design procedures via backstepping technique are presented to achieve the control objective.

2.1 Relative attitude controller design

The prescribed performance of relative attitude is achieved by ensuring that tracking error σeevovles strictly within predefined bounds as follows

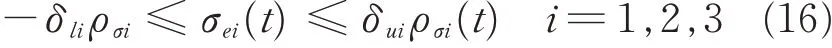
where 0 ＜δli，δui≤1 are positive constants，ρσi(t)is the chosen prescribed performance function for attitude system. In this work，the exponentially decaying performance function are chosen as［26］

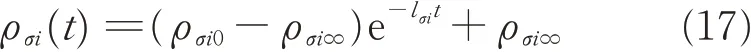
where ρσi0，ρσi∞and lσiare strictly positive constants.Denote

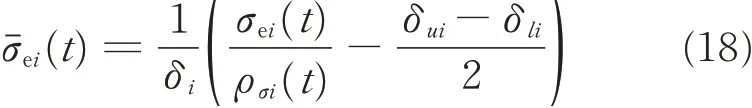
where δi=(δui+δli)/2. Based on Eqs.（16），（18），it implies

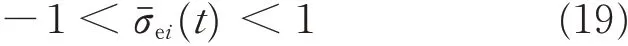
In order to transfer the prescribed performance control problem（19）to a normal unconstrained one，an error transformation is employed as

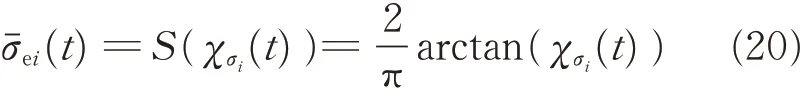
Since S(χσi(t) ) is strictly monotonic increasing，the inverse function of S(χσi(t) ) exists. Then，the transformed error χσi(t) can be expressed as

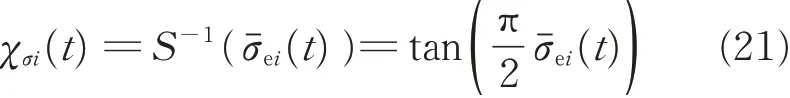
Invoking Eqs.（18）and（21），we have

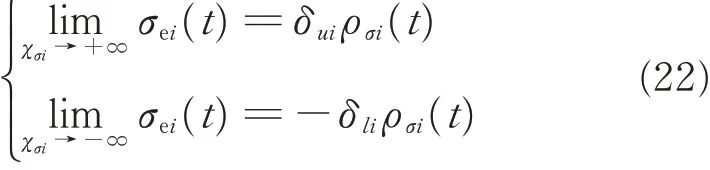
From Eq.（21），we can obtain

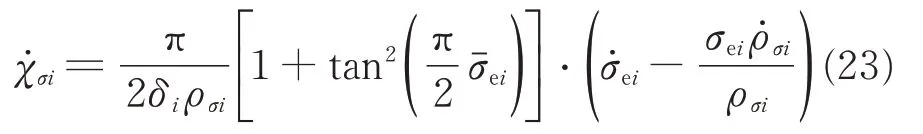
Denote

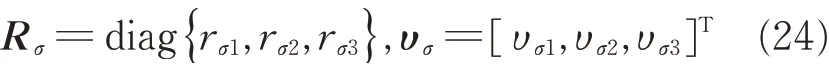
Then from Eqs.（1），Eq.（23）can be written in compact form as

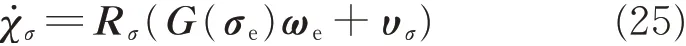
Then，the problem of achieving prescribed performance of relative attitude error has been converted into designing a control scheme to ensure the boundedness of the transformed error σe. In what follows，the following coordinate changes are firstly employed

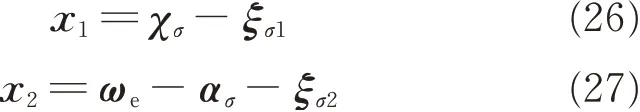
where ασis the virtual control signal to be designed latter；ξσ1the compensation term satisfying

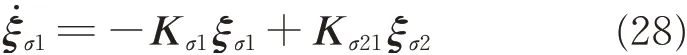
where Kσ1and Kσ21are positive matrixes. The new signal ξσ2is introduced to deal with the saturation effect through following novel auxiliary system

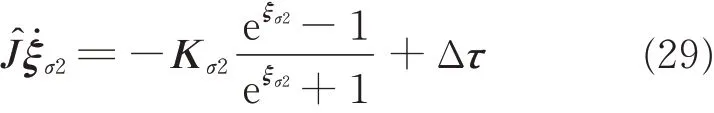
where Kσ2is a positive matrix，J^ the estimate of J，Δτ=τ-τcthe difference between commanded and actual control torque.

Considering Eqs.（26），（27）and（28），the time derivative of x1can be expressed as

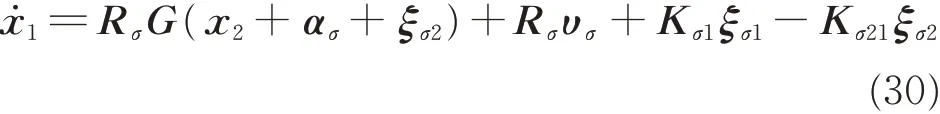
The virtual control law ασis designed as

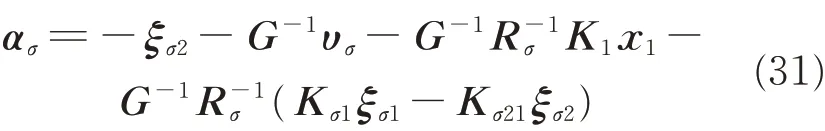
where K1is a positive matrix. Choosing the following Lyapunov function candidate

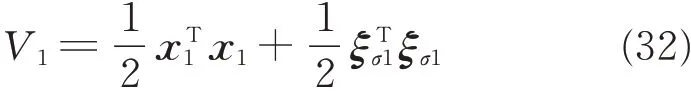
Considering Eqs.（28），（30）and（31），the time derivative of V1is given by

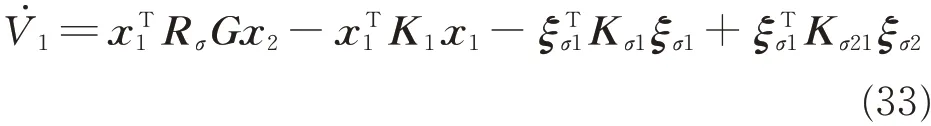
To overcome the explosion of complexity caused in backstepping design，introducing a new variableas the output of a command filter（15），and passing the virtual control（31）through it produces

Taking the derivative of Eq.（27），then from Eqs.（4）and（34），we have

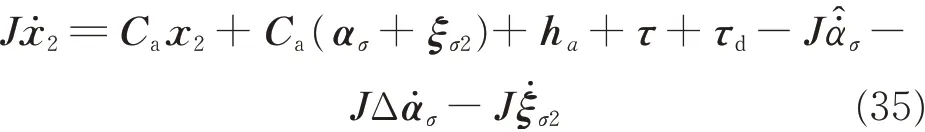
From Assumption 2，a linear operator L(·)：R3→R3×6acting on an arbitrary vector α=[ a1a2a3]Tis introduced to isolate the unknown inertia matrix J such that

where

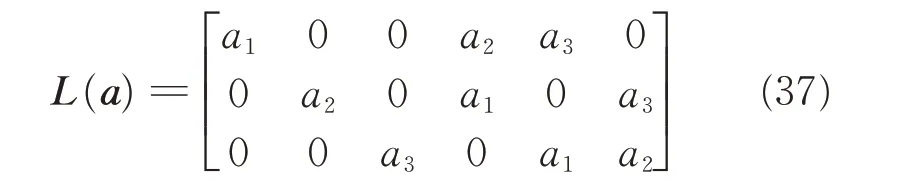
and

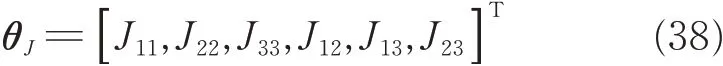
From Eq.（36），we know

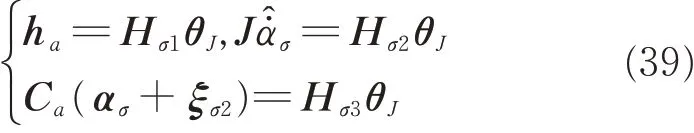
where

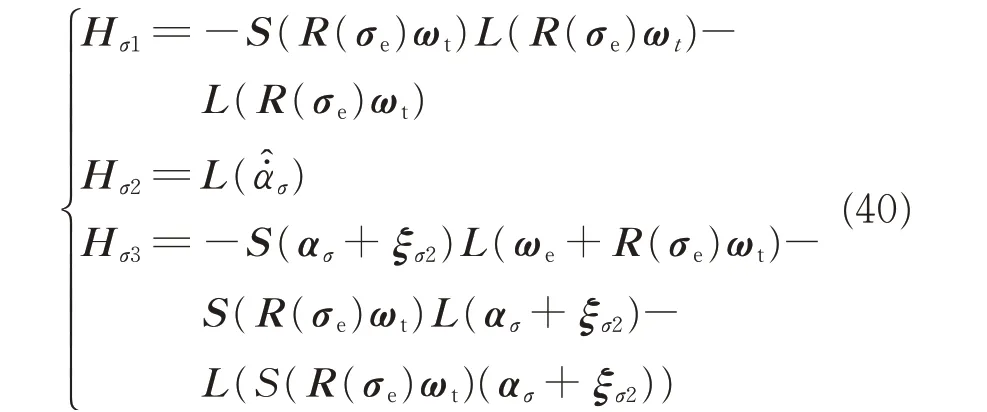
In view of Eqs.（13），（34）and（39），Eq.（35）can be rewritten as

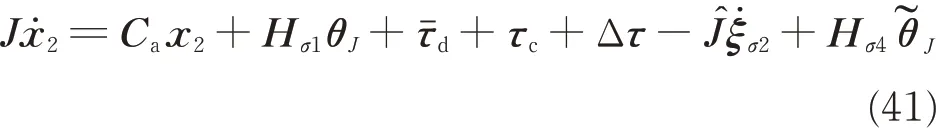
According to Assumption 1 and Lemma 2，τˉdis bounded，namely，≤ησi(i=1，2，3). Then，we can design the relative attitude control input τcas

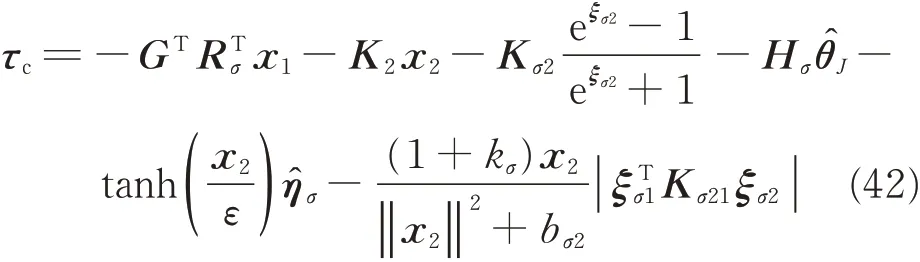
where K2=KT2is a symmetric matrix. Design adaptation laws foras

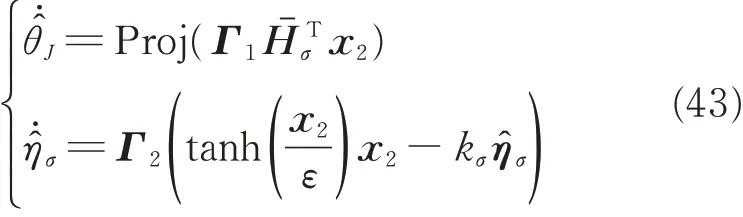
where the Proj(·) is a Lipschitz continuous projection algorithm［27］，=Hσ-Hσ4，Γ1and Γ2are positive define matrixes. Moreover， the notation tanh(·) is defined as

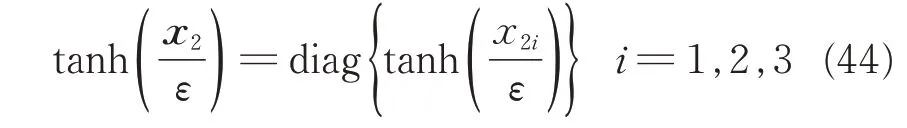
Define the estimate error of

then a Lyapunov function is constructed as

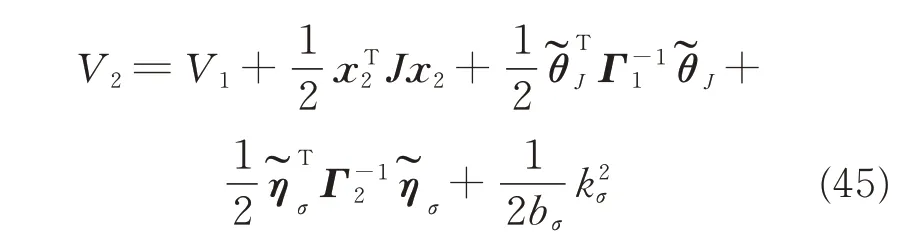
where kσis the auxiliary variable［28］satisfying

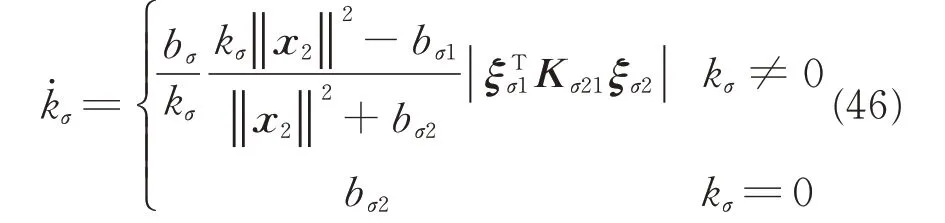
The derivative of Eq.（45）can be derived as

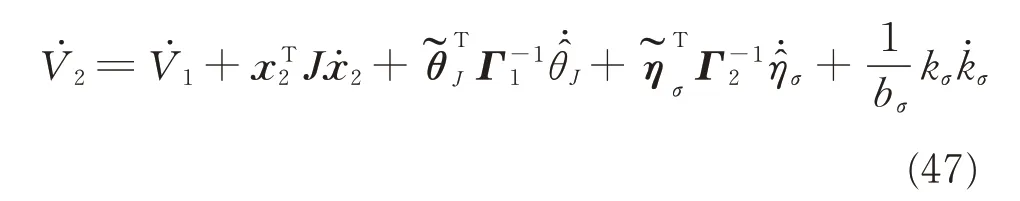
Substituting Eqs.（33），（41），and Eq.（42）into（47）and considering xT2Cax2=0 yields

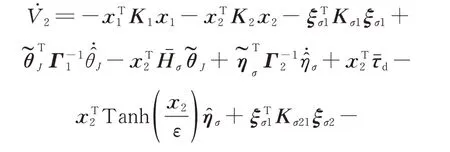
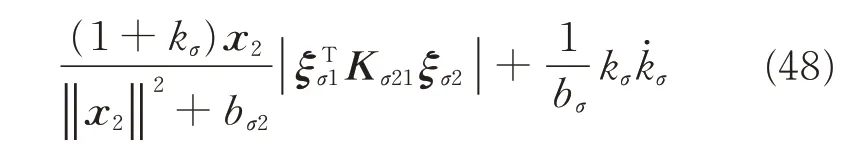
According to Lemma 1，we have

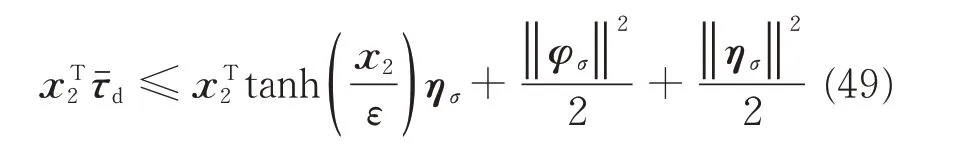
where φσ=[ςε，ςε，ςε]T.

Applying to the property of projection operator，the following inequality holds

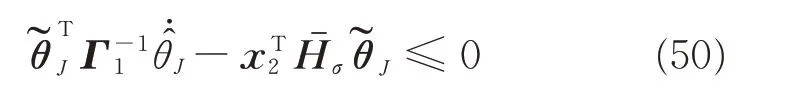
In virtue of Eqs.（49）and（50），substituting Eqs.（43）and（46）into Eq.（48），we have

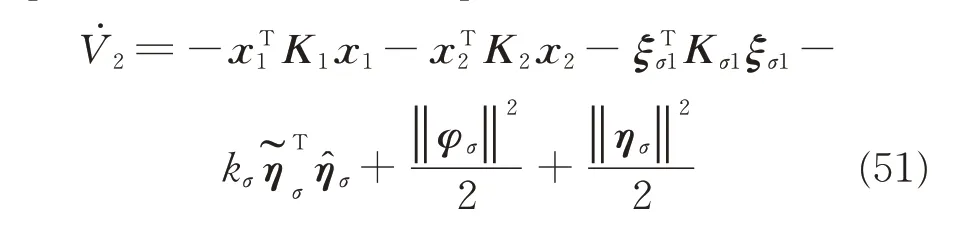
From Schwartz inequality，the following inequality can be obtained

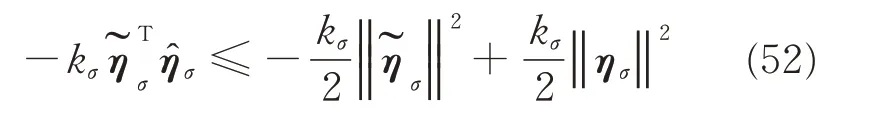
Hence，substituting Eq.（52）into Eq.（51），one has the following inequality

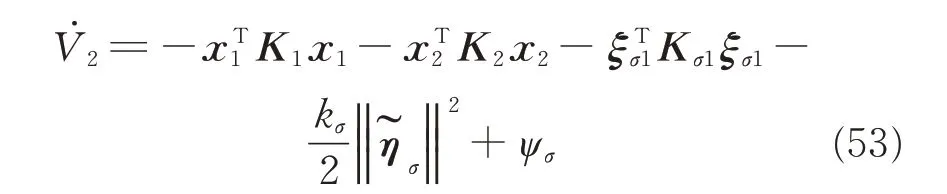
From Eq.（53），the stabilization of the transformed relative attitude systems（4）and（25）is ensured，then the relative attitude error can be guaranteed within prescribed performance bounds in Eq.（16）. The main result is summarized in the following theorem.

Theorem 1Consider the relative attitude dynamic systems（1）and（4）under the control torque constraint（13）with Assumptions 1—3，the proposed controller（42），adaptation laws（43）and（46）can guarantee that all signals in the closed-loop system are uniformly ultimately bounded，and the relative attitude error remains within the prescribed performance bounds all the time.

2.2 Relative position controller design

The prescribed performance of relative position is achieved by ensuring that tracking error reevolves strictly within predefined bounds as follows：

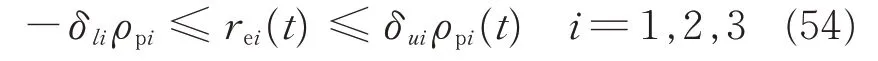
where the exponentially decaying performance function ρpi(t) are chosen as［26］

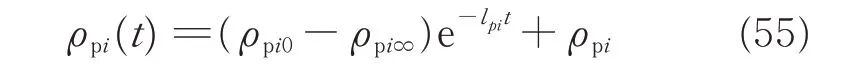
where ρpi0，ρpi∞and lpiare strictly positive constants.

Denote

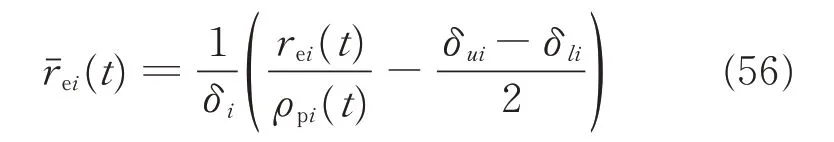
where δi=(δui+δli)/2. Based on Eqs.（54）and（56），it implies

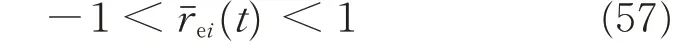
In order to transfer the prescribed performance control problem （57） to a normal unconstrained one，an error transformation is employed as

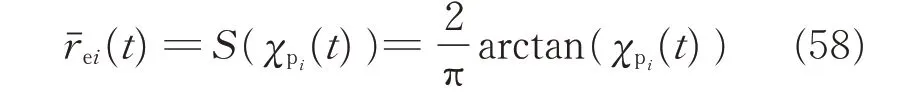
Since S(χpi(t) ) is strictly monotonic increasing，the inverse function of S(χpi(t) ) exists. Then，the transformed error χpi(t) can be expressed as

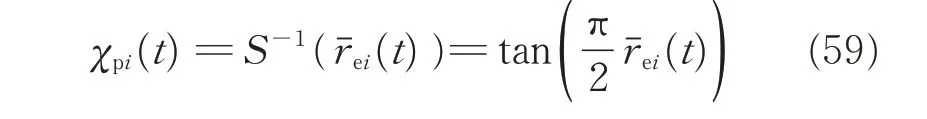
Invoking Eqs.（56）and（59），we have

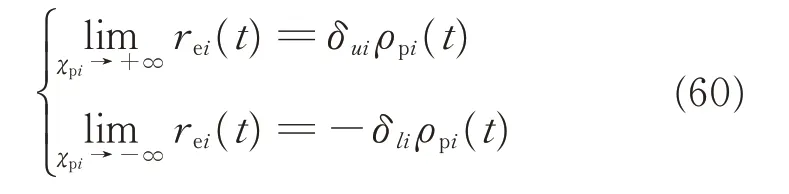
From Eq.（59），we can obtain

Denote

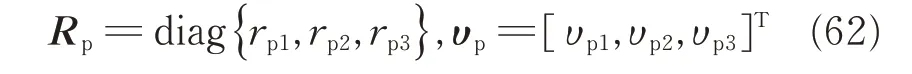
Then from Eq.（8），Eq.（61）can be written in compact form as

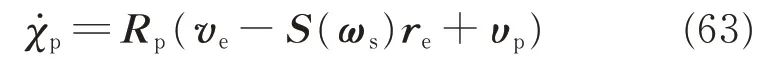
Then，the problem of achieving prescribed performance of relative position error has been converted into designing a control scheme to ensure the boundedness of the transformed error re.

Define the following coordinate changes

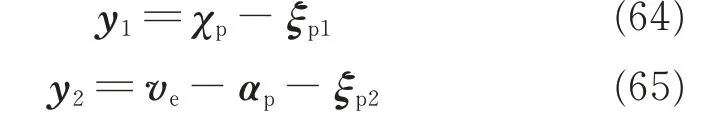
where αpis the virtual control signal to be designed laer；ξσ1is the compensation term satisfying

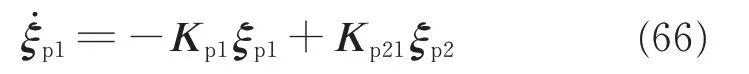
where Kp1and Kp21are positive matrixes；The new signal ξp2is introduced to deal with the saturation effect through following novel auxiliary system

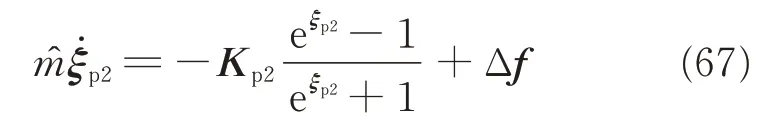
where Kp2is a positive matrix，m^ the estimate of m，Δf=f-fcdenotes the difference between commanded and actual control force.

Considering Eqs.（64），（65）and（66），the time derivative of y1can be expressed as

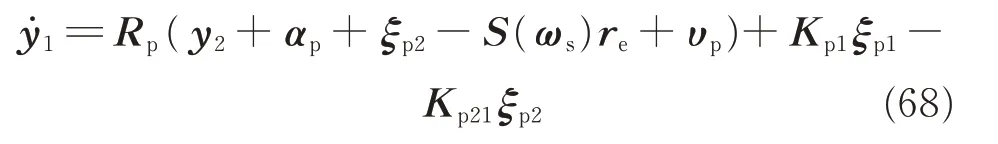
The virtual control law αpis designed as

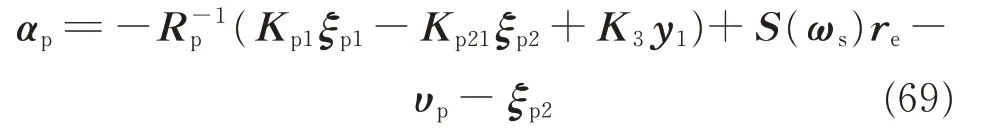
where K3is a positive matrix. Choosing the following Lyapunov function candidate

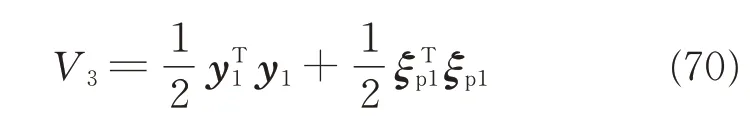
Considering Eqs.（66），（68）and（69），the time derivative of V3is given by

To overcome the explosion of complexity caused in backstepping design，introducing a new variableas the output of a command filter（15），and passing the virtual control（69）through it produces

Taking the derivative of Eq.（65），then from Eqs.（9）and（72），we have

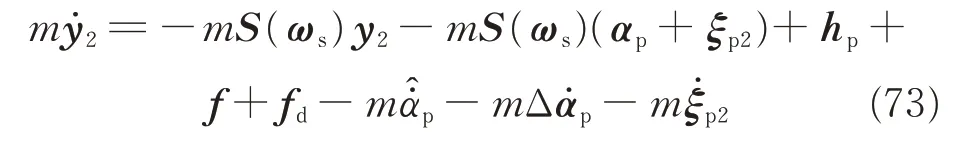
From Assumption 2，following relations is introduced to isolate the unknown mass m such that

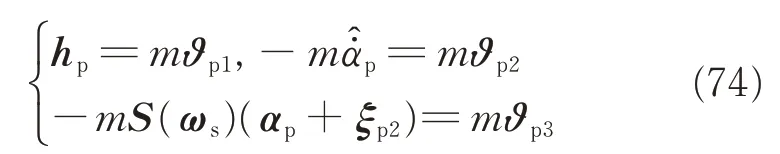
where

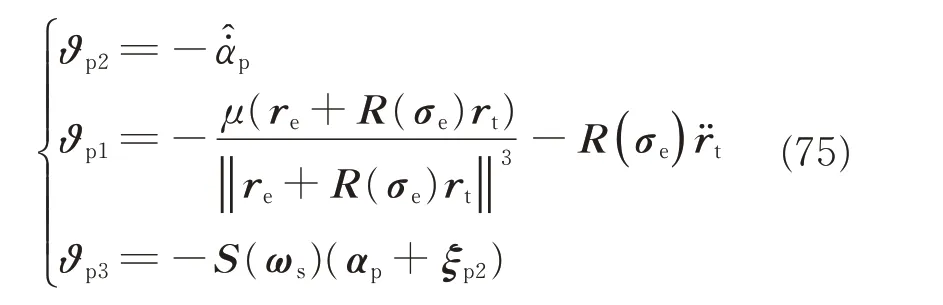
In view of Eqs.（12），（72）and（74），Eq.（73）can be rewritten as

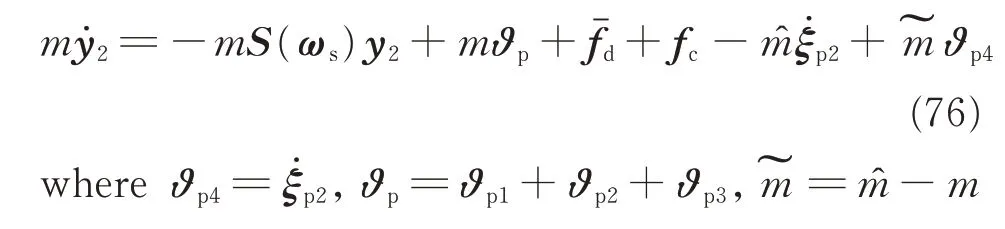
is the estimate error of m and=fd-is the lumped uncertainty.

According to Assumption 1 and Lemma 2is bounded，namely，(i=1，2，3). Then，we can design the relative position control input fcas

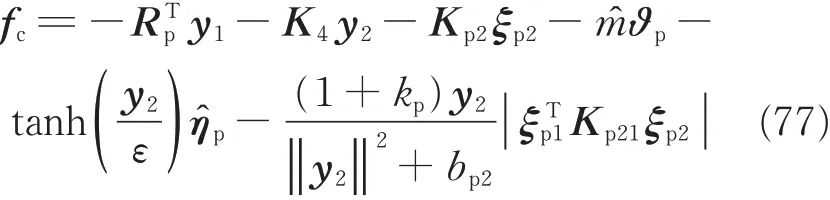
where K4=KT4is a symmetric matrix. Design adaptation laws forandas

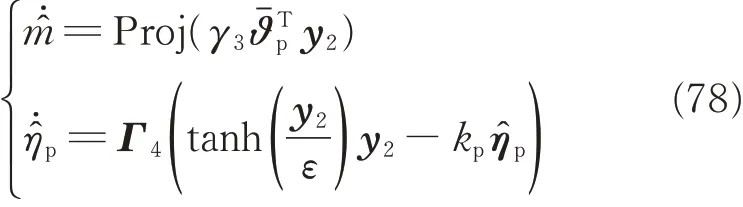
Define the estimate error of ηpasthen a Lyapunov function is constructed as

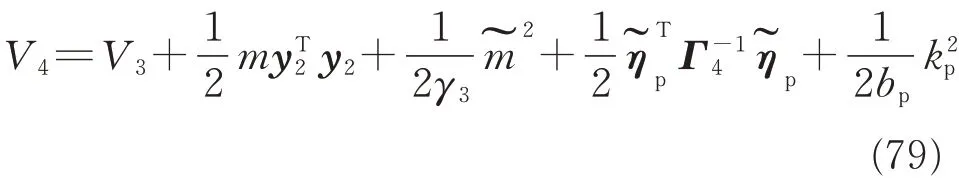
where kpis the auxiliary variable［28］satisfying

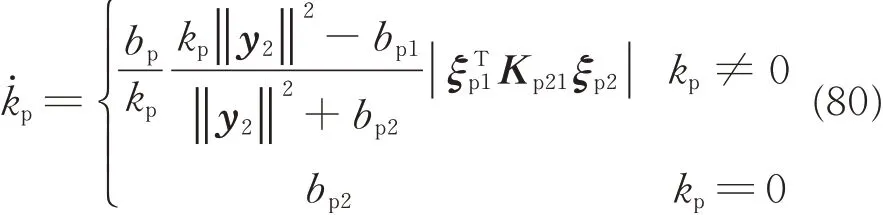
The derivative of Eq.（79）can be derived as

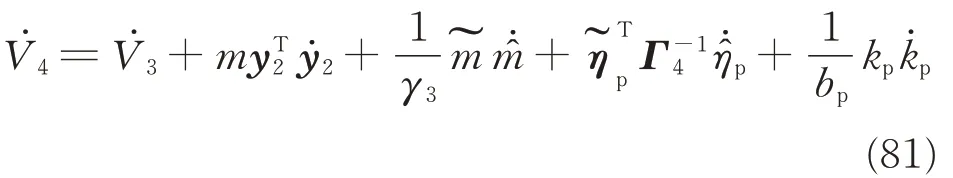
Substituting Eqs.（71），（76），and（77）into Eq.（81）and considering yT2S(ωs)y2=0 yields

According to Lemma 1，we have

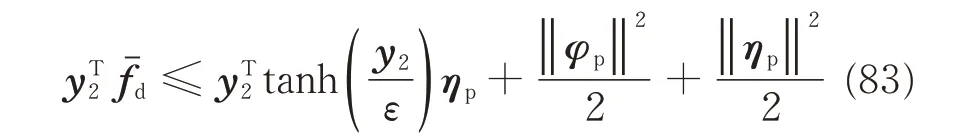
where φp=[ςε，ςε，ςε]T.

Applying to the property of projection operator，the following inequality holds

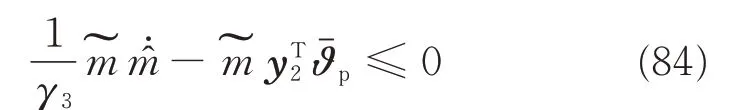
In virtue of Eqs.（83）and（84），substituting Eqs.（78）and（80）into Eq.（82），we have

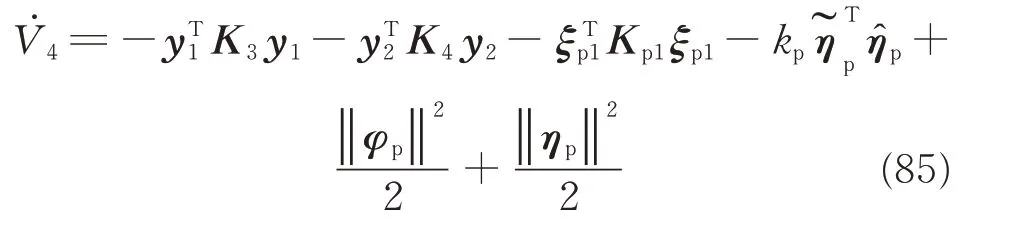
From Schwartz inequality，the following inequality can be obtained

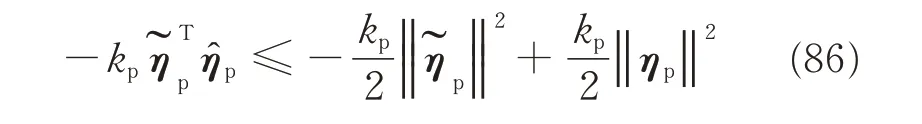
Hence，substituting Eq.（86）into Eq.（85），one has the following inequality

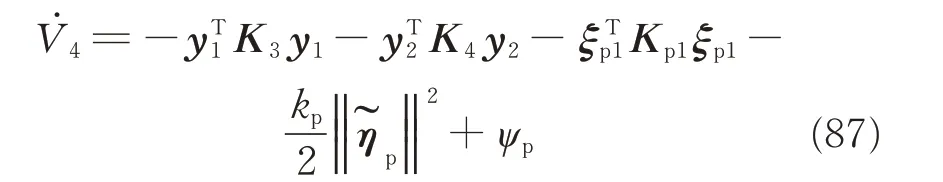
From Eq.（87），the stabilization of the transformed relative position systems（9）and（63）is ensured，then the relative attitude error can be guaranteed within prescribed performance bounds in Eq.（54）. The main result is summarized in the following theorem.

Theorem 2Consider the relative position dynamic systems（8）and（9）under the control force constraint（12） with Assumption 1—3，the proposed controller（77），adaptation laws（78）and（80）can guarantee that all signals in the closed-loop system are uniformly ultimately bounded，and the relative position error remains within the prescribed performance bounds all the time.

3 Numerical Simulations

In this section，a simulation scenario is considered to show the effectiveness and superiority of the proposed adaptive prescribed performance control scheme. Assume the drag free satellite is flying in a low orbit with the altitude 260 km. Then，the orbit angular velocity of the test mass is obtained as ωt=

The mass and the inertia matrix of the outer satellite are respectively assumed to be m = 20 kg and

The initial relative position and attitude are respectively characterized by

The disturbance force and torque are respectively modeled as

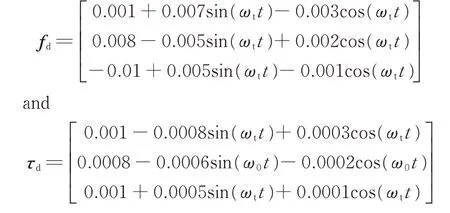
The control magnitude constraints are selected as fmax=10 N and τmax=5 N ·m. The parameters of control law，updating law，command filter and auxiliary system are set as shown in Table 1.

Choosing the chosen parameters of predefined performance bounds δui，δlias δui=δli=1. The prescribed performance functions for relative positionand attitude systems are respectively selected as

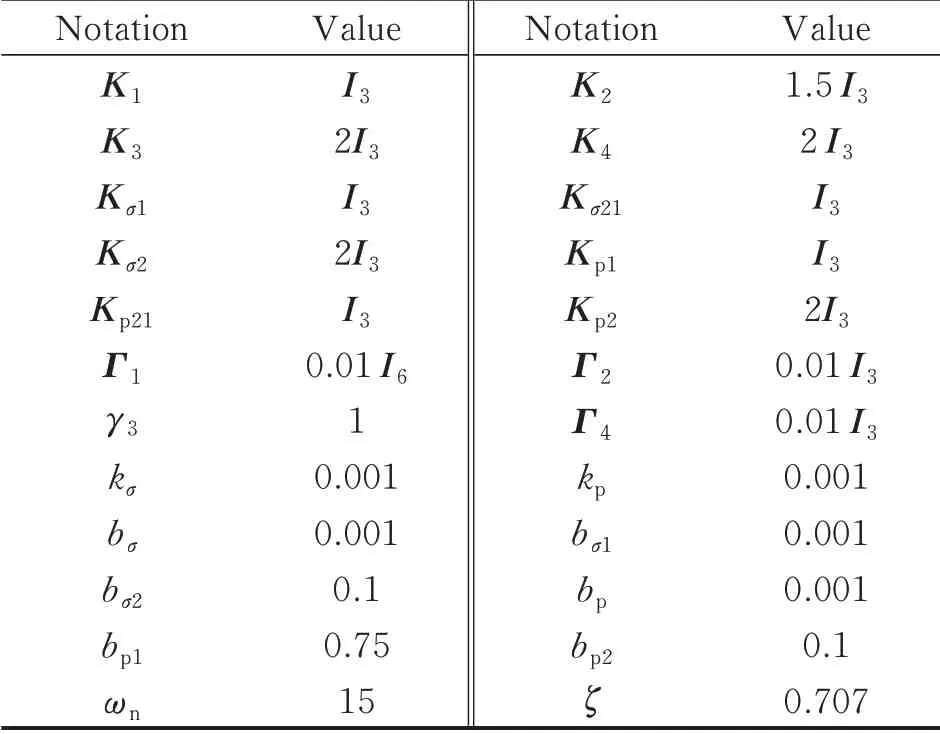
Table 1 Control,update and command filter parameters

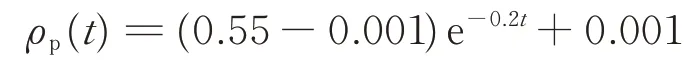
and

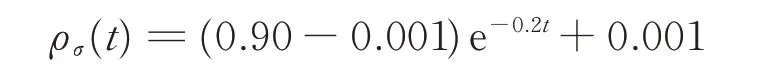
In order to show the effectiveness of the proposed control scheme，the following comparative simulations are carried out.

Case 1The control design with and without using the prescribed performance technique.

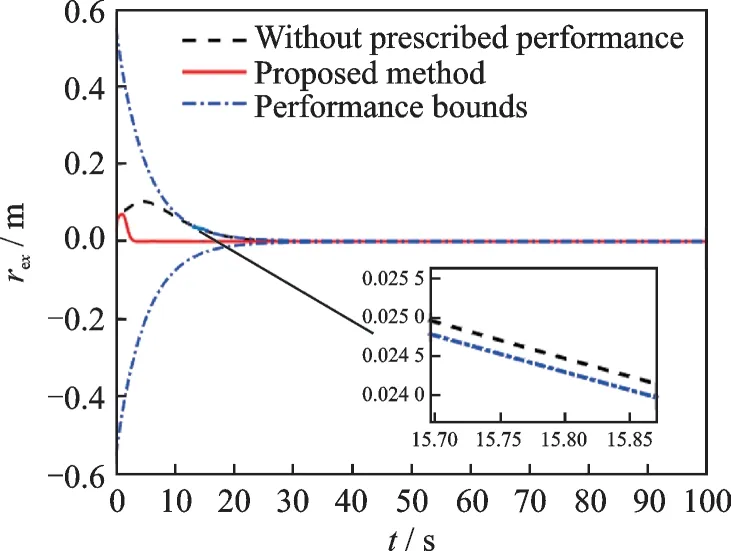
Fig.1 Relative position rex

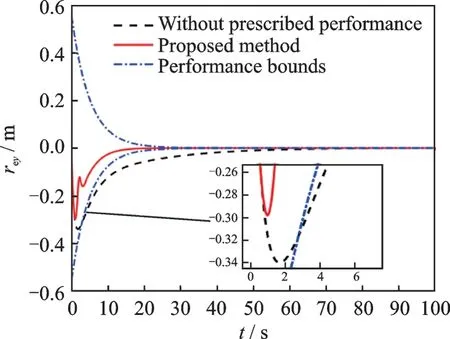
Fig.2 Relative position rey

Fig.3 Relative position rez

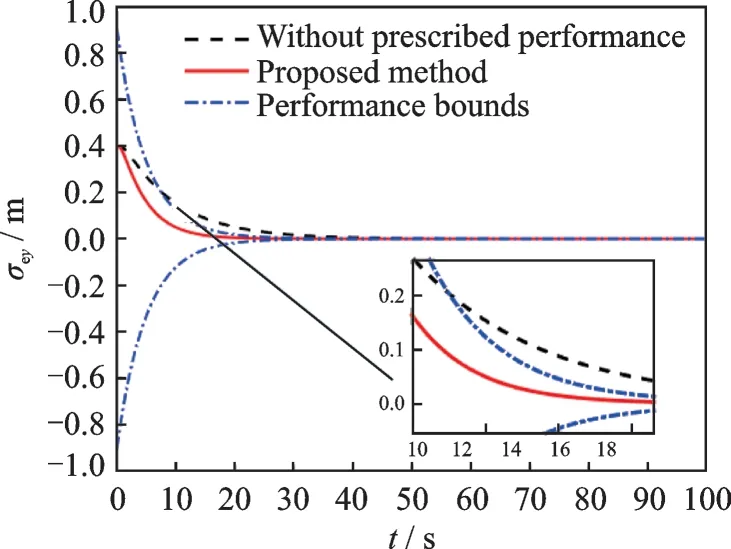
Fig.5 Relative attitude σey

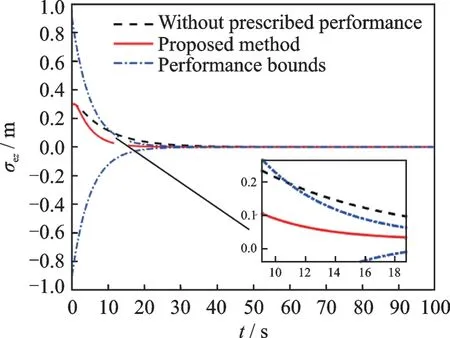
Fig.6 Relative attitude σez

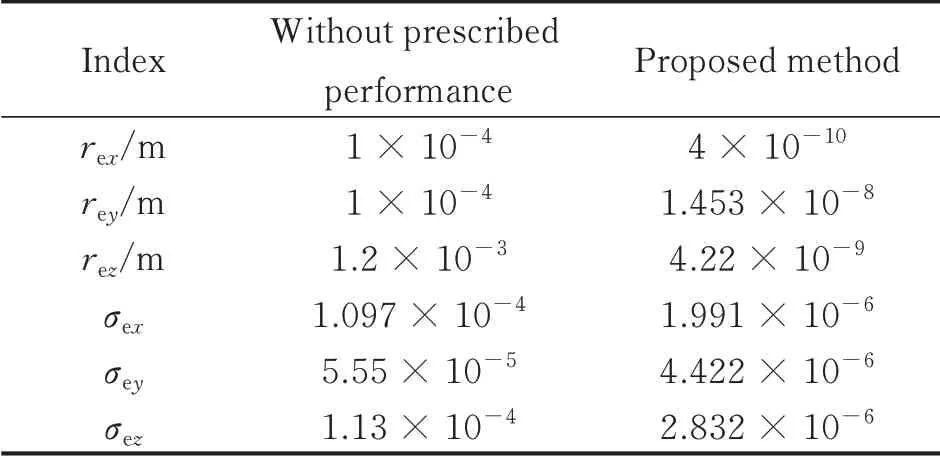
Table 2 Steady errors comparison

In order to give an fair comparison，all related gains and initial conditions are chosen exactly the same. The simulation results are demonstrated in Figs.1—6，and the steady errors of relative states are tabulated in Table 2. It can be clearly seen in Figs.1—6 that the time histories of the relative position and attitude obtained by the proposed method remain within the prescribed performance bounds for all time. However，the relative states for the case of without utilizing prescribed performance technique violate the predefined performance bounds and can not achieve the good performance of both transient error and steady error as this work.

Case 2The control design with and without considering the actuator saturation. Figs.7—12 show the comparison between control forces with saturation and without saturation constraints，and the comparison between control torques with saturation and without saturation constraints，respectively. It is demonstrated that the control forces and control torques for the scenario without considering the actuator saturation exceed the actuator magnitude constraints during the initial transient phase，while the actuator capacity constraints are never violated for the proposed method.

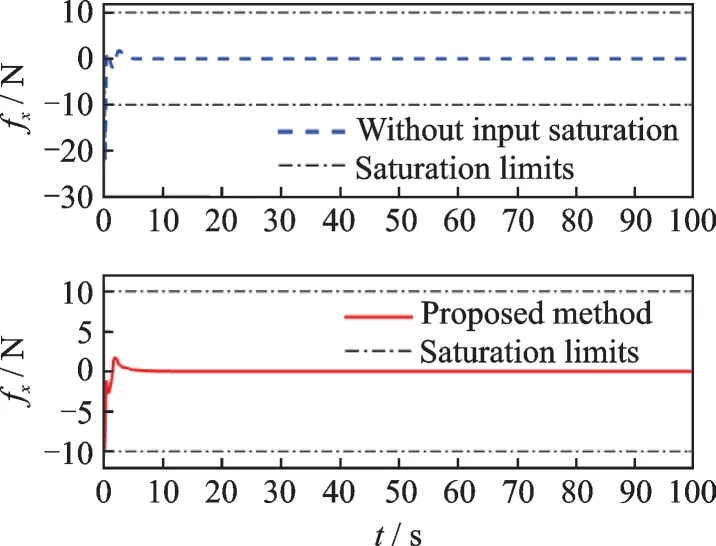
Fig.7 Control force fx

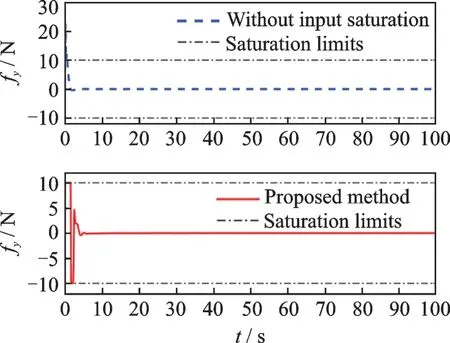
Fig.8 Control force fy

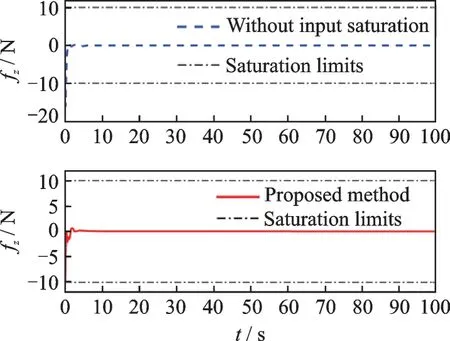
Fig.9 Control force fz

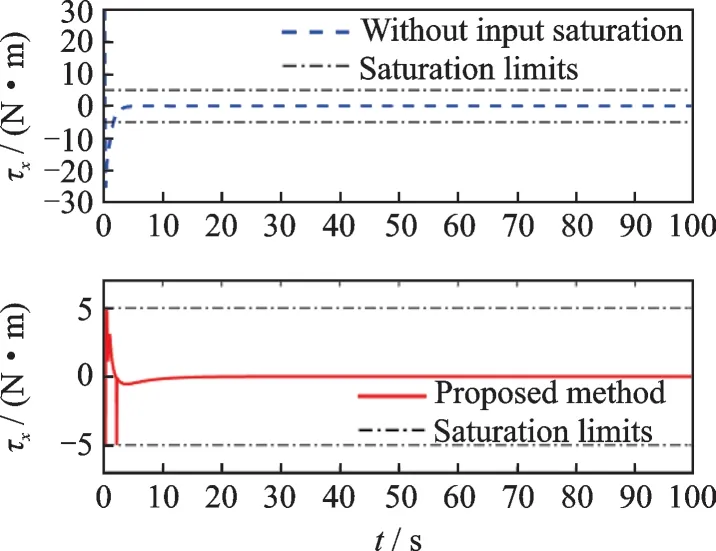
Fig.10 Control torque τx

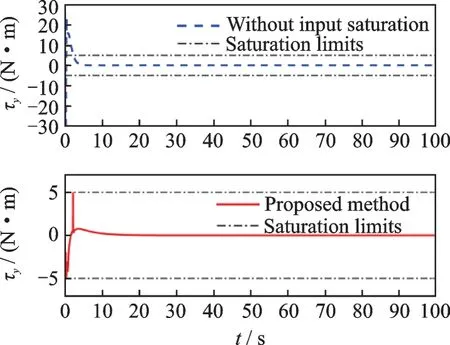
Fig.11 Control torque τy

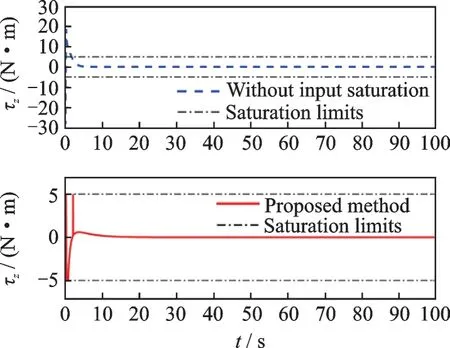
Fig.12 Control torque τz

4 Conclusions

A relative position and attitude control strategy with prescribed performance is proposed for dragfree satellite with cubic test mass in the presence of model uncertainty，external disturbance and actuator saturation. The prescribed performance control technique is utilized to ensure that the relative position and attitude control error remain within the required performance constraints. Then，the command filter is applied to avoid the arduous analytic computations of the time derivative of virtual controls，and a novel auxiliary system is designed to tackle the problem of actuator saturation. Comparative numerical simulations are finally conducted to demonstrate the effectiveness and superiority of the proposed control scheme.