复杂多针脚异型元件的视觉精密定位研究

(华南理工大学 机械与汽车工程学院, 广州 510640)

0 引言

PCB(printed circuit board)生产设备主要分为插件机和贴片机两种。插件机和贴片机分别涉及的技术为THT(through hole technology)和SMT(surface mounted technology)。异型插件机是将异型电子元件插装到PCB的自动化设备，其中采用的机器视觉定位是影响插装效果的核心技术[1]。

针对异形元件，本研究团队目前提出了基于旋转立体视觉的异型元件针脚定位方法[2]，该方法采用背光源照明，获取异型元件针脚不同角度的侧面图像，通过旋转立体视觉[3]重建元件针脚末端特征点在空间中的位置，能更稳定检测元件针脚的图像，获得更高的针脚定位精度。由于该方法拍照角度间隔为且是均匀分布的，所以对于针脚较多的元件，在某些拍照角度下元件针脚会相互遮挡，难以获得均分且间隔的针脚无遮挡拍摄角度。如果所获取的图像针脚互相遮挡，则难以提取准确的针脚末端特征点,如图1所示。

图1 针脚遮挡重叠图像

本文在上述研究的前提下，提出了求取针脚相互无遮挡拍摄角度区间的求取方法，解决针脚遮挡的问题。并且对于针脚数目较多的元件，无法获得均分无遮挡的均分拍照角度的情况，本文进一步提出一种多针脚异型元件精密定位方法。对于针脚数目繁多，无遮挡拍摄角度区间有限的情况，为得到更精确的定位精度，通过增加一些拍摄角度进行辅助定位。该方法同样采用旋转立体视觉定位系统获取异型元件针脚的侧面图像，然后提取图像各针脚末端边缘点，得到若干条(由于遮挡原因，提取的边缘点数量不定)反投影线，由不同角度的针脚图像获得的反投影线可以合成一个包络图，此包络图即为异形元件的针脚截面轮廓，基于此截面轮廓即可得到针脚纠偏数据。

上述针脚定位方法不直接提取单幅图像的针脚末端点，而是通过增加旋转成像次数，转而求取各幅图像针脚末端的亚像素边缘点，形成反投影线簇，间接得到针脚末端截面图像，进一步求取针脚末端中心点，有效避免了某些成像角度下针脚相互重叠的影响。所以该方法能对较多针脚的异型元件进行精确的定位。

1 无遮挡角度区间求取

图2 针脚无遮挡角度区间示意图

如图2所示，以两个针脚连线中心点O为远点，X轴与针脚连线重合，Y轴与针脚连线垂直，建立坐标系O-XOYO。求得在该坐标系下两针脚的两条内公切线方程，如式子(1)。其中d,D分别为针脚直径和两针脚间距。

(1)

如图1，以旋转轴心(圆心)为原点，以直线CP方向为Y轴建立坐标系C-XCYC,通过公式(2)的坐标系变换可得到XCY坐标系下的内公切线方程。

(2)

其中:a,b,c为原直线一般方程系数，R3×3为坐标系O-XoYo到坐标系C-XCYC坐标变换矩阵，可由3.2中系统标定得到，a′b′c′为转换后直线一般方程系数。

设转换后公切线方程为:

ax+by+c=0

(3)

成像相机旋转所得圆方程为:

x2+y2=l2

(4)

其中:l为相机光心与旋转轴的距离。

由式子(3)和式子(4)可求得内公切线与圆的交点坐标为:

(5)

设该公切线与圆的交点为如图1中的点t1和t2，则对应的角度为:

(6)

同理可求得θ3，θ4,则两针脚在该位姿状态下的无遮挡角度区间为:

u=[θ1，θ3]∪[θ2，θ4]

(7)

由于插件机的夹头和送料器的粗定位，元件抓取时会产生一定误差范围的偏移和旋转，误差为±e，如图3所示。

图3 粗定位误差示意图

由于圆半径l远大于误差e，故偏差对于元件旋转较为敏感，并且只需得到粗略的角度范围，考虑6种极限情况，如图4所示，分别求取6种极限情况下的无遮挡角度区间，最后取交集，则获得两针脚在粗定位后的无遮挡角度区间U。

图4 元件偏移极限

以此类推，对于多针脚元件，只要求取两两针脚无遮挡角度区间Ui，最后取其交集，即可到多针脚元件在旋转拍照过程中的无遮挡角度区间为:

(8)

在无遮挡角度区间选取合适的拍摄角度，即可获取无遮挡针脚图像。

对于针脚数目适中的元件，可采取本研究团队的文献[2]所述方法进行针脚精密定位，只需获得间隔的均分无遮挡拍照角度即可。但是当针脚数目达到一定数量时，有限的针脚无遮挡拍摄角度，难于获得均分的无遮挡拍摄角度，定位精度不够。下文将提出一种针脚数目较多的元件定位方法。

2 多针脚元件定位系统

如前文所述，对于针脚较多的元件，本文提出的定位方法不直接求取单幅图像的针脚末端点，转而求取各幅图像针脚末端的亚像素边缘点，形成反投影线簇，间接得到针脚末端截面图像，进一步求取针脚末端中心点，有效避免了某些成像角度下针脚相互重叠的影响。方法涉及旋转立体视觉的标定，亚像素边缘点和反投影线的求取。

2.1 旋转立体视觉

物体的重建是通过点的重建来实现的，因为点是空间中最基本的元素。把空间中物体的特征点重建出来后，物体的大致轮廓就能显示出来。当图像中的点通过反投影恢复空间中的点时，通过一个摄像机只能确定成像点在空间中的某根直线上，而不能确定点的确切位置，这根线即为反投影线。通过获取空间物体某一截面的侧面轮廓边缘点，进而构建出反投影线，通过不同角度相机得到反投影线簇，其包络线即为该物体某一截面的轮廓线，如图5。这就是本文基于旋转立体视觉的多针脚元件定位原理[4-6]。

图5 旋转立体视觉示意图

2.2 系统标定

文献[2]提出了较为成熟的内参标定和旋转轴标定方法，本文沿用该方法进行标定[7-8]。因为装配过程的误差，旋转轴与相机光轴不会正交，具有一定的偏斜，如图6，文献[2]的旋转轴标定方法通过平面拟合以及圆弧拟合的方法可以获得旋转轴向量n(nx,ny,nz)和光心旋转平面A,进而得到旋转轴与光心旋转平面交点的空间坐标OC(xc,yc,zc)。

图6 旋转轴

构建以点OC为坐标原点，旋转轴为Y轴，光心旋转平面为XOZ坐标平面的空间坐标系XCYCZC,如图7。然后通过公式的罗德里格斯变换[9]和矩阵变换原理得到坐标系OC-XCYCZC到初始位置相机坐标系O-XYZ的坐标变换矩阵R4×4。同理得到相机旋转前后的关系矩阵Mlr4×4[2]。

图7 构建坐标系

2.3 针脚末端亚像素边缘提取

根据前文标定得到的旋转轴向量n(nx,ny,nz，可得到相机光心绕旋转轴旋转后得到的平面方程A为:

nxX+nyY+nzZ=0

(9)

该平面与相机成像平面存在一条交线，如图8。相交直线方程为：

(10)

进一步得到该直线在图像坐标系的方程为：

nxβu+nyαv-nxβu0-nyαv0+nzαβ=0

(11)

其中α,β,u0,υ0均为标定所得相机内参。

图8 两平面交线示意图

目前亚像素边缘提取方法较为成熟，本文沿用文献[2]所提的空间矩不变方法提取亚像素边缘。为得到针脚图像在直线上的亚像素边缘点，本文通过迭代的方式，逐步得到所需边缘点坐标[10]。

3 反投影线求取

由前述方法得到针脚图像的亚像素边缘点如图9所示，每个边缘点对应一条反投影线，本文将通过相机成像模型求取该投影线。

图9 针脚亚像素边缘点

3.1 求取反投影线方程

根据相机成像模型[11]有式子(5):

(12)

其中:mij(i=1,2,3,j=1,2,3,4)由相机内参矩阵M1和外参矩阵M2相乘得到,内参矩阵可由标定过程直接获得。以初始位置相机坐标系为世界坐标系，前文所求相机关系矩阵Mlr4×4即为外参矩阵。公式(5)展开可以得到3个方程：

(13)

将公式(6)的第三个方程代入前两个方程，可以进一步消去Zc，得到：

(14)

式(7)为一个直线方程，假设前文得到的一个亚像素边缘点Pb在图像坐标系的像素坐标为Pb(ub,vb)，则根据式(7)可到该边缘点的反投影线方程为：

(15)

3.2 反投影线的坐标变换

前文所得各条反投影线方程是基于初始位置相机坐标系的，为得到基于2.2节构建的坐标系OC-XCYCZC的反投影方程，需要对直线方程进行坐标变换。公式(9)对直线进行坐标变换，得到转换后的直线方程系数。

(16)

基于坐标系OC-XCYCZC的反投影方程为：

(17)

由于所提取亚像素边缘点皆在前文所求交线L上，因此各边缘点形成的反投影直线簇都位于光心旋转平面上，形成平面直线簇，该直线簇可以得到平面包络图。

4 生成针脚末端截面包络图

由前文得到的反投影线簇可得到针脚末端截面包络图，进一步提取包络图中各针脚中心坐标，即可得到针脚的纠偏参数。

以光心旋转平面为虚拟成像平面，各投影线所形成的包络线围成的区域，将生成针脚末端截面包络图，将针脚截面区域灰度值置为0，其余像素点灰度值置为255，成像示意图如图10。 通过提高虚拟成像的像素点数，可以得到相对更高的定位精度。

图10 虚拟成像平面针脚成像示意图

采用上述方法得到二值针脚末端截面图像。该图像相当于元件各针脚被光心旋转平面所截的图像。 理想情况下，各条反投影线都和针脚柱面相切。对于圆形截面针脚，理想情况下得到的针脚末端截面包络图有一个最大内切圆，该圆即为针脚末端实际截面。所以，为提高针脚定位精度，本文将求取各针脚末端截面包络图的最大内切圆，并得到该圆的圆心坐标，如图11所示。

图11 针脚末端截面

提取间距最大的两个针脚的圆心C1(x1,y1),C2(x2,y2)。根据式(11)，即可得到针脚的纠偏参数。

(18)

5 实验与结果分析

本文采用异型元件插件机进行实验。采用背光源照明，映美精 DFK23G445 相机和 Computer-35 mm镜头进行元件图像采集，采集图像大小为像素,轴驱动电机采用Panasonic-MMMA3ACN1A 伺服电机，实验装置如图12所示。

图12 实验装置

为验证本文提出的基于多针脚电子元件的针脚定位方法，本文采用如图13所示电子元件为实验对象，该元件为dp15母头，具有双排共15针脚。

图13 dp15电子元件

为求得该元件无遮挡拍照区间，需得到该元件尺寸参数，如图14所示。下文实验精度分析，采用针脚横向间距l=2.77 mm为标准间距，e=k-1作为误差分析参数，其中k为本文所述方法所求针脚间距。

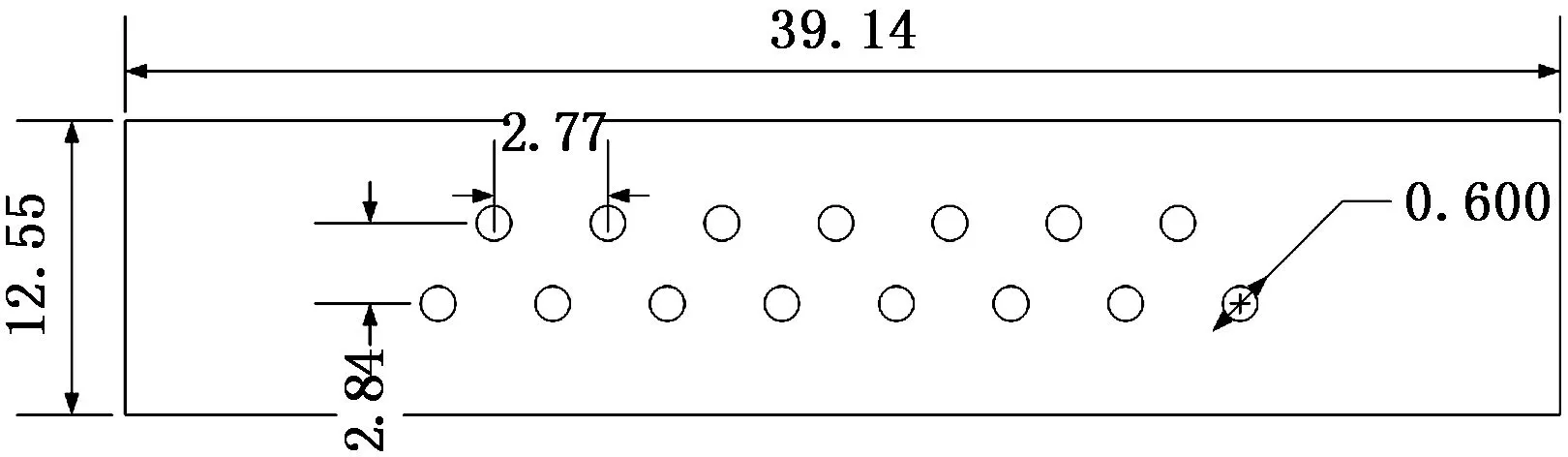
图14 元件模型

5.1 无遮挡拍照角度区间求取实验

由前文所述方法，求得无遮挡拍照角度区间如表1所示。

表1 元件无遮挡拍照角度区间 (°)

该元件在图所示实验装置下，共有6个无遮挡拍照角度区间，现于这6个区间内获得较为均匀的8个拍照角度分别为：48°、80°、100°、132°、226°、260°、280°、312°。

经过30次重复性夹取拍照实验，在上述八个拍照角度下，均未出现针脚相互重叠遮挡现象。可见本文提出的求取无遮挡拍摄角度方法，能够稳定可靠的获得无遮挡针脚图像。

5.2 定位精度实验

获得无遮挡针脚图像后，为验证本文所提出的定位方法的精度，将求得30次重复性实验的误差e=k-1的平均值和标准差，进行精度分析，结果如表2所示。

表2 针脚间距误差 (mm)

由结果可见，误差平均值与最大值均满足插件精度，且标准差较小，定位精度足够可靠和稳定。

5.3 效率分析

本文在配置为CPU i5-5200U 3.30 GHz、8 GB 内存的计算机上用C++验证本文方法计算效率。

因为插件机对元件针脚有粗定位，虚拟平面上生成的针脚截面区域只会形成在一定像素范围内，通过选取合适的像素区域，可大幅缩短形成包络图和内接圆的耗时。本文采用优化后的程序对该实验元件进行30次重复实验，得到各元件平均定位耗时。

表3 定位效率 (ms)

结果如表3所示，提取每幅图像针脚亚像素边缘点的速度较快，平均耗时仅需6.834 ms,形成针脚包络图耗时较多，占据大部分计算时间，经过优化像素搜索区域，平均耗时为83.235 ms。定位方法平均总耗时为143.191 ms，由文献[2]可知，传统底部拍照定位方法需要将原件移至底部相机上方进行拍照，该动作耗时为300～400 ms。本文所提方法无需该动作，减少了这部分时间，所以插件总时间符合插件机插件要求。

6 结论

本文提出了一种多针脚异型元件的定位方法，并提出了初步求取元件针脚无遮挡拍照角度的方法，搭建了旋转立体视觉实验装置，进行针脚定位实验分析。实验表明，本文所提出的定位方法，对于多针脚异型元件具有良好的定位可靠性和稳定性，定位精度和效率均满足插件要求。后续会对更多复杂多针脚元件进行实验和分析，完善该定位方法。