激光质谱中基于数据挖掘的激光输出功率预测技术研究

刘莲花1,杨文喜,张晓卫1,但勇军,刘 彬

(1.粒子输运与富集技术国防重点实验室，天津 300180；2.核工业理化工程研究院,天津 300180)

0 引言

预测是定期更新对未来数据的当前观察，以反映新的或变化中的信息过程。它是基于分析当前和历史数据来决定未来趋势的过程。预测分析是一种统计或数据挖掘解决方案,包含可在结构化和非结构化数据中使用以确定未来结果的算法和技术。可为预测、优化、预报和模拟等许多其他用途而部署，也可为规划流程提供各种信息，并对未来提供关键洞察[1]。

数据挖掘主要应用于描述类及预测类工作。其适用的关键在于两个方面：一方面数据之间确实存在一定关系；另一个方面需要大量数据。通过定性分析，已经确定了参数的关系确实存在，通过数据库技术，为系统参数积累了大量的真实历史数据，因此开展数据挖掘技术研究条件基本满足[2]。

由于激光质谱系统逻辑结构复杂多样，激光质谱系统包括激光系统、质谱装置、质谱信号测量装置、温湿度仪表、压力仪表等设备，激光质谱系统运行状态受到激光系统、质谱装置、质谱测量装置、激光器特性参数以及环境参数的影响，同时激光质谱系统内的多种设备在运行期间相互影响。激光输出功率对激光质谱系统的运行状态影响比较大，对激光输出功率的合理预测，做到提前掌握激光系统未来状态的发展趋势，为激光质谱系统运行决策提供重要依据，因此，进行激光输出功率预测技术研究对整个激光质谱系统具有很重要的意义。

由于激光系统的物理过程相对较为复杂，目前，还未建立完整的物理仿真模型，因此激光输出功率与其他参数关系的描述还没有。因此采用数据挖掘方法模拟关系模型，体现所有可能的影响因素，进而实现对激光输出功率的准确预测。

1 激光质谱系统结构及激光输出功率预测原理

激光质谱系统由激光系统、质谱装置、质谱信号测量装置及辅助供水系统等设备组成。激光质谱系统具有复杂的物理逻辑关系和工艺结构，并且相互关联，相互影响，任何环节的变化都会影响质谱系统的运行状态。激光质谱系统的运行状态由多个参数表征，包括激光系统特性参数、质谱信号参数及环境参数等，任何一个参数出现异常都会标志着整个系统状态出现异常，而激光系统是激光质谱系统运行的前提条件，因此对激光系统运行状态的提前掌握对质谱系统运行具有重要意义。激光系统参数包括激光功率、脉冲延时、光束质量、光斑大小和形状等参数，而激光功率是激光系统运行状态的关键参数，因此，试验期间，需要实时预测激光输出功率的未来发展趋势，发现可能影响激光系统运行状态的因素，提前解决潜在问题，为质谱系统的稳定运行提供保障。

激光输出功率预测结构如图1所示，激光数据采集系统实时采集激光输出功率、脉冲延时、光斑等实时监测数据，将实时数据存储到历史数据库中，同时将实时数据发送给预测模块。预测系统读取历史数据库中历史数据建立预测模型，根据实时数据对输出功率进行实时预测。

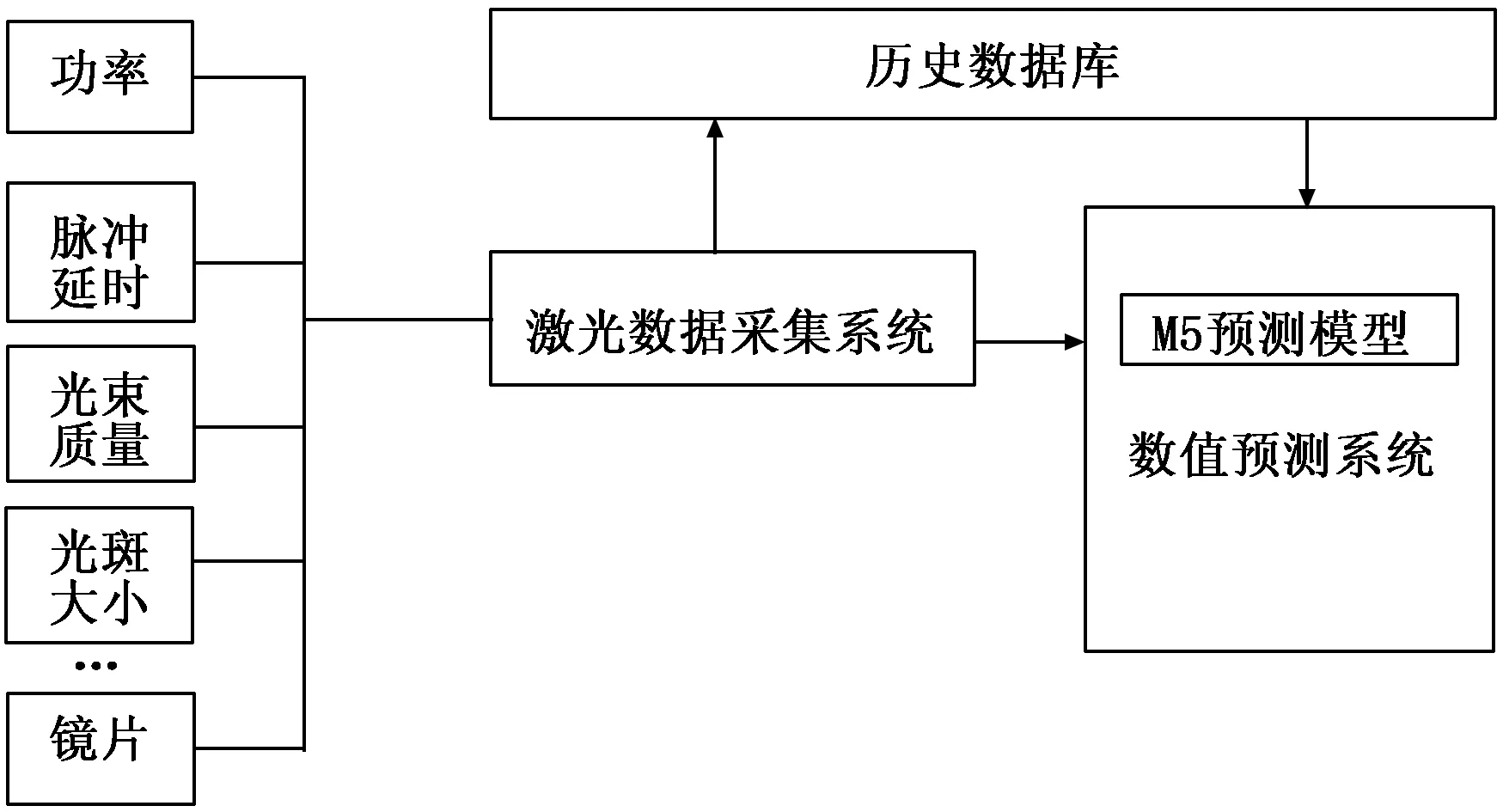
图1 预测系统结构图

2 数据处理

数据样本是数据预测模型及相关技术的研究的关键因素，也是模型选定和验证的根源，因此数据格式及数据的正确性具有确定性作用。

2.1 时间对齐

由于激光数据采集系统需要实时采集不同独立运行的多个设备的多个数据，数据采集及存储的时间不是完全的相同，因此需要对历史数据进行相应的处理才能作为数据学习样本。将一分钟均分为12份，即5秒钟为一个时间段，一个时间段内的所有数据进行平均后进行保存，如果在该时间段内没有数值则以上一个时间段内的数值作为该时间段内的数值进行保存，从而实现数据的时间一致性。

2.2 异常数据判断

激光系统在运行过程中，功率输出会受到多种因素的影响，会出现异常数据，同时会自行恢复正常状态，这样的异常数据无法预测，因此在预测过程中需要将异常数据进行剔除。采用两种方式进行数据的优化处理，分别为正态分布的3σ原则和参考在网络传输信号中的通信延时的计算方式RTT。

3σ原则以数据符合正态分布为参考，每次当有新的捕获数据值时，通过已有数据计算得到的均值μ和方差σ得到3σ的范围，基本涵盖99.74%的数据分布，当超出3σ范围的数据值，则按异常值进行处理。

RTT计算方式中每一次捕获到的数据值为RTT，SRTT是用于计算RTO的部分的参数值(性质上类似于均值)，DevRTT同样是用于计算RTO部分的均值(类似于方差)，最后计算RTO。

RTO=μ*SRTT+/-δ*DevRTT

(1)

通过(1)式计算RTO得到一个符合条件的数据范围，再通过比对新捕获的数据值与已有的数据范围之间的关系判断捕获的数据是否为异常值。

3 数据预测建模

预测型数据挖掘大体可分为分类和回归，回归一般包括线性回归和非线性回归，许多非线性回归都可以经过适当的变化转化为线性回归。

采用激光系统历史数据作为样本数据，对几种预测模型进行测试研究，从而确定所选取的模型。

3.1 M5模型树算法

M5模型树算法是一种回归树算法。它结合了传统的决策树的理念，并且有一定的概率在叶子结点处生成线性回归函数。模型树的生成和决策树的生成是十分地类似。

M5模型树算法即为输入空间X1、X2被分到各个区域上，独立的回归模型能分别产生于这些区域中。在生成模型树时，一个特征首先被放置在根节点，并为每一个可能的数值生成一个树枝；然后根结点的样本集被划分为几个子集，每一个树枝下有一个子集。这个过程被不断重复，直至某一个结点下的所有样本拥有相同的分类时，那一个部分的生成过程方才停止。这个被选择来划分特定的样本集的特征，是通过叫做“划分准则”的统计学特性来决定的。对于普通的决策树来说，划分准则是要尽可能地减少产生的子集中的熵值，即尽可能多地把同一类的样本划分在一个子集中。而M5模型树是一个数值预测算法，它的划分准则是基于某一个结点下的所有数值的标准差来决定的。这个标准差被用作该结点的误差度量，而能够减少最多误差值的特征就被选择为该结点的划分。划分过程在某一结点的数值标准差很小时停止，或者在某一个子集中只剩下很少的样本时停止[3]。线性回归模型于划分停止后在每个终止结点上生成。

根据M5模型的算法原理，采用激光系统输出功率作为预测目标，根据影响激光输出功率的影响因素生成的模型树如图2所示。

图2 M5模型树

采用激光系统某一段时间的历史数据作为样本数据在M5算法模型上进行了测试，激光输出功率的历史预测结果与历史真实值对比结果如图3所示，此段时间内，历史真实值与历史预测值偏差不大。

图3 M5模型预测结果

3.2 多层感知机模型

多层感知机由多层神经元组成。输入的信号被提交到隐藏层的神经元中。在使用多个隐藏层时，每一层的输出都被作为输入提交到下一层神经元中。按照标准的回归模型，每一个神经元使用一个非线性激励函数：

(2)

多层感知机模型的理念是：激励函数概略地体现了一个真实神经元的激励作用。最高层隐藏层神经元的输出被提交到输出层。只有一层隐藏层神经元配合以下函数使用[4]：

(3)

(4)

式(4)中，c是放缩参数使得多层感知机的输出拟合数据。

在隐藏层使用传统的sigmoid函数：

(5)

而感知机的权重则通常由梯度下降最小化算法来得出。

采用激光系统历史数据作为样本数据，预测某一特征值X1按照如下过程：输入的特征值X1生成一些滞后特征，再使用这些特征构造多层感知机模型，如图4所示。

图4 多层感知机预测模型

同样采用激光系统某一段时间的历史数据作为样本数据在多层感知机算法模型上进行了测试，激光输出功率的历史预测结果与历史真实值对比结果如图5所示，此段时间内，历史真实值与历史预测值偏差比较大。

图5 多层感知机预测结果

3.3 线性回归

在统计学中，线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计[6]。

给定一个随机样本(Yi,Xi1,Xi2,…,Xip)，i=1,…,n,一个线性回归模型假设回归子Yi和回归量Xi1,Xi2,…,Xip之间的关系是除了X的影响外，还有其他的变数存在。加入一个误差项εi(也是一个随机变量)来捕获除了Xi1,Xi2,…,Xip之外任何对Yi的影响[7]。所以一个多变量线性回归模型表示为以下的形式：

偷偷拿走我的画的人是秦晴，因为他也有和我一样的爱好，却只能背着爸妈进行。爸妈发现后，一怒之下将其“毁尸灭迹”。

Yi=β0+β1Xi1+β2Xi2+…+βpXip+εi,i=1,…,n

(6)

采用激光系统样本数据，预测某一特征值X1按照如下过程：输入的特征值X1生成一些人造的时间戳，并生成一些滞后特征， 根据数据生成线性回归模型。

采用激光系统同一段时间的历史数据作为样本数据在线性回归算法模型上进行了测试，激光输出功率的历史预测结果与历史真实值对比结果如图6所示，此段时间内，历史真实值与历史预测值偏差非常小。

图6 线性回归预测结果

3.4 支持向量机

支持向量机使用线性模型，通过一些非线性映射输入向量x到高纬度特征空间，从而生成非线性分类边界。一个在此新空间生成的线性模型可以代表一个原空间的非线性决策边界。在新的空间里，一个最优的分隔超平面被建立。这一最大间隔超平面给出了决策集之间的最大间隔。靠这个最大间隔超平面最近的训练样本被称为支持向量。所有其他的训练样本都和决定这个二元分类边界无关[8]。

在线性可分的数据中，一个拥有3个特征的分隔二元决策集的超平面可以由以下方程表示：

y=ω0+ω1x1+ω2x2+ω3x3

(7)

在式(7)中，y是输出，xi是特征值，而且有四个需要算法学习的权重ωi。这些权重ωi就是决定超平面的参数[9]。这个最大间隔超平面可以被支持向量由以下方程表示：

y=b+∑αiyix(i)·x

(8)

在线性不可分的数据中，一个高纬度版本的方程简单地如下表示：

y=b+∑αiyiK(x(i),x)

(9)

在式(9)中，函数K(x(i),x)被定义为核函数。常见的核函数有多项式核函数等。

采用激光系统样本数据，预测某一特征值X1按照如下过程：输入的特征值X1生成一些滞后特征， 经计算后获得支持向量机模型及权重值。

通过支持向量机模型，计算激光输出功率的历史数据预测值。

4 结果分析

根据激光质谱实验实际情况，在不同季节以及一天的不同时段实验结果略有不同，因此采用激光质谱系统多次实验的激光系统功率及相关历史数据进行了历史预测测试。通过选择三次试验的7个不同时间段数据，选择每个时间段为30分钟，进行预测10分钟内的数据，将预测的历史数据与真实历史数据进行比较，并计算平均误差。通过对已经建立的支持向量机预测模型、线性回归模型、M5模型和多层感知机模型分别进行多个时间段数据的训练、预测和平均误差计算，结果如表1所示。在7个时间段内，支持向量机模型和多层感知机模型给出的预测结果的平均误差都大于线性回归模型和M5模型。根据激光系统的功率数据特性，预测误差应小于1。M5模型在其中的4个时间段内的平均误差小于1，其中3个时间段的误差比较大。经过与激光系统的实际运行状态进行了分析与对比，其中3个误差比较大的时间段为系统调节或故障阶段，数据波动较大，预测偏差较大，因此M5预测模型的预测结果更接近激光系统输出功率的历史数据。

同时又对4种预测模型的预测误差的平均值和方差进行了计算，结果如图7所示。其中支持向量机模型的误差的平均值和方差为40.59和92.02，远远超过了线性回归模型、M5模型和多层感知机模型，线性回归模型和M5模型的误差平均值和方差相差不多，与误差结果基本一致。由于M5模型在预测精度和稳定性上都为最优选择，因此选择M5模型作为激光输出功率的研究预测模型。

表1 预测模型误差比较

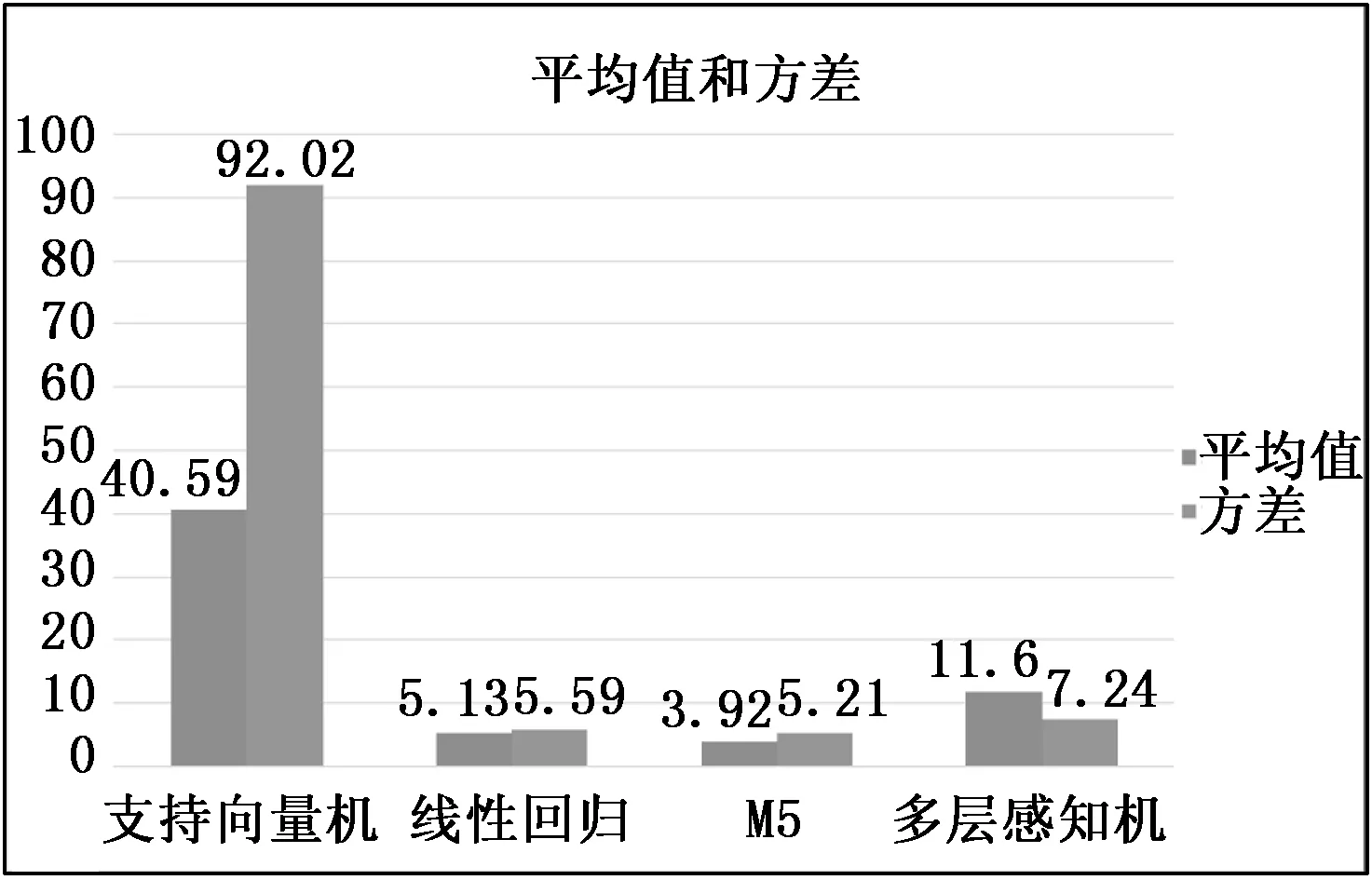
图7 模型的平均值和方差

5 结论

根据激光系统的部分历史数据分别对M5预测模型、线性回归模型、向量机模型进行了建模及预测分析，通过比较几个预测模型在不同时段间的预测误差、平均误差及方差结果，M5预测模型的预测结果相对最优。模型分析结果表明，M5预测模型适合进行质谱系统激光输出功率的预测技术研究。