TORA系统基于自调节滑模干扰补偿器的解耦滑模控制

于 涛,王益博,赵 伟2,杨 昆

(1.辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001；2.北京印刷学院 信息工程学院，北京 102600)

0 引言

具有旋转激励的平移振荡器(Translational Oscillators with Rotating Actuator，TORA)是一种典型的欠驱动系统，该系统由非驱动的移动小车和直接驱动的旋转小球构成。TORA系统最初作为简化模型用于研究双自旋航天器的共振问题， 目前作为非线性基准系统用于验证欠驱动系统非线性控制设计的有效性[1-3]。TORA系统的欠驱动特性使得实现其有效控制具有一定的挑战性，因而其控制问题日益受到控制领域研究人员的关注。

目前，国内外研究人员已经对欠驱动TORA系统的控制问题开展了很多研究工作。文献[4]基于耗散理论设计了一种增强耦合型控制器，实现了欠驱动TORA系统的有效镇定控制。文献[5]提出了一种非线性连续控制方法，可实现TORA系统的全局镇定控制。文献[6]针对TORA系统设计了一种基于递推反步法的非线性控制器，该控制器具有很好的镇定控制性能。文献[7]提出了一种基于自适应神经网络的输出反馈控制方法，可实现欠驱动TORA系统的快速镇定控制。此外，滑模控制[8]、自适应控制[9]和约束控制[10]在欠驱动TORA系统的稳定控制中也有一定的应用，并且已经取得了很好的控制效果。

针对欠驱动TORA系统，本文提出一种基于自调节滑模干扰补偿器的解耦滑模控制方法。所提出的控制方法不需要获得系统不确定性上界的先验知识，对于系统不确定性具有良好的适应性和鲁棒性。首先定义TORA系统的两级滑模面，然后基于第二级滑模面设计自调节滑模干扰补偿器。为抑制控制器的高频抖动并提高系统状态的趋近速度，设计了一种新型的双幂次趋近律。最后基于所设计的自调节滑模干扰补偿器和第二级滑模面，利用新型的双幂次趋近律推导解耦滑模控制律。

1 TORA系统的动力学模型

欠驱动TORA系统的结构如图1所示，该系统由通过刚度系数为k的弹簧与固定墙面相连的移动小车和通过长度为r的无质量刚性连杆悬挂于移动小车内的旋转小球构成。质量为M的移动小车在垂直平面内横向移动，移动小车的水平位移为x。质量为m的旋转小球在驱动力矩τ的作用下在垂直平面内转动，旋转小球相对球心轴的转动惯量为I，旋转小球相对重力方向的转动角度为θ。

图1 欠驱动TORA系统的结构

根据欧拉-拉格朗日动力学方程，TORA系统的动力学模型可以表示为:

(1)

式中,τf(t) =[τf 1(t)τf 2(t)]T为未知有界的包含外部扰动和建模误差的系统不确定项，各向量和各矩阵的表达式分别为:

式中,g为重力加速度。

由式(1)可见，TORA系统是一个具有2个位形变量和1个驱动输入的欠驱动系统。

将欠驱动TORA系统的动力学模型式(1)表示为如下形式:

(2)

式中,

[g1(θ)g2(θ)]T=M-1(q)E

[f1(t)f2(t)]T=M-1(q)τf(t)

注1：由系统不确定项τf(t)的有界性和惯性矩阵M(q)的正定性及其各元素的有界性，可以验证不确定性f1(t)和f2(t)也是有界的，即有如下关系成立:

|f1(t)|≤κ1|f2(t)|≤κ2

(3)

式中,κ1和κ2为未知的正常数。

2 基于干扰补偿器的解耦滑模控制

2.1 系统各级滑模面设计

(4)

式中,c1为正常数。

(5)

式中,c2为正常数。

由于整个系统只有1个驱动输入，为同时保证移动小车子系统的第一级滑模面s1(t)和旋转小球子系统的第一级滑模面s2(t)的收敛性，利用移动小车子系统的第一级滑模面s1(t)设计一个双曲正切函数型中间变量z(t)为:

(6)

式中,λ1和λ2为正常数。

将中间变量z(t)并入旋转小球子系统的第一级滑模面s2(t)中，设计TORA系统的第二级滑模面S(t)为:

(7)

2.2 自调节滑模干扰补偿器设计

(8)

式中，双曲正割函数sech(λ2s1)的表达式如下所示：

对式(7)求导，由式(2)和式(8)可以得到：

(9)

由式(2)、式(4)和式(9)，进一步可得:

(10)

式中,

F(t)=f2(t)-c2β(s1)f1(t)

注2：由式(8)可见0<β(s1)≤λ1λ2，因此β(s1)有界。进而由式(3)可知，系统不确定性F(t)也是有界的。不妨设系统不确定性F(t)的上界为未知的正常数K，即|F(t)|≤K。

由于欠驱动TORA系统中存在着不确定性，为降低不确定性对系统性能的不良影响并提高系统的控制精度，设计自调节滑模干扰补偿器逼近系统不确定性F(t)。自调节滑模干扰补偿器的具体形式为：

(11)

u(t)=εσ+ρ(t)sign(σ)

(12)

式中,ε为正常数；切换增益ρ(t)的自适应律为:

(13)

式中,η和ρ(0)为正常数。

证明：定义备选Lyapunov函数V1(t)为:

(14)

由式(10)和式(11)，可以得到:

(15)

对式(14)求导，并由式(13)和式(15)可得:

σ·(F-u)+|σ|(ρ-K)

(16)

注意到|F(t)|≤K，由式(12)进一步可得:

(17)

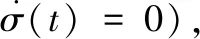
u(t)=εσ+ρ(t)tanh(λ3σ)

(18)

式中,λ3为正常数；双曲正切函数tanh(λ3σ)的定义如式(6)所示。

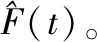
2.2 基于新型双幂次趋近律的解耦滑模控制器设计

为保证系统状态的快速趋近并抑制控制器的高频抖动，本文在文献[11]设计的双幂次趋近律基础上提出一种新型的双幂次趋近律，然后在此基础上设计基于自调节滑模干扰补偿器的解耦滑模控制律。

本文设计的新型双幂次趋近律为:

k3tanh(λ4S)

(19)

式中,k1，k2，k3和λ4为正常数；γ为小于1的正常数。在趋近律式(19)中，当系统状态远离滑动模态(|S|>1)时，指数趋近项-k1|S|1+γsign(S)起主要的趋近作用；当系统状态接近滑动模态(|S|<1)时，指数趋近项-k2|S|1-γsign(S)起主要的趋近作用；趋近项-k3tanh(λ4S)是等速趋近项-k3sign(S)的连续逼近，用以进一步加快系统状态的趋近速度。

注4：可以看出，若不计参数ki对于趋近作用大小的影响，当系统状态接近滑动模态(|S|<1)时，指数趋近项-k2|S|1-γsign(S)的趋近作用不及等速趋近项-k3sign(S)。趋近项-k3tanh(λ4S)作为等速趋近项-k3sign(S)的连续逼近，适当地增大其参数λ4有利于加速系统状态的趋近过程。

(20)

由式(19)和式(20)，可得解耦滑模控制律τ(t)为:

τ(t)=

(21)

证明：定义备选Lyapunov函数V2(t)为：

(22)

将解耦滑模控制律式(21)代入式(10)，可以得到:

(23)

(24)

由式(24)，进一步可得:

(25)

如果k2|S|1-γ≥δ，则由式(25)可得:

(26)

由式(24)，又可以得到:

(27)

如果k1|S|1+γ≥δ，则由式(27)可得:

(28)

综上可见，第二级滑模面S(t)能够在有限时间内收敛至零邻域:

(29)

因此，在辅助滑模面σ(t)的收敛时刻前第二级滑模面S(t)是有界的。

定理3：对于式(2)所示的欠驱动TORA系统，按式(4)、式(5)和式(7)分别设计各级滑模面，并按式(11)至式(13)设计自调节滑模干扰补偿器，如果采用式(21)所示的解耦滑模控制律，那么第一级滑模面s1(t)和s2(t)渐近收敛于零。

对于分别按式(4)、式(5)和式(7)设计的各级滑模面，借助文献[12]定理2的证明可以证得，采用式(21)所示的解耦滑模控制律，能够确保第一级滑模面s1(t)和s2(t)渐近收敛于零，即：

(30)

3 仿真实验验证

为验证本文解耦滑模控制方法的有效性，利用Matlab数值仿真环境进行欠驱动TORA系统的镇定控制实验。数值仿真实验中，欠驱动TORA系统的各参数分别取为[1]：M=1.3608 kg，m=0.096 kg，k=186.3 N/m，r=0.0592 m，I=2.175×10-4kg·m2。

3.1 基于精确模型信息的控制性能检验实验

首先，检验本文解耦滑模控制器的控制性能。为验证本文解耦滑模控制器具有较好的控制性能，与传统解耦滑模控制器进行对比分析。传统解耦滑模控制器的具体形式为:

(31)

在式(31)中，各参数的选取范围、各变量和各滑模面的定义与本文解耦滑模控制器式(21)相同。

在基于精确模型信息的控制性能检验实验中，设移动小车子系统和旋转小球子系统的不确定性f1(t)=f2(t)=0。需要说明的是，此时本文解耦滑模控制器式(21)仍采用自调节滑模干扰补偿器对系统不确定性F(t)进行观测。

在进行控制性能对比时，本文解耦滑模控制器的各参数分别取为：c1=8.8，c2=1.5，λ1=6.9，λ2=6.5，ε=2.4，η=0.6，ρ(0)=1.1，λ3=6.7，k1=4.4，k2=3.4，k3=4.9，γ=0.5，λ4=6.7。传统解耦滑模控制器的各参数分别取为：c1=8.5，c2=1.1，λ1=7.1，λ2=6.2，k1=1.9，k2=5.3。

图2和图3分别给出了本文解耦滑模控制器和传统解耦滑模控制器的仿真实验结果。由图2和图3可以看出，两种解耦滑模控制器都能有效实现欠驱动TORA系统的镇定控制。进一步对比图2和图3可见，在本文解耦滑模控制器的作用下闭环控制系统具有更好的动态过程，本文解耦滑模控制方法能够更好地实现欠驱动TORA系统的快速镇定控制。具体而言，在本文解耦滑模控制器式(21)的作用下闭环控制系统的镇定时间为7.1 s，在传统解耦滑模控制器式(31)的作用下闭环控制系统的镇定时间为8.4 s。不仅如此，通过仿真对比还可以看出，本文解耦滑模控制器的能耗也明显低于传统解耦滑模控制器。

图2 本文解耦滑模控制器的仿真实验结果

图3 传统解耦滑模控制器的仿真实验结果

3.2 鲁棒性检验实验

然后，检验本文解耦滑模控制器的鲁棒性。为此，在欠驱动TORA系统的各标称模型参数中人为地添加±10%的不确定性。需要说明的是，此时本文解耦滑模控制方法仍采用标称模型参数设计解耦滑模控制律。在鲁棒性检验实验中，本文解耦滑模控制器的各参数和欠驱动TORA系统的初始条件与基于精确模型信息的控制性能检验实验相同。

图4和图5给出了本文解耦滑模控制器的鲁棒性检验结果。由图4和图5可以看出，闭环系统的控制性能没有受到其内部参数变化的影响，移动小车的水平位移x(t)和旋转小球的转动角度θ(t)仍能快速地收敛至零。鲁棒性检验结果表明，本文解耦滑模控制器对于系统不确定性具有良好的鲁棒性和适应性。

图4 本文控制器的鲁棒性检验结果(+10%参数不确定性)

图5 本文控制器的鲁棒性检验结果(-10%参数不确定性)

4 结论

本文对欠驱动TORA系统的镇定问题进行了研究，提出了一种基于自调节滑模干扰补偿器的解耦滑模控制方案。所提出的控制方案能够有效实现欠驱动TORA系统的快速镇定控制，并且对于系统的不确定性具有良好的鲁棒性和适应性。所提出的控制方案包括设计一种自调节滑模干扰补偿器和一种新型双幂次趋近律。所设计的自调节滑模干扰补偿器不需要预知系统不确定性的上界信息，能够对系统的不确定性进行准确估计。所提出的新型双幂次趋近律不仅可以保证系统状态的快速趋近，并且能够保持解耦滑模控制的连续性。采用Lyapunov稳定性理论证明了闭环控制系统的稳定性，并且通过数值仿真实验验证了所提出的控制方案的有效性。