翼身融合布局飞机机体-发动机气动干扰效应
2019-09-25周翰玮陈勇谭兆光司江涛李杰李栋
周翰玮,陈勇,*,谭兆光,司江涛,李杰,李栋
1. 中国商用飞机有限责任公司 上海飞机设计研究院,上海 201210 2. 西北工业大学 航空学院,西安 710072
翼身融合(BWB)布局飞机是一种新型布局的运输机。由于其高度的集成特性,其浸润面积也大大小于同量级的传统布局飞机,因此,与同量级传统布局的飞机相比,BWB布局飞机具有较轻的重量、更高的升阻比和更小的燃油消耗量。除上述优势外,BWB布局飞机还具有其他更好的特性,比如更好的舒适性等[1]。欧美等航空工业发达地区相继投入大量资源进行BWB研究[2-3],美国以波音公司为首携同Langley研究中心以及斯坦福大学等科研机构对BWB进行了广泛而深入的研究,涉及气动设计[4-5]、结构分析与客舱设计[6-7]、风洞试验[8]、操稳特性评估[9]等。中国相关高校和科研机构也针对BWB布局飞机进行了探索和研究[10-13],西北工业大学张彬乾等已针对BWB布局总体方案、气动设计、飞行控制等多个领域开展了研究工作[14-15]。
然而由于总体布局、适航、噪声等方面的限制,BWB布局飞机不能像传统布局飞机采用翼吊或者在机身上安装发动机,因此在背部安装发动机成为首选,将发动机布置在BWB布局飞机背部,能够有效减小发动机短舱对飞机翼面流场的干扰和破坏,显著提升飞机的气动性能。但背部安装发动机容易带来一系列的空气动力干扰问题,其发动机与机体之间的干扰和影响机制与常规布局飞机不同。发动机与机身一体化的气动设计已成为BWB发展的关键领域。本文针对BWB布局飞机的机体和发动机之间的气动干扰进行了数值研究,主要包括喷流短舱及通流短舱的影响,以及短舱高度、展向位置、弦向位置等位置参数影响。
1 计算方法概述
1.1 控制方程与离散格式
本文控制方程为三维积分形式的雷诺平均Navier-Stokes方程[16],其表达式为
(1)
式中:v为控制体体积;s为控制体表面;Q为守恒量;fiv为对流项;fvs为黏性通量;n为单元表面的外法向单位矢量。控制方程采用有限体方法进行离散,时间推进采用LU-SGS(Lower Upper-Symmetric Gauss Seidel)方法,空间离散采用Roe’s FDS格式,高阶重构采用三阶MUSCL格式,为了抑制激波振荡采用van Albada限制器,湍流计算采用了两方程k-ωSST(Shear Stress Transport)湍流模式[17]。
1.2 涡轮风扇发动机计算模型
涡轮风扇发动机流动特性非常复杂。但是由于发动机对飞机部件的干扰主要是体现在进排气效应上,而发动机内部流场并不是主要关注点,因此利用特定的计算边界条件对其进排气流场进行模拟就能够实现整个干扰流场的模拟。对于一个典型的涡轮风扇发动机,其计算模型可简化为如图1 所示[18-19]。
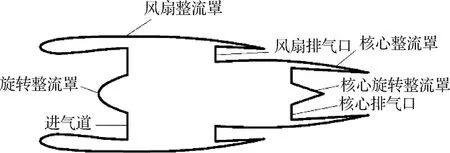
图1 涡扇发动机简化模型[18-19]Fig.1 Simplified model for turbo fan engine[18-19]
1.3 推阻力的定义
对推阻力进行准确定义是计算飞机动力对气动特性影响的重要前提,本节简要介绍采用的推力和阻力分析方法[20]。
流向亚声速飞机动力装置的气流,其流管形状主要由发动机工作状态决定。通过对流过动力装置的内流捕获流管和发动机控制剖面取控制体,可以获得发动机净推力参数。分析发动机的安装推力,还要考虑发动机推力的安装损失,这主要包含流入发动机流管表面上的阻力(即附加阻力)、短舱外表面上的压差阻力、摩擦阻力以及挂架阻力等因素。
如图2所示,对于民用飞机发动机的典型工作状态,从远场(位置0)开始,外部绕过动力装置的气流逐渐减速到进气道唇口的驻点位置(位置i),接着气流从驻点加速直到发动机短舱直径的最大位置(位置M)。和机翼绕流类似,从位置i到位置M 的外罩上作用的气动力合力在轴向的分量成为外罩吸力。由于黏性、分离以及跨声速工作时局部激波的影响,吸力和附加阻力不会全部抵消,其差值称为溢流阻力。在不考虑发动机安装挂架阻力以及干扰阻力的条件下,短舱阻力可以表示为

(2)
式中:p为静压;p0为短舱入口处压力;A为投影面积;τw为短舱壁面摩阻系数。
发动机推力可以表示为
T=∬A[ρu(V·n)+(p-p0)nx-τx·n]dA-
∬A[ρu(V·n)]dA-∬A(-τx·n)dA
(3)
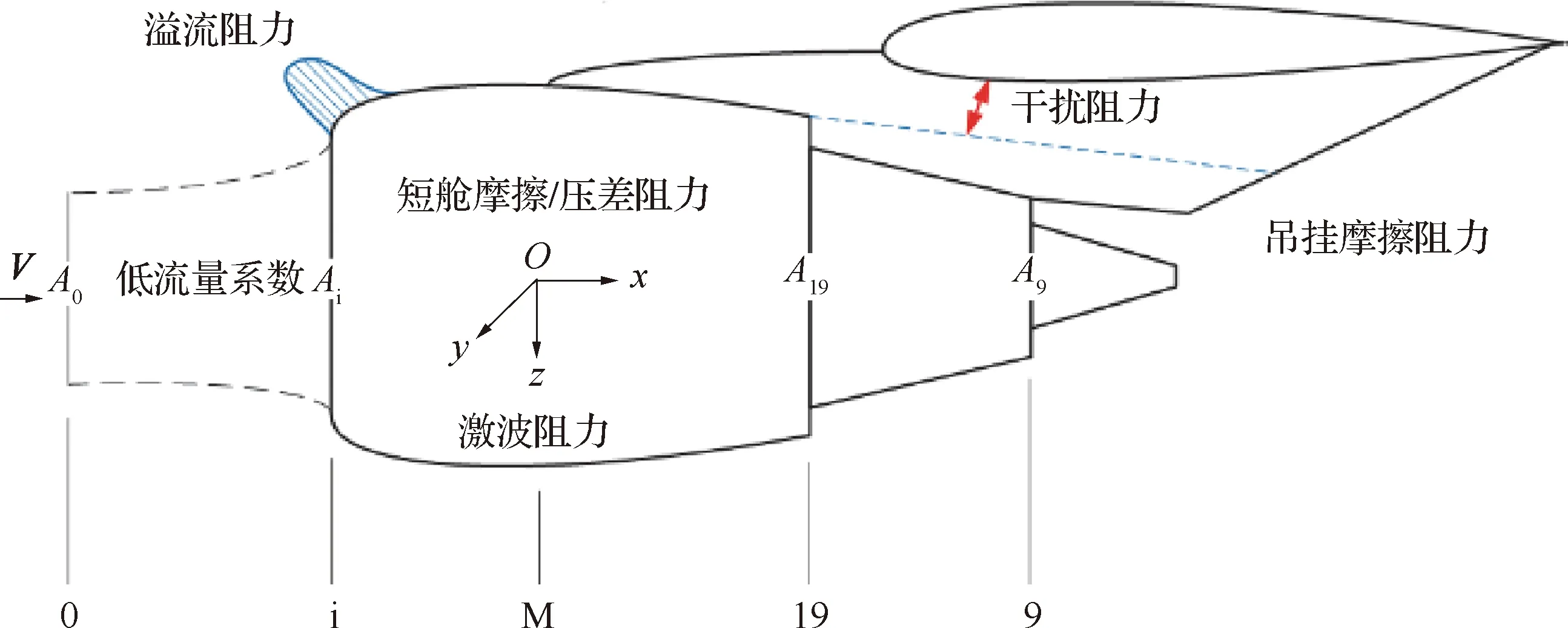
图2 短舱推阻力分析示意图Fig.2 Schematic diagram of analysis of thrust and drag of nacelle
式中:ρ为密度;V为速度;u为速度在流向上的分量;nx为n在流向上的分量;τx为流向上的剪应力。
2 计算方法验证
为了验证本文所采用的动力模型简化方法、网格生成策略以及流场计算方法的正确性,对单独的带动力发动机模型流场进行了数值模拟,并与试验结果进行比较。
本文中采用的单独发动机为一轴对称涡扇发动机模型,取自日本航空宇宙技术研究所“NAL-AERO-02-01” TPS (Turbine Powered Simulation)风洞试验模型[21]。文献[21]给出了该模型的二维半模轮廓线数据,利用建模软件,将该轮廓线绕轴线旋转360°即得到了三维模型,图3为生成的该模型表面网格[21-22]。
发动机的动力效应,通过进排气边界条件确定。本文在风扇进气边界给定质量流量,在内涵和外涵出口边界给定总压、总温和流动方向。
如表1所示,对单独发动机高速巡航状态下的进、排气流场进行了数值模拟和分析(雷诺数Re均为1×106,基于发动机最大直径)。表1中,Ma∞为来流马赫数,α为迎角,MFR为质量流量比,FPR为风扇出口总压比,FTR为风扇出口总温比,CPR为内涵出口总压比,CTR为内涵出口总温比。
图4为两种状态下风扇整流罩和涡轮整流罩表面压力分布计算值与试验值的对比,图中Cp为压力系数,x为沿流向的坐标。两种状态下的计算值与试验值吻合得很好,从而可以验证本文对于单独发动机数值模拟所采用的网格分块策略和进、排气边界处理方法是合适的。
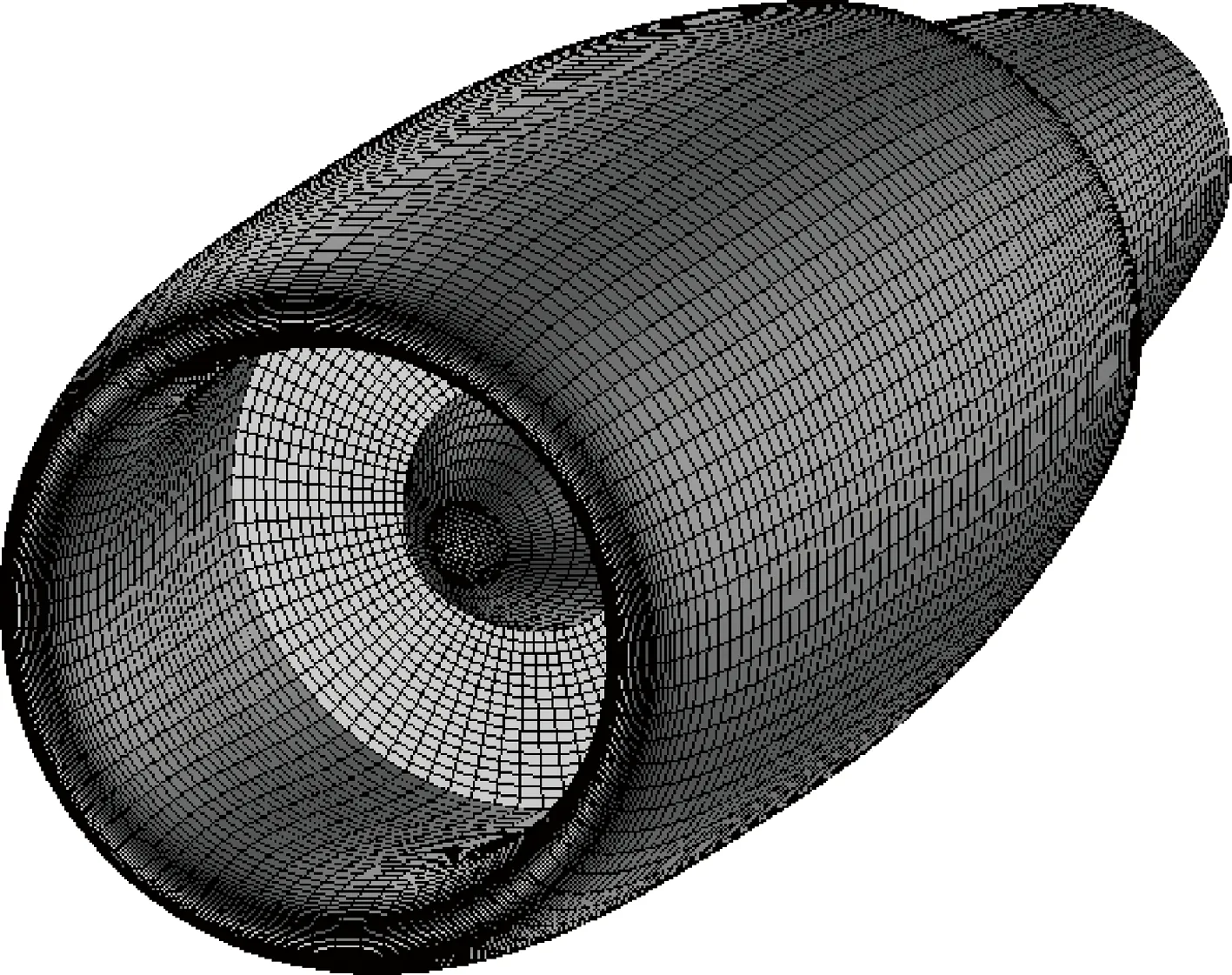
图3 “NAL-AERO-02-01”模型表面网格[21-22]Fig.3 Surface mesh of “NAL-AERO-02-01” model[21-22]
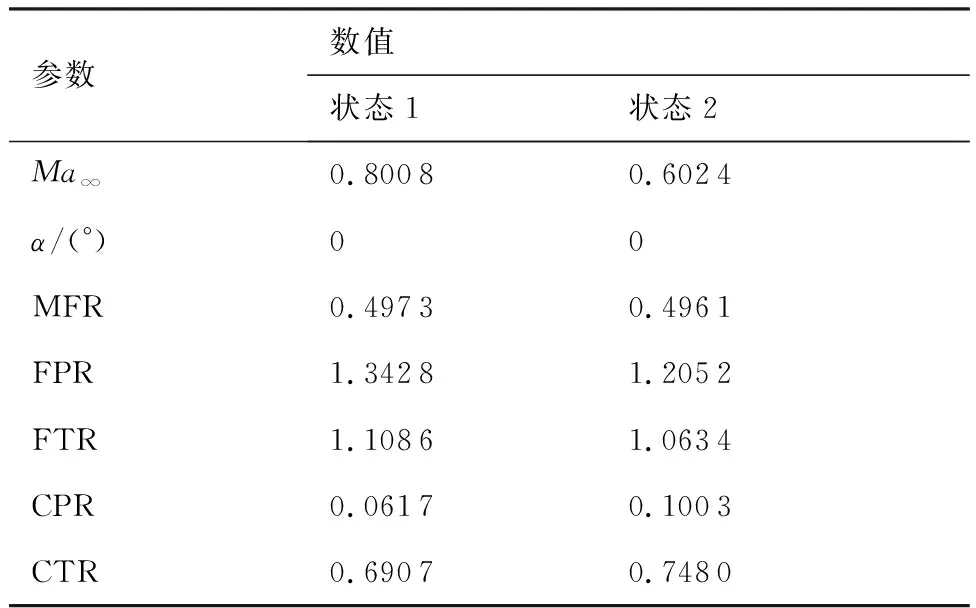
表1 状态参数Table 1 Condition parameters
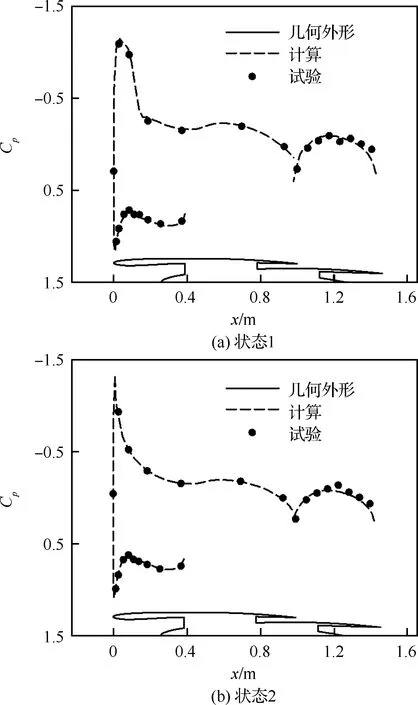
图4 两种状态下表面压力计算值与试验值对比Fig.4 Comparison of surface pressure between computational and experimental results under two conditions
3 BWB全机流场数值模拟
3.1 计算模型和网格
本文针对一种BWB布局的飞机进行了数值计算研究。分别对该飞机的两种不同构型(带动力短舱(Power Nacelle,PN)和带通流短舱(Through Flow Nacelle,TFN))的流场进行计算分析,如图5所示。
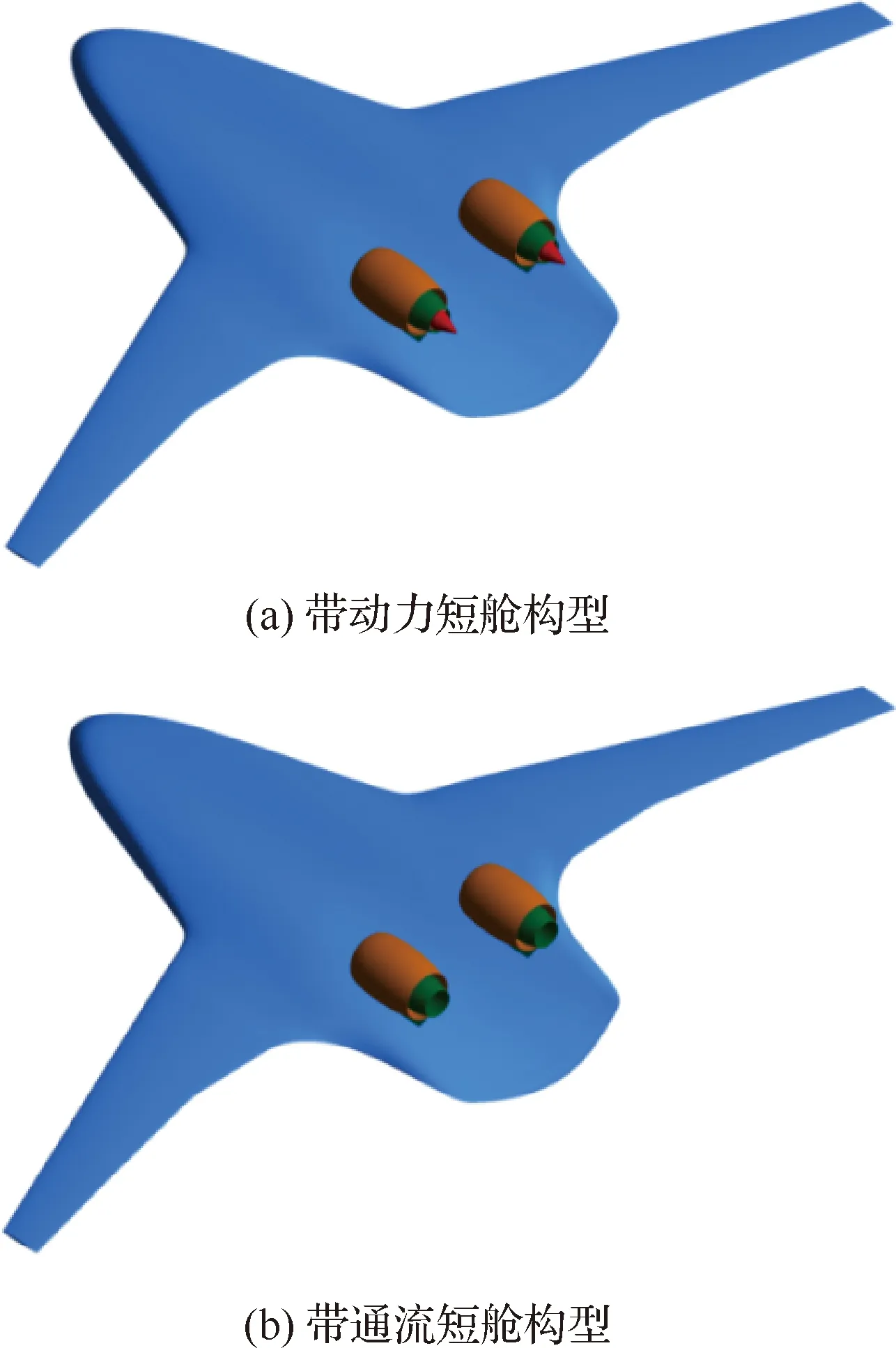
图5 计算采用的两种不同构型Fig.5 Two different configurations for computation
本文中的计算采用多块结构化网格,如图6所示。各块网格可根据各自区域和流场的特点,灵活选择合适的拓扑结构,并安排合理的疏密分布,提高了结构网格处理复杂外形的能力。在近物面区域使用“O”型网格,可以很好地保证近物面网格的正交性,非常适合于模拟飞行器附面层流动。在流场的其他区域使用相对简单的“H”型网格。
文中对飞机-发动机一体化分析,采用统一的模式通过设定进气、排气口边界条件来模拟发动机的动力影响效应。对风扇进气口边界进行简化,通过给定质量流量、压力或者速度等,根据式(4) 可以求得进气口边界的质量流量比MFR,进而求得进气口边界的速度、密度、温度、静压等参数。
(4)
式中:AHL为来流入口边界面积;Afan为风扇入口面积;ρfan为风扇入口处密度;ρ∞为来流密度;qfan为风扇入口处动压;q∞为来流动压。
尾喷口边界分为外涵道喷口和内涵道喷口两部分,内外涵喷口处的马赫数可采用与风扇进气口边界处相同的方法求出。
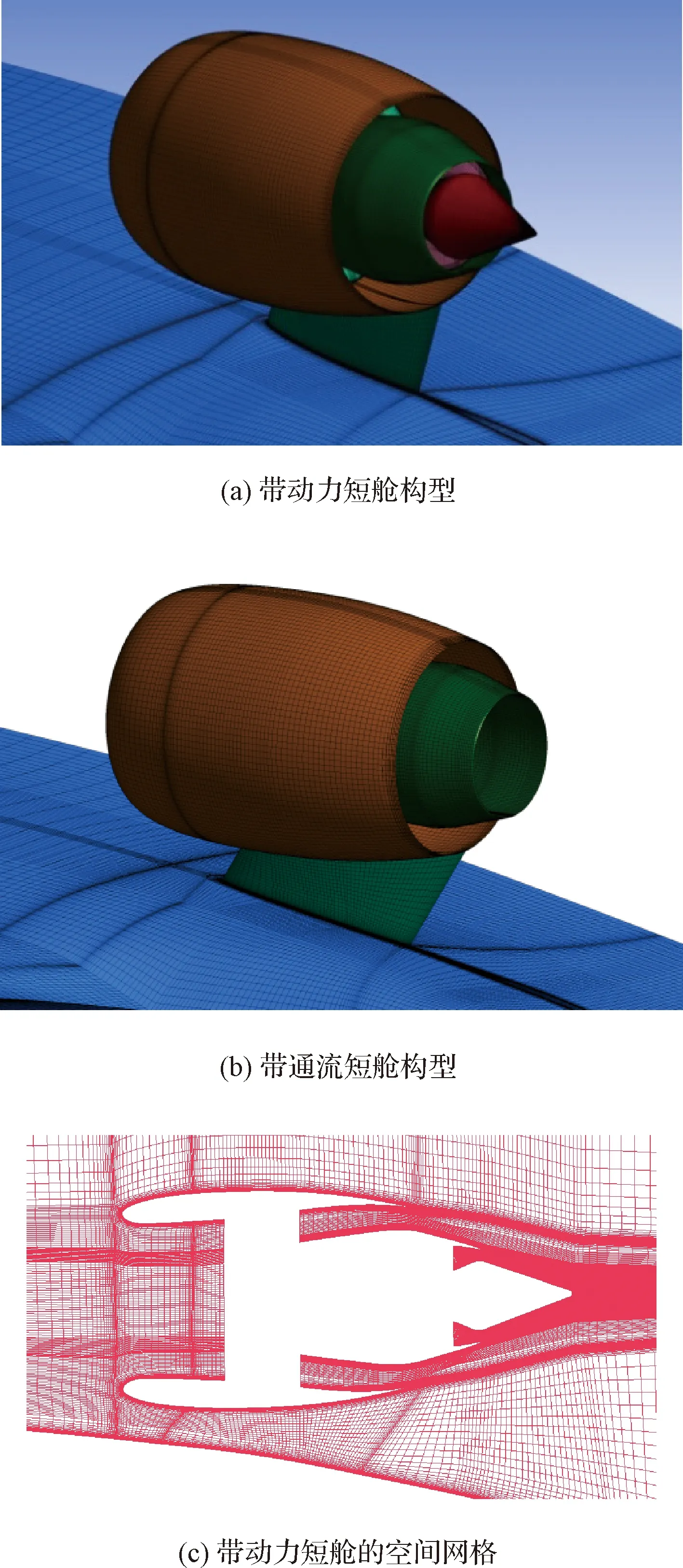
图6 两种不同构型的网格Fig.6 Mesh of two different configurations
3.2 两种构型计算结果
针对上述两种构型在Ma∞=0.8,Re=4.8×107状态的全机气动特性进行计算。图7为两种构型在Ma∞=0.8,α=2°时,表面压力系数的对比。图8为两种构型在Ma∞=0.8时,升阻极曲线的对比(图中CL和CD分别升力系数和阻力系数)。从对比结果看,带动力短舱的全机阻力系数在相同升力系数下比带通流短舱的要大,在巡航迎角(约2°)附近要大约0.002,这主要是由动力短舱和通流短舱在尾喷口的表面压力的差别造成的,这也说明在进行飞机的阻力CFD预测时要对这部分阻力格外注意。
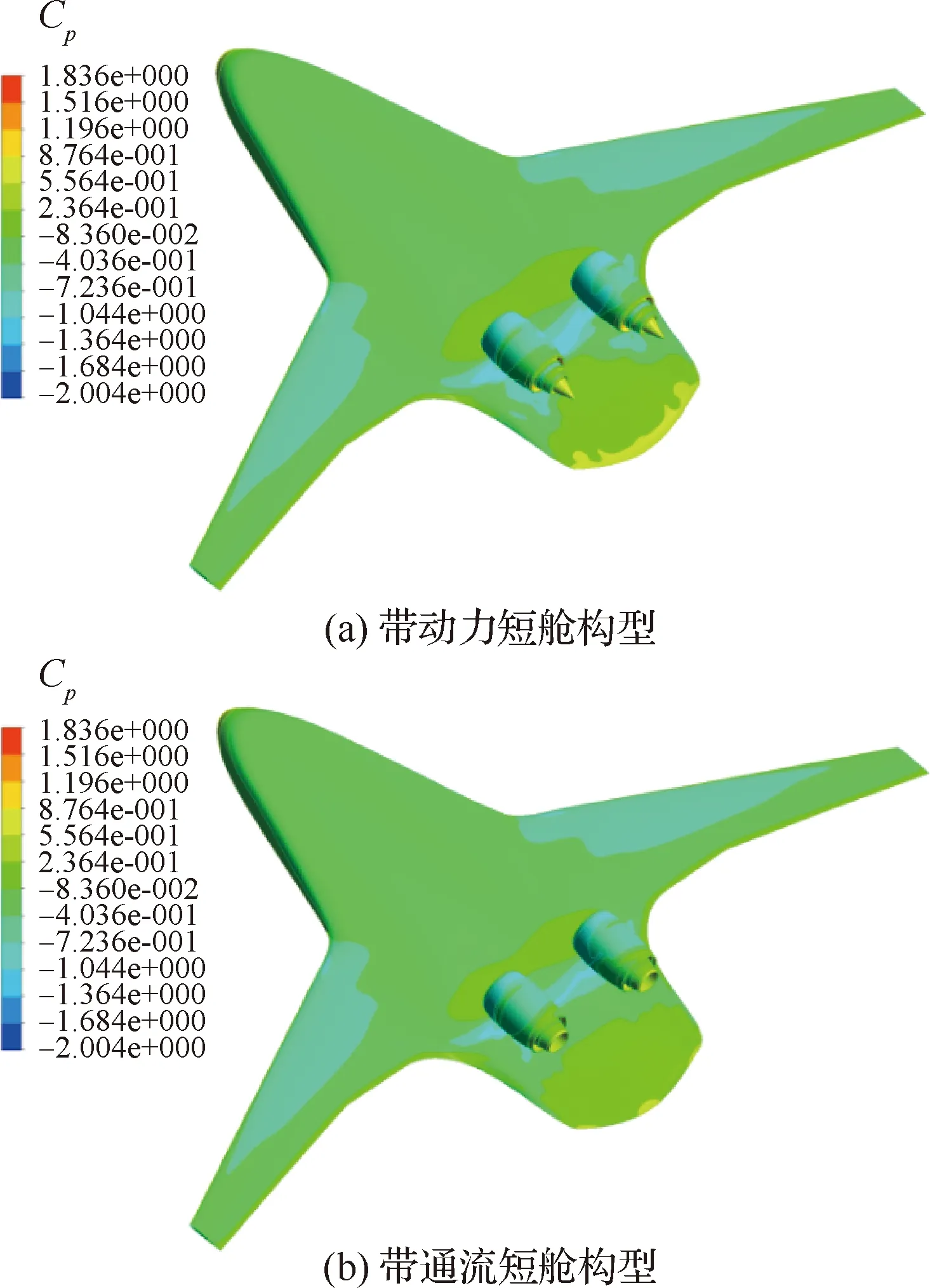
图7 两种构型表面压力系数对比(Ma∞=0.8,α=2°)Fig.7 Comparison of surface pressure coefficient for two configurations (Ma∞=0.8,α=2°)
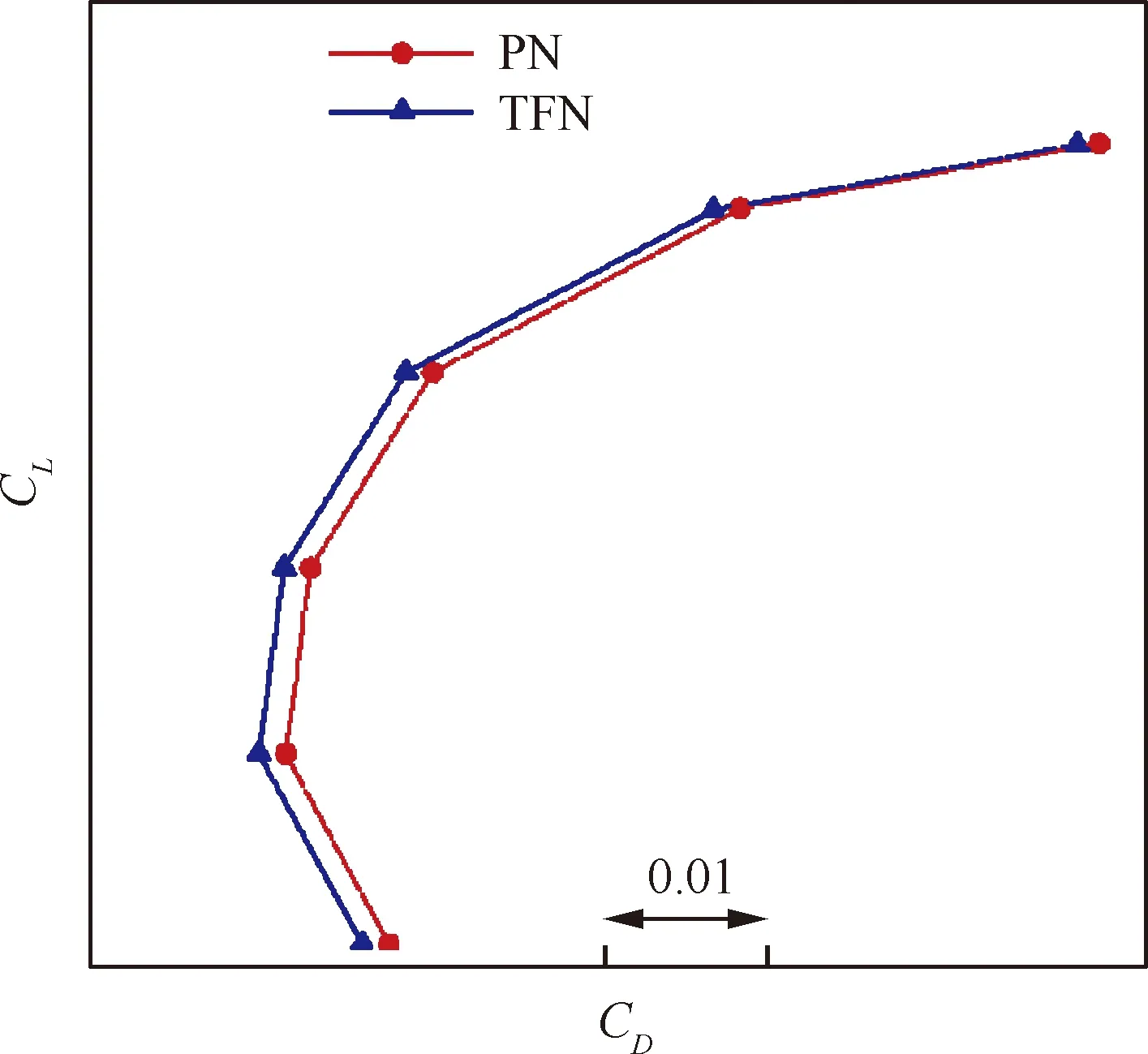
图8 两种构型升阻极曲线对比(Ma∞=0.8)Fig.8 Comparison of lift to drag polar curves for two configurations (Ma∞=0.8)
4 发动机位置参数的影响
本文对发动机短舱不同高度位置、展向位置、流向位置对飞机性能及发动机推力性能的影响进行了研究。此研究是为了发现相关规律性的问题,因此并没有考虑飞机的结构、布置等的可实现性,有些位置变化会非常大。同时,为了单纯研究发动机位置变化的影响,将发动机挂架去掉,并采用通流短舱构型。本节针对Ma∞=0.8,Re=4.8×107,α=2°状态下的全机气动性能及发动机推力性能进行计算。
4.1 短舱高度位置对飞机性能的影响
不同发动机高度位置示意如图9所示。选择了发动机轴线距离机身上表面由低到高的8个发动机位置进行研究,升力系数及升阻比随发动机高度(h)增加而变化的曲线如图10所示。从图中可以看出,随着发动机高度的增加,升力系数显著上升,升阻比上升。
为了分析发动机高度变化导致升阻力变化的原因,做出发动机中间截面压力分布,如图11所示。从图中可以看出,短舱位置较低时,短舱下部和机身上表面会产生相互干扰,出现一个较大的低压区,对阻力产生影响。随着短舱位置的升高,低压区范围减小。
图12是发动机推力随短舱高度的变化,图中横线是CFD计算得到的单独发动机的推力值。发动机推力随着离机身高度的增加是先增大再减小。高度较小(0.5 m以内)时,由于受气流分离的影响,推力相对单独发动机推力值减小,而随着分离的消失,机身反而会产生有利的干扰,使发动机的推力增大,但高度到一定程度后,有利干扰越来越小,推力就又慢慢减小。这个现象与常规布局民机的现象不太一样。这一研究也为后续BWB布局飞发一体化设计提供了一些参考。
图9 不同短舱高度位置Fig.9 Different height locations of nacelle
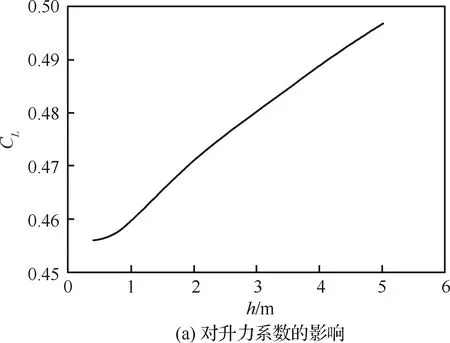
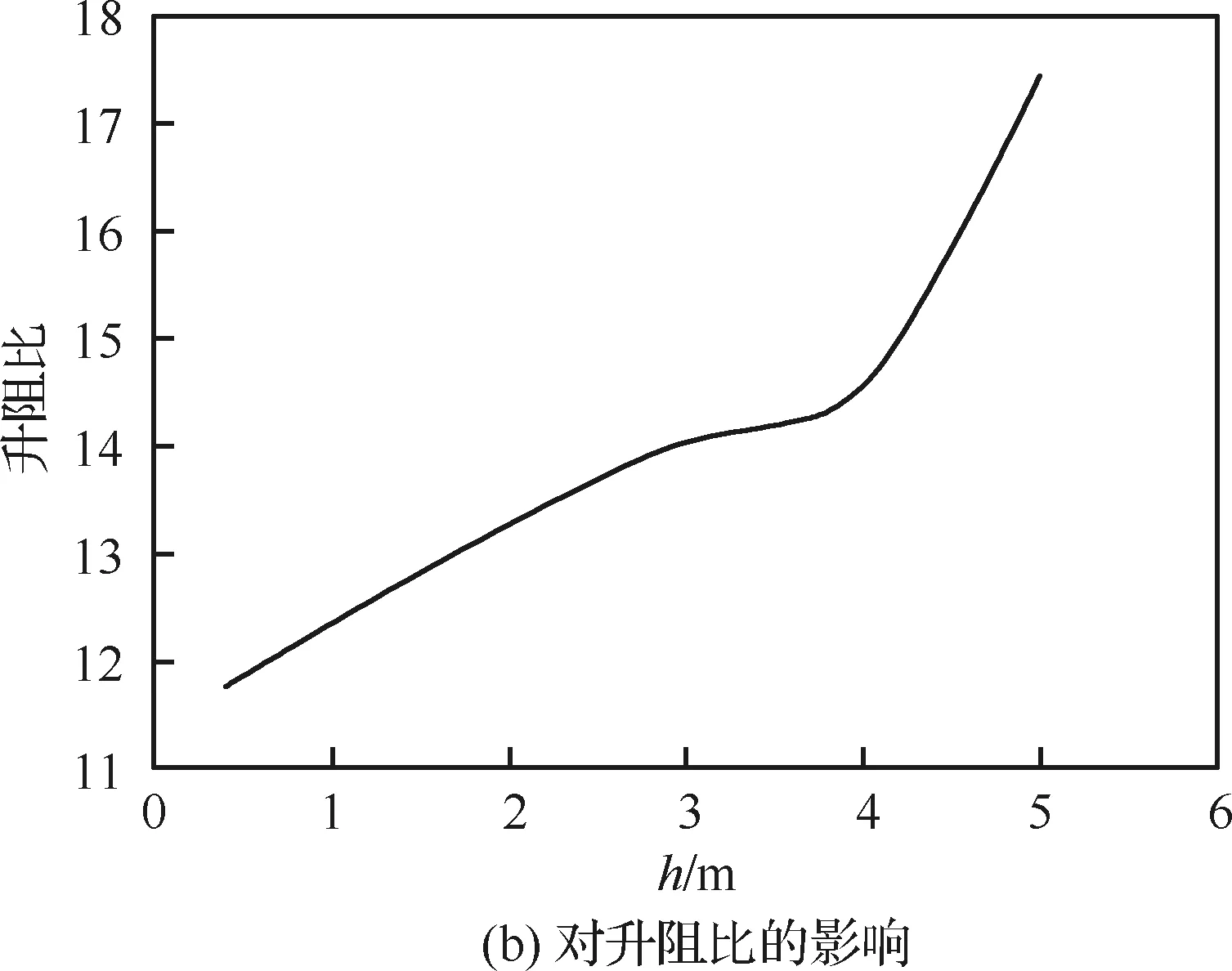
图10 不同短舱高度对升力系数、升阻比的影响Fig.10 Influence of different nacelle heights on lift coefficient and lift-to-drag ratio

图11 不同高度短舱中间截面压力分布Fig.11 Distribution of pressure on middle slice for different height nacelles
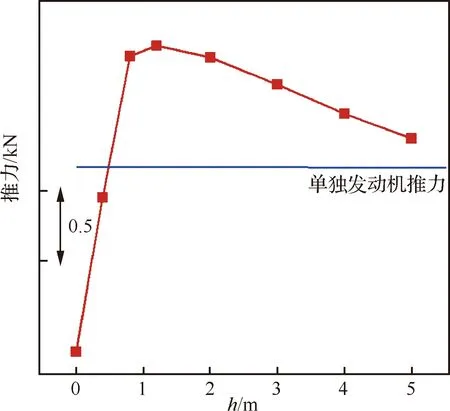
图12 推力随短舱高度的变化Fig.12 Variation of thrust with nacelle height
4.2 短舱展向位置对飞机性能的影响
选择发动机轴线距离飞机对称面由内向外3个位置进行研究,如图13所示。
升力系数及升阻比随发动机展向位置变化的曲线如图14所示。由图可知,发动机展向位置越靠内,升力越大,升阻比越小;越靠外,升力越小,升阻比越大。
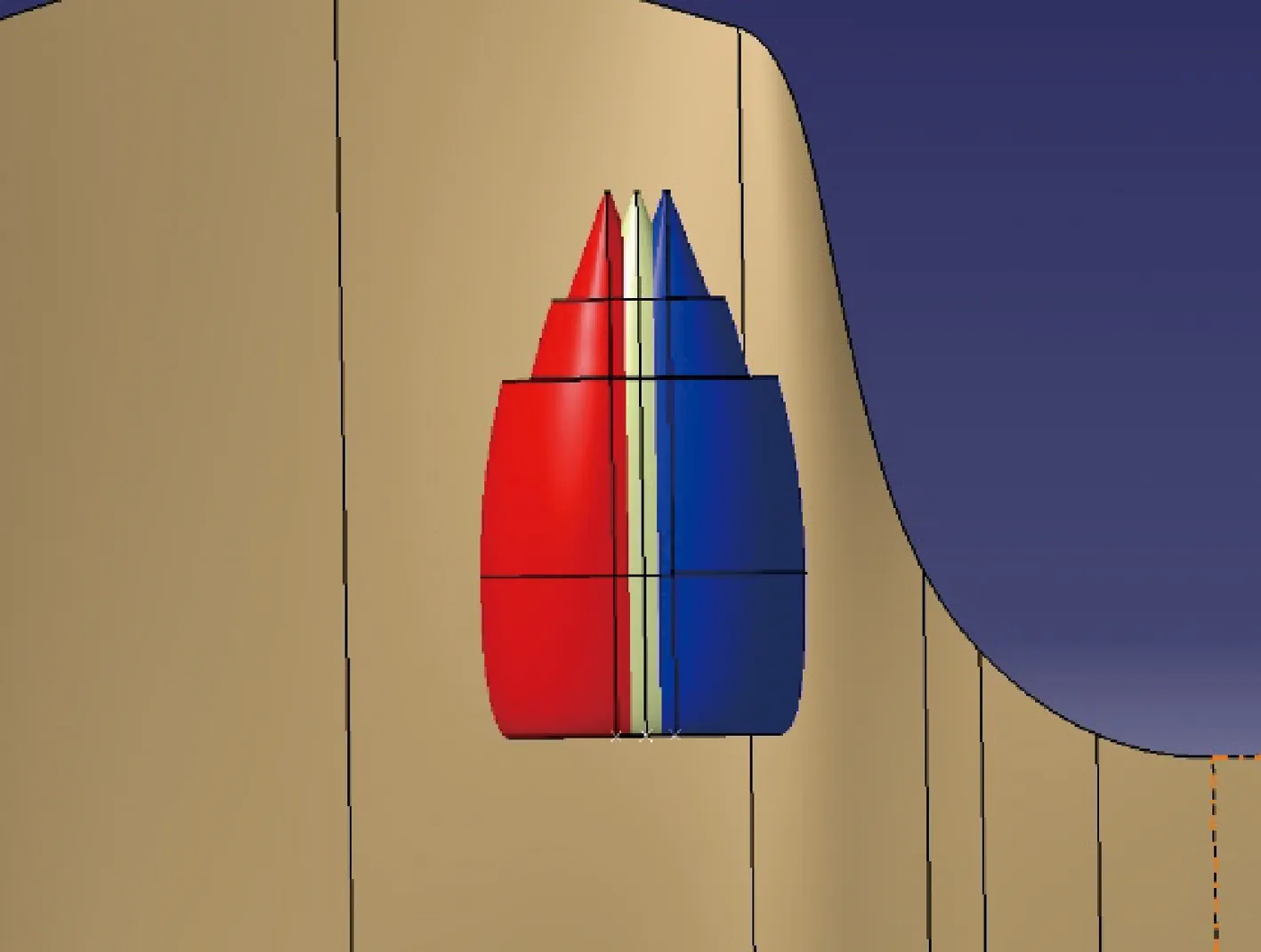
图13 不同短舱展向位置Fig.13 Different spanwise locations of nacelle
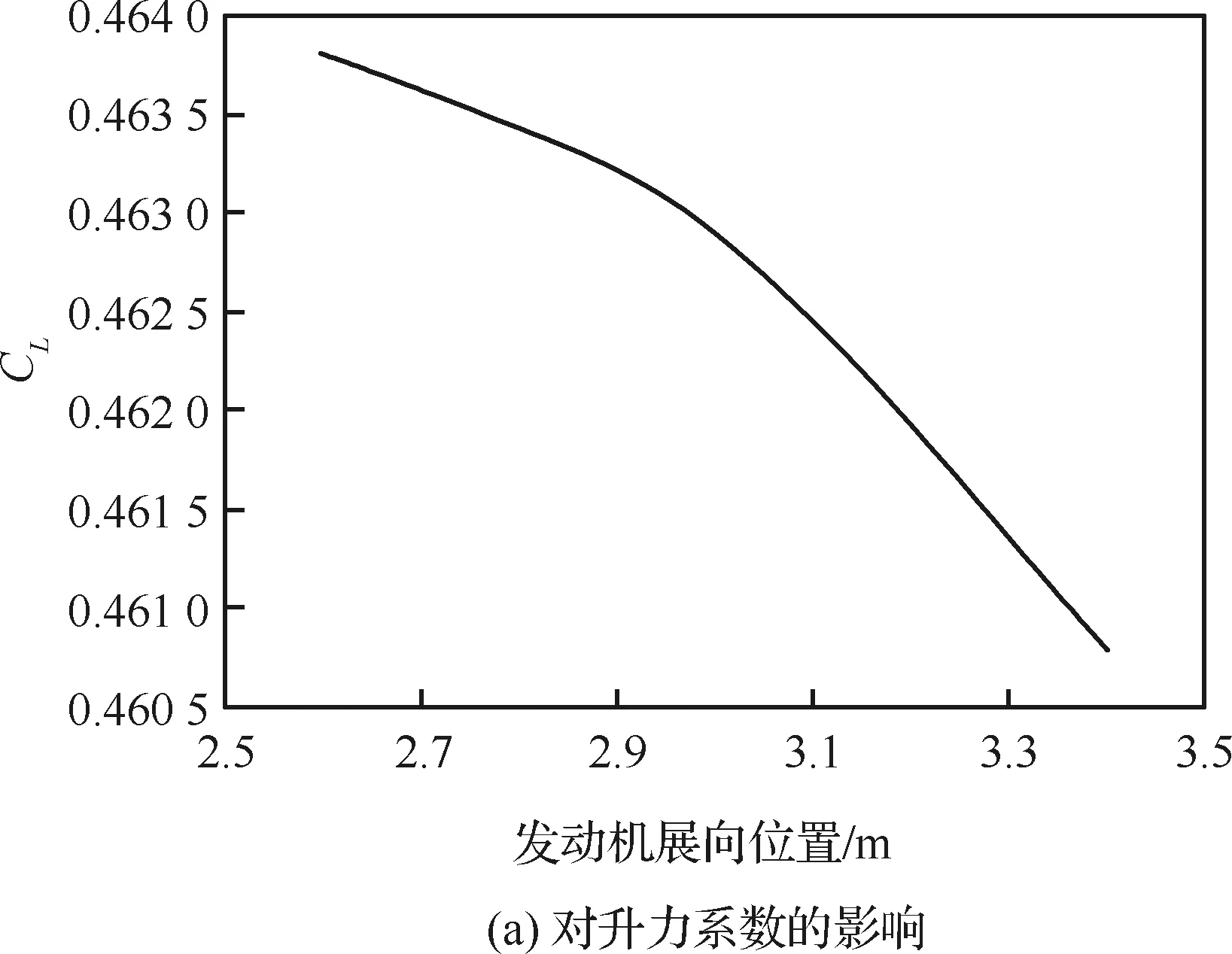
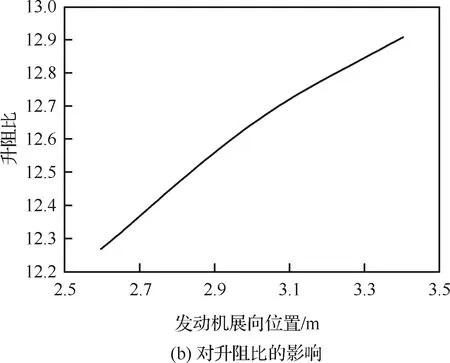
图14 不同短舱展向位置对升力系数、升阻比的影响Fig.14 Influence of different nacelle spanwise locations on lift coefficient and lift-to-drag ratio
4.3 短舱流向位置对飞机性能的影响
选择发动机入口截面距离机头由前到后3个位置进行研究,升力系数及升阻比随发动机展向位置变化的曲线如图15所示。由图可知,发动机展向位置越靠后,升力越大,升阻比也越大;越靠前,升力越小,升阻比也越小。
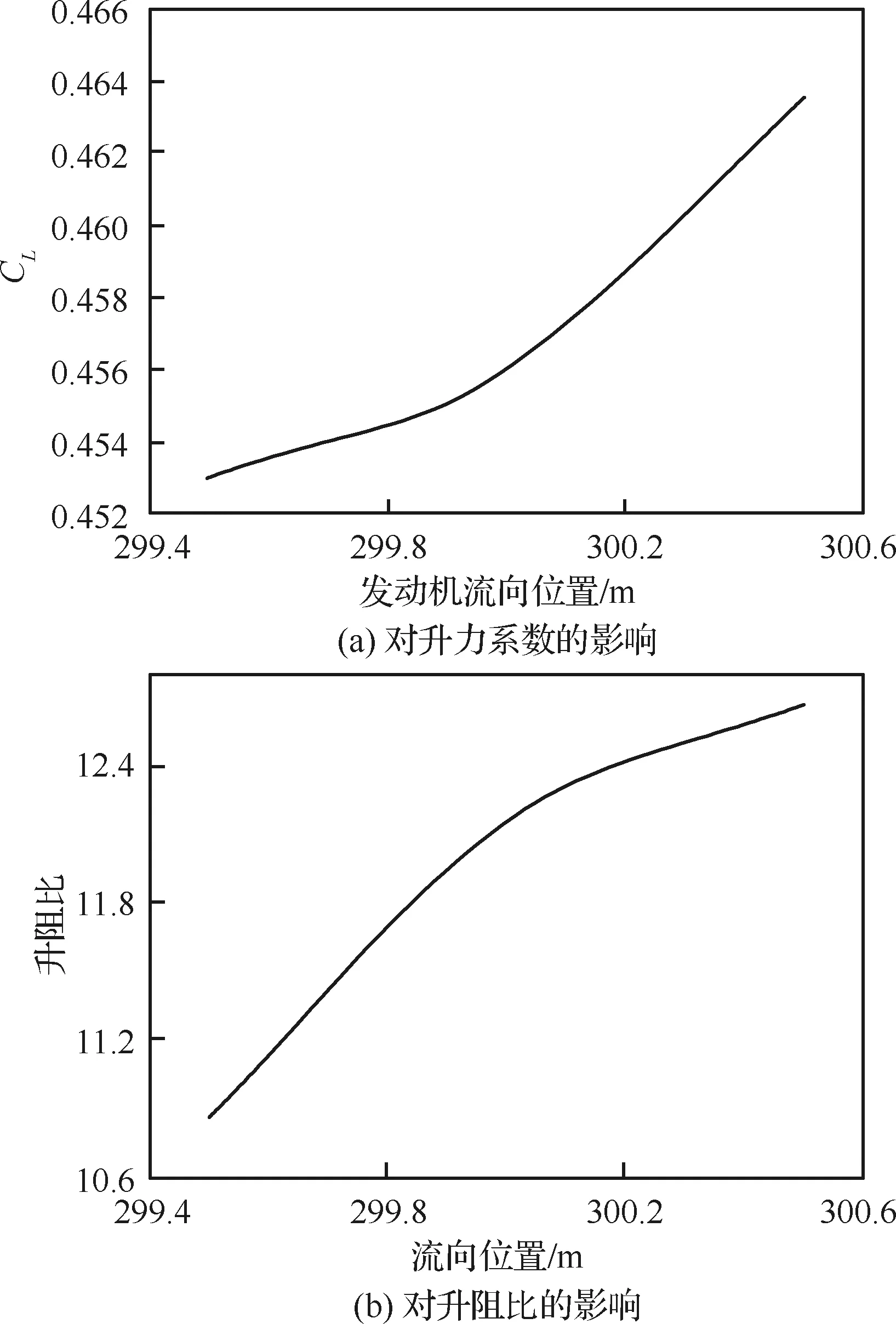
图15 不同短舱流向位置对升力系数、升阻比的影响Fig.15 Influence of different nacelle streamwise locations on lift coefficient and lift-to-drag ratio
5 结 论
1) 所采用发动机简化模型和推阻力定义方法能够准确地模拟发动机的动力效应。
2) 带动力短舱后全机的阻力较通流短舱会有明显增加。
3) 随着发动机离机身高度增大,发动机推力先增大后减小,飞机升力增大,升阻比增大。
4) 随着发动机展向位置向外移动,飞机升力减小,升阻比增大。
5) 随着发动机流向位置向后移动,飞机升力增大,升阻比增大。
致 谢
感谢西北工业大学张彬乾教授课题组的支持与帮助,感谢上海飞机设计研究院同事们的指导与建议。
