考虑测试性设计缺陷修正延时的测试性增长模型建模与评价方法

李天梅，司小胜，杨宗浩，徐从启，张琪

1.火箭军工程大学 导弹工程学院，西安 710025 2.火箭军士官学校，青州 262500 3.中国人民解放军32181部队，西安 710032

测试性增长模型(Testability Growth Model，TGM)是跟踪并预计装备测试性水平增长过程的数学模型，是装备测试性增长分析过程的核心要素。而为了更加方便有效地实现测试性增长跟踪与预计，需要建立测试性增长参数化学习曲线时间函数模型[1-2]。

近年来，测试性增长建模相关问题已成为测试性工程领域的热难点问题。Li等[3]研究建立了测试性增长参数化学习曲线时间函数模型，该模型通过分析测试性设计缺陷(Testability Design Limitation，TDL)变化规律，构建具有铃形变化规律的测试性增长效能函数来表征已识别TDL数量变化趋势，并假设TDL在识别后立即被修正，不存在时间延迟，且不引入新的TDL。Zhao等[4-5]针对试验过程中故障模式可能发生变化的情况，并假设对识别的TDL不能一次性根除，分析测试性指标变化规律，提出了一种基于马尔科夫链考虑非理想修正的测试性增长参数模型。该模型是以单个故障模式不可检测/隔离概率作为马尔科夫链的状态转移概率，但对于大型复杂装备，每个故障模式的不可检测/隔离概率数据很难获取，且所获取数据具有很大的不确定性，因此影响所建立测试性增长参数模型的准确性。

以上模型的提出对测试性增长试验的开展具有重要理论指导意义，但这些模型忽略了测试性设计者的学习过程和TDL修正延时问题。测试性设计者学习过程是指随着装备测试性增长过程的进行，测试性设计人员对系统越来越了解，对测试性设计技术越来越熟悉，对TDL修正能力越来越强。修正延时是指TDL修正过程滞后于TDL识别过程的现象，从时间角度来看就是TDL被识别之后到完全被修正所需要的那一段时间。因此，如何考虑测试性设计者的学习过程和修正延时现象建立准确的测试性增长参数化学习曲线时间函数模型十分必要。

在软件可靠性领域中，有大量考虑故障修正延时的软件可靠性增长模型。Schneidewind[6]首先提出故障修正过程是影响可靠性和测试进度的主要过程，他从时间角度分析了故障修正延迟现象，并在假设修正延迟是一个常数的基础上建立了故障修正过程的软件可靠性增长模型。在此基础上，一些学者还提出了基于不同时间延时函数的软件可靠性增长模型[7-9]。在测试性增长过程中，修正TDL是测试性设计增长的主要目的，对于不同的TDL其修正的难易程度不同，需要的修正时间不同，同时，随着测试性设计者学习过程的存在，很难用一种时间延时函数统一描述。然而与描述每个TDL的延时时间相比，测定已识别TDL数量和已修正TDL数量是较为简单的和可行的。事实上，测试性增长的目的就是逐一识别并修正TDL，这里将已经识别到但未修正的测试性设计缺陷，称为剩余测试性设计缺陷(Remaining Testability Design Limitation，RTDL)，RTDL数量能直接反映测试性设计水平的高低。

基于以上分析，本文考虑测试性设计者的学习过程，在分析TDL识别过程与修正过程存在延时关系的基础上，通过分析TDL识别与修正机理及变化规律，构建具有铃形变化规律的剩余测试性设计缺陷函数，在此基础上，研究建立基于Gamma、Rayleigh和Delay-S 3种铃型曲线考虑修正延时的测试性增长参数化学习曲线时间函数模型；最后，基于某机载稳定跟踪平台的增长试验数据，验证所提测试性增长模型的有效性。

1 RTDL变化趋势分析

在实际的测试性增长试验中，TDL必须在被识别之后才能被修正。一般来说识别的测试性缺陷数量越多，修正的TDL也随之增多。与此同时，修正的TDL数量越多，TDL修正人员积累的经验也越多，可以更容易对已识别的TDL进行修正。

在测试性增长试验初期，随着注入的故障模式数量逐渐增加，TDL逐渐被识别，已识别TDL数量不断增多。此时，由于设计师缺乏经验，TDL不容易被修正，所用的修正时间较长，TDL修正效率较低，TDL的修正过程将滞后于TDL的识别过程，RTDL不断增大。随着测试性增长试验的进行，在规定的故障注入次数下，能识别的测试性设计缺陷数量逐渐达到饱和，设计师不断学习，对仪器、工具、方法逐渐掌握，经验不断积累，TDL的修正效率不断提高，RTDL数量逐渐减小，TDL的修正过程逐渐逼近TDL的识别过程。而且RTDL能够从测试性设计缺陷数量上直接反应修正延时的变化过程，且具有“先增后减”的变化趋势。

衡量测试性的指标包括故障检测率(Fault Defection Rate，FDR)、故障隔离率、以及虚警率等，这些指标在数学上没有相关性。因此一般情况下，一次测试性增长试验只能以一个测试性指标增长为目标。不失讨论问题的一般性，接下来的论文部分以FDR增长模型建模为例展开讨论。

2 考虑TDL修正延时的FDR增长模型

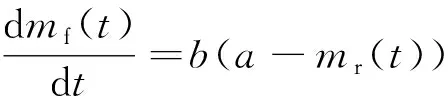
(1)

式中：a为最初隐藏于系统中的TDL数量；b为比例系数，不失讨论问题的一般性，假设b为常数；mf(t)为识别出的TDL数量；mr(t)为识别并有效修正的TDL数量。

由第1节分析可知，由于存在测试性设计者的学习过程，导致TDL在识别出来后不能被立即修正，即存在TDL的修正延时问题。RTDL数量记为y(t)，即

mf(t)-mr(t)=y(t)

(2)

将式(2)代入式(1)可得

(3)

FDR的数学模型可表示为

(4)

式中：M为故障模式总数，可以通过故障模式影响及危害性分析得到；ND为系统测试性设计能够成功检测到的故障模式数量。

ND的表达式为

ND=M-(a-mr(t))

(5)

ND=M-[a-(mf(t)-y(t))]

(6)

将(6)式代入(4)式可得

(7)

式中：q(t)即为考虑TDL修正延时的测试性增长参数化学习曲线时间函数模型的一般表达形式。

由于测试性试验工程师具有一定的学习能力，随着测试性增长试验的开展，RTDL数量具有先增后减的变化趋势，借鉴软件可靠性增长领域考虑学习过程的铃形曲线形式[10-13]，分别采用Gamma、Rayleigh和Delay-S 3种铃形曲线表示RTDL变化趋势，将这3种曲线代入式(6)，即可得到考虑TDL修正延时的3种不同曲线特性下的FDR增长模型。

2.1 基于Gamma修正延时曲线的FDR增长模型

Gamma曲线可以表示为[10]

(8)

由式(8)可知，Gamma曲线是一条光滑的铃形曲线，如图1所示。

图1 具有固定参数的Gamma函数曲线(α=240, β=1.496, θ=5.96)Fig.1 A Gamma curve with fixed parameters (α=240, β=1.496, θ=5.96)

将式(8)代入式(3)可得

(9)

在边界条件mf(0)=0下求解微分方程式(9) 可得

(10)

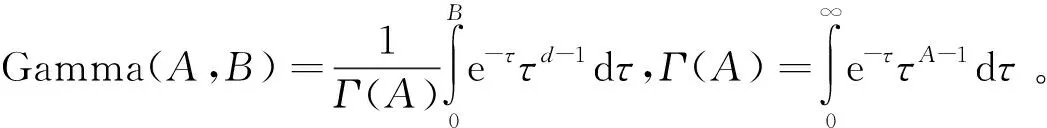
将式(10)代入式(7)，可得基于Gamma修正延时曲线的FDR增长参数化学习曲线时间函数模型为

(11)

2.2 基于Rayleigh修正延时曲线的FDR增长模型

Rayleigh曲线可以表示为[11]

(12)

由式(12)可知，Rayleigh函数是一条光滑的铃形曲线，如图2所示。

将式(12)代入式(3)可得

(13)

在边界条件mf(0)=0下求解微分方程(13)可得

(14)

将式(14)代入式(6),可得基于Rayleigh修正延时曲线的FDR增长参数化学习曲线时间函数模型为

(15)

图2 具有固定参数的Rayleigh函数曲线(α=240, β=0.111 1)Fig.2 A Rayleigh curve with fixed parameters (α=240, β=0.111 1)

2.3 基于Delay-S修正延时曲线的FDR增长模型

Delay-S曲线可以表示为[12-13]

y(t)=αβ2te-β t

(16)

由式(16)可知，Delay-S函数是一条光滑的铃形曲线，如图3所示。

将式(16)代入式(3)可得

(17)

图3 Delay-S函数曲线示意图 (α=240, β=0.111 1)Fig.3 A Delayed-S curve with fixed parameters (α=240, β=0.111 1)

在边界条件mf(0)=0下求解微分方程(17)可得

(18)

将式(18)代入式(6)，可得基于Delay-S修正延时曲线的FDR增长参数化学习曲线时间函数模型为

q(t)=1-

(19)

3 试验验证

3.1 试验数据说明

为验证本文所建TGM的有效性，以某型机载稳定跟踪平台控制系统为对象开展了测试性增长试验，具体的试验数据见表1。对该机载稳定跟踪平台开展故障模式影响及其危害性分析得到该平台有350个功能故障。在研制阶段共投入24周时间开展测试性增长试验，在这24周时间里，通过注入313个板级功能故障，识别了86个TDL。测试性设计者分析导致TDL的根本原因并改进测试性设计，共修正了80个TDL。

基于表1所列数据，已识别TDL数量、已修正TDL数量和RTDL数量变化趋势如图4所示。

从图4中可以看出已识别的TDL数量和已修正的TDL数量变化趋势十分相似，表明两者之间存在一定的相关性。而RTDL数量并不是常数，在测试性增长试验的开始阶段，RTDL数量不断增长，而在增长试验的后期，RTDL数量不断减小，具有先增后减的铃形变化趋势。

表1 某机载稳定跟踪平台测试性增长试验数据Table 1 Test data of a stable tracking platform

图4 已识别TDL、已修正TDL和RTDL数量变化趋势Fig.4 Variation tendency of identified TDL, corrected TDL and RTDL

3.2 TGM参数估计

本文采用最小二乘方法估计得到式(10)、式(14)、式(18)中的参数。

以式(18)中参数估计为例，首先计算

(20)

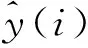
式(20)分别对参数集合η1={α,β}求偏导数可得

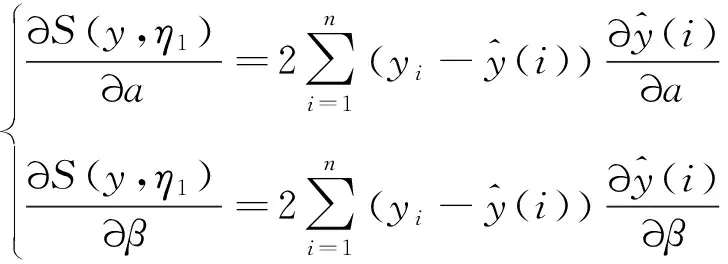
(21)

代入具体的表达式和数据，通过最小二乘求极值原理可得到参数估计结果为：α=674.46、β=0.084 8。

将求得的α=674.46、β=0.08代入式(18)后，计算可得

(22)

式(22)分别对参数集合η2={a,b}求偏导数可得

(23)

代入具体的表达式和数据，通过最小二乘求极值原理可得到参数估计结果为：a=46.03、b=0.18。

同理，可以计算得到式(10)、式(14)中具体参数估计结果，见表2。

基于表2的参数估计结果，图5给出了实际剩余测试性设计缺陷数量变化曲线和基于Gamma、Rayleigh和Delay-S 3种铃形曲线拟合出来的剩余测试性设计缺陷数量变化趋势图。

图6给出了实际检测到测试性设计缺陷数量变化曲线和基于式(10)、式(14)、式(18)计算得到的已检测出测试性设计数量变化趋势图。

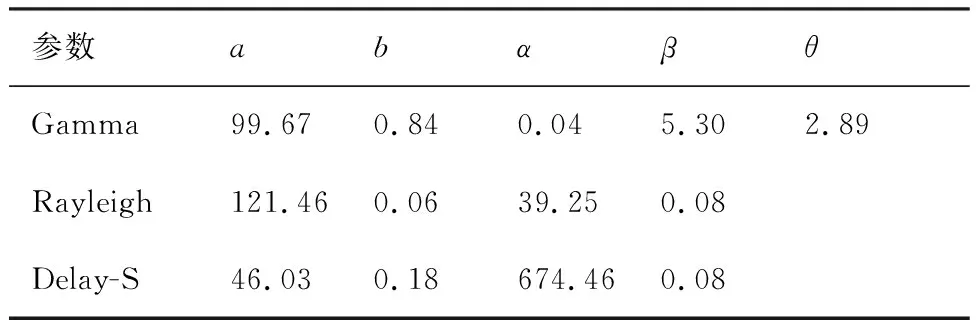
表2 最小二乘参数估计值Table 2 Estimation values based on LSE

图5 实际的和铃形曲线拟合的RTDL数量Fig.5 Actual number of RTDL and fitting number of RTDL

图6 实际的和拟合的已识别测试性设计缺陷个数Fig.6 Actual number and fitting number of identified TDL

3.3 TGM评估指标

下面分别从拟合能力、估计精度和预测能力3个方面给出TGM的评价指标。

1) 误差平方和(Sum of Square due to Error，SSE)

SSE反映了估计值和实际值之间的偏差,SSE的定义为[14-15]

(24)

式中：n为测试性增长试验阶段数；yi为经过实际测试性增长试验后累计的RTDL数量；y(i)为测试性增长跟踪与预计计算得到的RTDL数量。SSE越小，说明模型拟合效果越好。

2) 估计精度(Accuracy of Estimation，AE)

AE的定义为[14-15]

(25)

式中：mr为通过测试性增长试验累计修正的TDL数量；a为估计得到的装备系统最初包含TDL数量。AE越小，说明模型估计精度越高。

3) 相对误差(Relative Error，RE)

RE定义为[14-15]

(26)

3.4 TGM效果分析

本文建立的考虑TDL修正延时的TGM，其SSE和AE计算结果见表3。

分析表3中数据可得，基于Gamma铃形修正延时曲线建立的测试性增长模型，其SSE和AE值相对较小，表明该模型具有很好地拟合和估计能力。图5和图6的示意图中也说明了这一结论。

图7描述了基于3种铃形修正延时曲线建立的测试性增长模型在RE这一指标的变化趋势。由图7可以看出，基于Gamma铃形修正延时曲线建立的测试性增长模型计算得到的RE值相对于其他两种模型要小，且跟踪与预计精度能达到10-2数量级。

表3 3种模型指标估计值Table 3 Estimate values of SSE and AE

图7 基于3种铃形曲线的RE变化趋势Fig.7 Variation tendency of RE based on three bell shaped curves

将表2计算得到的参数估计值代入式(11)绘制基于Gamma修正延时曲线的FDR增长试验跟踪与预计曲线，同时基于表1的测试性增长试验数据绘制该机载稳定跟踪平台实际FDR增长曲线，如图8所示。

图8 基于Gamma曲线的FDR增长曲线Fig.8 Variation tendency of FDR based on Gamma curves

4 结 论

1) 分析了剩余测试性设计缺陷具有先增后减的铃形变化趋势，提出基于Gamma、Rayleigh和Delay-S 3种曲线来拟合剩余测试性设计缺陷变化趋势，数据应用表明Gamma曲线拟合精度更高。

2) 以故障检测率为具体的增长指标，研究建立了基于3种剩余测试性设计变化趋势曲线(Gamma, Rayleigh和Delay-S)、考虑修正延时的FDR增长模型，从拟合精度、估计精度和预测精度上给出了3个评价指标。试验数据应用表明基于Gamma曲线考虑修正延时的测试性增长模型可以较精确地描述装备测试性指标在测试性增长过程中的变化规律，跟踪与预计精度能达到10-2数量级。