三种用于加工特征识别的神经网络方法综述

2019-09-25石叶楠郑国磊

航空学报 2019年9期

石叶楠，郑国磊

北京航空航天大学机械工程及自动化学院，北京 100083

加工特征自动识别是智能化设计与制造领域中的一项核心技术和关键支撑，在所有借助特征进行分析与决策的计算机辅助设计与制造系统中，特征识别均是必不可少的基础组成单元。在当下的数字化设计与制造中，设计完成的计算机辅助设计(Computer Aided Design, CAD)模型用于计算机辅助制造(Computer Aided Manufacturing, CAM)时，常常存在数据与物理环境间脱节的问题，即物理制造阶段仅传递面、边等低级信息，而丢失CAD模型设计中的其他相关信息。计算机辅助工艺规划(Computer Aided Process Planning, CAPP)从制造需求的角度对CAD模型进行解释，并重新用“加工特征”来定义，从而解决了CAD和CAM之间的连接问题。

加工特征与加工过程密切相关，涉及加工方式、刀具类型、加工刀轨、夹具等信息。根据加工特征的几何性质和在CAD模型中的空间关系，通常将其分为独立特征与相交/复合特征。相交特征由多个独立的特征组合形成，并在几何或拓扑结构上发生了改变，其识别是加工特征识别中的难点和重点。现有的加工特征识别方法已得到了广泛的应用，但是特征识别方法仍然面临三方面的挑战：一是特征本身具有多样性，而不同的应用系统仅根据需要寻求预定特征的识别算法，使得算法不具通用性，无法适应特征多样性的发展要求；二是特征识别的时间成本较高，特别是在处理复杂特征、相交特征或大型结构件中的多类型特征时，识别时间可能会大幅增加；三是准确率还需进一步提高。

目前针对加工特征识别的方法有很多，其中比较经典的方法可归纳为基于图的方法[1]、基于体分解的方法[2]、基于规则的方法[3]和基于痕迹的方法[4]。这些方法各有优缺点，但是它们间的共性问题包括：① 不具备学习和抽象能力；② 对CAD输入模型的抗噪性较差；③ 专注于特定类型的CAD表示，不能推广到其他不同表示方法的特征表示；④ 处理可变特征、相交特征的能力较差。

恰恰相反，神经网络方法具有弥补这些共性不足的技术优势。首先，神经网络具有学习的能力；其次，神经网络方法是基于数据驱动的方法，只要建立了一种通用的数学表达方法，就可以统一用神经网络识别不同类型的特征；再次，神经网络具有识别相似特征的能力，不需要预定义所有可能的特征实例。因此，自20世纪90年代末开始，国内外学者开始关注和研究利用神经网络识别加工特征，并取得了一系列显著的成果[5-6]。神经网络方法的基本思想是借助神经网络的学习能力，通过向网络输入样本特征并依据期望输出结果来反复训练网络，以实现特征识别任务。同时，神经网络的抗噪性能也有助于提高特征识别的准确率。目前，这方面的研究重点在于：① 如何将CAD模型和加工特征转化为神经网络的输入信息，即特征的预处理和编码；② 选择何种神经网络，即神经网络构架。

神经网络在计算机视觉与模式识别中的巨大成功已验证了其强大的识别与分类能力，类比可见神经网络方法在加工特征识别领域也很有发展潜力。本文针对目前神经网络在识别加工特征方面的能力和所取得的成果，综述多层感知机(Multilayer Perceptron, MLP)、自组织神经网络和卷积神经网络(Convolutional Neural Network, CNN)三种典型神经网络的发展现状，介绍神经网络识别加工特征的具体方法，包括特征预处理和编码，以及神经网络的实现过程，对比分析神经网络方法与其他特征识别方法及三种神经网络技术特点，并在此基础上展望神经网络识别加工特征技术的发展趋势。

1 三种神经网络概述

1.1 多层感知机

感知机是由Rosenblatt[7]最早提出的单层神经网络，是第一个具有学习能力的数学模型。但是单层的神经网络无法解决线性不可分问题，而随后出现的MLP却解决了这一问题。与单层感知机相比，MLP具有3个典型特点：① 输入层和输出层之间添加了隐藏层，且可以为多层；② 输出层的神经元个数可大于1个，一般情况下，用于预测和函数逼近的MLP的输出神经元为1个，用于分类的输出神经元为一个或多个，每一个表示一种类型；③ 隐藏层和输出层均含有非线性激活函数。

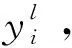
(1)

MLP的训练或学习方式属于监督型，其主要特点为：对于给定的输入信息，根据输出神经元的实际值和期望值之间的误差来调整隐藏层和输出层神经元间连接权值，使其最终满足总体计算误差要求。常用的训练方法有多种，例如反向传播(Backpropagation, BP)法、delta-bar-delta方法、最快下降法、高斯-牛顿法和LM方法等。实验结果表明，LM方法、高斯-牛顿法和最快下降法等训练速度优于BP和delta-bar-delta方法，其中LM方法最为有效[8]。

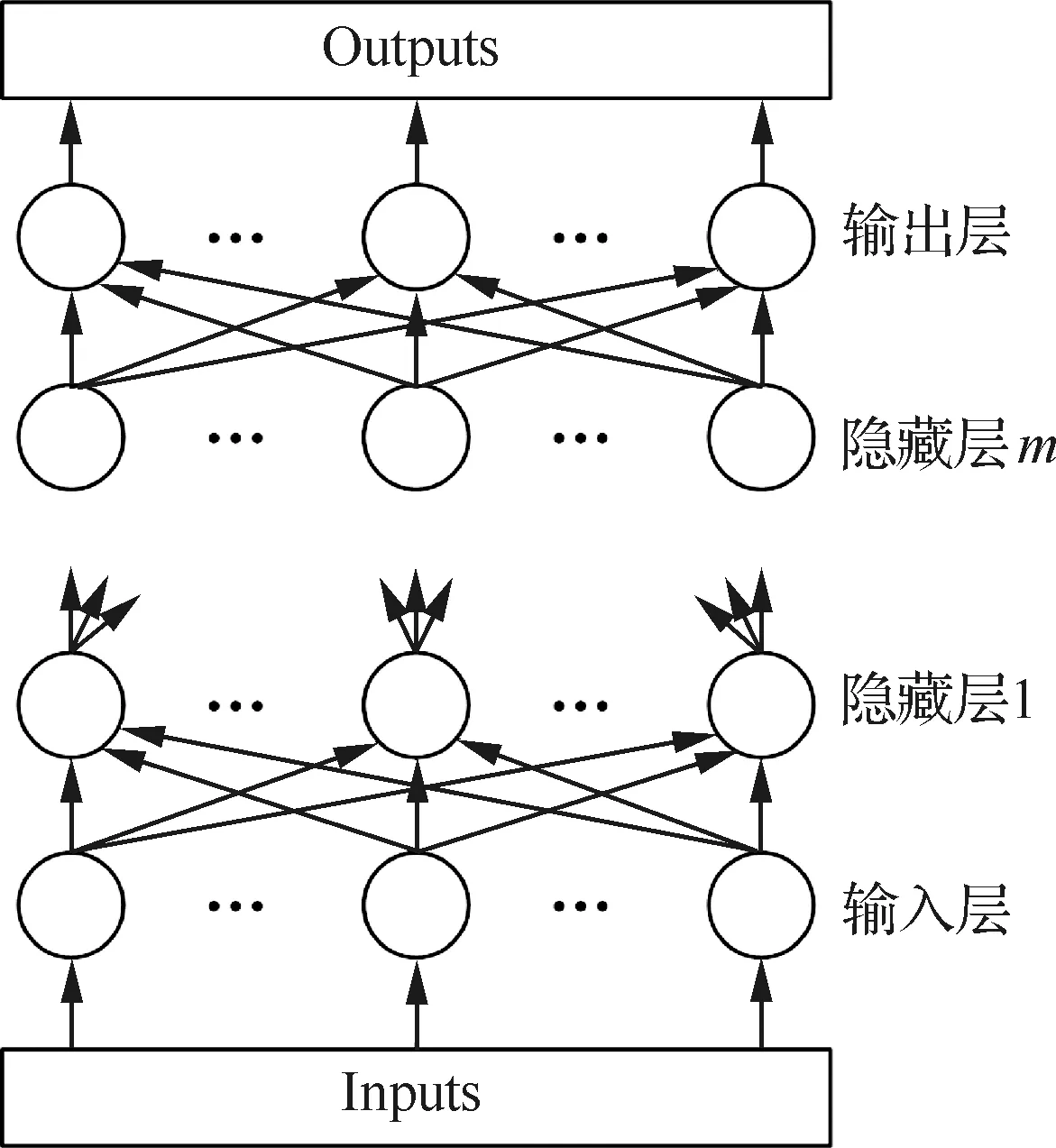
图1 MLP结构Fig.1 MLP structure

当MLP采用BP方法训练时，即为BP神经网络。BP方法是目前最常用的神经网络训练方法，其实质是计算误差函数的最小值问题，按照误差函数的负梯度方向修改权值。

BP算法包括信号正向计算和误差反向计算等两个计算过程。前面所介绍的计算过程即为信号正向计算，而误差E反向计算式为

(2)

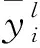
1.2 自组织神经网络

与MLP类似，自组织神经网络也是一种前馈神经网络。但是，自组织神经网络采用无监督学习方式，具有自组织学习能力，即自动学习输入数据中的重要特征或找出其内部规律，如分布和聚类等特征，根据这些特征和规律自动调整自身的学习过程，使得之后的输出与之相适应。对自组织神经网络来说，学习过程不仅包括网络参数的调整，也包括网络拓扑结构的调整。

在加工特征识别领域，已采用的自组织神经网络有自组织特征映射(Self-Organizing Feature Map, SOFM)和自适应共振理论(Adaptive Resonance Theory, ART)网络等。

SOFM是Kohonen于1981年提出的一个两层网络模型，其中第一层为输入层，神经元个数与样本维数相等；第二层为输出层，也称为Kohonen层。神经元排布有一维线性、二维平面和三维栅格三种形式，其中最常用的为二维平面形式。SOFM的神经元有两种连接关系：每个Kohonen层神经元与所有输入层神经元相连；Kohonen层的神经元之间互相连接，即侧向连接，这也是SOFM模仿大脑皮层神经侧抑制特性的一个体现。图2给出了SOFM的3种拓扑结构，其中圆/椭圆表示神经元，实线表示层间连接和输入/出，虚线表示Kohonen层内神经元间的连接。

图2 SOFM拓扑结构Fig.2 Topological structure of SOFM

对于一个给定的输入，SOFM通过竞争学习得到获胜神经元，之后获胜神经元与其附近的神经元(称为邻域)一起调整权值，该邻域特征有助于保持该输入的拓扑特性。

神经网络一般具有两种能力，可塑性是指网络学习新知识的能力，而稳定性则指神经网络在学习新知识时要保持对旧知识的记忆。通常，当一个神经网络对于输入样本的训练学习达到稳定后，如果再加入新的样本继续训练，前面的训练结果就会受到影响，表现为对旧数据、旧知识的遗忘。ART网络的建立即是为了解决神经网络这种可塑性与稳定性的矛盾。

ART理论由Grossberg于1976年提出，随后Carpenter和Grossberg[9]建立了ART网络，即ART1。ART1的输入被限定为二进制信号，使得其应用存在一定的局限性。ART2[10]作为ART1的扩展型，在网络结构上也进行了一定程度的改进，能够处理连续型模拟信号。ART1和ART2均为无监督学习类型，具有自组织能力，是ART网络中的最基本网络，在此基础上发展起来了兼容ART1与ART2的ART3、监督型学习的ARTM-AP、基于模糊理论的Fuzzy ART等。用于加工特征识别的ART网络有ART2和Fuzzy ART。

图3为ART2的基本构架，由监视子系统和决策子系统两部分组成。监视子系统包括比较层和识别层(Y层)及两层间的连接通路。其中比较层包含六个子层，分别为W层、X层、V层、U层、P层和Q层。决策子系统则由R层组成。ART2将相似的特征聚集在一起，特征的相似性则由警戒参数控制。当输入到网络的新特征与已存在的特征簇中的成员相似时，新特征就与该簇关联；否则，ART2为新特征创建一个新的簇。相关变量说明参见文献[11]。

图3 ART1构架[11]Fig.3 ART1 architecture[11]

1.3 卷积神经网络

CNN作为目前最著名的深度学习方法之一，已经在图像识别[12]、场景标记[13]、语音识别[14]、目标检测[15]、自然语言理解[16]等领域取得了突出的应用效果。CNN在处理和分析大型复杂数据方面具有很强的计算能力，并且由于具有良好的鲁棒性，CNN特别适用于视觉相关领域的特征提取和学习任务。

CNN的构架灵感来源于猫视觉皮层简单细胞和复杂细胞[17]的结构和功能。Fukushima和Miyake[18]建立的Neocognitron可被视为CNN的雏形，其框架由S-layer和C-layer交替组成。早期CNN的代表是LeCun[19-20]的LeNets系列，由卷积层(Convolution Layer, CL)和子采样层组成(见图4)。随着Hinton等[21]在2006年提出layer-wise-layer-greedy-learning方法，深度学习技术才得以真正意义上的建立和发展。2012年，Krizhevsky等[22]使用深度CNN模型AlexNet在ILSVRC ImageNet图像分类比赛中夺得冠军后，深度CNN的研究热潮席卷了整个计算机视觉领域，得到了广泛的应用[23-26]。

CNN一般由CL、池化层(Pooling Layer, PL)和完全连接层(Fully-connected Layer, FL)组成，CL与PL交替连接，FL多位于网络最后面。CL由多个特征图组成，每个特征图中的神经元都与前一层的神经元邻域相连，构成CL神经元的感受野，通过权值和激活函数提取感受野的特征。PL的目的是降低CL特征图的空间分辨率，从而实现对输入失真和平移的空间不变性，常用方法有平均值池化法和最大值池化法。FL可对网络中的抽象特征进行解释，并执行高级推理功能，实现分类和识别目的，常用的算子是softmax算子。CNN的结构决定了CNN有稀疏连接、参数共享和等价表示等三大关键要素。

Lin等[27]设计了一种Network in Network模型对CL进行改进，将一个传统的CL改为多层CL，从而将线性抽象转变为非线性抽象，提高了CNN的抽象表达能力。Zhai等[28]利用一个双CL替代单一的CL，用于平衡识别精度与内存占用量(即参数量)之间的关系。双CL的特点是其元滤波器的尺寸大于有效滤波器的尺寸。计算时，从每个对应的元滤波器中提取有效滤波器，之后将所有提取到的滤波器与输入连接进行卷积。

对于PL的改进，Krizhevsky等[22]提出了重叠池化方法，即相邻池化窗口之间存在重叠区域。由于同一个神经元可以参与不同的池化操作，因此可以在一定程度上提高识别结果。为了解决最大池化法容易陷入局部最优的问题，Sermanet等[29]建立了Lp池化方法，该方法可以通过随机表示将一般球分布扩展到范数表示，并估计最优非线性和子空间的大小。混合池化[30]是一种将平均池化法和最大池化法综合起来的池化方法，该方法既可以解决最大池化法因参数不均匀造成的失真问题，又可以避免平均池化造成的特征对比度下降的问题，但是该方法的训练误差较大。

图4 LeNet-5构架[20]Fig.4 LeNet-5 architecture[20]

传统的CNN采用的激活函数多为饱和函数，如sigmoid和tanh函数等。目前，不饱和激活函数成为主流，出现了ReLU[31]及其扩展函数。ReLU是一个分段函数，当x>0时，ReLU(x)=x；当x≤0时，ReLU(x)=0。ReLU的优点是可以帮助神经网络轻松获得稀疏表示。LReLU[32]的提出是为了改进ReLU在无监督预处理网络中的性能，采用的方法是当x≤0时，令LReLU(x)=αx，式中：α为比例因子，是一个给定值。LReLU的变体还包括PReLU[33]，其与LReLU的唯一区别是PReLU的α可以通过BP学习获得，且没有额外的过度拟合的风险。

2 神经网络识别加工特征

2.1 特征预处理与编码

加工特征存在于CAD实体模型中，包含几何和拓扑信息，而神经网络的输入形式是一组数值信息，也可称为表示向量(Representation Vector, RV)。因此，如何将CAD模型或加工特征转化为适用于神经网络的输入格式成为了神经网络识别加工特征的首要问题。本文将该问题表述为特征的预处理与编码问题。据文献，神经网络识别加工特征时，常用的特征预处理与编码方法主要有：基于属性邻接图(Attributed Adjacency Graph, AAG)编码、基于面邻接矩阵(Face Adjacency Matrix, FAM)编码、基于面值向量(Face Score Vector, FSV)编码、体素化方法和横截面分层法等。

2.1.1 基于AAG编码

加工特征的AAG通常定义为G=N,C,A，式中：N为顶点集，表示特征的组成面集；C为顶点间的连接边集；A为连接边的凹凸性集合。AAG只定义了模型的拓扑信息，不含有模型的几何信息。在基于AAG的编码中，为了获得作为神经网络的输入RV，需将AAG分解为AAG子图，再转化为邻接矩阵(Adjacency Matrix, AM)，然后根据AM得到RV。

通常，AM是一个二进制的对称矩阵，以对角线分为凸和凹两个区域，元素表示行列号所示的两个面的邻接边的凹凸性。取AM的上三角或下三角并按行列号依次排序，所得元素序列即为神经网络的输入[34]。

若各AAG子图的AM规格不一致，可对AM中的元素进一步提炼。首先建立一个有关拓扑与几何关系的问题表，然后根据AM确定各问题的二进制答案，最后将答案作为RV的各元素值。Nezis和Vosniakos[35]及Guan等[36]均采用该思路创建RV。

2.1.2 基于FAM编码

基于FAM编码是基于AAG编码的改进型，与AM相比，FAM增加了面的编码信息，因此能够更加准确地定义面间的邻接关系。FAM是一个对称矩阵A=(aij)m×m，其中aii表示第i个特征面的属性，aij(i≠j)表示第i个特征面与第j个特征面间的邻接关系，每种关系对应不同的整数值。FAM生成RV的方式与AM生成RV的方式相同。

Prabhakar和Henderson[37]建立了一个8×8的FAM，每一行/列定义为一个含有八个元素的整数向量，分别表示某个面与其邻接面间的属性，包括边类型、面类型、面角度类型、环个数等。该方法的缺点是不能分离拓扑相同但形状不同的特征。胡小平等[38]在添加虚构面的基础上设计了一个6×6的扩展型面邻接矩阵，以虚构的盒形体统一定义特征的表达式，并利用特征面的属性来区分特征的真实存在面和虚构面，避免特征的描述混淆。

考虑到AAG仅能识别平面和简单曲面特征，不能处理有共同底面的相交特征，Ding和Yue[39]建立了F-邻接矩阵和V-邻接矩阵。该方法通过一个空间虚拟实体(Spatial Virtual Entity, SVE)来表示初始模型生成最终特征时所需移除的实体。两种矩阵的实例如图5[40]和图6[40]所示。其中，F-邻接矩阵定义特征的组成面类型和面间的夹角，V-邻接矩阵定义SVE中虚拟面间的关系，即行列号对应的两个虚拟面是否相连。

图5 F-邻接矩阵实例[40]Fig.5 Example of F-adjacency matrix[40]

图6 V-邻接矩阵实例[40]Fig.6 Example of V-adjacency matrix[40]

2.1.3 基于FSV编码

面值计算公式是一个与面、边、顶点特征及其邻接关系有关的函数[41]，用FSV对特征进行编码的常用思路为：① 定义FSV的计算式及各分量的分值表；② 定义RV的元素个数和相应的面顺序；③ 根据公式计算各特征面的值；④ 将各面值作为元素值生成RV。

FSV的计算公式可概括为F=G′+L+E′+V，F为面分值；G′为面几何分值，表示面的凹凸性；L为环值；E′为边值；V为顶点值。通过对相关文献的研究，该公式有以下几种表现形式：

1)F=G′+L+V型

该类型的FSV包含面几何分值、环值和顶点值等三个参数，其中面几何分值与环值由分值表查询获得，顶点值则与过该点的边值有关。相关实例包括文献[42-44]等。

2)F=G′+V型

该类型的FSV包含仅包含面几何分值与顶点值两个参数。Marquez等[45]采用该公式定义FSV，并用数值的正负表示面、边等元素的凹凸性。Sunil和Pande[46]采用该方法计算面分值，并将特征的7个组成面的面分值作为输入RV的前7个元素值。

3)F=G′+E′+V型

Öztürk和Öztürk[47-48]采用该公式将特征定义为一个关于点、边和面的输入矢量，这种方法的局限性是仅能表示有限的复合特征，并且特征样本和特征之间不含一一对应的关系。

4)F=G′+L+E′+V型

Jian等[49]建立的面值计算公式为

(3)

式中：Ai为特征面的分值；Fi为面的权值，定义面的凹凸性；Eij为环的权值；Lik为边的权值；Vix为邻接关系权值，定义特征面与邻接面的夹角关系，其目的是帮助识别V型槽等具有特殊夹角的特征；m′、n′和q分别为相应的对象个数。

2.1.4 体素化方法

体素化方法是三维CNN特有的特征预处理与编码方法，通过将CAD模型划分为体素网格，对体素进行二进制赋值，进而获得CNN的输入数据。以图7为例[50]，若体素位于模型内部则赋值1，即绿色点集，若体素位于模型外部则赋值0，即红色点集。通过这种方法，整个模型可以表示为一长串二进制数字，便于CNN进行卷积计算。

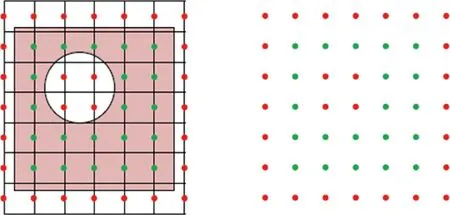
图7 CAD体素模型的可视化[50]Fig.7 Visualization of voxelized CAD models[50]

体素化的方式包括渲染法[51]和奇偶计数法与射线穿透法相结合的方法[52]。为了加速体素化过程，Balu等[50]利用图形处理单元划分体素网格，比CPU方法快10倍以上，而且能够创建超过10亿个体素的CAD体素模型。为了减少特征边界信息的丢失，Ghadai等[51]利用面法线嵌入网格的方式来增强体素化过程。

2.1.5 横截面分层法

横截面分层法[53-54]是指对于具有相同厚度和公共底面的相交特征，采用分层方法得到实体模型的二维合成区域，从而将三维特征属性转为二维特征属性，合成区域的各顶点信息即为神经网络(如SOFM)的输入。

图8给出了一个由实体模型(见图8(a))生成合成区域的具体过程，在模型的顶点处逐层切片，获得一系列相互平行的横截面图(见图8(b))后，利用横截面间的减法处理得到合成区域(见图8(c))。相关变量说明参见文献[53]。

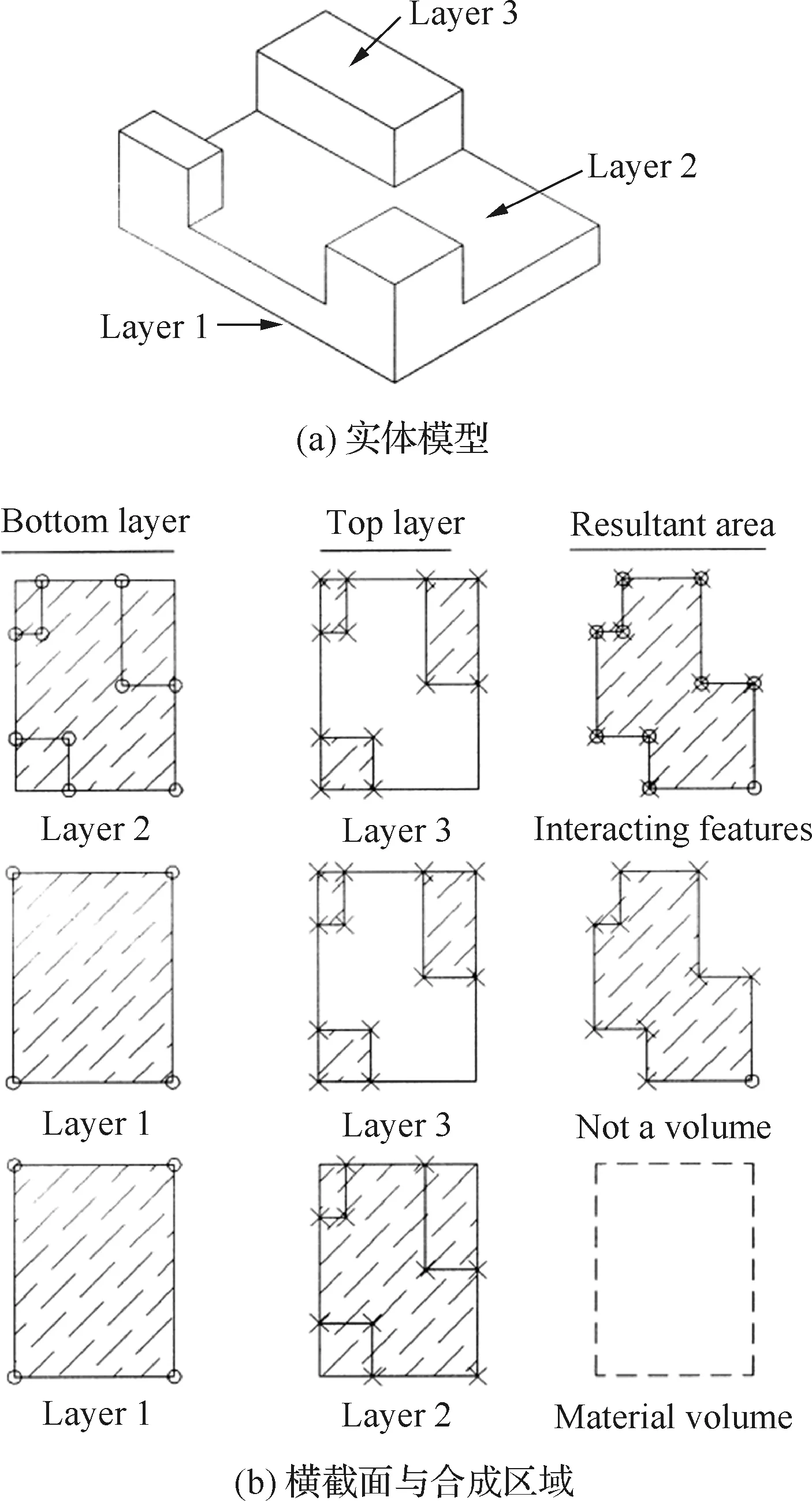
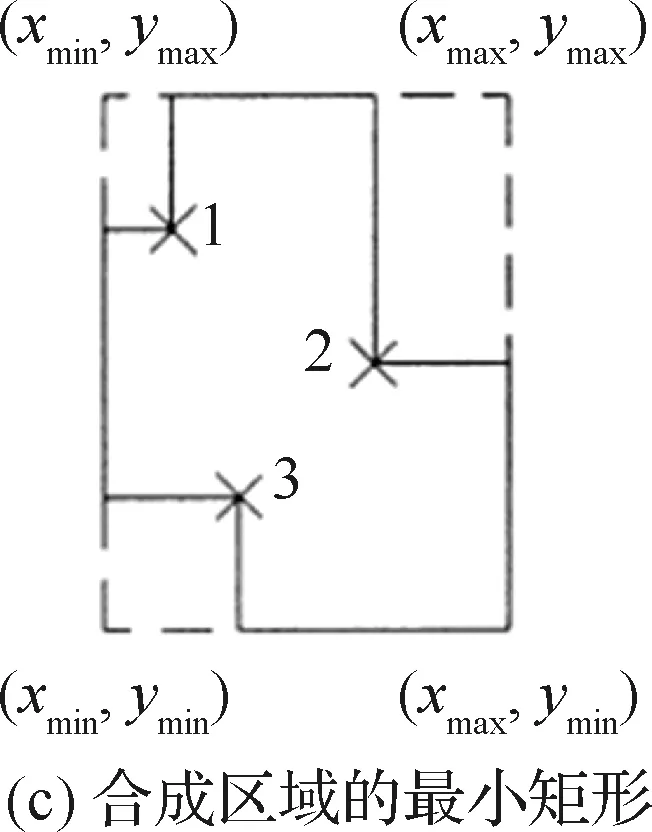
图8 相交特征的分层方法[53]Fig.8 Layering technique used to find interacting features[53]

2.2 神经网络结构

神经网络创建包括三方面的设计：网络参数设计、数据集构建和训练方法选择。面向加工特征识别任务时，神经网络的数据集为CAD实体模型，网络参数和训练方法则根据识别对象的复杂程度和特点进行配置与设计。

2.2.1 网络参数设计

MLP参数设计主要包括层数选择以及层的结构设计。虽然目前并没有明确的设计准则来辅助结构参数的设计与选择，但是有学者研究发现对于MLP，三层结构足以解决一般性的非线性映射问题，并且能够满足要求的准确度[55]。

隐藏层是MLP的设计难点，隐藏层神经元的数量过多会使数据过拟合，造成网络泛化能力的松散；隐藏层神经元个数较少则会影响网络的学习能力。比较保守的方法是将隐藏层神经元个数介于输出神经元数量和输入神经元数量之间。

表1和表2分别列举了加工特征识别常用的两种MLP网络结构，即三层MLP和四层MLP。其中三层MLP各层的神经元个数分别为n1-p1-q1，四层MLP各层的神经元个数为n1-p1-p2-q1，表中的参数个数是指对一个样本执行前馈计算时的计算参数量。通过两表可得以下规律：① 对于三层MLP，p1与n1无绝对的大小关系，通常p1∈[n1,2n1]；② 四层MLP中，一般选择p1=p2，其目的是简化神经网络计算；③ 对比文献[56]和文献[47]可知，在n1与q1基本保持不变的情况下，将一个隐藏层分解为两个隐藏层可以显著减少参数个数；④ 三层MLP的时间复杂性可表示为O(n1p1+p1q1+p1+q1)，分别改变n1和p1时，时间复杂度的变化分别为O(Δn1p1)和O(Δp1(n1+q1+1))，显然隐藏层神经元个数的变化对时间复杂度的影响较大。

表1 三层神经网络构造Table 1 Three-layer neural network configuration

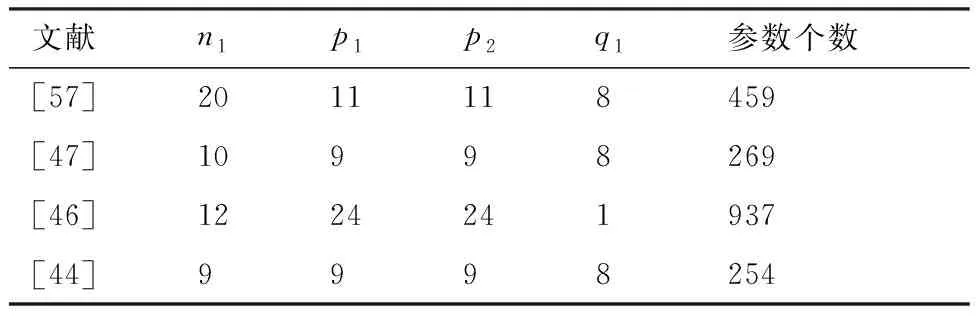
表2 四层神经网络构造Table 2 Four-layer neural network configuration

SOFM网络设计主要包括神经元的个数设置和邻域的尺寸设计。为了识别九种加工特征，Onwubolu[43]建立了一个输入层有10个节点，Kohonen层有100×100个节点的SOFM，邻域大小为5。结果显示，SOFM迭代后可以识别不同类别的特征，且槽和台阶两种特征被聚为一类。文献[53-54]将多级SOFM用于相交特征中相交区域的分解，每一级的输入都是当前合成区域的各顶点，输出均为2×2数组。

CNN的结构设计包括各类型层的选择以及过滤器的尺寸设置。其中，常见的类型层包括CL、PL、FL和输出层(Output Layer, OL)等。为了确定钻孔特征的可加工性，Balu等[50]建立了一个7层的三维CNN，如图9所示，依次包括输入层→CL(8×8)→PL→CL(4×4)→PL→FL(10)→OL(2)。OL的2个神经元分别表示可加工和不可加工。Ghadai等[51]对上述模型进一步修正，在CL和PL后添加了一个批量标准化层，目的是改善网络的饱和现象进而提高实验精度。

FeatureNet[52]是第一个将深度学习应用于加工特征识别的三维CNN。FeatureNet的结构如图10所示，包括4个CL、1个PL、1个FL和1个OL。多个CL的连接有助于对复杂的结构特征分层编码和识别。OL含有24个神经元，每个神经元代表一种特征。整个网络拥有3 400万个参数，远远超过MLP的参数量。相关变量说明参见文献[52]。

图9 三维CNN[50]Fig.9 3D CNN[50]

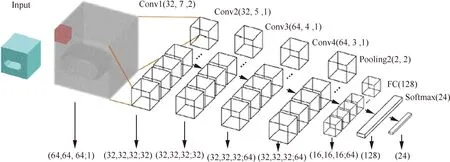
图10 FeatureNet结构[52]Fig.10 FeatureNet structure[52]

2.2.2 数据集构建

前文提到的三种神经网络中，MLP和CNN属于监督型网络，自组织神经网络为无监督网络。监督型神经网络需要依赖有标签的数据进行训练，借助标签数据的期望输出来修正权值，调整特征。这种微调建立在大量标签数据的基础上，而未标注数据对监督型训练的作用不大。但是，神经网络很难获得足够多的标签数据来拟合一个复杂模型，因此标签数据的获取是神经网络训练的一个难点。创建数据集和迁移学习是数据获取和扩容的常用方法。

根据文献，加工特征数据集由一系列CAD 3D模型组成，每个模型一般仅包含一个加工特征，同一类型的加工特征在形状、位置和尺寸(如半径、高度、长度等)等方面有所区别，数据集实体模型的类型与神经网络待识别的特征类型相对应。图11为文献[36]创建的训练样本，每一类样本都有各自的输入矢量与期望输出矢量，元素均用二进制数字表示。相关变量说明参见文献[36]。

一个完整的数据集应包括训练集、测试集和验证集三部分。其中，验证集用于调整网络超参数，不参与最终测试。Ding和Yue[39]建立了一个分层的神经网络系统，将137个训练实例和15个测试实例用于第一级网络后，又将62个训练实例用于专门识别槽/台阶面的神经网络，并用12个模型样本进行测试。Sunil和Pande[46]选择了95个实例模型用于训练，20个实例模型用于测试。

与MLP相比，CNN的参数量成数量级倍增加，因此需要规模更大的数据集。Balu等[50]为CNN建立了6 669个正方体模型，每个模型仅包含一个钻孔特征，且孔的直径、深度、位置等在规定范围内变化。模型尺寸均为5英寸。50%的模型作为训练实例，25%的模型作为验证实例，其余的作为测试实例。Zhang等[52]为CNN建立了一个更大规模的数据库，存储了24种特征(见图12)，每种特征含有6 000个不同的样本模型。这些模型均为统一规格(10 cm)的正方体结构。

图11 训练样本的输入与输出[36]Fig.11 Input and output of training samples[36]

随着深度CNN的迅速发展，大型数据集对CNN的影响和作用越来越明显，更加凸显了数据集创建的必要性。对于一些很难获得的标签样本，迁移学习是数据集扩充的一种有效方法。迁移学习是一种运用已有知识对不同但相关领域问题进行求解的机器学习能力，常用的一种方法是对预训练模型进行微调。例如，Shin等[58]对AlexNet和GoogLeNet微调时，将CNN所有层(不含最后一层)的学习速率由默认值减小了10倍。Han等[59]仔细研究了预训练网络的超参数调整，利用贝叶斯优化来处理学习率的搜索问题。

图12 24种加工特征[52]Fig.12 24 manufacturing features[52]

2.2.3 训练方法选择

神经网络最常用的训练方法为BP算法，文献[10,19,46]等均采用此方法。然而，该方法存在一定的局限性，收敛速度慢和容易陷入局部极小是其中的两大问题。目前针对BP算法的改进措施中，动量法是较常用的一种方法。通过在原来的权值调整公式中增加一个含动量比的乘积项，能够减小学习过程中的振荡趋势，降低网络对误差曲面局部细节的敏感性，从而改善收敛性，抑制网络陷入局部极小。

Ding和Yue[39]采用了共轭梯度算法训练神经网络，该方法在一组相互共轭的方向调整权值，与最快梯度方向相比能获得更快地收敛。Shao等[60]选择粒子群算法训练MLP，初始化一群“粒子”后通过迭代寻找最优解，迭代过程中不断更新粒子本身的最优解和全局最优解。该方法的优点是收敛快，精度高。Jian等[49]设计了一种新型蝙蝠算法(Novel Bat Algorithm, NBA)训练BP神经网络，与粒子群算法相比，该方法能够控制局部搜索与全局搜索之间的转换，避免网络陷入局部最优缺陷，有助于提高特征识别的准确性。

警戒参数ρ是ART2计算过程中的一个重要参数。ART2将相似的特征聚集在一起，特征的相似性则由警戒参数控制。当网络新输入的特征与特征簇中的已有成员相似时，新特征就与该簇关联；否则，ART2为新特征创建一个新的簇。一般情况下，随着警戒参数的提高，ART2的聚类由粗糙转向精细化，这种现象在Fuzzy ART[61]中也得到了验证。随着警戒参数ρ依次选择为0.85、0.95、0.98和0.99，五种特征由共享一个簇发展为拥有各自的簇(见图13)。

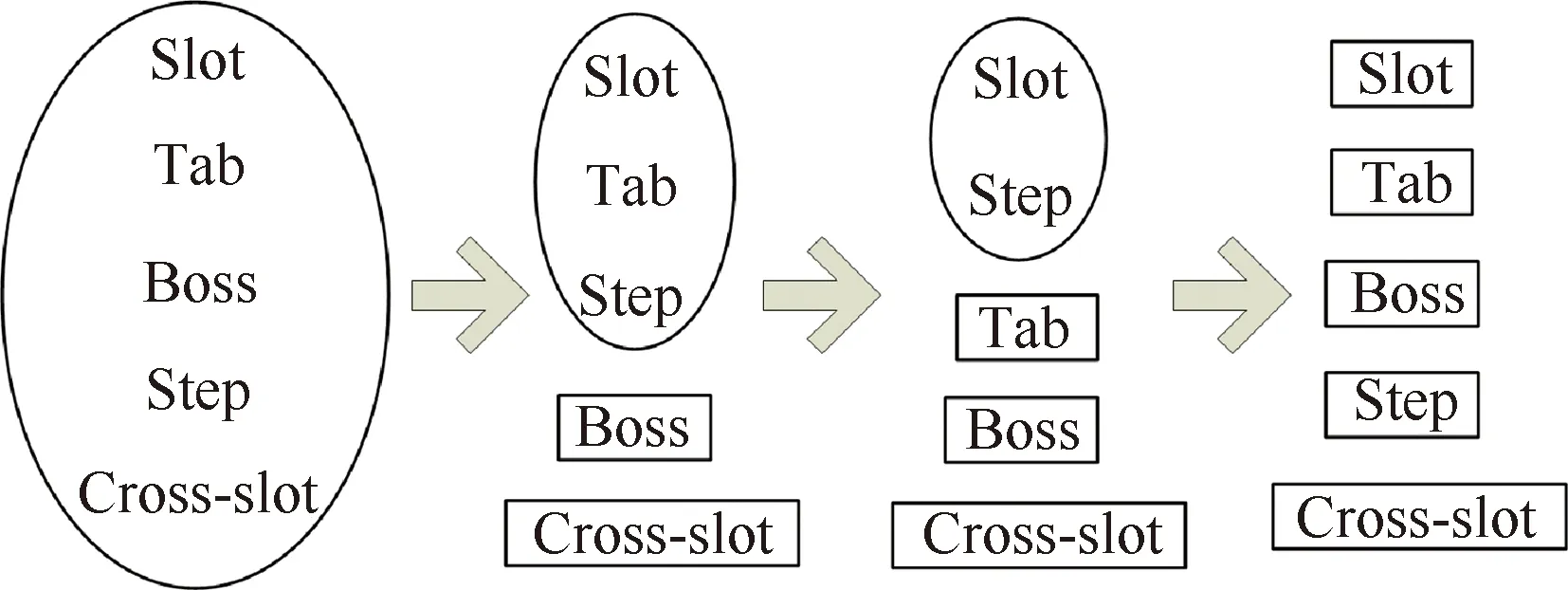
图13 Fuzzy ART分类Fig.13 Fuzzy ART classification

3 对比分析

3.1 神经网络方法与传统方法

近30年来，有关加工特征识别的研究已经相当成熟，并形成了多种不同类型的识别方法，每种方法都有各自的优势和不足。

基于图的方法具有特征定义简单，算法效率高，能准确描述特征面邻接属性等优点，但是该方法识别相交特征时易丢失邻接关系。基于体分解的方法不受特征拓扑结构的限制，能够较好地处理相交特征的识别，然而识别过程依赖大量的布尔运算，导致计算量大、算法效率低下。基于规则的方法在特征表示方面具有很好的性能，但是对每种特征都进行规则预定义是不现实的，故该方法灵活性较低。此外，拓扑或几何变形可能会使简单特征的规则描述过于繁琐，造成计算成本较高[62]。基于痕迹的方法多以几何与拓扑信息作为痕迹进行识别，当痕迹指向多种特征时，需要进一步的几何推理来获得所需特征。该方法虽然可以有效地识别相交特征，但是当痕迹的数量明显多于特征时，可能会导致无效的特征或特征被其他特征所覆盖[63]。

与这些主流的识别方法相比，神经网络识别方法具有以下几点优势：① 具有学习能力[64]，能够隐式推导特征的构造关系，识别和分类具有不同尺寸和拓扑的相似特征；② 具有泛化能力，通过训练可以识别预定义的一组特征，进而可扩展到识别新的特征；③ 训练完成后可保持很高的处理速度；④ 抗噪性能好，有利于识别相交特征。

然而，神经网络方法识别加工特征仍然存在着一些不足：① 神经网络输出层的神经元个数一般为待识别的特征类型数，但是中间各层的结构配置方法还需进一步研究；② 加工特征数据集的样本模型结构简单，只包含一个特征，且多为标准特征，不含有相交特征；③ 加工特征识别前需要将其转换为数值表示，转换过程中容易造成特征某些信息的丢失，影响识别精度。

表3对比了不同特征识别方法的识别范围。

表3 特征识别方法与识别范围

Table 3 Feature recognition methods and their recognition range

识别方法识别范围基于图独立特征基于体分解独立特征,有限个相交特征:仅含柱面和平面基于规则独立特征,预定义的相交特征基于痕迹尺寸适中的独立特征,相交特征神经网络独立特征,相交特征

3.2 不同神经网络方法

本节针对三种神经网络方法，分别从输入特性、输出特性、识别范围和相交特征处理等几个方面分析各自的特点。

3.2.1 输入特性

一种合理且有效的特征预处理与编码方法必须具备三点特性：① 能够准确且完整地表达加工特征的几何与拓扑信息；② 能够被输入层识别，符合RV的要求；③ 每一类特征都有唯一的表示，各类特征间的表示不重叠。

根据组成元素类型，RV可分为三种：① 整数型，即元素均为整数；② 实数型，即元素均为实数；③ 二进制型，即元素仅有0和1两种值。通常，基于AAG和FAM编码的RV多为整数型或二进制型，基于FSV的RV元素多为小数，体素化方法得到的体素网络均用二进制表示。

表4总结了三种神经网络常用的特征预处理与编码方法。由于特征具有复杂的拓扑与几何特性，因此综合了面、环、边和点信息的面编码方式比AAG编码方式更准确，也更有效。自组织神经网络的输入同样依赖CAD模型的B-rep信息提取和特征表达方法，因此，能够更好反映拓扑信息的特征表达方法对提高自组织神经网络的稳定性和鲁棒性具有重要意义。

关于CNN的输入类型，一方面，CNN的体素化表达是一种与几何信息无关的数值转换，而其他两种神经网络从B-rep模型提取几何信息，并借助预定义的公式生成RV；另一方面，CNN直接选择体素(三维形式)作为输入，与将三维对象简单投影到二维表示(如深度图像或多视图等)相比，既可减少几何特征的丢失，又可避免局部或内部特征不易投影的问题。

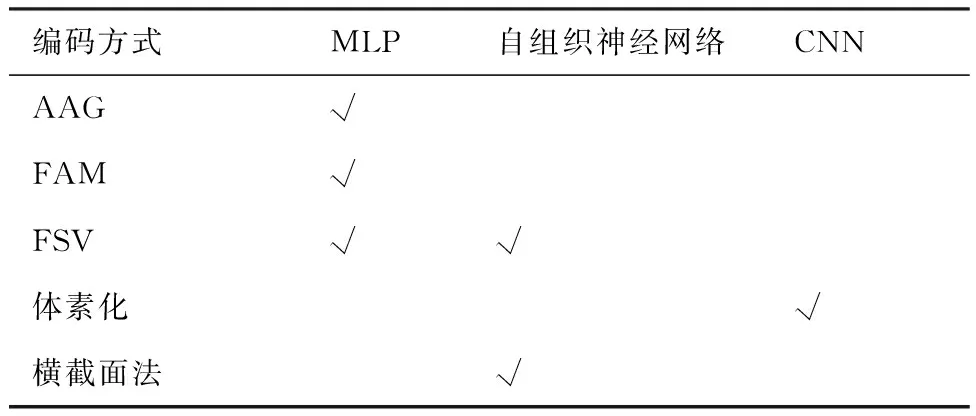
表4 三种神经网络的常用编码方法

3.2.2 输出特性

神经网络的输出是神经网络的输入与权值反复计算和相互作用的结果，从形式来看，神经网络的输出有以下几种形式：① 单个神经元的输出；② 向量形式的输出；③ 矩阵形式的输出。

文献[45-46]属于单个神经元的输出形式。其中文献[45]为每一种特征建立了一个三层MLP，其输出为一个二进制数值，用于表示该类型特征的识别结果。文献[46]的输出值是一个实数值，且不同的数值代表不同的识别类型，如 0.10 代表三角形型腔，0.12代表长方形型腔等，所有特征类型的输出值位于区间[0.1,0.8]。

向量是最常见的神经网络输出形式，可分为二进制形式的向量和实数值形式的向量。在二进制型向量中，若每个神经元对应一种类型的加工特征，且每次仅激活一个输出神经元，则该向量为one-hot向量。文献[34,36,39]等均采用该输出方式。文献[49]虽然也是二进制向量输出，但是存在两个神经元同时激活一种特征的情况，如[0,1,1]表示通槽，因此不属于one-hot向量。实数型向量的代表有文献[52]等。此外，Hwang和Henderson[41]应用了含六个元素的输出向量，每个元素分别代表类、名称、置信因子、主面名称、关联面列表以及总执行时间。

矩阵也是神经网络输出的一种形式，文献[53]建立的SOFM的输出即为一个二进制矩阵O=[bij](i=1,2;j=1,2,3,4,5)，其中b1j代表识别的特征代码，b2j表示该特征在五个坐标轴方向上的可加工性。

总之，二进制向量形式是最常用的神经网络输出形式，若采用one-hot编码，每次计算仅有一个输出神经元被激活，因此特征类型数即为输出向量的元素个数。以3种特征为例，one-hot编码需要3个输出神经元，而非one-hot编码仅需2个神经元，可表示为[0,1]、[1,0]和[1,1]，由此可见one-hot编码在一定程度上增加了神经网络的参数量，表1中文献[49]和文献[56]的对比也反映了这个问题。

3.2.3 识别范围

由于神经网络类型的不同，特征预处理方式的不同，以及训练方法等的不同，加工特征识别的范围也不尽相同。本文对相关文献进行了详细的分析，并列举了部分文献识别加工特征的范围和优缺点，相关内容见表5，其中I级特征与II级特征的说明见3.2.4节。

由表5可知，槽、台阶、型腔、孔等简单特征最易识别，相交特征特别是II级相交特征是各种神经网络识别的难点。近年来随着研究的深入，相关算法也在进一步发展。遗传算法、NBA算法等其他技术被应用到MLP中，提高了识别性能，然而识别范围并没有明显的扩展。深度学习技术虽然是加工特征识别的新方法，但在识别范围和精度方面均有明显优势，由此也体现了以CNN为代表的深度学习方法在加工特征识别领域的潜在能力。

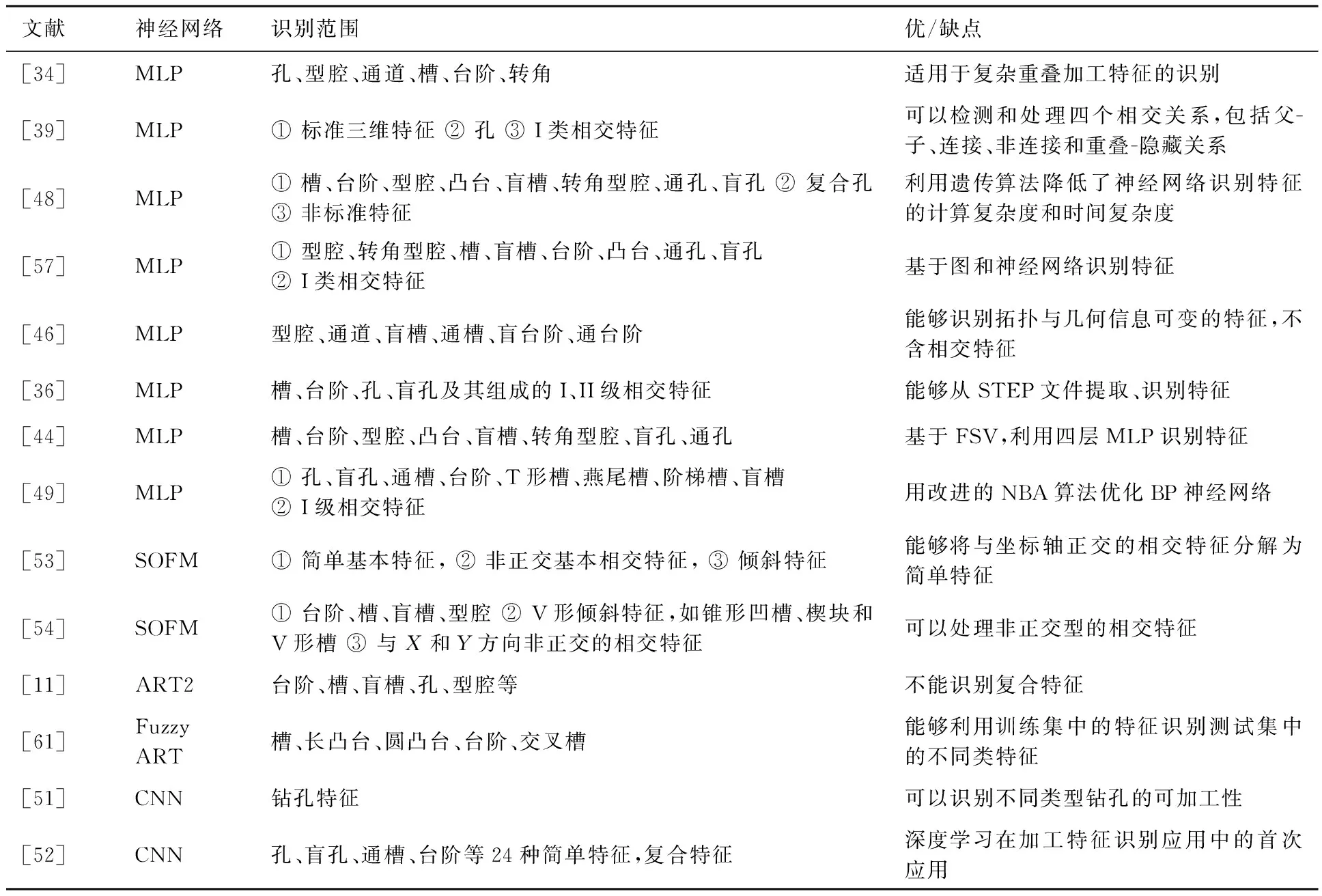
表5 基于神经网络的特征识别方法Table 5 Feature recognition methods based on neural networks

3.2.4 相交特征处理

相交特征识别一直是特征识别的难点，复合/相交特征存在两种形式的特征交叉。在第一种形式中，简单特征的内部面同时是其他简单特征的外部面，这种复合特征能够分解出多个完整的简单特征，可称为I类相交特征。另一种特征交叉中，两个或多个简单特征具有共同的面，且这些面均位于特征的内部，该类型的特征不能分解出相互独立的子特征，可称为II类相交特征。神经网络识别相交特征具有一定的优势，其主要原因是神经网络具有良好的抗噪性，当输入特征为相交特征时，神经网络通过训练可在一定程度上学习相交特征的主要特点，忽略次要信息，进而识别得到正确结果。常见的相交特征处理方法可归结为分解子图法、启发式算法、横截面分层法和基于软件包的方法等，其中：

1) 分解子图法

基于AAG和FAM编码的神经网络识别复合特征时，通常先生成模型的AAG，然后再用启发式算法或其他方法生成子图，每个子图只包含一个简单特征，最后将子图转为神经网络的输入。文献[36]即用这种方式处理相交特征。

对于一些复合特征，如多级孔等，子图分解方法可能会将其分为多个子特征。然而，考虑到特征间的相互作用，这些子特征应被识别为一个统一的整体。为了解决此问题，文献[49]对子图分解后得到的任意两个AM(特征因子)进行比较，若存在公共面和公共基面，则将这两个特征因子组合为一个特征。

2) 启发式算法

启发式算法识别相交特征的基础是利用相交特征对构建不同类型的相交实体(Interacting Entity, IE)。首先遍历模型中的所有特征，然后对每个特征对执行布尔交叉运算，最后分析IE，从而确定每对特征的关系。具体算法可参见文献[39]。文献[35]利用启发式算法将复合特征分解为简单特征，之后输入神经网络进行识别，但是该方法不能处理II类相交特征。

3) 横截面分层法

文献[53-54]识别相交特征时，利用横截面分层的方法获取相交区域的顶点，然后用SOFM进行聚类，结合布尔运算分解相交区域和提取体积数据，实现整个相交特征合成区域的分离。根据相交区域的复杂程度，该过程可能需要执行多次SOFM操作。

4) 基于软件包的方法

FeatureNet[52]使用Python的scikit-image包中提供的连通分量标记算法，先将不相邻的特征或特征子集彼此分离，再利用分水岭分割算法将每个分离的特征子集分割为单个特征，最后输入到CNN进行识别。

4 展望

神经网络识别加工特征是同时利用和融合了神经网络学习特性和CAD/CAM/CAPP专业属性，是一种完全有别于传统识别方法的跨学科技术。其可能的发展趋势如下：

1) 深度学习算法应用。目前，CNN已经被初步应用到加工特征的识别中，但是采用的结构简单，数据集的规模也较小。未来可以考虑模仿AlexNet、VGGNet等深层网络结构建立更加复杂的CNN模型识别加工特征。同时，鉴于ImageNet对分类和识别任务的重要性，有必要建立一个种类多样、模型复杂、尺寸变化大、形状不规则的CAD模型数据集，为神经网络训练和测试提供数据。此外，体素化方法在边界特征表示、计算效率等方面还不太完善，也需进一步优化和思考。

2) 全信息特征识别。从CAD/CAM/CAPP角度考虑，为了保证下游CAPP模块或检查和装配过程规划中能够获得有效的特征，特征识别系统除了能够识别形状特征外，还应找到零件的特征和相应的尺寸及公差之间的匹配关系，具体涉及尺寸、几何公差、形位公差及其他特征属性等。因此需要研究神经网络对多种不同类型属性的识别问题，以及建立配套的特征表示方法。

3) 类人脑认知结构。神经网络的本质是基于数据驱动的数值计算方法，因此任何类型的神经网络识别加工特征都须将CAD模型转换为数值输入。神经网络是对大脑系统的模仿和再现，同样地，利用类人脑技术模仿大脑的某些机理，也可以建立新型的神经网络。其中的一种构思是将网络设计为与传统神经网络类似的结构形式；在输入类型上直接以面作为输入，不必转换为数值信息；神经元处理函数不再是数值型的激活函数，而是自定义的认知表达式形式。此时的神经网络可转变成一种基于逻辑运算的神经网络。这也是神经网络在3D模型的面特征识别领域的一个发展方向。