翼身融合布局民机克鲁格襟翼设计
2019-09-25张明辉陈真利毛俊王刚谭兆光王龙张彬乾
张明辉,陈真利,*,毛俊,王刚,谭兆光,王龙,张彬乾
1. 西北工业大学 航空学院,西安 710072 2. 中国商用飞机有限责任公司 上海飞机设计研究院,上海 201210 3. 航空工业 惠阳航空螺旋桨有限责任公司,保定 071051
翼身融合 (Blended-Wing-Body,BWB) 布局以其突出的综合性能优势,满足以减少油耗、排放、噪声为主要目标的“绿色航空”发展要求,得到重视和迅速发展[1-2]。随着研究工作的深入,BWB布局低速起降性能较差的问题逐渐凸显,成为阻碍其工程化发展的技术瓶颈之一[3-4],BWB布局增升装置设计成为亟需解决的关键技术。
增升装置设计始终是民机气动设计的关键问题之一,经过国内外的长期研究,以前缘缝翼和后缘开缝襟翼为代表的传统增升装置设计技术与方法等较为完善[5-7]。但是,BWB布局对增升装置设计提出了新的问题与挑战。传统增升装置不适用于BWB布局主要有两方面原因。其一,传统增升装置尤其是前缘缝翼不适应层流技术的使用需求。采用混合/自然层流技术进行机翼设计,可减少10%的阻力并降低5%的燃油消耗,是提高民机经济性的有效手段[8]。BWB布局作为未来民机先进布局,欧美多个研究项目[9-11],如ERA、SUGAR、ACFA2020等均明确表示其BWB布局机翼计划采用混合/自然层流技术。层流技术要求保证机翼前缘尤其是上表面的连续性,以避免引起过早转捩,影响层流设计效果。而前缘缝翼不可避免地会破坏机翼上表面的连续性,因此不是BWB布局前缘增升装置的最佳选择。其二,BWB布局翼身高度融合,布局自身存在纵向操纵舵面力臂较短、配平效率不高的先天不足。传统的三段式增升装置虽然增升效率高,但附加力矩较高,增升状态下难以配平,纵向控制舵面设计压力大,因此难以应用于BWB布局。新型主动流动控制手段,如吹气襟翼或边界层抽吸等方法可以提高低速性能,但实际应用中在重量、安全可靠性、复杂度与费效比等方面仍存在问题。克鲁格襟翼(Krueger Flap)以其独特的运动机构形式受到BWB布局的青睐。克鲁格襟翼布置于机翼前部下表面,采用沿前缘旋转式运动机构,可以避免破坏翼型前缘与上表面的连续性;起降阶段,展开的克鲁格襟翼不但具有增升效果,还对机翼前缘有遮蔽效果,可防止昆虫与尘埃沾染,适用于层流机翼设计[12-13]。
克鲁格襟翼并不是崭新的概念,其发展过程曲折。Krueger[14]于1947年首次提出克鲁格襟翼的概念。1970年,Boeing通过四铰链机构实现变弯度克鲁格设计[15],但最终因较高的复杂度和昂贵的制造和维修费用而停止使用。此后克鲁格襟翼发展基本停滞,直到层流技术与BWB布局等未来民机对增升装置新需求的出现,克鲁格襟翼研究逐步苏醒。Rudolph[16]提出在折叠钝头克鲁格襟翼上应用缝道效应以代替缝翼的控制效果,并于1999年在B747混合层流技术验证机上进行了飞行试验[17]。Wild等[18-20]在DeSiReH项目(2009—2013年)中在常规布局基础上开展层流机翼的增升装置设计,试验表明开缝克鲁格襟翼增升效果与前缘缝翼相近。Akaydin等[21-22]的研究进一步表明,通过几何形状与缝道参数变化,克鲁格襟翼能取得不同偏度缝翼的增升效果。Vicroy等[23]基于折叠钝头克鲁格襟翼概念,对ERA BWB布局进行了前缘增升装置设计,并开展了低速试验。
由上述研究现状可知,克鲁格襟翼设计细节变化多,不同研究中克鲁格襟翼外形差异较大,并且研究主要关注于气动特性,对流动形态与增升原理分析并不深入。参考克鲁格襟翼发展历程并结合工程实用性,本文以开缝刚性钝头克鲁格襟翼作为研究对象,首先,建立了二维参数化建模方法,准确描述几何外形与缝道配置,获得参数变化对流动特征与气动性能的影响规律;并根据工程设计约束,提出克鲁格襟翼设计原则。其次,根据设计原则对参数设计空间进行减缩,提出开缝刚性钝头克鲁格襟翼的设计思想,并开展优化设计,得到增升能力强、失速特性好的二维克鲁格设计方案。随后,将设计方法应用于BWB布局,分析克鲁格襟翼三维流动形态与气动特性。最终,给出前缘开缝刚性钝头克鲁格襟翼、后缘简单襟翼的BWB布局增升方案,并通过风洞试验进行性能评估与验证。
1 研究方法
1.1 二维数值方法验证
本文首先验证用于模拟二维增升装置流动问题的数值模拟方法的可靠性及计算精度。采用典型的30P30N三段翼型[24], 前缘缝翼参数配置为偏度δs=-30°,缝道宽度Gs=2.95%c,重叠量Os=-2.5%c;后缘襟翼缝道参数配置为偏度δf=30°,缝道宽度Gf=1.32%c,重叠量Of=1.0%c;c为干净翼型弦长。为保证计算精度,采用C型拓扑的多块结构网格划分策略,近壁面网格保证无量纲高度y+≤1,远场大于25倍参考弦长。为更好地模拟多段翼型绕流的多种复杂流动现象,分别对前缘缝翼尾迹流区、缝翼凹角区、襟翼凹角区、各翼段边界层、主翼及襟翼上方尾迹/边界层掺混区等关键区域进行了网格加密处理,以便更好地捕捉这些区域的流动细节,网格总数为20万,如图1所示。
数值模拟的控制方程为雷诺平均Navier-Stokes方程,采用有限体积法进行离散,隐式二阶迎风格式时间推进,多重网格技术加速收敛,剪切应力输运(SST)k-ω湍流模型,残差收敛精度为10-6。图2和图3给出了雷诺数Re=9.0×106、马赫数Ma=0.2时,数值计算(CFD)与风洞试验(Test)的升力系数CL及压力系数Cp分布比较,图中α为迎角。可以看到,两者吻合良好。表明本文所采用的CFD方法具有较高的精准度,可以用于增升装置研究。

图1 30P30N翼型C型拓扑计算网格Fig.1 C-topologized computational grid for 30P30N airfoil
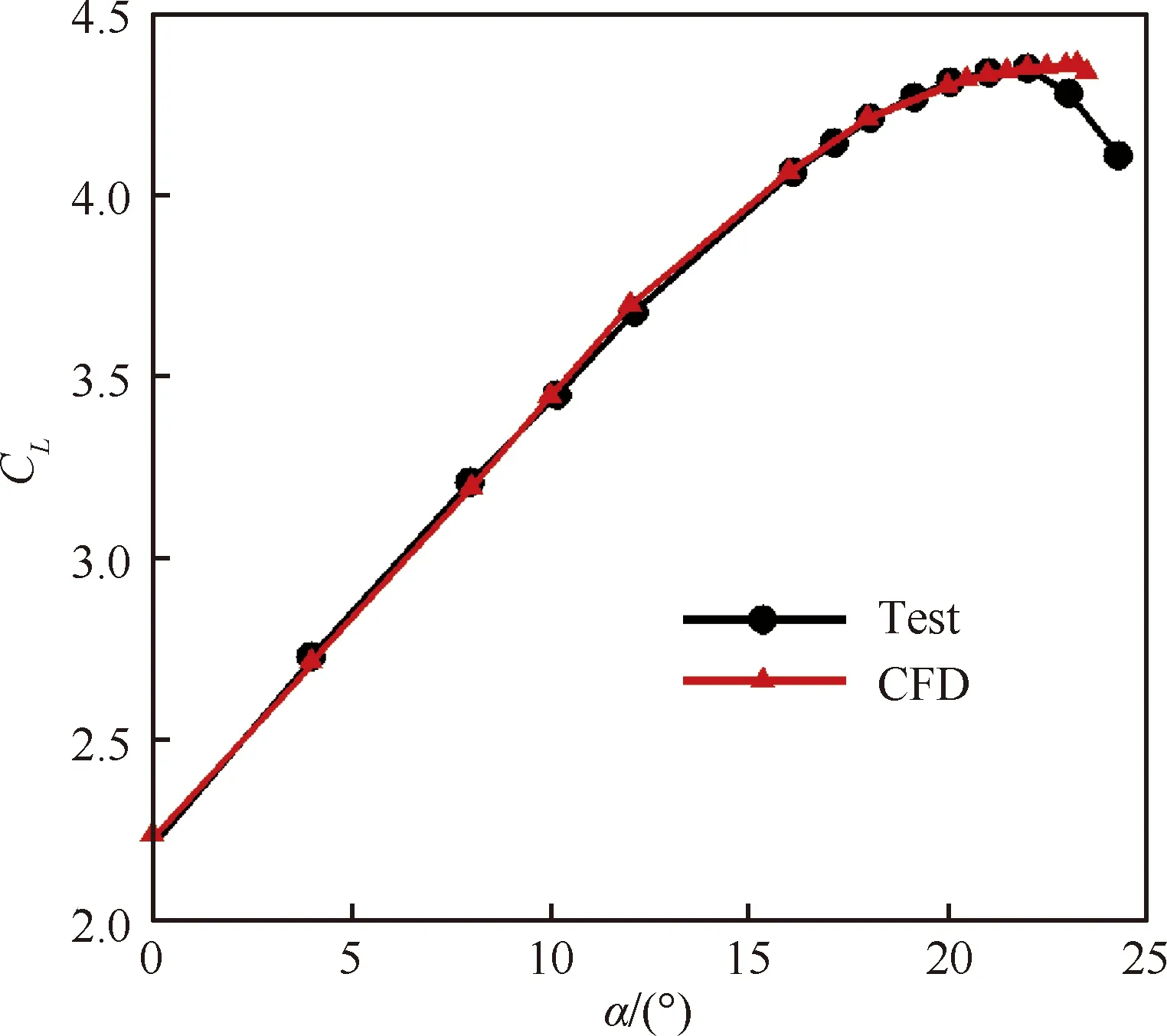
图2 30P30N翼型升力系数计算验证Fig.2 Numerical validation of lift coefficient for 30P30N airfoil

图3 30P30N翼型压力分布计算验证Fig.3 Numerical validation of pressure distribution for 30P30N airfoil
1.2 三维数值方法验证
为了验证本文数值模拟方法的可行性,选取NASA Trap Wing翼身组合体高升力构型的Config9构型[25],进行三维增升复杂构型的数值研究方法验证。在流场域内,采用多块结构网格策略生成贴体黏性结构网格,并对关键区域进行网格加密处理。表面及对称面计算网格示意如图4 所示,网格节点总数为900万。
计算条件为马赫数Ma=0.20、雷诺数Re=4.3×106。从图5和图6给出的气动特性曲线及压力分布可见,数值模拟与风洞试验结果吻合良好。各展向站位(η=0.17~0.85)的数值模拟与试验结果保持了较好的一致性,表明本文数值模拟方法较好地把握了各翼段的流动细节。本文采用的数值模拟方法满足复杂的三维增升装置流动问题研究需要。

图4 NASA Trap Wing网格拓扑及表面网格Fig.4 Mesh topology and surface grid for NASA Trap Wing
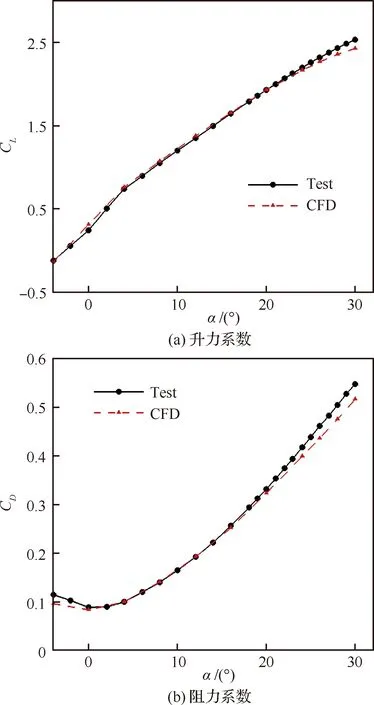
图5 NASA Trap Wing计算验证Fig.5 Numerical validation for NASA Trap Wing

图6 NASA Trap Wing不同展向站位的压力分布计算验证 (α=24°)Fig.6 Numerical validation of pressure distribution for different span locations of NASA Trap Wing (α=24°)
2 开缝克鲁格襟翼参数影响规律
前缘增升装置是延迟失速迎角,提供最大升力的主要部件。通过参数化方法描述开缝克鲁格前缘增升装置的几何形状与缝道配置,研究参数变化对流动特征与气动性能的影响规律是十分必要的。
2.1 克鲁格襟翼参数化方法
参数化方法是研究开缝刚性折叠钝头克鲁格流动形态与气动性能影响规律的前提。与前缘缝翼相比,克鲁格襟翼设计的细节变化多,为设计者提供了更多、更自由的选择。克鲁格襟翼头部半径基本不受基本翼型约束,设计范围大;对于给定的前梁位置,克鲁格襟翼的面积延伸量更大;此外,襟翼头部半径、襟翼头部与后部过渡位置的曲率、缝道参数等均对最大升力系数有很大的影响。因此,本文克鲁格襟翼的参数化方法遵循几何与运动机构特点,由几何参数与缝道配置参数两部分组成,如图7所示。
几何参数采用无量纲的定义方式,保证参数变化时几何外形的相似性,避免畸形克鲁格外形出现。刚性折叠钝头克鲁格襟翼由襟翼头部和后部构成,几何参数分别对两部分进行定义。克鲁格襟翼后段在襟翼收起状态下为巡航翼型的下表面,采用起始弦向位置Xstart、弦向长度L与厚度d这3个设计参数进行定义,经初步评估表明,襟翼后部厚度对气动性能的影响较小,因此本文中厚度为常值。采用样条曲线生成克鲁格襟翼头部形状,样条曲线控制点分别为克鲁格襟翼头部起点P1、襟翼头部前缘点P2、襟翼头部下表面最大厚度位置P3和襟翼头部终止点P4。控制点位置采用4个无量纲的几何参数进行描述:襟翼头部长度占后部弦向长度L的比例NL、襟翼头部宽度占长度的比例NH、P3在长度方向的相对位置NX、P2在高度方向的相对位置NY。通过CATIA,根据几何形状参数,在基础翼型上剖分出克鲁格襟翼后段,进而确定此方法可保证克鲁格襟翼折叠位置曲率的连续性。此外,本文简化克鲁格襟翼凹腔为方腔,凹腔深度与折叠后克鲁格襟翼头部最高点相切。
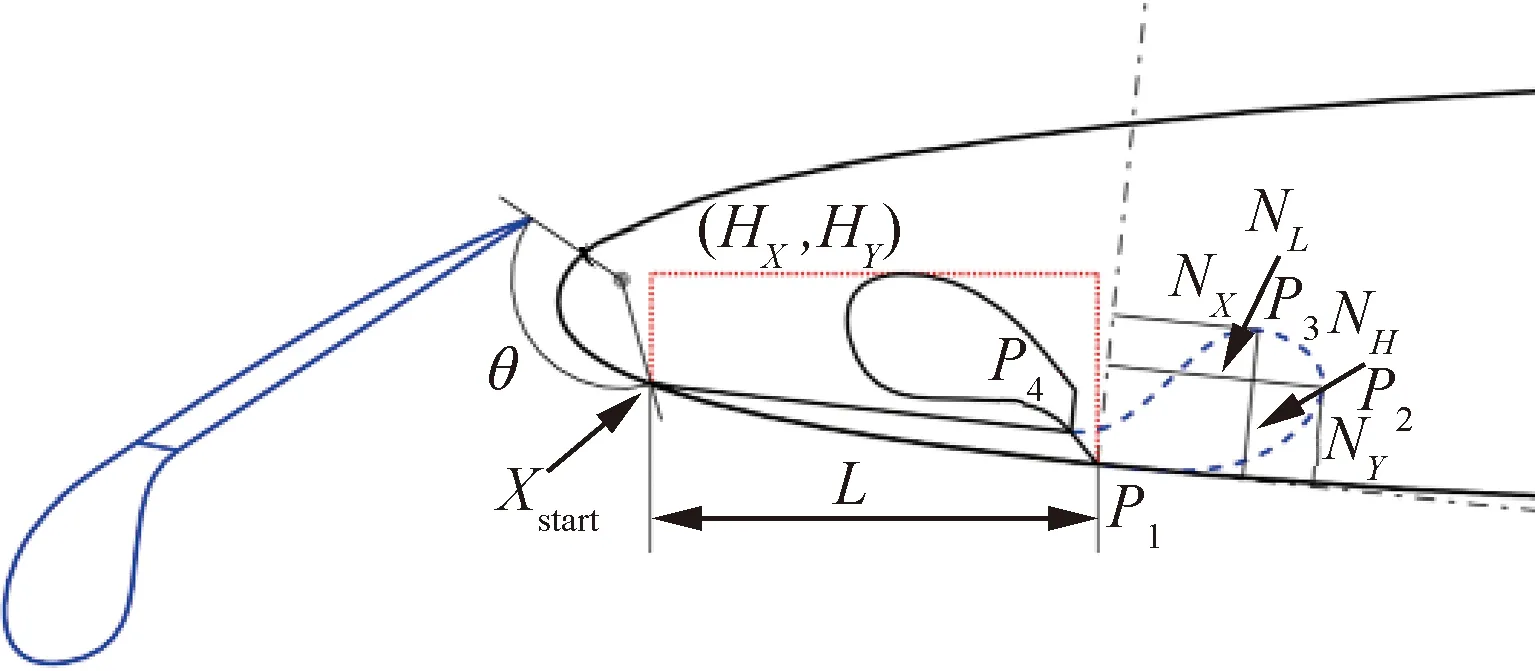
图7 开缝折叠钝头式克鲁格襟翼参数化方法Fig.7 Parameterization method of slotted folding bull-nose Krueger flap
与缝道宽度和重叠量对缝道配置定义的方式不同,本文选取铰链位置(HX,HY)与绕铰链偏转角度θ对克鲁格襟翼的缝道配置进行定义。此方法更加贴合克鲁格襟翼布置于下表面,并通过连杆机构,绕翼型前缘的铰链旋转至展开状态的运动特点,遵循了克鲁格襟翼缝道参数实际由铰链位置与偏转角度决定的特征;同时,易于实现铰链布置于翼型内部的约束,保证设计结果的工程可行性。
2.2 克鲁格襟翼参数影响规律
本节将围绕开缝刚性折叠钝头克鲁格襟翼的增升能力展开研究,分析克鲁格襟翼的流动特征,获得参数变化对最大升力与失速迎角的影响规律。
增升构型缝道参数对气动性能影响大,并且影响规律较为复杂。为了排除缝道参数带来的影响,得到克鲁格襟翼几何参数以及偏转角度的影响规律,本节研究中缝道宽度和重叠量与30P30N标模一致,缝道配置最终在优化设计中解决。此外,放宽工程应用中的几何约束,采用控制变量法,研究单一设计参数在较大范围变化时对增升能力的影响。
以30P30N巡航翼型为基础,参考Wild等研究结果[19],得到克鲁格襟翼初始几何外形。克鲁格襟翼参数规律影响研究的参数范围如表1所示。计算状态为马赫数Ma=0.2,基于平均气动弦长的雷诺数Re=9.0×106,计算网格如图8所示。
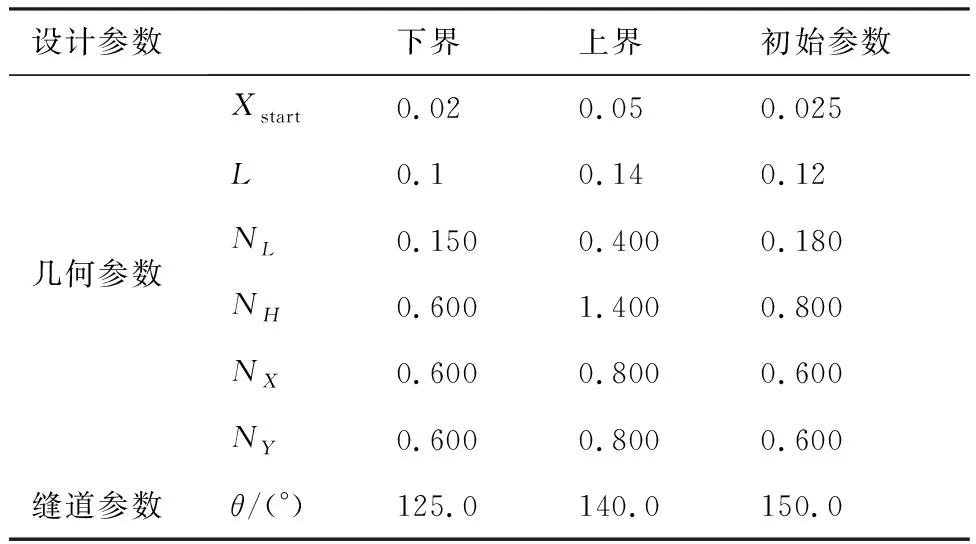
表1 克鲁格襟翼参数影响研究的参数空间

图8 开缝钝头克鲁格襟翼计算网格Fig.8 Computational grid for slotted bull-nose Krueger flap
2.2.1 几何参数影响规律
通过数值分析可知,开缝刚性折叠钝头克鲁格襟翼对几何外形变化十分敏感。图9分别给出了各几何参数的几何形状变化以及失速特性。Xstart确定了克鲁格襟翼上表面后缘的曲率,如图9(a) 所示,量值越小,越靠近前缘曲率越大,上表面需要克服的逆压梯度越大,越容易引起上表面流动分离。因此,克鲁格襟翼应起始于曲率变化相对和缓的区域,避开前缘。其中,克鲁格襟翼后部长度L与头部长度比值NL直接影响弦长的延伸量,如图9(b)、图9(c)所示。由于本文参数定义的无量纲方式,克鲁格襟翼长度越大,前缘半径越大,可避免襟翼头部加速过快导致流动分离。两参数对增升能力的影响最大。
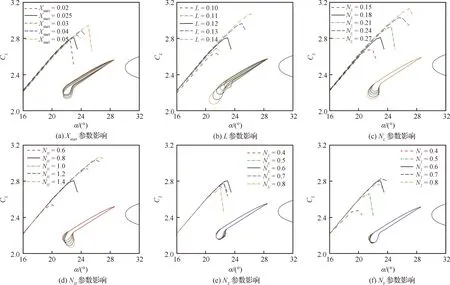
图9 开缝钝头克鲁格襟翼几何参数对失速特性影响Fig.9 Impact of each geometry parameter on stall behavior for slotted bull-nose Krueger flap
克鲁格襟翼头部宽度占长度的比例NH,能够显著改变襟翼前缘半径,使参数化方法能描述半径较小的“直杆式”简单克鲁格襟翼与半径较大的“D形”钝头克鲁格襟翼,如图9(d)所示。计算结果反映出增升装置期望较大的前缘半径。NX、NY能够影响克鲁格襟翼头部的曲率分布,NX主要改变下表面凹角区域,NY主要影响上表面,如图9(e)、图9(f)所示。通过几何形状的局部变化,影响克鲁格襟翼增升效果,其影响规律非单调,存在最佳数值。相较而言,NY对克鲁格襟翼增升效果影响更加明显。
2.2.2 偏转角度影响规律
克鲁格襟翼偏度对增升能力影响最大,本文对襟翼偏度范围125°~150°开展研究。图10给出了开缝克鲁格襟翼偏角对失速特性影响。由图可知,随着偏度由小到大,克鲁格襟翼的增升效果先增强后减弱。相对于前缘缝翼,克鲁格襟翼倾向于“低头”的偏转角度。
为了得到克鲁格襟翼偏度影响的流动机理,选取增升最佳构型(θ=130°)以及两个偏角(θ=125°,θ=135°),并分析迎角α=26°下的流态与压力分布。从图11中的流态分析可知,迎角α=26°时,偏度较小的两构型失速形态为主翼后缘分离发展引起后缘失速,θ=125°构型已失速,θ=130°构型仍处于后缘流动分离继续发展状态。而大偏度θ=135°构型处于前缘失速状态,其克鲁格襟翼由于强逆压梯度,分离泡即将破裂,引起克鲁格襟翼上表面分离。

图10 开缝钝头克鲁格襟翼偏角对失速特性的影响Fig.10 Impact of deflect angle on stall behavior for slotted bull-nose Krueger flap
图12的压力分布表明,偏转角度影响克鲁格襟翼自身吸力峰值和对主翼负压峰值的控制作用,偏度过大引起主翼前缘流速较高,逆压梯度大,容易引起克鲁格自身上表面流动分离;偏度太小对主翼流动控制能力不足。因此,开缝克鲁格襟翼偏转角度需要综合考虑实现稳定的后缘失速形态与较强主翼流动控制能力这两个设计目标,达到最佳增升效果,偏转角度是克鲁格襟翼设计的核心参数之一。

图11 α=26°时不同偏角下克鲁格襟翼流动形态Fig.11 Flow behaviors for Krueger flap with different deflect angles at α=26°
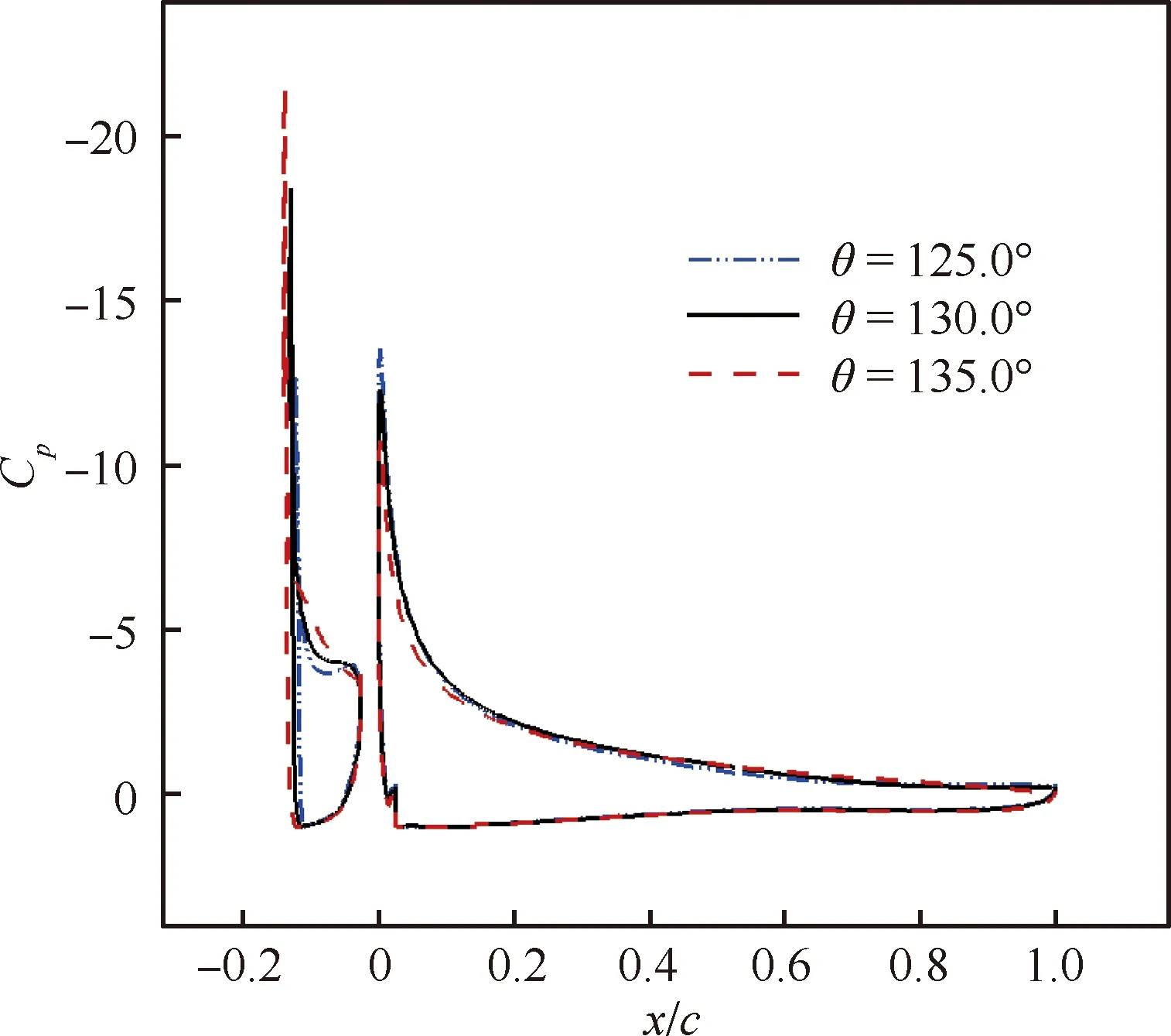
图12 α=26°时不同偏角下克鲁格襟翼压力系数分布Fig.12 Pressure coefficients distribution for Krueger flap with different deflect angles at α=26°
2.2.3 设计原则
基于上述研究结果和工程应用,克鲁格襟翼设计原则如下:
1) 克鲁格襟翼后部设计,襟翼起始位置Xstart应绕过翼型前缘,起始于下表面曲率变化相对和缓的区域。翼身融合布局,还应规避截面翼型前加载区域,以避免曲率变化引起克鲁格襟翼上表面分离。后部长度L越大越好。但两参数需要考虑前梁位置限制。根据参数影响规律,本文选取Xstart=0.025、L=0.12,以保证机翼前梁x/c=0.15的位置约束。
2) 克鲁格襟翼头部形状由NL、NH、NX、NY这4个参数综合确定。参数影响规律表明,襟翼头部长度比例NL与宽度占长度的比例NH对襟翼前缘半径有决定性影响,长度宽度较大的头部增升效果好,但仍需满足克鲁格襟翼及运作机构能够完全收入机翼前端的设计需求。NX、NY能够改变克鲁格襟翼头部的曲率分布,NX=0.6、NY=0.7附近能够得到最佳效果。
3) 克鲁格襟翼偏转角度影响增升效果与失速形态,是克鲁格襟翼设计的核心参数之一。最佳偏角的选取,需要结合铰链位置等缝道参数开展深入的优化设计。
结合工程可行性,克鲁格襟翼设计需要考虑以下设计约束:增升装置收起时保证高速巡航构型,克鲁格襟翼及运作机构能够完全收入机翼前端,不影响前梁布置,旋转铰链位于翼型前缘内部的空间限制。为了实现对机翼前缘虫尘沾染的遮蔽效果,增升状态下克鲁格襟翼后缘需位于翼型上表面遮蔽线上方[26]。
3 开缝克鲁格襟翼优化设计
基于克鲁格襟翼设计原则,加入铰链位置作为设计变量,实现几何参数和全部缝道参数的优化设计。开缝克鲁格优化设计原则为:在满足几何外形、运动机构以及气动设计要求等多学科约束下,以提高最大升力和延迟失速迎角为设计目标,开展克鲁格襟翼几何参数与缝道参数的最佳配置的优化设计。
3.1 优化设计方法
本文构建的克鲁格襟翼优化设计框架如图13 所示。优化设计模块中,首先根据设计变量通过CATIA脚本进行克鲁格襟翼外形生成,并进行增升构型配置,然后自动生成网格并对不同设计点进行数值模拟与分析,判断克鲁格襟翼是否符合各约束限制的要求。基于项目组前期研究基础[27],优化设计流程将Kriging[28]代理模型与遗传算法结合,并采用松散式代理模型管理框架,以保证代理模型模拟精度的同时,大幅度提高优化效率。采用多目标综合优化设计方式,以改善大迎角气动性能同时保证中等迎角气动效率,获得了较好的综合增升效能。
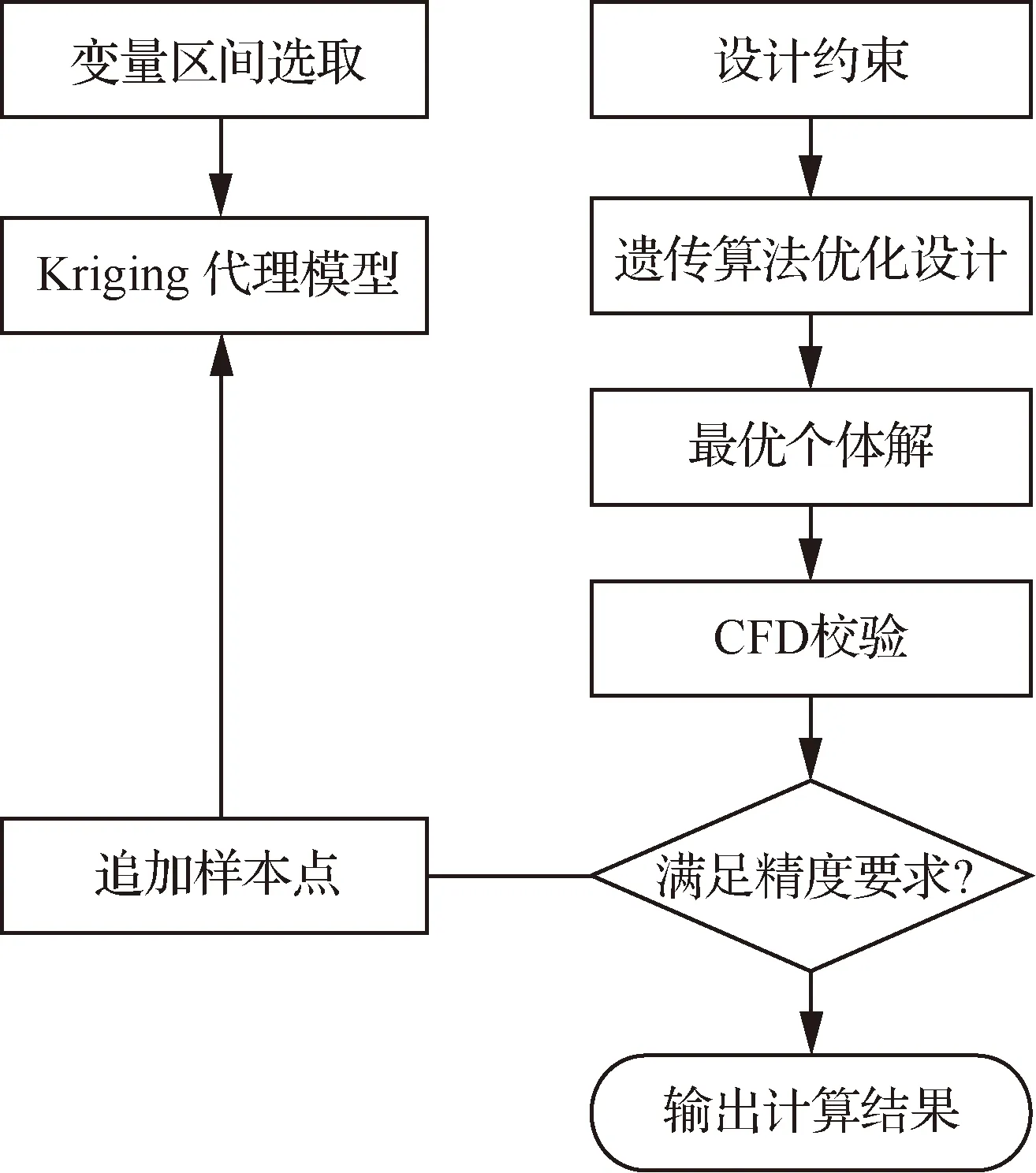
图13 优化设计流程Fig.13 Optimization design process
3.2 优化设计目标与约束
虽然代理模型具有较强的非线性映射能力,但其预测精度受到非线性强弱的影响,而增升装置参数间的影响十分复杂,且优化设计对精度要求较高,为提高代理模型的预测精度,保障优化设计结果。根据设计原则,优化设计参数范围选取如表2所示。其中,在参数影响规律研究基础上,增加铰链位置参数,其参数范围保证了旋转铰链位于翼型前缘内部。优化设计参数空间表明,克鲁格襟翼头部几何参数与缝道配置是影响增升效果的主要参数;开缝克鲁格襟翼优化设计实质是对克鲁格头部几何外形与缝道配置的匹配设计。
前缘增升装置均以提升最大升力系数和失速迎角为设计目标。然而,DLR增升装置设计研究表明[29],直接采用最大升力系数作为优化设计目标将显著提高优化设计的时间耗费,采用大迎角气动特性进行优化设计并对失速特性进行后验分析更实用。为了保证中等迎角气动效率,本文以α=12°与α=22°两个状态的升力系数作为优化目标,并在优化过程中对每代最优设计的失速特性进行后验分析。

表2 优化设计参数范围Table 2 Parameter design space for optimization
为了提高优化设计结果的工程可行性,进一步对气动系数、压力分布与几何形状施加约束。结合BWB布局低速配平的设计难点,对力矩进行限制,避免低头力矩过大。参考缝翼的设计经验,前缘增升装置的缝道应使主翼上表面较早形成汇流边界层,以降低主翼头部吸力峰值;同时,应避免前缘增升装置自身因流速过高引起激波诱导的流动分离现象。因此,限制克鲁格襟翼吸力峰值不低于-15.5。几何形状上,通过后验方式,在完成克鲁格襟翼剖分与增升构型配置后,对以下3点设计约束进行校验:襟翼能收入主翼前缘,最高点低于主翼局部厚度的60%;襟翼展开过程中与主翼无碰撞;增升状态下满足虫尘沾染的遮蔽效应要求。
优化设计目标和约束条件表示为
1) 优化目标
min -(CL,dp1+CL,dp2)
(1)
2) 设计约束
气动约束:
(2)
压力分布约束:
(3)
式中:Cpmin为克鲁格襟翼压力峰值,下标dp1表示α=12°,dp2表示α=22°。
3.3 优化设计结果
构建Kriging代理模型:初始训练样本为100个,测试样本为30个。遗传优化每代群体个数为200,杂交概率为0.8,变异概率为0.05,进化60代。优化过程中目标函数的收敛曲线如图14 所示。如表3所示,本文采用的代理模型的预测结果可靠,满足优化设计需求。
克鲁格襟翼初始设计与优化设计结果几何外形如图15所示。优化结果头部长度增加,前缘半径增大,缝道更加狭小,襟翼后缘与主翼上表面切线方向一致。对优化设计结果开展综合评估,通过优化结果气动力系数前后比较可知:优化结果的升力线斜率更大,失速迎角αstall由23.5°提升至30°,最大升力系数达到3.4。与30P30N缝翼设计相比,最大升力系数提高29%,失速迎角提高3.5°,并且克鲁格襟翼阻力更小,低头力矩量较小,符合BWB布局设计需求,如图16所示。
进一步对优化设计结果开展流态与增升机理分析。流态分析表明优化构型流动稳定,后缘失速形式失速特性良好,如图17所示。通过优化前后的压力分布比较发现,前缘增升装置施加负压峰值约束可以有效降低设计结果的吸力峰值,避免了开缝克鲁格襟翼前缘出现声速区诱导流动分离。与缝翼相比,克鲁格襟翼的面积延伸量更大,克鲁格襟翼升力贡献高,并且优化设计结果环量转移效果明显,通过控制主翼吸力峰值延迟了失速迎角,如图18所示。
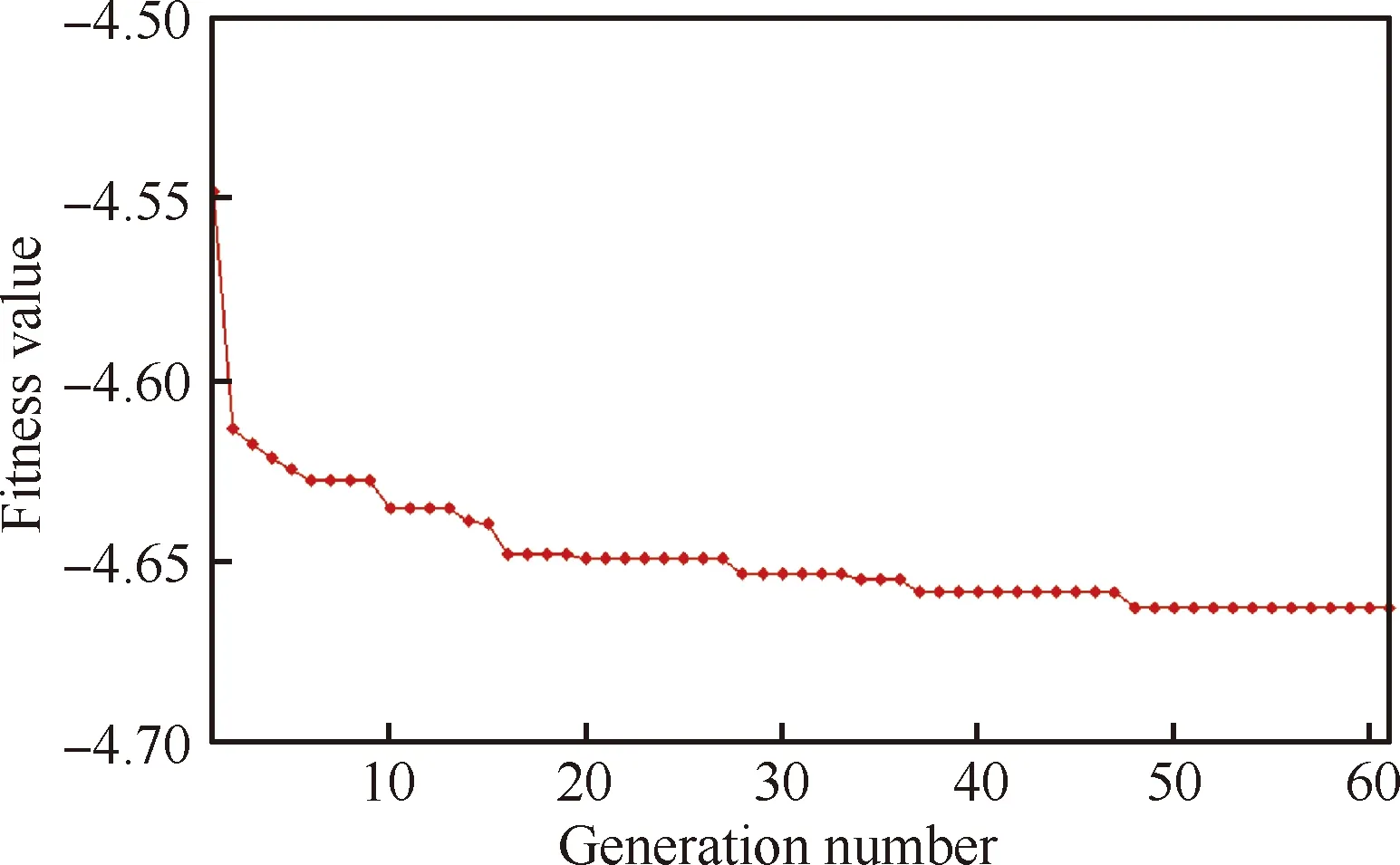
图14 优化设计目标函数收敛曲线Fig.14 Coverage history of optimization design objective function
表3 克鲁格襟翼代理模型精度校验
Table 3 Calibration of surrogate model for Krueger flap

图15 克鲁格襟翼优化前后与经典缝翼几何形状比较Fig.15 Geometry comparison of Krueger flap before and after optimization with a typical slat

图16 克鲁格襟翼优化前后与经典缝翼气动特性比较Fig.16 Aerodynamic characteristic comparison of Krueger flap before and after optimization with a typical slat
优化设计结果增升性能的提升是几何参数与缝道参数综合设计的结果。襟翼头部前缘半径与弦长加大,降低襟翼上表面流速,实现了前缘增升装置的压力恢复,避免上表面流动分离现象,流动更加稳定。优化后的缝道配置上,偏角基本实现襟翼尾迹指向方向与主翼上表面相切,使缝道射流平滑流过主翼前缘;优化结果缝道宽度降低,对主翼流动控制能力增强,使得主翼尾迹与缝道射流交混作用加强,主翼尾迹流趋于稳定,而主翼前缘吸力峰降低也降低了逆压梯度,有利于保持尾迹稳定。
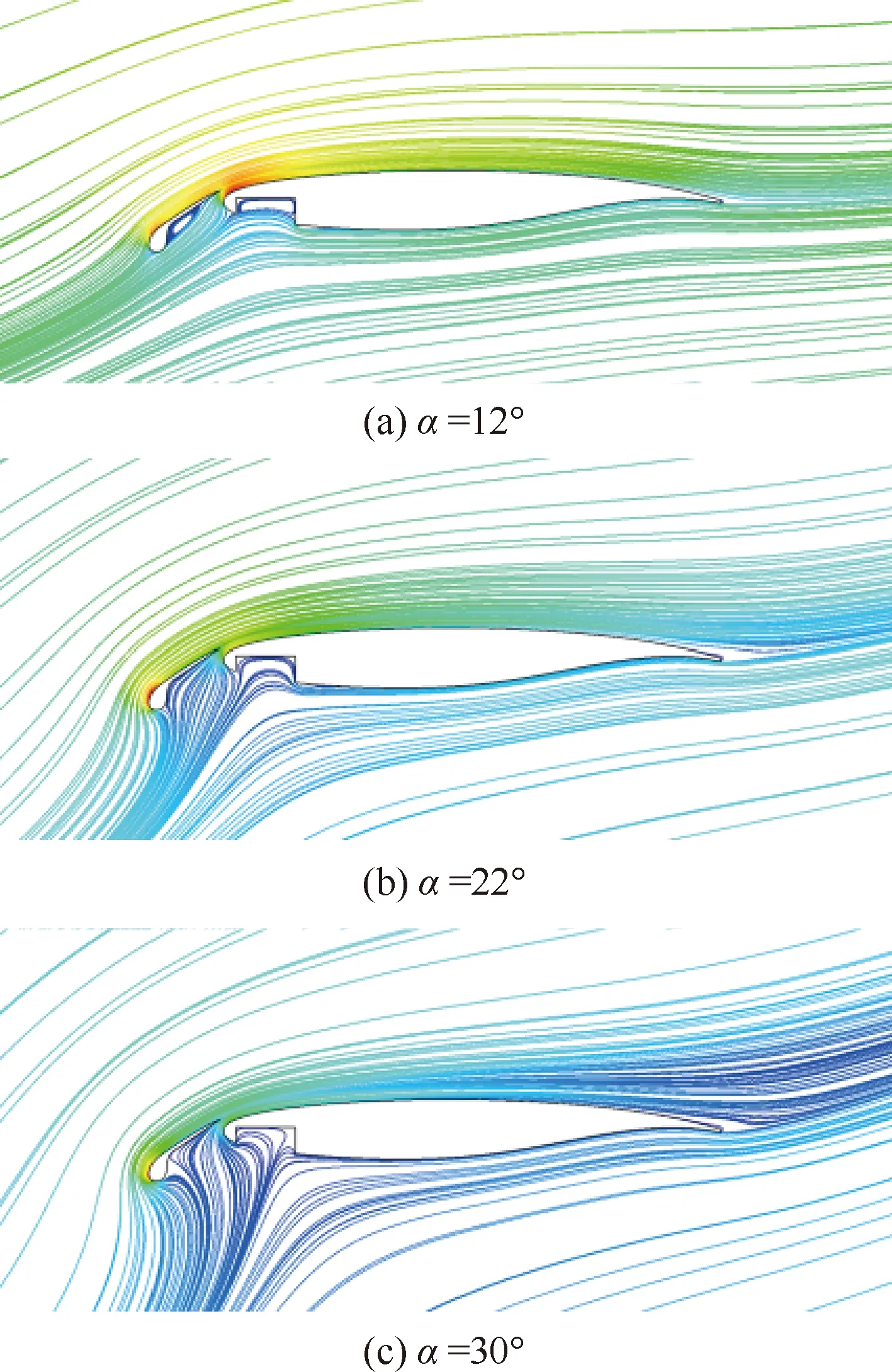
图17 优化设计结果的流动形态Fig.17 Flow behaviors for optimization design result
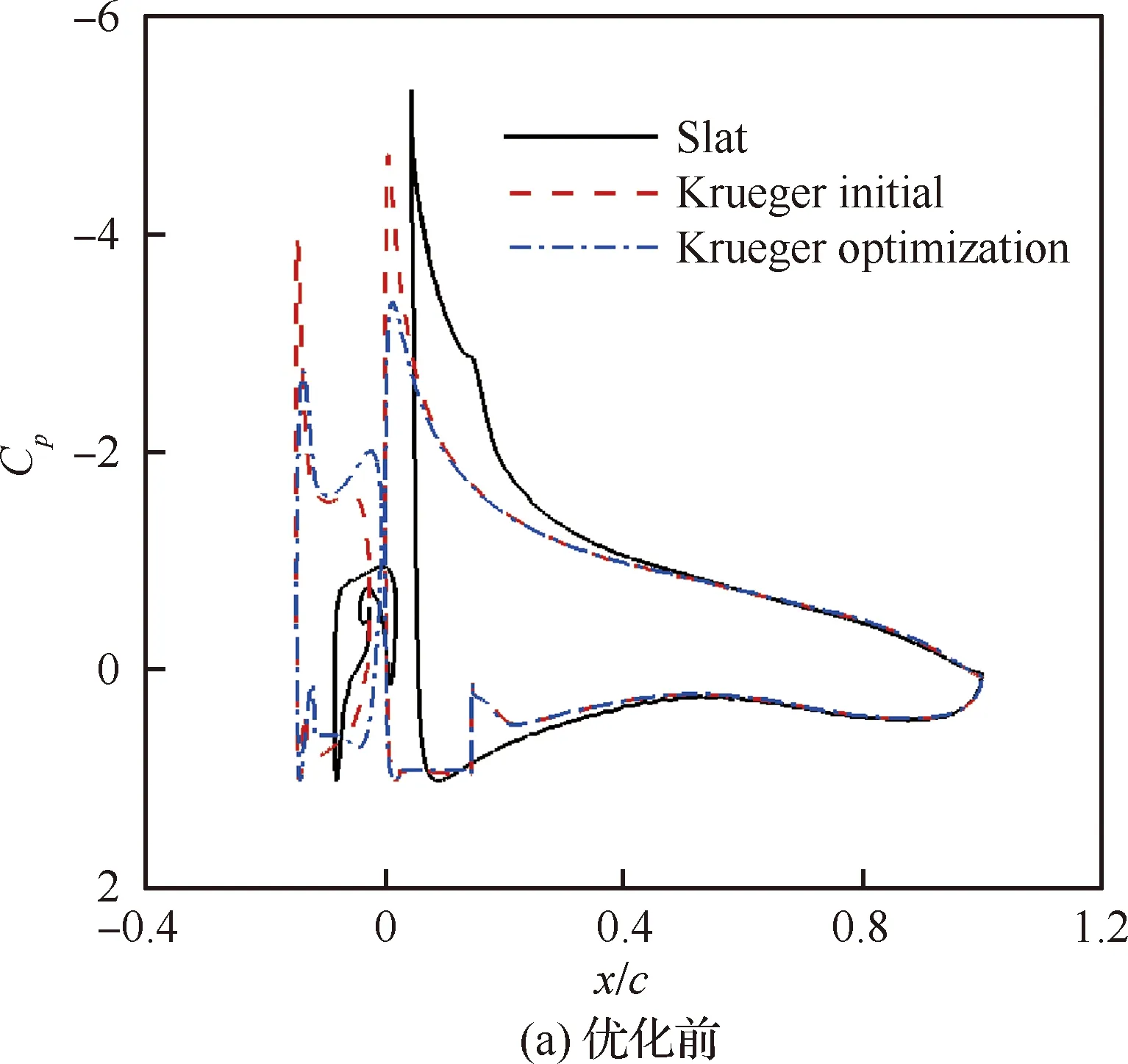
图18 优化前后压力分布比较Fig.18 Comparison of pressure distribution before and after optimization
图19表明,克鲁格襟翼优化设计结果满足工程实际设计约束。铰链位置位于翼型前端上部,襟翼收起状态符合空间限制要求,增升状态满足遮蔽效应要求。
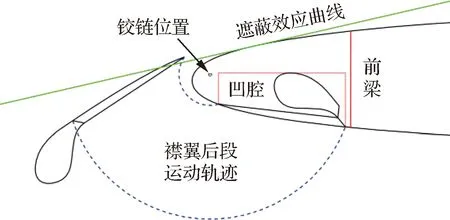
图19 优化结果空间设计约束检查Fig.19 Space design constraints examination for optimization result
4 翼身融合布局开缝克鲁格襟翼
基于二维克鲁格参数规律与优化设计研究方法,针对NPU-300-II的BWB概念设计方案,进行开缝克鲁格襟翼设计,并采用数值模拟对增升能力进行评估。最终,通过风洞试验方法验证了以前缘开缝克鲁格襟翼和后缘简单襟翼作为翼身融合布局增升构型的气动特性。
4.1 数值模拟
沿用第3节开缝克鲁格襟翼的优化设计方法,以BWB布局NPU-300-II方案外翼后缘转折点翼型(图中黑色实线)为基础,进行二维克鲁格襟翼的优化设计,对机翼各截面控制翼型采用优化后的克鲁格襟翼参数配置,建立了三维克鲁格襟翼数模。NPU-300-II的BWB概念设计方案的增升构型如图20所示。图中蓝色部分对应前缘开缝克鲁格襟翼,红色部分为偏转后的后缘简单襟翼。各控制截面的克鲁格襟翼与简单后缘襟翼控制线用红色实线表示。
采用数值方法分析开缝克鲁格襟翼的流动现象,评估三维克鲁格襟翼推迟失速的能力。计算状态为Ma=0.2,海平面标准大气状态。干净构型与克鲁格襟翼展开构型的气动特性如图21所示。由图可知,开缝前缘克鲁格襟翼具有良好的增升能力,显著延迟失速,附加低头力矩较小。开缝克鲁格襟翼展开前后构型的流态比较,如图22所示。干净构型在α=15°已失速,机翼上表面流动完全分离;开缝克鲁格襟翼展开后,主翼上表面为附着流动,体现出良好的流动控制能力。随着迎角增大,α=19°时,外翼后缘出现流动分离,至α=23°时,外翼后缘流动分离与翼梢涡结合,引起翼梢流动分离并向内发展。
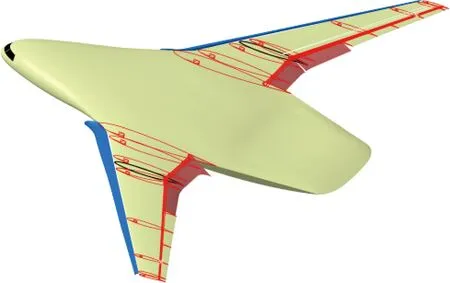
图20 BWB增升构型与前后缘增升装置控制型线Fig.20 BWB high-lift configuration with control line for leading and trailing edge high-lift devices
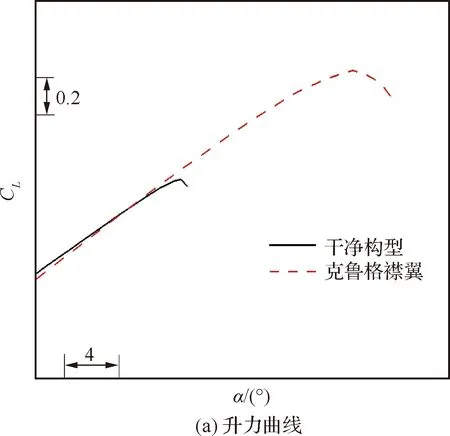

图21 BWB布局克鲁格襟翼展开前后气动特性比较Fig.21 Comparison of aerodynamic characteristics for BWB configuration with folded and deployed Krueger flaps
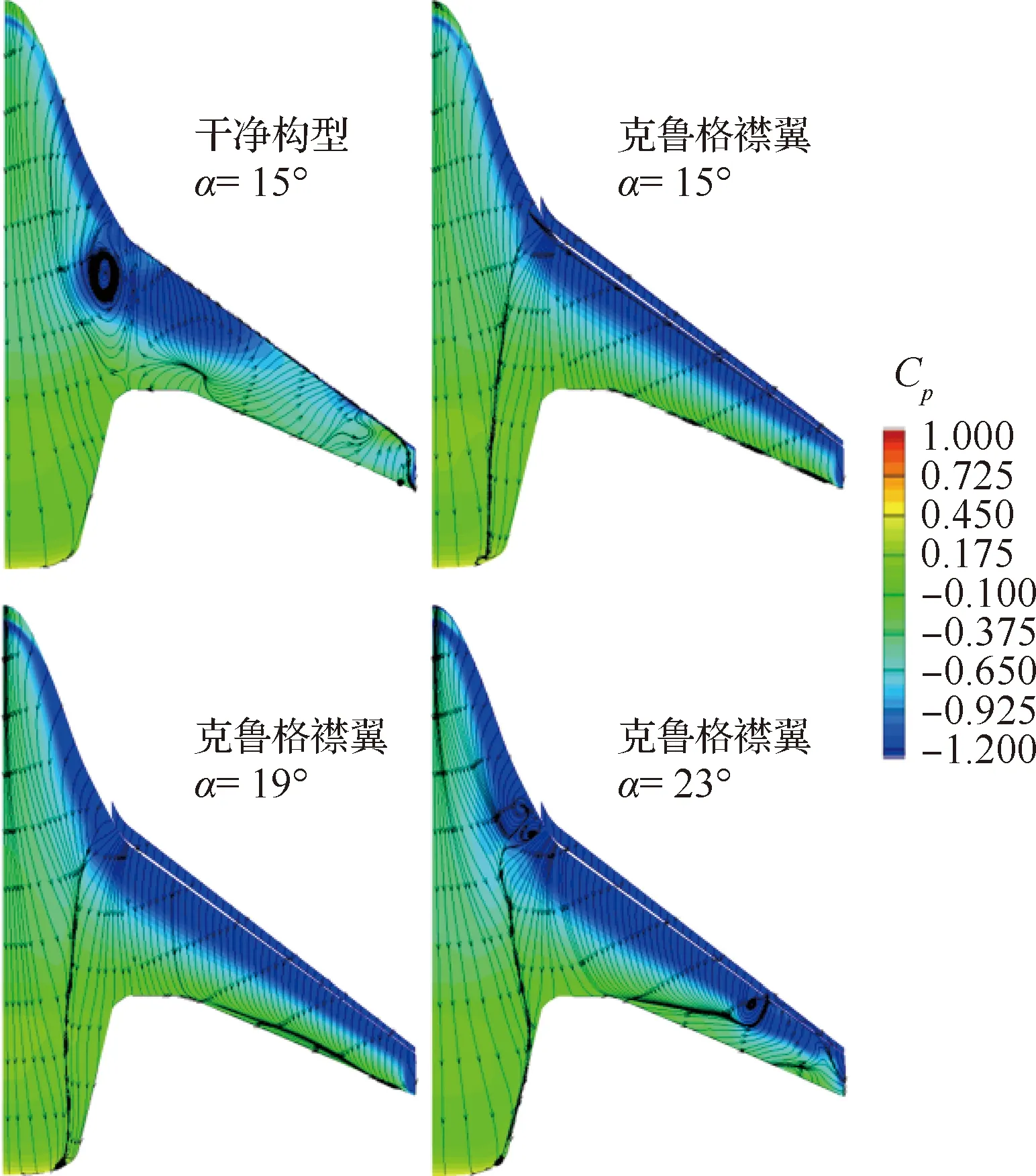
图22 BWB布局前缘克鲁格襟翼装置展开前后流态比较Fig.22 Comparison of flow behaviors for BWB configuration with folded and deployed Krueger flaps
数值模拟结果表明开缝克鲁格襟翼能够有效控制主翼流动,显著提升BWB布局的低速增升能力。虽然大迎角状态下,流动分离由外翼后缘出现,逐步由翼梢向内侧发展的控制效果并不理想;但后期针对机翼各截面控制翼型开展细致设计,可以改善或消除此现象,进一步提高低速气动性能。
4.2 风洞试验
为了进一步确认BWB布局低速增升构型的气动性能,在中国航空工业空气动力研究院FL-51进行了模型缩比1∶22的低速风洞试验。该风洞为低速直流式风洞,试验段尺寸宽×高=4.5 m×3.5 m,试验风速为70 m/s,试验Re=5.5×106。进行了基本构型、起飞构型和着陆构型等测力与流动显示试验,增升装置采用前缘克鲁格与后缘简单襟翼,如图23所示。
图24给出低速干净构型、起飞与着陆3种构型的试验结果。3种构型均具有良好的失速与俯仰力矩特性,采用前缘克鲁格襟翼与后缘简单襟翼组合的增升装置,能够满足起降升力要求,低头力矩增量在纵向控制舵面可控制范围内。

图23 低速风洞试验概念方案Fig.23 Conceptual scheme in low speed wind tunnel test

图24 概念方案低速风洞试验结果Fig.24 Results for conceptual scheme low speed wind tunnel test
5 结 论
1) 克鲁格襟翼是翼身融合布局前缘增升装置的理想选择,针对BWB布局开缝折叠钝头克鲁格襟翼设计问题,建立符合其外形与传动机构特点的参数化方法,可以准确描述几何外形与缝道配置,工程实用性强。
2) 通过克鲁格襟翼参数影响规律研究以及对流动形态和增升机理的分析,表明开缝克鲁格襟翼增升效果对设计参数较为敏感,结合工程设计约束,提出开缝克鲁格襟翼设计原则。
3) 通过对克鲁格襟翼头部形状和缝道配置开展优化设计研究,优化设计结果满足各项约束要求,失速迎角与最大升力系数明显提高。
4) 针对BWB布局,建立前缘克鲁格襟翼与后缘简单襟翼的增升构型。三维初步应用表明,可显著提高BWB布局增升构型的气动性能,可应用于翼身融合类民机布局研究,并可为其他用途翼身融合类飞机设计提供参考。
