数学高考解题能力培养策略分析

贾 宽

(内蒙古乌兰察布市北京八中乌兰察布分校 012000)

波利亚曾说过：“掌握数学意味着什么？意味着善于解题.”数学学习离不开解题，所有的数学学习，归根结底就反映在学生的解题能力上.尤其是在高考中，学生的数学解题能力直接决定了学生的数学成绩.因此，教师在具体的高中数学教学中，必须要结合高考数学的要求，借助数形结合思想，以提升学生的解题能力.

一、数形结合思想在集合考题中的应用

集合这一部分的知识是高中数学学习的重点，同时也是高考的重点.在以往的高考中，一部分学生在解题的过程中，常常出现一定的问题，进而导致解题效果不佳，在一定程度上影响了高考数学的得分.而在数形结合思想模式下，教师可指导学生在解答该类题目的过程中，可采用数形结合的思想，将题目中的数量进行转化，使其成为对应的图形，进而提高该类题目的解答效果.

例如，在高中数学中，集合与函数概念是最为常见的考点之一.在具体培养学生解题能力的过程中，就可以借助数形结合的思想进行.具体来说，教师在对这一部分解题能力进行训练的过程中，可采取例题：三年级1班中有42人，18人选择了微机小组，15人选择了象棋小组，还有12人两个小组都没有参加，问两个小组都参加了一共有多少人.针对这一问题，教师在培养学生解题能力的过程中，就可以利用数形结合的方式，引导学生先画一个大圈，并在外面标上42.其次，在这一大圈内画上两个具有重合的小圈，分别标上18、15，而在大圈之内的小圈外则写上12.在这种情况下，通过图形的应用，题目中的数量关系一目了然，进而使得学生对问题进行有效的解答.

二、数形结合思想在函数题目解题中的应用

函数是高中数学的学习中的重难点，同时也是高考中数学考查的重点所在.由于函数所涉及到的知识具有较强的理论性，且涉及范围比较广，以至于学生在解答该类题目的过程中，频频出现错误等.尤其是针对一些难度较大的函数求知问题来说，在对其进行解答的过程中，单纯地采用代数方式，很难对其进行正确的解答，而通过数形结合思想的应用，可将其中复杂的代数关系进行转化，使其生动形象地呈现在面前，进而结合图形，对函数中的问题进行定量分析，进而有效提升了高考数学的解题效率.

图1

例如，已知x、y满足x2+y2-4x=0，求(x+1)2+(y+1)2的最值.在解答该问题的时候，单纯地采用数学知识进行解答，不仅难以顺利解答，还会在一定程度上加大解答的难度，进而使得学生在解题的过程中，浪费了大量的时间，对高考数学考试产生了严重的影响.而在数形结合思想的应用下，学生在对该问题进行解答的过程中，可将其进行转化为图形(如图1所示)，并在此基础上，结合图形和相关数学知识，对其进行正确的解答.

需要说明的是，学生在利用数学结合思想解答函数问题的过程中，部分学生对于两点间的距离、导数等相关概念掌握不够充分，以至于限制了数形结合思想的应用.这就要求教师在提升学生利用数形结合思想解题能力的过程中，必须要对该部分内容进行重点讲解，以确保学生数形结合思想的顺利应用.

三、数形结合思想在不等式解答中的应用

在数学高考中，不等式占据重要的部分.以往学生在对其进行解答的过程中，常常单纯地采用代数的方式，对其进行解答.而这种解答模式下，很难取得良好的效果，甚至还会导致学生在解答的过程中，走进死胡同中.基于此，教师可引导学生借助数形结合的思想，将问题转化为函数图象，进而使得问题迎刃而解.

图1

例如，当a为何值时，方程2a2x2+2ax+1-a2=0的两个根在(-1,1)之间？在对其进行解答的过程中，教师可引导学生结合已知方程式，将y=2a2x2+2ax+1-a2函数的图象画出(如图2)，进而在此基础上，指导学生结合函数图象，对其进行观察，并结合一定的数学知识，求出正确的值.

四、数形结合思想在解析几何题目中的应用

解析几何题目历来是高考的重难点，但是学生在对其进行解答的过程中，也面临着较大的难度.基于此，教师在引导学生对其进行解答的过程中，可以充分利用数形结合的思想，将其转化为图形，对其进行解答.具体来说，利用数形结合思想在对其进行解答的过程中，应首先建立平面直角坐标系，并将题目中的几何条件进行转化，使其成为代数条件；最后，根据题目中的代数条件，进行运算求解.

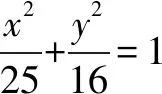
图3

在对解析几何进行解答的过程中，尤其是针对距离、斜率、倾斜角等解析几何问题进行解答的过程中，即可充分利用数形结合思想，对其进行简化处理，进而对其进行有效的解答.

数形结合不仅是一种数学思想，更是一种数学解题能力，将其应用到高考数学知识的解答过程中，不仅对试题进行了简化处理，进一步提升了数学试题的解答效率.因此，教师在具体培养学生高考数学解题能力的过程中，应加强数形结合思想的研究，并充分借助这一方式，提升学生的解题能力.