高速铁路环境下基于RSSI的距离估计算法优化

(中国铁道科学研究院，北京 100081)

随着无线传感器技术的发展，以定位为基础的服务得到了广泛的应用[1]。它被广泛应用于军事国防、环境监测、抢险救灾、医疗卫生和工农业控制等重要领域[2]。在我国由于地形和地质环境的特殊性，崩塌、滑坡等地质灾害较为严重[3]。其中，铁路是遭受崩塌、滑坡危害最频繁、最严重的一项工程。滑坡破坏了线路、中断行车、危害站场，毁坏铁路桥梁及其它设施，摧毁隧道，甚至会造成车翻人亡的行车事故[4]。为了降低滑坡对列车和人员的伤亡，需要对铁路沿线的山体进行监测，及时掌握滑坡的发生，并将滑坡发生的信息传递给临站的列车以进行相应的操作。因此，获得提高无线传感器节点的定位精度成为了研究的热点[5]。 在山体滑坡的室外定位中，常用的硬件设施是GPS[6]，需要将带有GPS模块的传感器部署在山体上，当上位机接收到GPS的位置信息发生变化时，认为该地区发生了滑坡事件，并将该信息发送给列车做出相应的调整。然而，使用较为廉价的GPS模块可以降低监测设备的成本，但其定位精度较低，为了改进这一缺陷，使用无线传感器节点代替GPS节点进行滑坡位置的确定。而在滑坡监测中，可以通过传感器节点距离的变化来判断滑坡的发生。

通常测距的方法有RSSI[7]、TOA[8]、AOA[9]等。其中TOA方法测距精度较高，但是对硬件要求高。AOA方法比RSSI方法测距精度高，但该方法需要额外硬件支持，硬件体积较大[10]。RSSI方法对硬件要求较低，不需要额外硬件的支持，操作简便。因此，本文采用RSSI方法来判断节点发生的情况。但是通过RSSI利用LNSM方法得到的距离偏离真实距离较远，误差较大[11]，需要对该方法进行改进以获得较高精度的距离，减小距离误差。在文献[12]中，通过分析RSSI与距离d的数据模型关系，得到了RSSI与d的Log数据模型，将该模型进行修正，使其误差尽量最小。并使用AP训练得到Log模型中的未知参数，最后通过RSSI来定位未知节点坐标。文献[13]提出了一种三边-加权质心定位算法，该算法首先确定定位三角形，然后以测试距离的影响大小作为权值来计算节点的估计值，此方法可以减小定位的面积。在文献[14]中，主要针对三角形质心定位算法误差大的缺陷，提出了改进的算法—CLIP算法，仿真实验表明，改进算法能提高无线传感器节点的定位精度。本文主要以提高部署在高铁沿线山体上的无线传感器节点移动的精度作为目的，应用加权和回归算法改进传统LNSM测距方法，得到较高估计精度的距离。

1 LNSM算法

根据采样得到的节点之间信号强度值RSSI，利用LNSM方法，可以获得两个节点之间的估计距离。

在LNSM方法中，为了减小RSSI波动带来的影响，对RSSI采用均值的方法作为某个位置处的信号强度值。然后根据RSSI与已知的距离计算LNSM中的路径损耗指数n和其它的参数

(1)

式中，m表示所有计算得到的路径损耗指数n的个数；RSSIi+1和RSSIi分别表示第(i+1)和i个位置处收发节点之间的信号强度值；di+1和di表示收发节点之间第(i+1)和i个位置之间的距离；n表示该特定环境下的路径损耗指数。

RSSIi=Pt-PL(d0)-10nlgdi=Ai-10nlgdi

(2)

式中，Ai=Pt-PL(d0)；Pt表示传感器的发射功率；PL(d0)表示在参考距离处的路径损耗，通常参考距离取1 m。

在传统的LNSM方法中，为了减小参数A的偏差，一般采用取均值的方法，即

(3)

式中，s表示计算得到参数A的个数；Ar表示所有值的均值。从而节点之间的距离

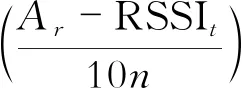
(4)

式中，RSSIt表示待测位置处的信号强度值；dt表示根据公式得到的节点间的距离。

2 改进的距离估计算法

对于收发节点之间的信号强度值，本文采用滑动平均滤波算法来获取。通过获得了N=10个连续采样值，其队列长度为N，每次采样到一个新数据放入队尾，根据先进先出原则，扔掉原来队首的一个数据。将队列中的N个数据进行算数平均运算，便可以获得新的滤波结果。该方法能够有效抑制周期性干扰，平滑度较高。

根据滑动平均滤波算法得到的节点间的信号强度值，利用式(1)可以得到路径损耗指数nh的值。

根据路径损耗指数nh和采集到的信号强度值RSSI，以及式(2)，可以得到公式中的参数A的值。

由于RSSI的值是变化的，因此A的值也会发生改变。在得到所有RSSI对应的A的值后，观察A值的变化规律，并得到A与相应数值序号的规律函数

A_fit=f(N)

(5)

式中，N表示数值序号；A_fit表示根据所有获得的参数A的值得到拟合函数的值。

根据A值的变化规律，路径损耗指数n和信号强度值RSSI，并利用式(3)得到的规律，可以得到收发节点之间的估计距离

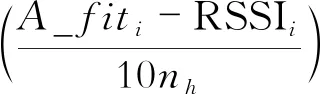
(6)

式中，dh表示节点间的距离。

由于在实际中，A_fit是未知的，因此式(6)需要进一步改进，可以通过RSSI来获得距离。在计算路径损耗指数和参数A的过程中，一部分距离是已知的，根据已知的距离和dh通过加权算法可以获得新的距离

(7)

(8)

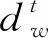
(9)

则根据采集到的信号强度值RSSI，利用公式(9)可以得到节点间的估计距离

dr=10＾(f(rssi))

(10)

式中，f(rssi)表示待测节点与已知节点间的信号强度值的表达式；dr表示根据信号强度值得到的估计距离。

最后，通过MSE、RMSE和MAE 3种误差来评估估计距离dr和LNSM方法得到的距离dl之间的关系。

3 实验

3.1 实验设置

本实验研究了在高铁附近环境中，提高根据节点之间的信号强度值得到距离的精度的问题。由于实验在高铁附近实施，考虑到列车通过时产生的电磁干扰的影响，因此在进行测距实验之前先进行电磁干扰实验。

在本次实验中，终端节点采用了CC2530与GPS集成的传感器模块，该集成模块的使用是为了下一步研究的进行；协调器节点使用了仅带有CC2530芯片的传感器模块。

3.1.1 实验一

首先，使用协调器节点和2个终端节点在铁路旁进行实验，检测无线节点信号传输的干扰情况。将2个终端节点均悬空放置，终端节点与最近护栏间的距离约为7.6 m，终端节点距离铁轨约为10 m，并且，协调器节点与终端节点之间的距离为1 m。

协调器节点与PC机相连，用来显示接收到的数据。协调器节点与终端节点始终保持正常通信状态，当高速列车到来时，从开始听到高速列车到来的声音起，直到列车声音消失，记录列车经过的时间，一直记录6次。

在该实验完成后，为了观测列车到来时信号强度与列车未到时信号强度的变化，在列车到来行使的时间(10 s左右)前后，各增加10 s的时间。则列车到来的有效时间区域是10～20 s。观察RSSI的变化情况，分析列车产生的强电磁是否对终端节点的无线传输有影响。

3.1.2 实验二

在电磁干扰实验完成后，进行测距实验。在测距实验中，采用3个终端节点和1个协调器节点进行实验，并且3个终端节点固定位置不变，与PC机相连的协调器节点在终端节点构成的三角形范围内进行移动。在协调器节点移动的每个位置处，PC机记录200个信号强度值RSSI，一共记录18组。然后将采集到的RSSI进行处理，获得节点之间的距离，最后分析本文算法得到的距离与真实距离的误差，并与LNSM方法进行比较。

3.2 实验分析

在检测终端节点无线传输信号是否受高速列车产生磁场影响的实验中，采用了2个终端节点，观察2个终端节点与协调器之间的RSSI变化情况。如图1所示。

从图1中可以看出，在10～20 s时间内，2个终端节点的RSSI相比较其它时间的信号强度值没有明显的改变。第一个节点RSSI的变化范围是-45～-42，第二个节点RSSI的变化范围是-54～-48，由于模块本身也会对信号强度值RSSI有一定的影响，并且2个节点的RSSI在高速列车经过的时间段之内变化不是很大，因此，本次试验认为高速列车通过时，对终端节点的无线信号传输没有明显的影响。在下面的分析中，不考虑高速列车产生电磁干扰的影响。

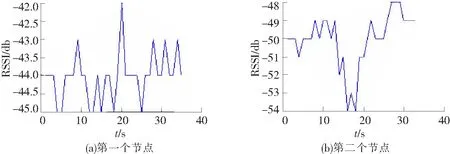
图1 终端节点a和b的RSSI变化情况

图2 d与RSSI的关系图

终端节点在特定位置处采集到的RSSI进行滤波处理，得到图2所示的信号强度值RSSI与距离d的关系图。 根据图2中的关系曲线图可以看出，在5 m之内，RSSI与d具有一定的规律性，但在5 m之后，RSSI随d的变化是不规律的。因此，针对本实验采集到的RSSI，本文分析了5 m范围内RSSI与d的关系，为了得到该环境下的参数，路径损耗指数n和参数A取30 m大范围内的数据进行计算。并通过获得的RSSI，利用本文提出的算法来估计终端节点与协调器节点之间的距离。

利用上述算法，根据节点之间的信号强度值RSSI，可以计算得到它们之间的估计距离，并与LNSM方法在该环境下得到的估计距离进行比较，如图3所示，其中d1表示节点之间实际测量的距离值，d2表示根据RSSI测量计算得到的距离值。 从图3显示的结果可知，在该实验中，由于5 m之后RSSI的不规律性，LNSM方法根据RSSI得到的距离与真实距离相差较大。本文提出的距离估计算法利用RSSI得到的距离比LNSM方法得到的距离更加接近于真实距离，距离的精度更高。为了评价该算法的性能，采用了MSE、RMSE、MAE 3种误差的数据。图4更直观地显示了提出的距离估计算法在该实验环境下的误差。

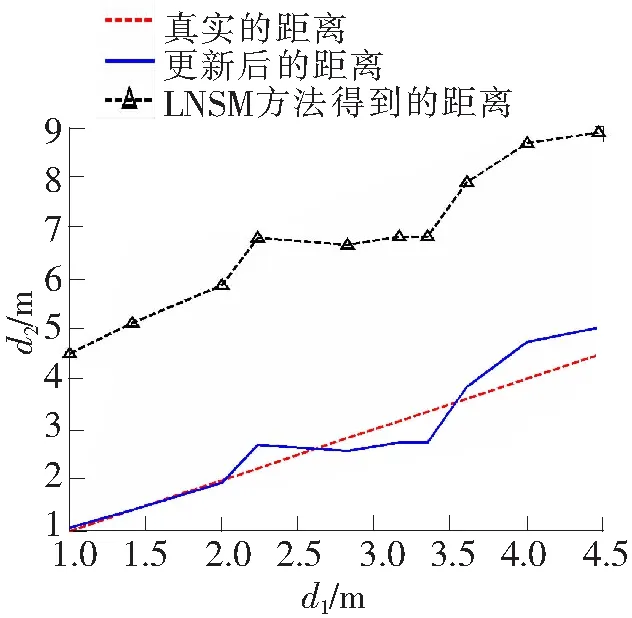
图3 3种距离比较

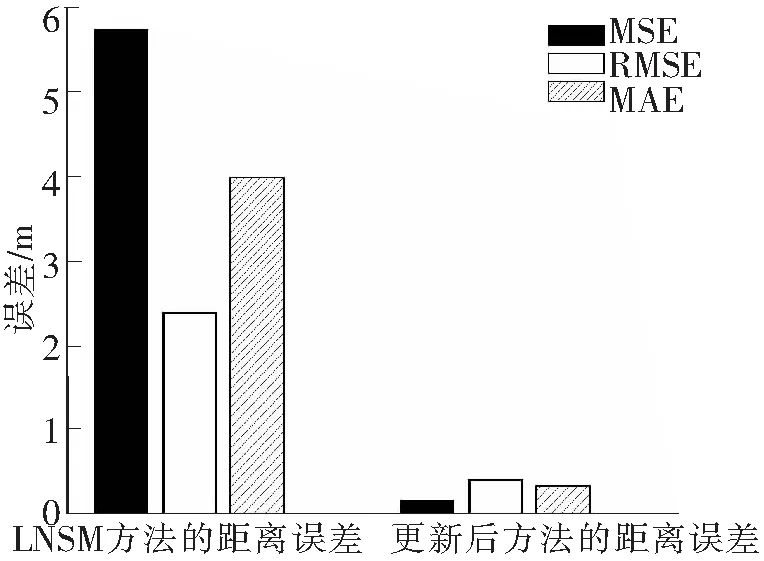
图4 所提算法得到距离的3种误差

在图4中可以清楚地看出，在实验环境内，LNSM方法得到的距离误差较大，MSE、RMSE、MAE 3种误差分别是：5.744 5、2.396 8、3.988 2。本文提出的距离估计算法在该实验环境下，通过RSSI得到的估计距离3种误差均较小，MSE、RMSE、MAE 3种误差分别是0.174 2、0.417 4、0.338 8。并且这3种误差反映了提出的距离估计算法的可行性，能有效地提高距离精度。

4 结语

本文研究了基于RSSI利用相关距离估计算法提高距离精度的问题。在距离估计算法中，加入权重的思想并将经过加权的距离做进一步的变化，得到RSSI与lgd的关系，则在实验环境下，可以根据信号强度RSSI得到节点之间的估计距离。在仿真实验中，将估计距离和LNSM方法得到的距离二者均与真实的距离比较。结果表明，根据RSSI提出的距离估计算法得到的节点间的距离相比LNSM方法得到的距离更逼近真实距离，误差较小。说明了提出的距离估计算法在高速铁路环境下的可行性。

本文的距离估计算法能在5 m范围内获得有效的结果，但如果距离超出5 m，由于RSSI随距离d变化的不规律性，使用普通的算法具有一定的局限性，无法得到有效的距离。下一步将在远距离范围中进行研究，提出有效的算法来提高距离估计的精度。