除霜器噪声特性的仿真研究

邵士前，樊刘杨，豆腾尧，闫伟

(山东大学能源与动力工程学院,山东济南 250061)

0 引言

商用客车作为一种远程交通工具，对乘客的乘坐舒适性要求较高，客车噪声是影响乘客舒适性的重要因素，需要对客车的噪声进行有效控制。客车噪声主要有车内噪声和车外噪声，车内噪声又分为固体声和空气声，其中固体声是车内固体振动产生的噪声，空气声是车内空气波动产生的噪声；车外噪声主要由车身、轮胎与外界空气接触产生。近年来，随着发动机技术的突飞猛进，发动机噪声降低的幅度较大。对发动机之外的部件进行噪声控制是降低汽车噪声另一条重要途径[1]。除霜器作为客车必不可少的部件，是车内噪声的主要来源之一，对其噪声进行有效的控制可以提高乘客的舒适性。在噪声仿真方面，杨博[2]应用稳态雷诺平均那维尔-斯托克斯方法较准确地定位了汽车外部噪声的主要来源。张群峰等[3]对比了分离涡仿真和非线性声学方法仿真腔体启动噪声的效果，找出两者产生差别的原因。徐志超[4]运用混合计算方法，推测发动机进气启动噪声产生的原因。刘厚林等[5]应用大涡仿真方法找出引起离心泵隔舌处压力脉动的主要原因。邓晓龙等[6]应用大涡仿真方法模拟推导汽车暖风通道的噪声特性。

1 研究对象

某款除霜器结构如图1所示，其主要部件为散热器和风扇。散热器下部是网状进风口，上部有3个出风口，2个大出风口直径7.5 cm，一个小出风口直径3 cm。除霜器设计高、中、低3挡。风扇最大转速为2000 r/min，理论通风量为1200 m3/h。除霜器风扇采用鼠笼式风扇，共有2个风扇，每个风扇有28片扇叶。散热器采用翅片式散热器。

声音是由空气的脉动产生。空气在脉动过程中，压力由P0变化为P0+ΔP，ΔP为声压[7]。流体噪声是流体经过物体表面时产生的噪声。流体噪声的噪声源分为单极子声源、偶极子声源和四极子声源[8]3种。单极子噪声由1个点振源产生，偶极子噪声是物体表面共振作用产生的噪声。四极子噪声主要由风扇产生，是风扇在旋转时引起空气涡流破碎而产生的噪声[9]。该除霜器产生的噪声主要是四极子噪声。

a)整体外形 b)内部结构图1 除霜器结构图

Lighthill首次提出流体噪声产生机理，由流体学基本运动方程和连续性方程推导出流体噪声产生的Lighthill机理公式为[10]

(1)

2 建模

2.1 网格模型

对该款除霜器模型做几何处理，简化表面结构。在hypermesh中生成面网格。面网格模型选用三角形网格，共计131万个面网格。将生成的面网格导入STAR CCM+中生成体网格，网格模型选用多面体网格生成器和棱柱层网格生成器，共生成684万个体网格。对风扇区域进行加密处理，以便更好地捕捉细节。棱柱层厚度为2 mm，层数为5层，棱柱层延伸为1.5，并生成计算域。除霜器网格划分模型如图2所示。

a)整体外形 b)内部结构图2 除霜器网格划分模型

2.2 物理模型

对除霜器周围的流体区域选择理想气体作为物理模型，采用非定常仿真，采用气动声学模型中的Ffowcs Williams-Hawkings 非稳态模型和飞行中的 FW-H 模型[11]。涡流模型采用分离涡[12]仿真进行结果对比。分离涡仿真结合RANS方法在近壁面湍流处理的优势和LES处理远离壁面的大涡湍流的优势[13]。对固体区域建立三维恒密度分离固体能量的隐式不定常模型[14]。对散热器区域采用多孔介质模型，其黏性阻力系数为80 kg/(m3·s)，惯性阻力系数为25.0 kg/m4，孔隙率为0.9，湍流黏度比为10。

Ffowcs等[15]于1969年在广义函数理论的基础上推导出FW-H方程，该方程表示流体在由静止到任意运动的过程中噪声的产生方式。FW-H 模型是在流体力学N-S方程的基础上按照非齐次波动方程的规律重新规划整理得到的，能够准确计算流体在由静止到任意运动时产生的噪声，是气动噪声学的基础理论之一。本文中采用飞行中的FW-H模型。假设控制面方程为

f(xi,t)=0,▽f=ni，

式中:ni为控制面上单元的外法线上的矢量方向,Vn表示的是控制面上单元的速度。

FW-H模型最常用的公式为:

(2)

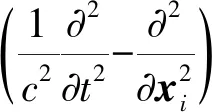
2.3 边界条件

图3 除霜器计算域

在除霜器周围建立1个方形的计算域仿真真实空间，如图3所示。在计算域中建立新的笛卡尔坐标系。计算域进口设置为压力进口，出口设置为压力出口。对于风扇采用MRF模型。在风扇周围设置旋转区域。旋转区域与空气之间以界面形式连接，对风扇采用静网格而不是动网格，可以大大减少计算量，节约计算时间。各边界采用多面体网格形式，为了更好地捕捉细节，边界层层数设为5。各部分的具体属性如表1所示。

表1 边界条件

3 仿真结果分析

3.1 稳态仿真

对除霜器流场先进行稳态仿真分析，通过在进出口建立质量流量报告获得进出口面上的质量流量。当进出口质量流量误差小于0.5%时，认为仿真已经收敛。在稳态分析中，风扇转速分别选用了1500、1750、2000 r/min，得到3种转速下进出口质量流量及误差如表2所示。

表2 不同转速下的进出口质量流量

从表2可以看出，3种转速下进出口质量流量误差均在0.5%以内，可以认为稳态仿真已经收敛。取2000 r/min转速条件下的仿真结果分析除霜器流场，截面x=-20 mm上的速度场如图4所示(图中单位为m/s)。

图4 x=-20 mm截面速度场

从图4可以看出，除霜器在工作过程中，风扇表面气流速度较大，最大达到15.6 m/s。出口处由于截面积突然减小，空气流速急剧增加。散热器处由于具有多孔结构，造成节流效果，空气流速有所降低。

图5所示为稳态仿真中得到的风扇表面空气压力场(图中单位为Pa)，图6为除霜器外壳的空气压力云图(图中单位为Pa)。从图5可以看出，风扇表面空气压力在中心处比较小，在风扇翅片表面处压力比较大，风扇在迎风面上的压力远大于背风面，这是噪声产生的主要原因之一。从图6可以看出，在风机出风口处，空气直接吹到外壳壁面上，外壳出风口处由于截面积减小，导致上壁面空气压力比较大，也是噪声产生的原因之一。

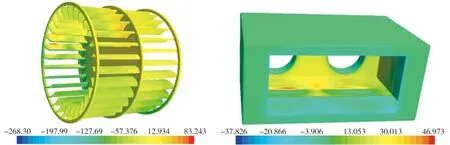
图5 风扇表面压力分布云图 图6 除霜器外壳压力云图

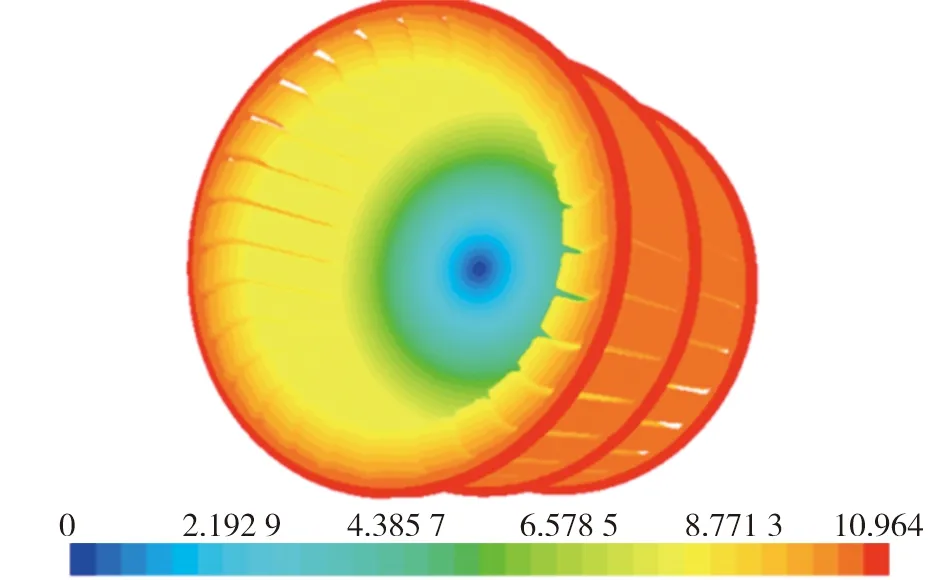
图7 风扇表面速度矢量云图

图7所示为风扇转速为2000 r/min时风扇表面的空气速度矢量图(图中单位为m/s)。从图7可以看出，风扇表面的空气速度从中间向外依次增加，最大速度出现在最外层叶片表面，为10.964 m/s。风扇半径为52.5 mm，经计算可得理论风扇边缘最大速度应为10.99 m/s。仿真结果与理论值误差小于0.1%。

3.2 瞬态仿真

在稳态仿真的基础上，将模型时间改为不定常类型，湍流模型分别应用分离涡模型和大涡模型，风扇转速选用最高转速2000 r/min。在Ffowcs Williams-Hawkings 非稳态模型，应用飞行中的 FW-H 模型，时间步长设为8.33×10-5s，每5步迭代1次，总时长设为1.2 s。使用飞行中的 FW-H 模型时将不渗透面设为风机，风扇表面以及除霜器外壳作为噪声源，在除霜器出口1 m处设置一个接收点，用来接收声压。稳定后进口质量流量为0.499 5 kg/s，出口质量流量为0.498 7 kg/s，误差为0.16%，小于0.5%，说明计算结果收敛。

图8是通过监测点得到的出口1 m处的压力变化曲线，对噪声声压信号在时域内采用等效连续声压级进行分析。傅里叶变换可以将1个时域信号转换成在不同频率下对应的振幅及相位，其频谱就是时域信号在频域下的表现。

图8 出口1 m处的压力变化曲线

对图8中的声压信号进行快速傅里叶变换得到频域内客观声压级曲线，如图9所示。快速傅里叶变换是离散傅里叶变换的一种快速算法。离散傅里叶变换的基本公式如式3[16]所示，数据序列x(n)长度设为M，则定义x(n)的N个点DFT(离散傅里叶变换)为:

(3)

式中N为离散傅里叶变换区间长度，要求N≥M。

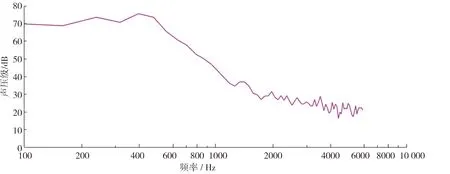
图9 出口1 m处声压级曲线

人对声音的感知与声压变化有关，同时与声音的频率也有关系。A计权声压是根据人体对声音的感知，通过对每个频率上的声压进行加权，得到一个更加符合人体感知的声压曲线。在频域内对A计权声压级[17]

(4)

式中：A1000为1000 Hz对应的声压级；f为计算频率，Hz；f1=20.6 Hz;f2=107.7 Hz;f3=737.9 Hz;f4=12 194 Hz。经计算可得总的A计权声压级为73.34 dB。

将图8经过快速傅里叶变化可得A计权声压频谱图，如图10所示。从图10可以看出，A计权声压在线性计权声压的基础上低频噪声的部分衰减极大，忽略了低频噪声的危害。为了更好地看出噪声分布的频率范围，绘制1/3倍频的A计权声压级，如图11所示。

图10 A计权声压级

图11 1/3倍频A计权声压级

从图11中可以看出，低频噪声的声压级较大，高频噪声的声压级较低。较高的声压级集中在200～900 Hz，最高声压级接近70 dB，出现在500 Hz附近。

3.3 试验验证

试验采用丹麦公司B&K生产的PULSE(声学)材料测试系统，应用配套PULSE 21.0对测试得到的声压进行分析。图12是试验中得到的声压频谱随时间变化得到的map图，测试时间为60 s，测试点在除霜器出口1 m处。

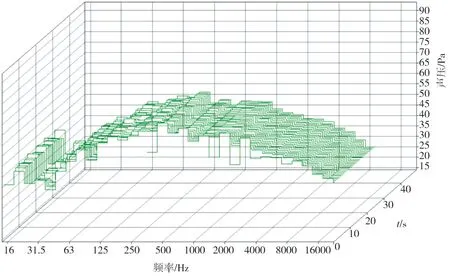
图12 60 s声压频谱随时间变化map图

图13是试验得到的A计权声压级图，图14为仿真得到的A计权声压级图。由图13可以看出试验总的A计权声压级73.4 dB，由图14可以得到总声压级为73.34 dB，误差为0.08%，仿真结果符合真实情况。

图13 试验A计权声压级图

图14 仿真A计权声压级图

图13～14经处理得到1/3倍频A计权声压图，如图15、16所示。

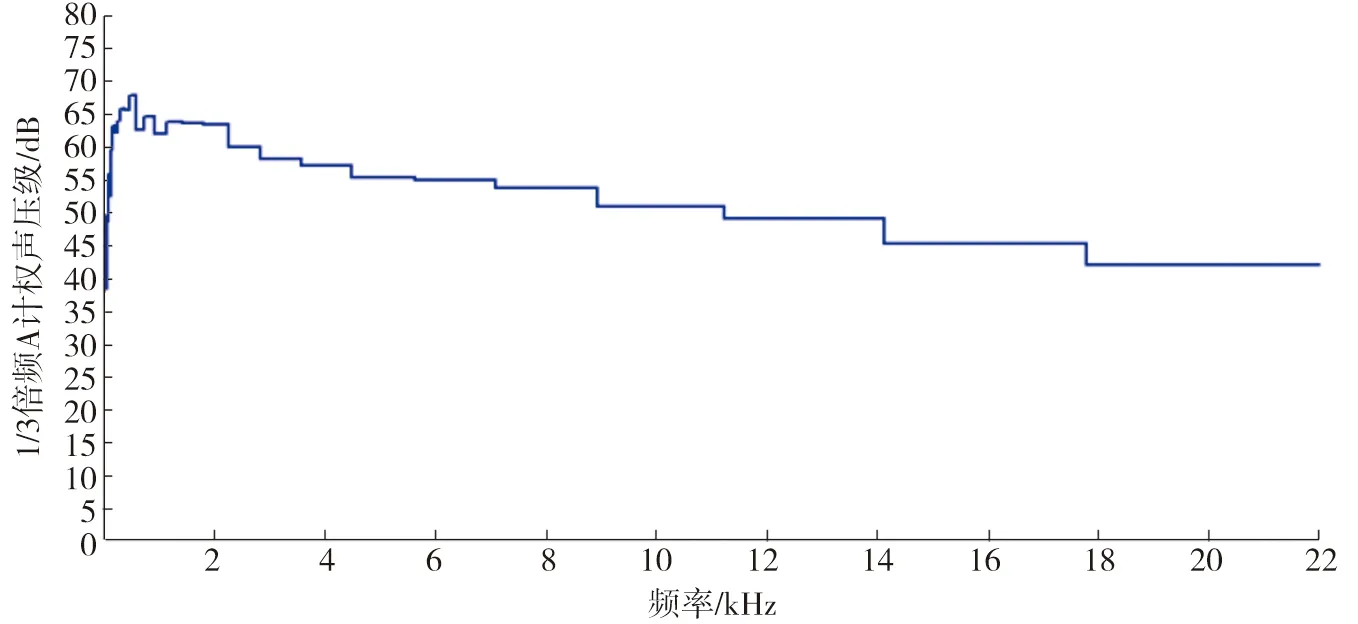
图15 试验1/3倍频A计权声压级图

图16 仿真1/3倍频A计权声压级图

从图16可以看出，在频率150～1000 Hz出现高声压级，这与仿真得到的高声压级分布范围大致相同。最大声压级接近68 dB，仿真结果最大声压级为70 dB，误差为2.9%。从图16中可看出高分贝所在频率为150～1000 Hz。综上所述，仿真结果与试验结果误差在5%以内，仿真方法得到验证。

4 结论

对某款除霜器的噪声进行仿真计算，分析该噪声产生的原因及噪声源位置。利用网格划分软件对除霜器进行划分，再利用STAR CCM+软件对除霜器进行物理建模，通过计算得到该款除霜器在转速2000 r/min时的声压，并通过快速傅里叶变换得到其A计权声压级图，通过试验得到该款除霜器在转速2000 r/min时的噪声数据。

通过对比试验数据与仿真数据中的A计权声压级图以及1/3倍频声压级图，可以看出，仿真结果中高分贝频率为150～1000 Hz，为中低频率，试验结果与其趋势大致相同，误差小于5%。试验得到的总的声压级为73.4 dB，仿真得到的声压级为73.34 dB，误差为0.08%，验证了该仿真方法的可行性。

通过以上分析可知，该款除霜器噪声是风扇噪声与除霜器外壳振动噪声共同组成，下一步可以通过增大除霜器外壳厚度降低振动以及优化风扇翅片等措施来降低除霜器噪声。