新课标两道高考实验试题的参考答案引发的思考——兼谈逐差法减小误差的理论根源的完整理解

王志成

(甘肃省临夏中学，甘肃 临夏 731100)

1 问题的提出

“测定匀变速直线运动的加速度”是高中物理实验中的一个很重要的学生实验,也是高考考查频率极高的一个实验．逐差法是此实验数据处理的基本方法．若给出奇数段实验数据,用逐差法求加速度,就要舍弃其中的一段实验数据．请看以下两道高考题给出的参考答案．

1.1 舍弃最小段数据的高考例证

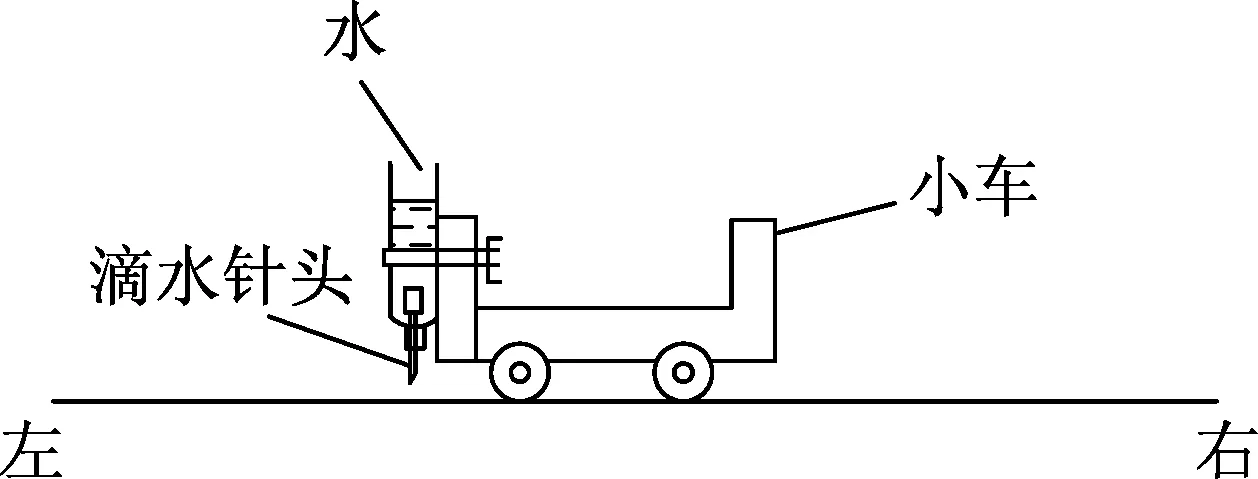
图1

例1.(2017年新课标卷Ⅰ第22题)某探究小组为了研究小车在桌面上的直线运动,用自制“滴水计时器”计量时间．实验前,将该计时器固定在小车旁,如图1所示．实验时,保持桌面水平,用手轻推一下小车．在小车运动过程中,滴水计时器等时间间隔地滴下小水滴,图2记录了桌面上连续6个水滴的位置．(已知滴水计时器每30 s内共滴下46个小水滴)

图2

(1) 由图2可知,小车在桌面上是________(填“从右向左”或“从左向右”)运动的．

(2) 该小组学生根据图2的数据判断出小车做匀变速运动．小车运动到图2中A点位置时的速度大小为____m/s,加速度大小为____m/s2．(结果均保留2位有效数字)

高考参考答案: (1) 从右向左；(2) 0.19，0.037.

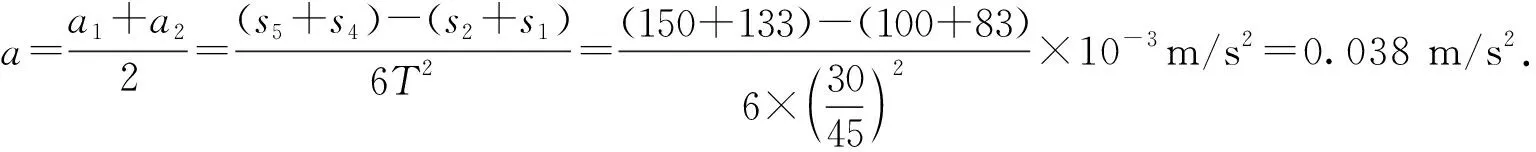
图3

高考参考答案为0.037 m/s2(结果保留2位有效数字)．由此可以推断:舍弃了最小段数据83 mm．

1.2 舍弃中间段数据的高考例证

例2.(2016年新课标卷Ⅰ第22题)某学生用图3所示的实验装置验证机械能守恒定律,其中打点计时器的电源为交流电源,可以使用的频率有20 Hz、30 Hz和40 Hz,打出纸带的一部分如图4所示．

该学生在实验中没有记录交变电流的频率,需要用实验数据和其他条件进行推算．

(1) 若从打出的纸带可判定重物匀加速下落,利用图4中给出的物理量可以写出:在打点计时器打出B点时,重物下落的速度大小为________;打出C点时重物下落的速度大小为________;重物下落的加速度的大小为________．

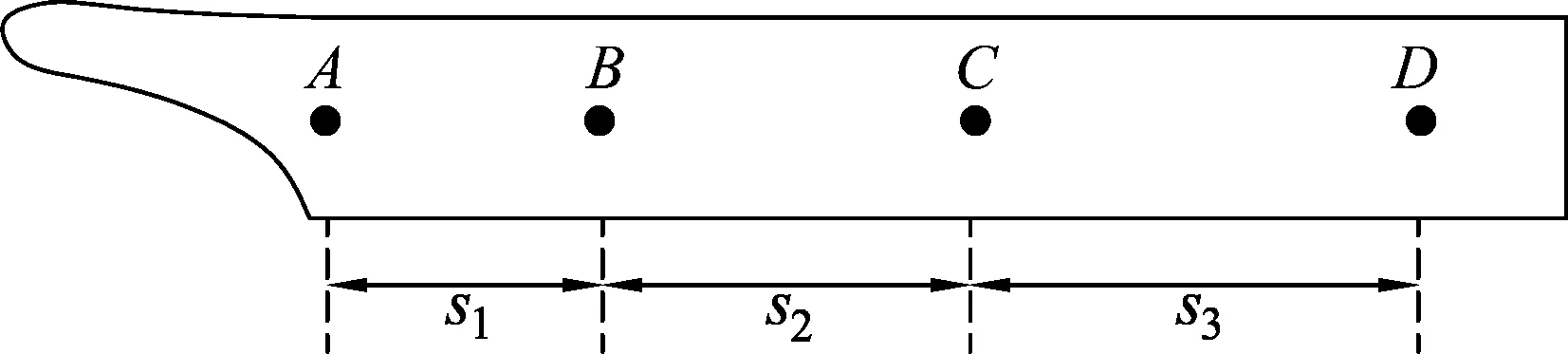
图4

(2) 已测得s1=8.89 cm,s2=9.50 cm,s3=10.10 cm;当地重力加速度大小为9.80 m/s2,实验中重物受到的平均阻力大小约为其重力的1%．由此推算出f为________Hz．

1.3 哪种舍弃法更合理的争论

两次高考参考答案对同一问题(逐差法求加速度),数据处理采用了不同的舍弃法．究竟哪种舍弃法更合理呢?

观点1:舍弃最小段数据．理由是小量的测量不准确,相对误差大．持这一观点的教师较多．

观点2:舍弃中间段数据．理由是各种版本的物理教材对偶数段实验数据应用逐差法时,有一个基本要求,要求求差的差值要大,舍弃中间段数据后求差时差值比舍弃最小段数据求差的差值大．持这一观点的教师少．

彼此都不能说服对方．

其实,单次测量的偶然误差究竟是多大,我们无从知晓．因为偶然误差的来源很多,各实验又有各自的特点,所以很难给出预测偶然误差的统一的规定．在误差理论分析中,一般估计它的最大值．一组等精度单次测量偶然误差,其最大不会超过仪器最小分度值的一半．

例1中,5段实验数据,每一个数据是一个单次测量的,但5个数据又是等精度测量．考虑到中学实验测量纸带常用的是最小刻度(精度)为毫米的直尺,测量时直尺两端的读数误差各取最小分度的一半即0.5 mm．所以,5段实验数据各自单次测量的绝对误差的估计值应取相同值Δs=±1 mm．可见,观点1的理由“小量的测量不准确,相对误差大”的判断正确,所以持观点1的教师多,如文献[1-2]也是这种观点．

笔者认为,相对误差大的一组数据对间接测量加速度的测量误差的影响不一定大．根据误差理论,[3]间接测量的误差不仅取决于直接测量误差的大小,同时也取决于函数(间接测量的计算公式)的具体形式,不同函数的误差传递公式不同．因此,舍弃相对误差大的数据是没有理论根据的,只有通过间接测量的误差分析后,才能判断这两种舍弃法的优劣．

2 不同舍弃法的误差分析

根据任意函数(间接测量的计算公式)的绝对误差传递公式．

对于任意函数Y=F(X1,X2,…,Xm),在考虑误差之后,则为Y+ΔY=F(X1+ΔX1,X2+ΔX2,…,Xm+ΔXm)．

在分析绝对误差时,由于误差本身的正或负是不可知的,因此,上式中各ΔX的系数均取绝对值,即任意函数(间接测量的计算公式)的绝对误差传递公式为

(1)

由于同一次实验的同一条纸带求加速度,加速度的真值是同一个值．舍弃不同段数据测量值(计算出的加速度)不同,但加速度真实值(客观存在值)相同,所以绝对误差大的相对误差也大．因此,比较绝对误差的大小即可．

2.1 舍弃中间段数据的绝对误差

若例1中舍弃中间段数据,则应用逐差法后求加速度平均值的计算公式为

(2)

根据绝对误差传递公式(1),求出用(2)式计算加速度的绝对误差为

(3)

式中Δs=±1 mm.

2.2 舍弃最小段数据的绝对误差

若例1中舍去最小段数据,则应用逐差法后求加速度平均值的计算公式为

(4)

根据绝对误差传递公式(1),求出用(4)式计算加速度的绝对误差为

(5)

式中Δs=±1 mm.

比较(3)式、(5)式可知:舍弃中间段的绝对误差小于舍弃最小段的绝对误差．显然舍弃中间段数据求加速度的方法更合理．例1的高考参考答案是不合理的．例2的高考参考答案是合理的．

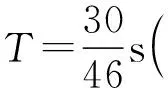
0.039 m/s2．

3 完整理解逐差法减小误差的理论根源

在“测定匀变速直线运动的加速度”的实验中,教师讲解时都要特别强调应用逐差法的两个要点:一要“充分利用实验数据”,二要“求差时差值要大”．强调这两个要点的理论根源是什么?也就是逐差法减小误差的理论根源是什么呢?

3.1 应用逐差法要强调“充分利用实验数据”的理论根源

根据偶然误差的高斯分布规律“绝对值相等、符号相反的误差出现的机会相等”可知,应用逐差法要强调“充分利用实验数据”的理论根源是:多次测量求平均值,以抵消“绝对值相等、符号相反的误差”,从而减小偶然误差．这只是逐差法减小误差的理论根源的一个方面．

例1的分析中,两种不同的舍弃法在充分利用实验数据上是一样的,都用了4个数据．这一点上看两种舍弃法是等效的．

逐差法时充分利用实验数据求加速度和图像法充分利用实验数据画出s-T2图像通过图像斜率求加速度是等效的,两者都能达到充分抵消绝对值相等的正负误差的效果．逐差法的优点在于求解快速,图像法的优点是直观,容易发现、剔除个别错误数据．[2]

3.2 应用逐差法要强调“求差时差值要大”的理论根源

应用逐差法要强调“求差时差值要大”的理论根源,很多教师是不清楚的．

逐差法“求差时要差值要大”的理论根源是间接测量的误差不仅跟直接测量的误差有关,还跟间接测量的计算公式有关,即误差传递公式决定．通过例1的两种不同的舍弃法的误差分析中明显可以看出,间接测量的误差还跟间接测量的计算公式有关．即采用不同的舍弃法计算加速度的公式(2)式和(4)式不同,加速度不同的计算公式的误差传递公式(3)式和(5)式不同．同时也看出,舍弃某一数据后“求差时差值大”的逐差法的误差小．这是逐差法减小误差的理论根源的另一个方面．

例1的分析中,舍弃中间数据求差时的差值要比舍弃最小数据求差时的差值大,从逐差法减小误差的理论根源的另一个方面看,舍弃中间数据产生的误差小．

4 结束语

综合考虑逐差法减小误差的理论根源的两个方面后,例1分析中,两种不同舍弃法的优劣显而易见了．两次高考命题组给出的参考答案采用不同的舍弃法,就是没有完整的理解逐差法减小误差的理论根源所致．

只有完整的理解了逐差法减小误差的理论根源的两个方面,才能在应用逐差法时游刃有余,灵活变通,不会出错．

高考是选拔性考试,试题及参考答案的科学性和严肃性是最基本的要求,只有坚持了科学性和严肃性,才能体现高考的客观性和公正性．