改进的冗余捷联惯组故障检测与隔离主成分析法

2019-09-23袁艳艳

导弹与航天运载技术 2019年4期

叶松，袁艳艳

（北京航天自动控制研究所，北京，100854）

0 引言

惯性器件利用硬件冗余的方式，可以提高运载火箭制导系统的可靠性，如果某个惯性器件出现故障，需要对冗余惯性测量组合进行故障检测与隔离。

基于主成分析法（Principal Component Analysis，PCA）的故障检测与隔离技术已经得到了国内外学者的广泛关注，其实质是一种向量空间变换，将多变量空间转化为子空间，该子空间可以在最小维数下保持原空间的最大方差。从变量优化的角度会发现子空间维数小于原空间的维数，且相互独立。Feng Xu等人提出了一种基于区间观测器和不变集的传感器故障检测与隔离方法[1]，故障检测用于实时故障报警，故障隔离用于检测瞬态性能，仿真结果表明了该方法的有效性。Mania Navi等人研究了主成分析法用于自主水下航行器传感器的故障检测与隔离[2]，仿真结果表明，该方法能用于非线性系统。Walton R. Williamson等人提出了一种用在深空探测卫星上的故障检测与隔离算[3]法，该方法需要通过 Shiryayev序列概率比来测试并计算故障发生的可能性。Kim等人做了开创性研究，提出了两种冗余系统的故障检测方法[4]，一种是结合小波变换的奇偶空间法，另一种是利用阈值确定故障时间间隔并基于模型的故障检测与隔离方法，通过扩展卡尔曼滤波器来估计残差作为检测故障的参考值，仿真结果表明：这两种方法都能用于冗余系统的故障诊断。Alvarez利用主成分析法对废水处理厂的机械进行故障诊断[5]。Daniel Skoogh提出了一种能同时检测不同振幅故障的检测与隔离方法[6]，传感器信号的测量矢量被投影到配置矩阵的正交补空间，通过观察投影点的分布来进行故障诊断。Oliveira在故障检测的数据处理过程中加入中值滤波来消除噪声的影响[7]，仿真结果表明该方法能够检测出微小的阶跃故障信号。Sérgio Brás提出利用状态观测器提供的状态信息来确定不同模型的故障[8]，然而该方法需要箭载计算机具有强大的数据处理能力。张昱君和刘爱伦针对化工生产过程中故障提出了一种改进的主元分析方法[9]，可以检测出对于过程影响较小的故障。考虑到传统的主成分析法对训练数据集之外的数据异常敏感，Yvon Tharrault建立了一个稳健的主成分析模型并使用多故障检测和隔离的结构化残差[10]。主成分析法应用在冗余惯组故障检测研究较少。近年来，Lee and Park提出了一种结合了奇偶向量法的改进主成分析法[11]，该方法能够检测动态环境下的故障信息，但不能进行故障隔离。

本文提出了一种基于广义似然比的改进主成分析法，广义似然算法用来进行故障检测，主成分析法用来进行故障隔离。考虑到加入滤波器能够降低系统的噪声，因此在故障检测前先对奇偶向量进行滤波预处理，目的是能够检测到小幅值故障并具有故障隔离能力。数学仿真结果表明：该方法能够检测小幅值故障并提高故障检测与隔离的效果。

1 经典主成分析法

主成分析法可以被定义为原始数据到新数据的线性变换，并且这些新的数据集相互线性无关。众所周知，传统的主成分析法进行故障检测的方法是将统计量Q和 T2分别与其阈值进行比较，当统计量的数值超过了控制限，就可以判定过程中出现了异常情况。然而这样仅仅能判定在这个时间点出现了故障，而无法判定是哪个部分的异常导致。能够帮助确定哪个部分出现故障工具就是贡献图，它通过每个过程变量对统计量的贡献值来确定。

1.1 T 2统计量

T2统计量反映的是主成分在变化趋势和变化幅值上与模型的偏差程度，计算公式如下：

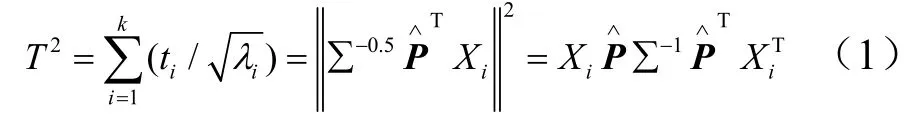
式中 ti为测量样本的第i个主元得分；λi为协方差矩阵的第i个特征值；Xi为第i时刻的采样值；为主元模型的载荷矩阵T2为统计量，是多个变量共同累加的标量，表示数据点到模型中心的距离（建模是经过标准化后中心在原点），因此它的大小反映了新数据偏离正常状态的程度。

如果实际协方差未知，则T2统计量服从F分布，T2统计量阈值为

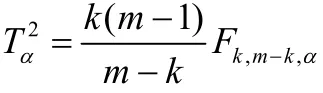
当一个过程变量的信息没有被很好的反映在主元模型中，这个变量出现数据异常情况后通过 T2统计量无法检测到故障，因此在这种情况下需要通过分析测量数据的残差来计算Q统计量。

1.2 Q统计量

Q统计量是平方预测误差，它代表测量值与主元模型的偏差程度。Q统计量的分布如下：

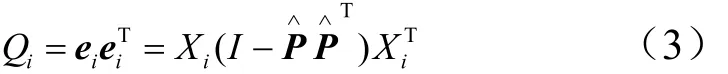
式中 ˆP为由最小二乘法计算得到的载荷矩阵；e为由剩余载荷矩阵生成的误差矢量。

1.3 载荷矩阵计算

载荷矩阵算法也称非线性迭代部分最小二乘算法（Non-linear Iterative Partial Least Squares，NIPALS）。

a）从X中任选一列 Xj，并记为t1，即t1= Xj；

b）计算 P1： P

c）将 P1的长度归一化；

e）将步骤a中的t1与步骤d作比较，如果他们几乎一样，则算法收敛，计算停止，如果它们不一样，回到步骤a；

f） X = X - t1p1T，得到新的误差矩阵，计算其他主元即可。

1.4 主元个数选择方法

采用基于平均特征值的累计方差贡献率法来确定主元个数。累计方差贡献率的定义：矩阵X的协方差矩阵的前k个特征值的和除以它的所有特征值的和（特征值要按由大到小顺序排列），它表示了前k个主元所解释的数据变化占全部数据变换的比例。

式中 control为人为设定的控制限，一般选取 85%，此时满足条件的最大主元个数记为 k1。

接着，计算相关系数矩阵所有特征值的均值，选取大于平均特征值作为主元特征值，同时舍弃掉那些小于均值的特征值，对应的最小的主元特征值的序号记为 k2。

最后，取 k1， k2两者中的最大值为主元个数，即

2 改进的主成分析法

传统主成分析法只能检测出较大幅值故障，本文提出将最大广义似然法应用到传统的主成分析法中，目的是检测小幅值故障。方法的具体流程如图 1所示（以典型的正六面体结构为例）。

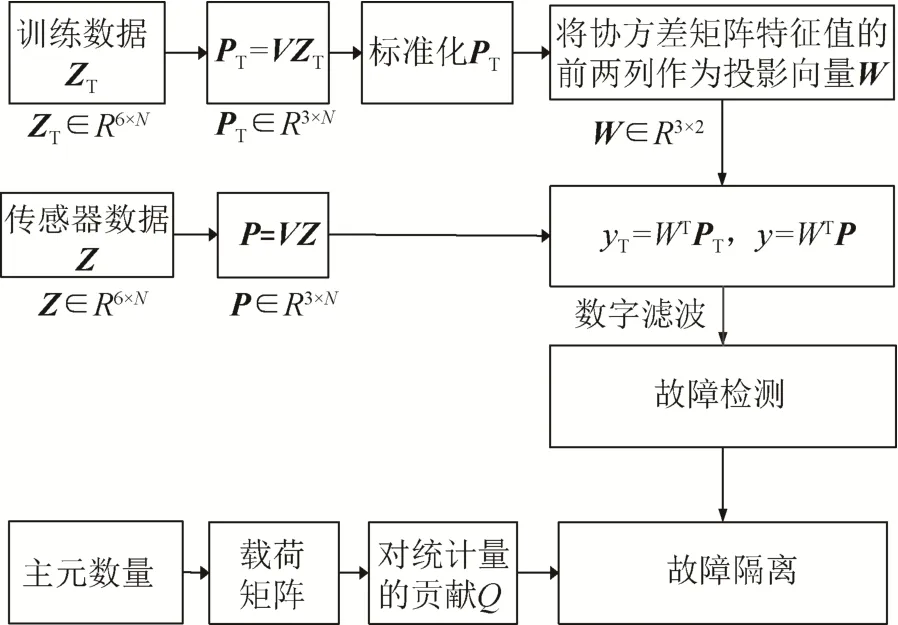
图1 故障检测与隔离流程Fig.1 Flowchart of Fault Detection and Isolation

步骤1：通过安装测量矩阵计算解耦矩阵V，采集正常工作训练数据TZ，得到训练等价向量TP，并标准化后计算计算投影向量W。

步骤 2：应用是将传感器采集得到的数据Z，计算得到等价向量P，再通过投影向量得到Ty。

步骤3：对Ty进行滤波处理。

步骤 4：计算统计量，根据统计量的贡献值进行故障检测。

2.1 广义似然法

冗余捷联惯组含有n个传感器，测量输出只包含测量噪声，那么其测量方程为

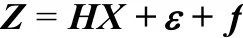
因此，利用矩阵 V可得到等价向量P = V Z = Vε+Vf， P ∈ Rn-3。即等价向量与被测量X是线性无关的，只与误差ε和故障f相关。

根据等价空间原理，解耦矩阵V位于安装测量矩阵H的左零空间，V的秩为 n -3。为了确定V的元素，Potter和Suman建议将V阵选择为具有正对角元的上三角阵，然后通过正交化，便可确定V阵的元素。具体的算法为

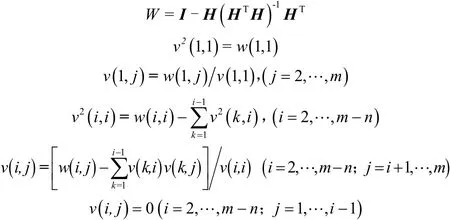
2.2 数字滤波

流程中对Ty进行滤波预处理。众所周知低通滤波器可以降低系统噪声带来的不利影响，而且可以对外来数据不敏感，因此设计的低通滤波器的传递函数为

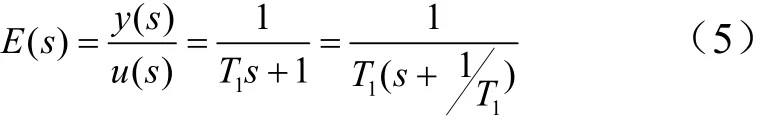
式中1T为滤波器的时间常数。

将式（5）进行Z变换可得：

对式（6）左右进行简化，可以得到一阶滤波器[16]的最终表达式为

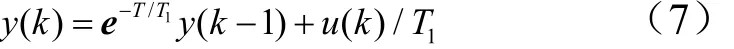
滤波器的参数影响滤波器性能的关键因素，如何选取一个合适的滤波器参数是非常重要的。一方面滤波器参数反映了系统的响应速度，另一方面反映的是系统对于高频信号的衰减，因此滤波器参数的选取是一个需要折中的问题。文献[16]里面的相关研究，选取的一阶滤波器的参数为 0.434。此时滤波器的差分方程如下：

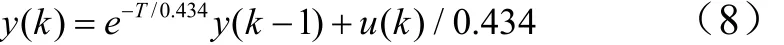
3 仿真分析

3.1 仿真条件

分别对两种配置结构（正六面体结构和三正交二斜置[15]结构）进行仿真分析。

陀螺仪的误差参数如表1所示。

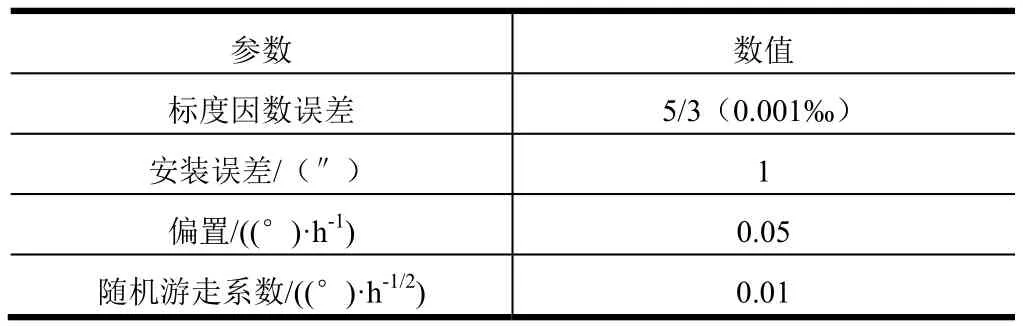
表1 惯组误差Tab.1 Error Parameter

仿真条件如下：在400 s的时候给第5支陀螺仪加入1（°）/h的常值故障。

3.2 PCA方法仿真

3.2.1 正六面体

利用图 1的流程，对正六面体冗余惯组进行仿真分析，结果如图2、图3所示。

图2 特征平面的投影点的分布Fig.2 Projection of Feature Plane

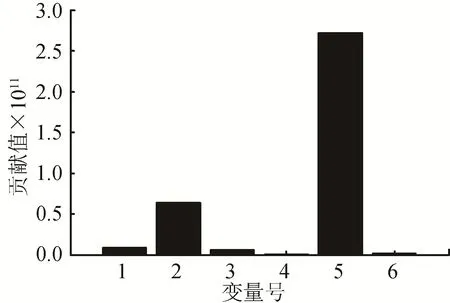
图3 各个变量对统计量Q的贡献值Fig.3 Contribution of Each Variable to Statistics

3.2.2 三正交二斜置

同样三正交二斜置的惯组配置进行了仿真，结果如图4、图5所示。

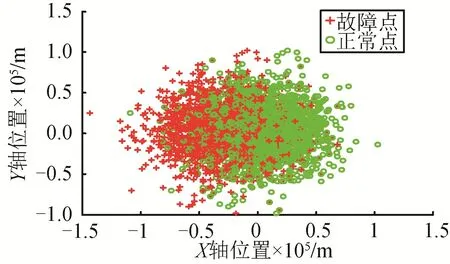
图4 特征平面的投影点的分布Fig.4 Projection of Feature Plane

图5 各个变量对统计量Q的贡献值Fig.5 Contribution of Each Variable to Statistics

从图2和图4可以看出：待检测数据和正常数据在特征平面上的投影没有完全分开，说明原PCA方法检测出1（°）/h幅值的故障困难。并且投影点在X轴的位置和Y轴的位置随时间变化曲线可以看出有故障发生，但是不明显，然而图3和图5表明故障隔离效果较好。

3.3 改进PCA算法仿真

3.3.1 正六面体

为了检验加入滤波器之后的故障检测性能，得到的仿真结果如图6、图7所示。

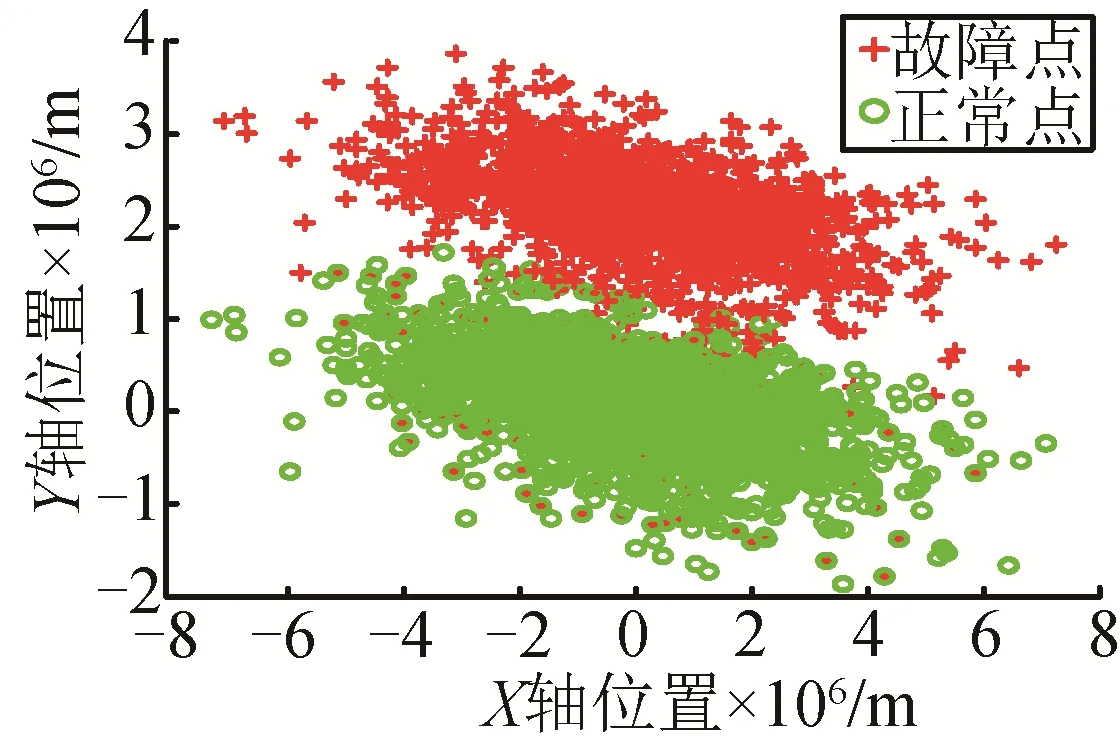
图6 特征平面上的投影Fig.6 Projection of Feature Plane

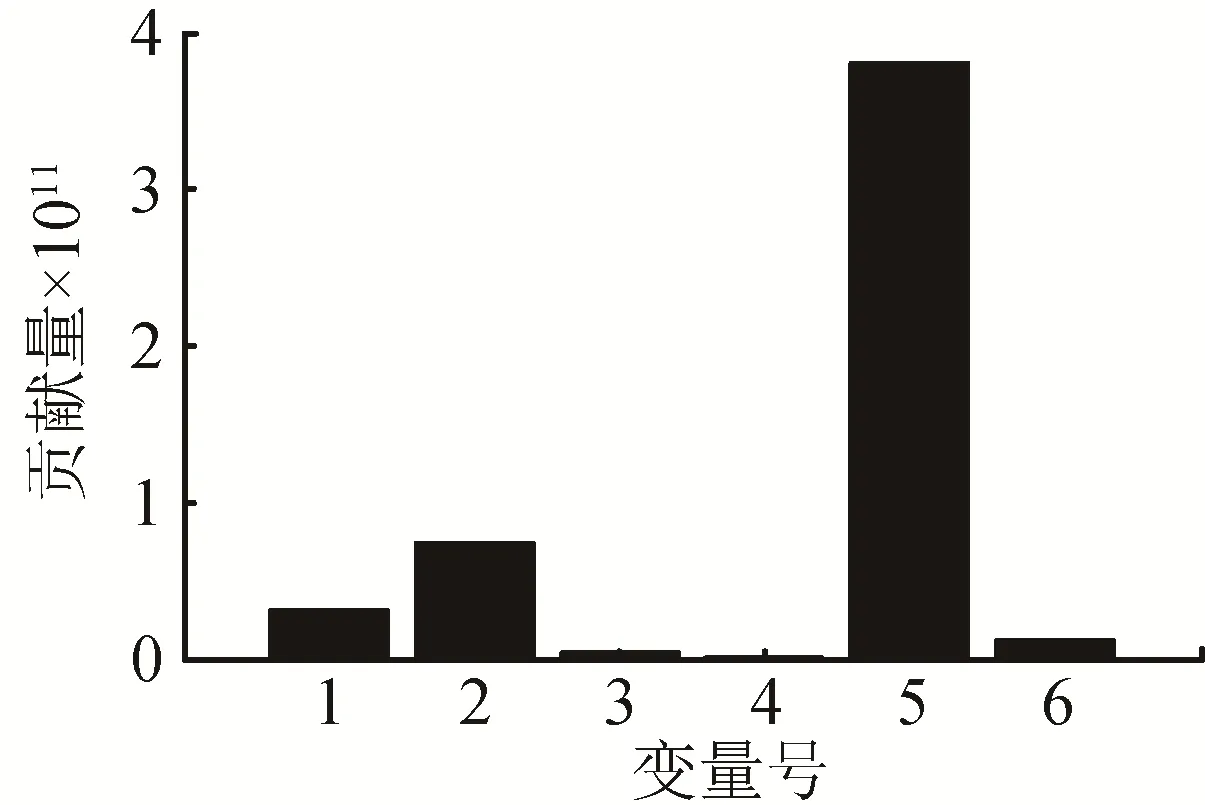
图7 各个变量对统计量Q的贡献值Fig.7 Contribution of Each Variable to Statistics

3.3.2 三正二斜

三正交二斜置的惯组配置的仿真结果如图8、图9所示。

图8 特征平面上的投影Fig.8 Projection of Feature Plane

图9 各个变量对统计量Q的贡献值Fig.9 Contribution of Each Variable to Statistics

图6 代表的是投影位置，可以看出过程中是否发生了故障，可看出正常数据的投影点和待检测数据的投影点分开，说明已经检测到了故障，没有完全分开是因为故障只发生了一段时间而非整个过程（在400 s处发生故障）。从图7可以看出第5个传感器对统计量Q的贡献值最大，因此可以断定第5个传感器发生了故障。图3和图7有细微的差异（各个变量对统计量Q的贡献量数值不完全一致），这是由于陀螺仪误差项包含有随机误差，而故障隔离的结果是正确的。同理，对于三正交二斜置的安装方式也有相同的结论。