北京市长期电力需求预测研究
2019-09-20闫宁
闫宁


摘要:对电力需求准确评估,是电力工业发展方向和速度的重要参考,预测的准确与否,关乎到电力行业的平稳发展以及国民经济的可持续发展。针对北京市电力需求,文章采用了协整分析和情景分析结合的研究方法,结合二者优点,得到北京市未来的电力需求预测结果。
Abstract: Accurate assessment of power demand is an important reference for the development direction and speed of the power industry. The accuracy of the forecast is related to the steady development of the power industry and the sustainable development of the national economy. In view of the power demand in Beijing, this paper adopts a combination of co-integration analysis and scenario analysis, and combines the advantages of both to obtain the future power demand forecast results of Beijing.
关键词:协整;情景分析;电力需求预测
Key words: cointegration;scenario analysis;electricity demand forecast
中图分类号:F426 文献标识码:A 文章编号:1006-4311(2019)23-0066-03
0 引言
电力行业是国家经济命脉,是国家经济发展的基础行业,电力行业的发展关系到国家经济的平稳发展和社会的不断进步,是整个国家最根本的行业之一。其发展速度反映着社会经济水平的发展速度,对电能稳定供应、建设智慧型的坚强智能电网,并大力推进与智能电网结合的泛在电力物联网是我国电力发展的阶段目标[1-3]。对电力需求准确评估,是电力工业发展方向和速度的重要参考,预测的准确与否,关乎到电力行业的平稳发展以及国民经济的可持续发展[4]。
电力需求预测是根据电力负荷、经济、社会等所有相关的历史数据,来探索电力需求历史数据变化规律,寻求电力需求与各种相关因素之间的内在联系,从而对未来的电力需求进行科学的预测[5,6,7,8]。
1 电力需求预测理论及影响因素分析
1.1 协整检验
协整检验就是为了辨别回归是否为伪回归,所谓伪回归,是在利用最小二乘法回归分析时决定系数R2很接近1同时,DW值很小的现象。其特征为在回归分析时,每个变量间的相关系数都较大,足以判断其因果关系,但实际上其结果不可靠,变量间不存在任何因果关系。
协整的定义为:假如存在某些序列x1t,…,xnt,皆为d阶单整序列,记为I(d),并存在向量α=(α1,α2,…,αn)使得αXt~I(d-b),并且d?叟b?叟0,Xt=(X1t,X2t,…,Xnt)',则称时间序列x1t,…,xnt是b阶协整,α为协整向量。
若存在某两个或多个同阶时间序列的线性组合,它们之间通过计算能够获得一个稳定的误差序列,即非平稳时间序列的短期波动不会影响到序列间的长期均衡关系,即可说明序列间存在协整关系。协整检验根据时间序列是否为两条的多少可以分为两类,Engle-Grange两步检验法一般用于两条序列间的协整检验中;而多个时间序列间的协整检验一般采用向量自回归的检验方法,该方法由Johansen建立。
1.2 情景分析法
情景分析法(Scenario analysis method)是基于未来的多样性的一种分析方法,通过对未来可能出现的情景,并分析导致该情景的各种因素是情景分析法的核心思想,可以理解为情景分析法就是构建可能的未来、并进行分析的过程。通过对情景的研究,基于现有的条件和合理的推测,可以分析影响时间的外部因素、对不同政策、规划、技术等对未来发展趋势产生的影响和效果进行定性與定量相结合的系统分析,并以此来对影响情景发生的各种因素进行识别和分析。
1.3 影响因素分析
1.3.1 地域经济发展 地域经济长期稳定的发展电力工业的核心需求,地域的经济发展规模可以直观地当地生产行为、居民生活对电力供应量和稳定性的需求。地域的经济发展根据类型可以分为三类,分别为投资、消费、外贸。一个地域内经济的合理稳定发展会增强地域对临近地区乃至全国地区的劳动力和人才的吸引力,人口规模的增加可以大量推动对电力的需求。
1.3.2 城市化 城市化的主要影响是省市常住人口和流动人口的增加,同样会导致对电力的大量需求。另一方面,大量且快速的人口增长势必导致相应配套设施的增加,政府工程的规划实施速度也会相应增加以提高电力供应能力。但城市化带来的环境问题会导致地方政府加大环境治理,对一些高排放的企业加以整治,因此当城市化到一定程度后电能的需求会放缓。
1.3.3 产业结构 是指其由以农业为主的传统乡村型社会向以工业和服务业等非农产业为主的现代城市型社会逐渐转变的历史过程。产业的升级转型势必导致当地对能源的需求量的增加。
2 北京市电力需求预测模型
2.1 向量自回归模型
向量自回归模型(Vector Auto-regression Model,VAR)是一种较为经典的非结构化的建模方法。具体的看,VAR模型把系统中每个内生变量作为系统中各个内生变量的滞后项的函数来建立模型,其表达形式为:
式中,Yt和分别为k维内生变量向量和滞后内生变量向量,为d维外生变量向量和滞后外生变量向量,p和r分别为内生变量和外生变量中的滞后阶数。Ai为k×k维系数矩阵,Bi为k×d维系数矩阵;显然,系数矩阵也就是待估计的参数矩阵。εt为k维随机误差项所组成的向量,但元素之间可存在同期相关性,但不可存在与自身的滞后项相关和不能存在与模型右边变量的相关。
向量自回归模型中每个方程的右侧都为前定变量,不存在非滞后的内生变量,并且每个方程右边的变量是一致的,因此,可使用最小二乘法估计得到与VAR模型的参数一致和有效的估计量。其中,对于滞后长度p和r的选择上,普遍使得滞后阶数可以足够大进而可以较出色的反映构造模型的动态特征。但对于模型来说,随着模型中的滞后数的增大和待估计参数的增多,模型的自由度随之降低;因此,通常运用AIC信息準则和SC准则的取值最小原则来获得模型的最佳滞后阶数。
2.2 Johansen协整检验
Johansen协整检验方法是以向量自回归模型为理论基础对回归系数的检验,主要用于三个以及三个以上的变量。
设p阶向量自回归模型为:
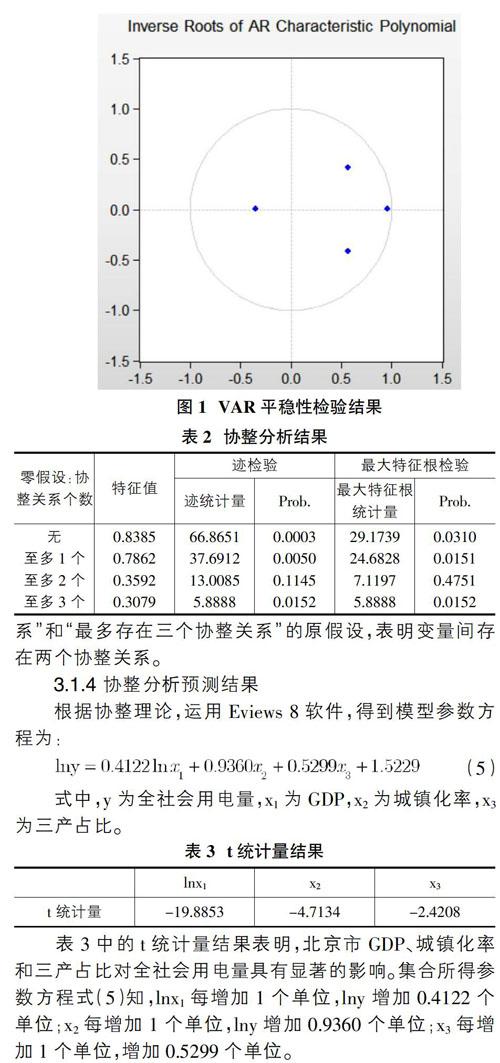
式(3)中。Johansen协整检验的主要机理是分析矩阵∏的秩r 3 分析结果 北京市是我国的首都,分析北京市电力需求的影响因素及其作用效果,对进一步研究全国其他地区的电力需求影响因素具有重要的代表意义。 3.1 协整分析结果 文章主要根据北京市2000-2017年GDP、城镇化率、三产占比、全社会用电量的历史数据,研究GDP、城镇化率、三产占比这三个因素对于北京市全社会用电量的影响,并据此进行协整分析得到参数方程如下式: 式中,y表示全社会用电量,x1表示GDP,x2表示城镇化率,x3表示三产占比,a1、a2、a3分别代表各因素对于y的影响系数,c代表常数项。 3.1.1 ADF单位根检验 采用ADF单位根检验方法对北京市2000-2017年GDP、城镇化率、三产占比进行数据平稳性检验,所得结果如表1所示。 根据表1分析可知,各变量的原序列均为非平稳时间序列,但其一阶差分序列都是平稳的,即各变量都是一阶单整序列,记为I(1)。根据平稳性检验结果,所有序列都是同阶单整的,具备进行协整检验的条件,文章接下来运用协整检验方法验证变量间的长期均衡关系,即协整关系。 3.1.2 VAR平稳性检验 根据SC准则,所构建的包含四个变量的VAR模型的最优滞后阶数为1,在该滞后阶数下,VAR模型的稳定性检验结果如图1所示。 由图分析可知,所有自回归根(AR Roots)都在单位圆内,表明文章所构建的包含四个变量的一阶VAR模型具有良好的稳定性。 3.1.3 Johansen协整检验 同阶单整的时间序列变量线性组合是平稳的,那么可以称各变量之间存在协整关系。协整检验的方法有两种:EG两步法和Johansen检验法,由于EG法估计量在样本数据时是有偏的,同时在多变量协整检验中,结果可能是各自变量是协整,自变量与因变量并不协整,对于结论得出影响较大,因此文章选用Johansen协整检验。 根据VAR模型结果,设定Johansen协整检验之后阶数为VAR模型滞后阶数减1,数据生成过程根据SC准则确定,据此进行Johansen协整检验,结果如表2所示。 由表2可知,在5%的显著性水平下,迹检验和最大特征根检验结果均显著拒绝“不存在协整关系”和“最多存在一个协整关系”的原假设,同时接受“最多存在两个协整关系”和“最多存在三个协整关系”的原假设,表明变量间存在两个协整关系。 3.1.4 协整分析预测结果 根据协整理论,运用Eviews 8软件,得到模型参数方程为: 式中,y为全社会用电量,x1为GDP,x2为城镇化率,x3为三产占比。 表3中的t统计量结果表明,北京市GDP、城镇化率和三产占比对全社会用电量具有显著的影响。集合所得参数方程式(5)知,lnx1每增加1个单位,lny增加0.4122个单位;x2每增加1个单位,lny增加0.9360个单位;x3每增加1个单位,增加0.5299个单位。 3.2 情景分析 根据北京市用电影响因素的历史发展趋势,利用情景分析法,对北京市用电需求的影响因素进行预测,从而进一步对北京市电力需求进行预测。其中影响因素特征描述如表4所示。 由此可得不同情景下北京市用电需求中长期预测结果如图2和表5所示。 由上述分析可以看出,随着GDP、城镇化率、三产占比的提高,北京市电力需求不断上升;同时影响因素增长较快的情景下,北京市电力需求增长也较快。 4 总结 针对北京市电力需求的预测,文章采用了协整分析和情景分析结合的研究方法,通过协整分析,得到北京市全社会用电量在GDP、城镇化率、三产占比影响下的参数方程,并根据情景分析,得到不同因素的未来发展水平,结合协整分析所得的参数方程得到北京市2018-2030年的全社会用电量预测结果。 参考文献: [1]赵会茹,赵名锐,李娜娜,李付强,胡娱欧.基于协整理论的北京市电力与经济增长关系研究[J].陕西电力,2015,43(05):60-64,70. [2]魏晓萌.北京市电力需求影响因素及预测研究[D].北方工业大学,2018. [3]汪斌,张欣欣,嵇灵,解玉磊.北京市电力消耗驱动因素分析及需求预测[J].中国电力,2018,51(06):178-184. [4]陈树民.我国电力需求影响因素研究[D].山东大学,2018. [5]刘俊,赵宏炎,刘嘉诚,潘良军,王楷.基于协整-格兰杰因果检验和季节分解的中期负荷预测[J].电力系统自动化,2019,43(01):73-80. [6]孙伟,鲍毅,戴波,卢君波,王昆.基于改进极限学习机的电力需求预测研究[J].计算机与数字工程,2019,47(04):806-811,819. [7]陈海兰,高学东.基于波动特征的时间序列相似性度量及聚类分析[J/OL].统计与决策,2019(11):17-22. [8]林勇,麻敏华,靳冰洁,黄红伟,张德亮.基于多元相关性矩阵的中长期负荷预测方法研究[J].电气应用,2019,38(01):90-94.
