AZ31镁合金棒材循环扭转变形及其对力学性能的影响

2019-09-19宋广胜纪开盛张士宏

材料工程 2019年9期

宋广胜，纪开盛，张士宏

(1沈阳航空航天大学材料科学与工程学院，沈阳110036；2中国科学院金属研究所，沈阳110016)

镁合金因其具有密度低、比刚度高和电磁屏蔽性好等优点，在航空航天、汽车和电子等产业中具有潜在应用价值，镁合金性能的改善和成形工艺的开发长期受到关注。但镁合金室温下能够独立启动的滑移系少，导致其室温下变形呈现低的强度和塑性，不利于其进行大变形的塑性加工，也难以满足结构件的力学性能要求。相关研究采用异步轧制(differential speed rolling，DSR)和等通道挤压(equal channel angular pressing，ECAP)等特殊变形方式来削弱镁合金型材的基面织构强度[1-4]，以求提高其力学性能。现阶段，采用微合金化手段开发稀土镁合金成为镁合金研究的热点[5-7]，相关研究获得了力学性能明显改善的镁合金型材。

镁合金零件在服役过程中可能受到拉伸、压缩或扭转等载荷的作用。目前，镁合金型材的力学性能及相关机理研究主要集中于常规拉伸或压缩变形[8-12]，扭转变形的研究多集中于单向扭转变形[13-18]，而循环扭转变形的研究相对较少。

关于镁合金扭转变形的力学性能的研究，Song等[13-14]对镁合金棒材进行单向扭转的预变形，发现扭转变形增加了位错密度及削弱了原始的基面织构，明显地提高了棒材的强度和降低了拉压不对称性；Guo等[18]对轧制镁合金进行了大应变的扭转变形，发现当扭转轴与法线方向一致时，扭转试样沿轴向伸长，而当扭转轴与轧向一致时，扭转试样则沿轴向缩短，上述现象是由拉伸孪晶效应所致；Zhang等[19]对镁合金薄壁管材进行了轴向载荷为零和不为零两种条件下的循环扭转变形，发现对于轴向载荷为零的纯扭转变形，虽然拉伸孪晶在大应变幅度下启动，但应力-应变滞回线仍呈严格对称性，而对于轴向载荷不为零的扭转变形，由于孪晶和解孪晶的交替发生，导致切应力-切应变滞回线成非对称性；Yu等[20]对镁合金薄壁管在不同轴向载荷条件下的循环扭转变形的疲劳特性进行了研究，发现轴向拉应力能降低扭转疲劳寿命，而轴向压应力则明显提高疲劳寿命；Albinmousa等[21-23]通过对镁合金管材施加不同比例和不同相差角的轴向和扭转载荷，系统研究了滞回线形状与变形机制的关系，发现孪晶是上述变形过程中一种重要变形模式，纯扭转载荷下滞回线呈严格对称性，轴向和扭转载荷的比值对疲劳寿命无明显影响。

上述研究主要是针对镁合金棒材的单向扭转变形和镁合金管材的循环扭转变形，对于镁合金棒材的循环扭转变形的力学性能和微观机制及其对棒材力学性能的影响则缺少相关的研究。本工作对镁合金棒材进行循环扭转变形，分析了变形过程中的宏观力学性能以及扭转变形对棒材的织构、微观组织和力学性能的影响。

1 实验材料与方法

实验材料采用直径为26mm的商用AZ31镁合金挤压棒材，其化学成分(质量分数/%)为Al 2.68，Zn 0.75，Mn 0.68，Cu 0.001，Si 0.03，Fe 0.003，Mg余量。挤压棒材经过420℃/6h的退火处理后，加工成如图1所示的标准扭转试样。扭转变形在SANS-CTT1202型微机控制电子扭转试验机上进行，扭转变形的速率为34.4(°)/min，扭转变形过程中，试样在轴向可自由移动。扭转变形的最大扭转角分别设为±90°和±60°两种，最大正扭转角对应着顺时针扭转，绝对值最大的负扭转角则对应着逆时针扭转。单个扭转变形周期定义为扭转角自0°开始，顺时针扭转达到正的最大扭转角，然后逆时针扭转变形到绝对值最大的负扭转角，最后顺时针扭转变形到扭转角为零。分别对6个试样进行扭转变形，其中5个试样的扭转参数为：最大扭转角为±90°，总周期数依次为1，5，10，15和20；第6个试样的扭转参数为：最大扭转角为±60°，总周期数为20。

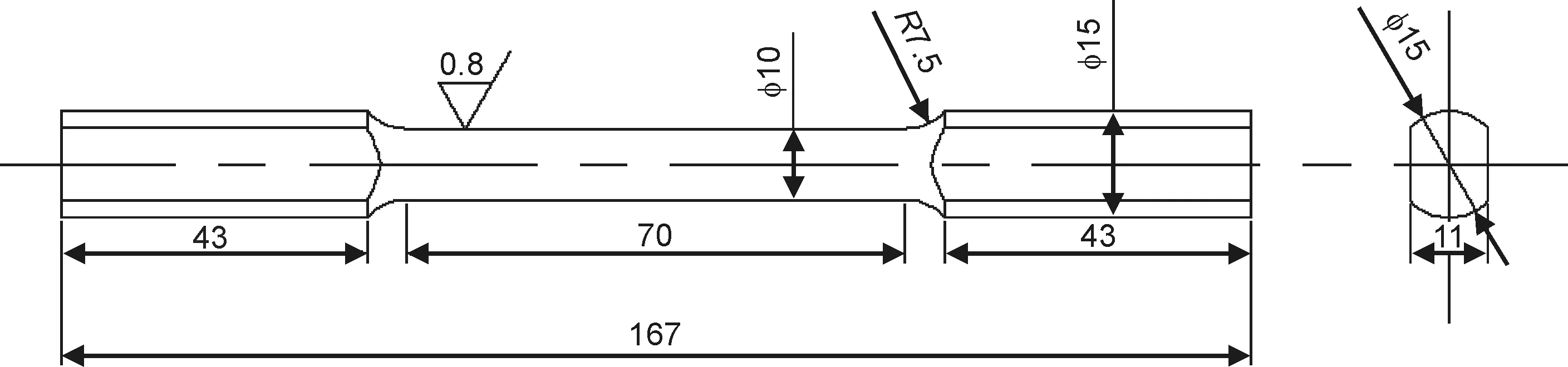
图1 扭转试样Fig.1 Torsion specimen

压缩变形试样为φ10mm×10mm的圆柱体，试样取自扭转试样的轴向中间位置处，压缩试样的轴向与扭转试样的轴向一致，压缩变形在SANS-CMT-5105微机控制电子万能试验机上进行，沿轴向压缩变形，应变速率为10-3s-1。在采用EBSD技术测定晶粒取向的实验中，先对试样进行研磨，再对试样进行机械抛光，最后进行电解抛光，电解液为体积比是1∶9的高氯酸和乙醇的混合液，用液氮将电解液降温到约-20℃时再进行电解，电解电压为15V，电解时间为150s。EBSD实验在附有EBSD系统的Zeiss Gemini SEM500/300场发射扫描电镜上进行，所测得晶粒取向数据利用HKL Channel5软件进行处理。

挤压棒材的宏观极图采用Bruker D8 3KW型X射线衍射仪测得，选用纯铜靶材，样品旋转范围：α=0°～70°，β=0°～360°。采用步进式扫描方式(Δα=5°，Δβ=5°)，利用纯镁粉末对所测得极图的数据进行修正，最后导出所测得XRD数据，采用Mtex软件绘制完整极图。

2 结果与分析

2.1 应力-应变滞回线

对于扭转变形过程，材料扭转试验机采集的主要数据为扭转角和扭矩，分别依据公式(1)和(2)将扭矩转换为名义应力τ，扭转角转换为应变γ。

(1)

(2)

式中：d0,Le，T和φ分别为扭转试样标距部分的直径，标距部分的长度，所测得的扭矩和扭转角。

利用扭转试验机的采集数据，依据公式(1)和(2)得到的镁合金棒材循环扭转变形过程中的应力-应变滞回线如图2所示，可以看出滞回线呈现对称性，曲线在应力为零处出现了水平直线段，这是因为扭转试样在设备上为非紧固连接，导致设备在扭转角为零处改变扭转方向时有短暂的空载，从而引起滞回线上出现如图中所示的应力为零的水平段。图2(b)，(c)显示，对于扭转总周期数小于10的循环扭转变形，在滞回线上的第1周期内的峰值应力低于其他周期，表明加工硬化导致峰值应力增加，而图2(d)～(f)则表明，当循环总周期数达到或高于15时，后继的若干周期的峰值应力低于第1周期的峰值应力，这是材料内部产生微裂纹所导致的。

图2 循环扭转过程中的剪切应力-应变滞回线(a)单周90°；(b)5周90°；(c)10周90°；(d)15周90°；(e)20周90°；(f)20周60°Fig.2 Shear stress-strain hysteresis loops during cyclic torsion(a)90° with one cycle;(b)90° with five cycles;(c)90° with ten cycles;(d)90°with fifteen cycles;(e)90° with twenty cycles;(f)60° with twenty cycles

为分析扭转滞回线在不同扭转周期内的硬化特征，分别选取了总周期数为20而最大扭转角分别为±90°和±60°的若干周期内的滞回线，如图3所示，第1周期内的滞回线显示了单调硬化特征，而从第2周期开始，滞回线的硬化速率呈现波动特征，即当扭转应变的绝对值大约大于4时，硬化速率呈现上升趋势，单个周期内的滞回线在横轴的上半部或下半部分的形状特征与拉伸孪晶启动的应力应变曲线相似，即呈现S型特征曲线，这意味着从第2周期开始，拉伸孪晶开始启动。

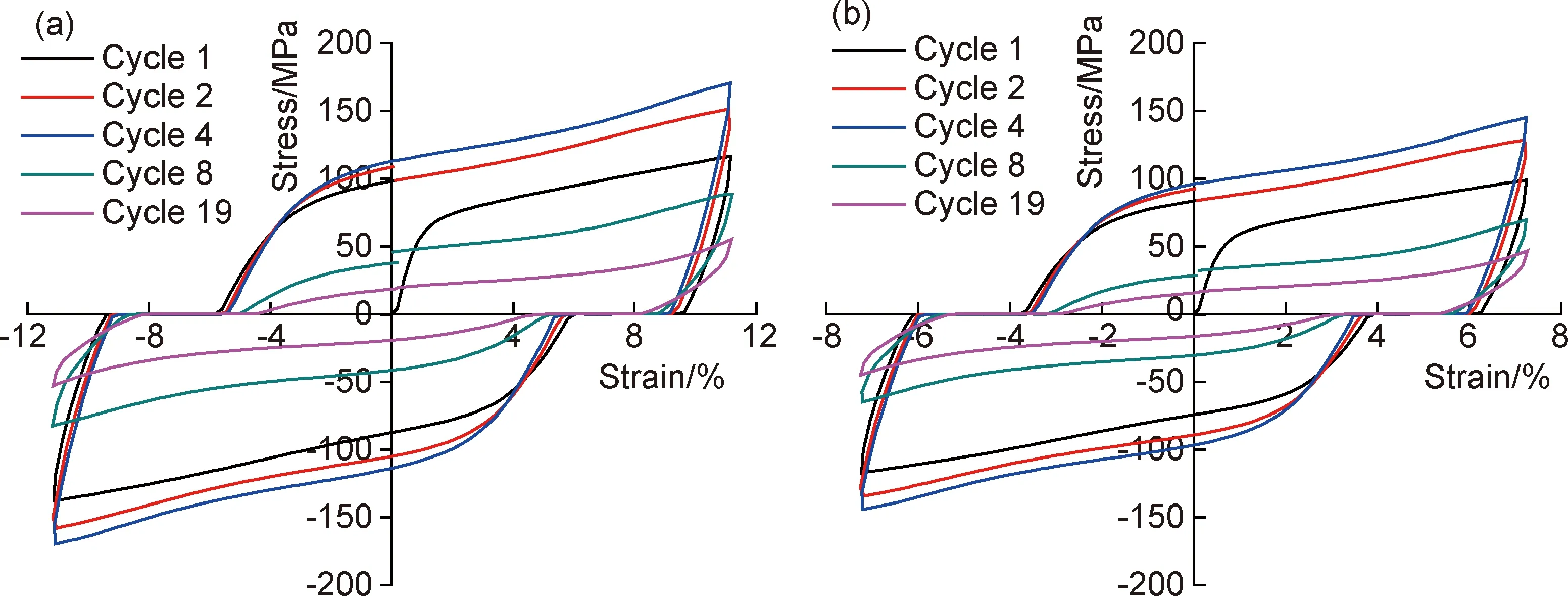
图3 循环扭转过程中不同周期内的应力-应变滞回线(a)±90°扭转；(b)±60°扭转Fig.3 Stress-strain hysteresis loops at different cycles of cyclic torsion(a)±90° torsion；(b)±60° torsion

将图3中不同周期内的滞回线对应的峰值应力进行对比，可以看出，对于最大扭转角分别为±90°和±60°的循环转变形，从第1周期至第4周期，随着周期数的增加，峰值应力是递增的，但是从第4周期至第19周期，峰值应力则递减，并且随着峰值应力的降低，滞回线所包围的区域的面积明显减小。

图4显示了最大扭转角分别为±90°和±60°的循环扭转过程中，峰值应力随着周期数的增加而产生的变化，考虑到循环扭转过程中滞回线呈对称性，故只选取了对应正的最大扭转角的峰值应力进行分析，图中显示峰值应力在第4周期内达到最大值，而后由于裂纹的产生使峰值应力快速下降，当扭转周期数达到8时，峰值应力又呈现慢速下降趋势。可以看出在变形过程中，最大扭转角为±90°的滞回线对应的峰值应力始终高于最大扭转角为±60°的滞回线，两者分别对应的最大扭转角虽然不同，但峰值应力变化是同步的。

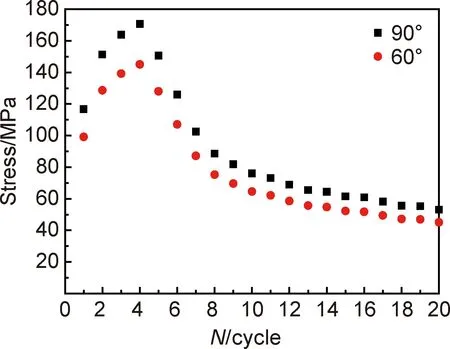
图4 扭转过程中峰值应力变化Fig.4 Variations of peak stress during torsion

2.2 织构变化

采用EBSD技术所测得镁合金挤压棒材及扭转试样的极图如图6所示，其中图6(a)所示的织构特征与图5所示的宏观织构一致，而图6(b)中的{0001}极图显示，经过单周90°扭转变形后，晶粒的C轴不再沿径向均匀分布，表明该变形过程中，晶粒取向发生明显变化，图2(a)的应力-应变滞回线的硬化特征显示，该变形过程中无大量孪晶启动，滑移系启动为该变形过程的主要微观机制，滑移系启动受到约束时也能明显改变晶粒取向[24-25]。图6(c)，(d)中的极图显示，经过多周期的循环扭转变形后，相比于原始的挤压棒材，织构特征无明显变化，扭转后的试样仍保持为晶粒C轴沿径向均匀分布的特征。

图5 镁合金挤压棒材的极图Fig.5 Pole figures of magnesium alloy extruded rods

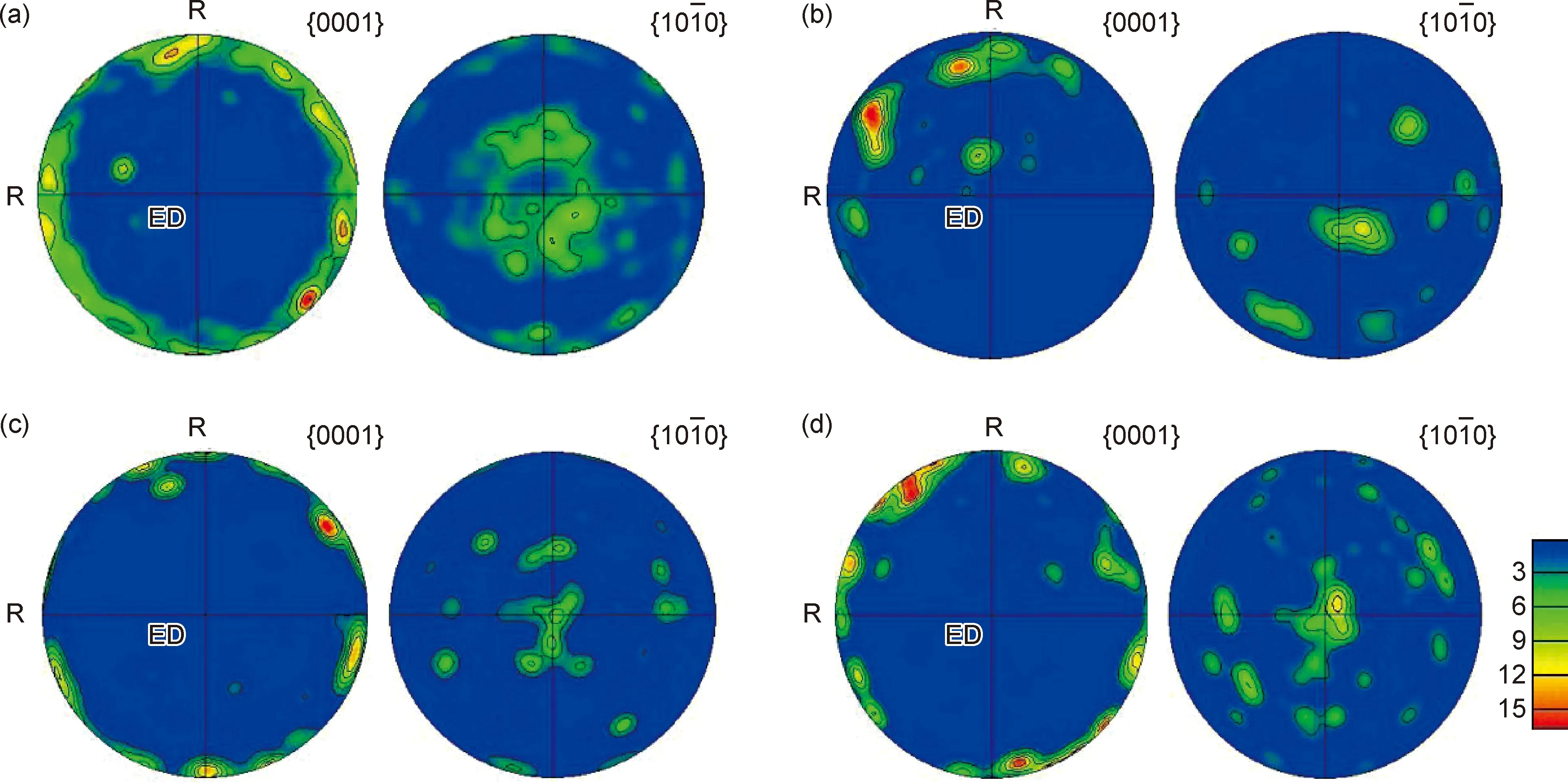
图6 挤压棒材及扭转试样EBSD所测得极图(a)挤压棒材;(b)1周±90°;(c)20周±90°;(d)20周±60°Fig.6 Pole figures of extruded rods and twisted specimens measured by EBSD(a)extruded rods;(b)±90° with one cycle;(c)±90° with twenty cycles;(d)±60° with twenty cycles

2.3 孪晶机制

图7为采用EBSD技术所测得挤压棒材及扭转试样的晶粒取向图，图7(a)显示挤压棒材微观组织由尺寸差异较大的大小晶粒组成，其中小晶粒均匀分布在大晶粒的晶界处或晶粒内部，应该为挤压过程中动态再结晶所生成，组织中无孪晶带。

图7(b)～(d)显示挤压棒材经过循环扭转变形后在晶粒内生成了孪晶带，表明在变形过程中有孪晶启动，在镁合金的各种微观变形机制中，拉伸孪晶由于其临界剪切应力(critical resolved shear stress，CRSS)值低而易启动，变形过程中大量的拉伸孪晶启动将对宏观应力应变曲线产生明显影响。

图8显示了扭转试样中的拉伸孪晶界和晶粒内的小角度晶界的分布，可以看出总循环周期数为20的扭转变形试样的孪晶界的数量要多于单周扭转试样，单个晶粒内的孪晶界多数呈现平行排列，少量孪晶界呈交叉状态。孪晶界主要分布于大晶粒内部，一些小晶粒内没有形成孪晶界，表明大晶粒在扭转变形过程中更需要孪晶启动来协调变形。

在图7(b)～(d)对应的晶粒取向图中分别选取若干孪晶带，分析孪晶带及其对应晶粒基体的取向分布特征，图9(a)，(c)，(e)显示了孪晶带所在的晶粒基体的取向分布，可以看出晶粒基体的C轴接近于与ED垂直，并沿圆周方向较均匀分布，与图5和图6所显示的挤压棒材中晶粒取向特征一致。图9(b)，(d)，(f)则显示在拉伸孪晶启动后，多数孪晶带内的晶粒取向特征为晶粒的C轴接近于与ED一致，少数孪晶带内晶粒的C轴则垂直于ED。

图7 挤压棒材及扭转试样的晶粒取向图(a)挤压棒材;(b)1周±90°;(c)20周±90°;(d)20周±60°Fig.7 Grain micrographs of extruded rods and twisted specimens(a)extruded rods;(b)±90° with one cycle;(c)±90° with twenty cycles;(d)±60° with twenty cycles

在镁合金的塑性变形过程中，拉伸孪晶的启动将使晶粒的C轴产生约86.3°的偏转，从而明显改变晶粒取向。图9中的孪晶带内晶粒的取向特征表明，循环扭转变形过程中，拉伸孪晶启动使晶粒取向发生两种变化，其一为孪晶启动后，晶粒的C轴由垂直于ED转变为平行于ED，另一种变化则为孪晶启动前后晶粒的C轴始终垂直于ED，并且以前一种变化为主，这两种晶粒取向的变化特征可用图10表示。本工作定义孪晶启动后晶粒的C轴接近平行于ED的孪晶过程为T1孪晶，而孪晶启动后晶粒的C轴仍垂直于ED的孪晶过程则为T2孪晶，图10中显示T1孪晶启动使晶粒的C轴由垂直于ED转变为平行于ED，而T2孪晶使晶粒的C轴在垂直于ED的平面内产生86.3°的偏转。

在图9(b)，(d)，(f)中，将孪晶带内晶粒的C轴取向位于小圆(半径为大圆的一半)内的孪晶划归为T1孪晶，将小圆外的孪晶则划归为T2孪晶，由图9所示结果可以看出，绝大多数晶粒内的孪晶为T1孪晶。基于拉伸孪晶启动应满足的载荷条件，对于具有基面织构的镁合金棒材，当沿棒材的轴向进行压缩变形时，T1孪晶易启动[26-27]。上述孪晶取向特征分析结果表明，对于无轴向约束的镁合金棒材的循环扭转变形，孪晶启动的取向特征与棒材的轴向压缩相近。

图10 孪晶引起晶粒取向变化的示意图Fig.10 Schematic diagram of grain orientation variation caused by twinning

镁合金棒材单向扭转过程的孪晶启动机制分析表明[28]，当扭转变形的试样表面切应变大于5%时，在靠近试样表面的边缘处有拉伸孪晶启动，拉伸孪晶启动使晶粒的C轴由垂直于ED转变为与ED成约60°的夹角。图9中的孪晶取向特征表明，孪晶的C轴主要位于与ED成45°夹角的范围内。上述拉伸孪晶的启动是由垂直于晶粒的C轴的压应力引起的，如图11所示，在棒材的扭转变形过程中，在扭矩M作用下的试样的表面受到与ED和径向成45°角的主压应力作用[28]，该压应力沿ED方向产生压缩，也就是产生垂直于晶粒的C轴的压应力，从而满足拉伸孪晶的启动条件，拉伸孪晶启动后使晶粒的C轴向ED偏转。

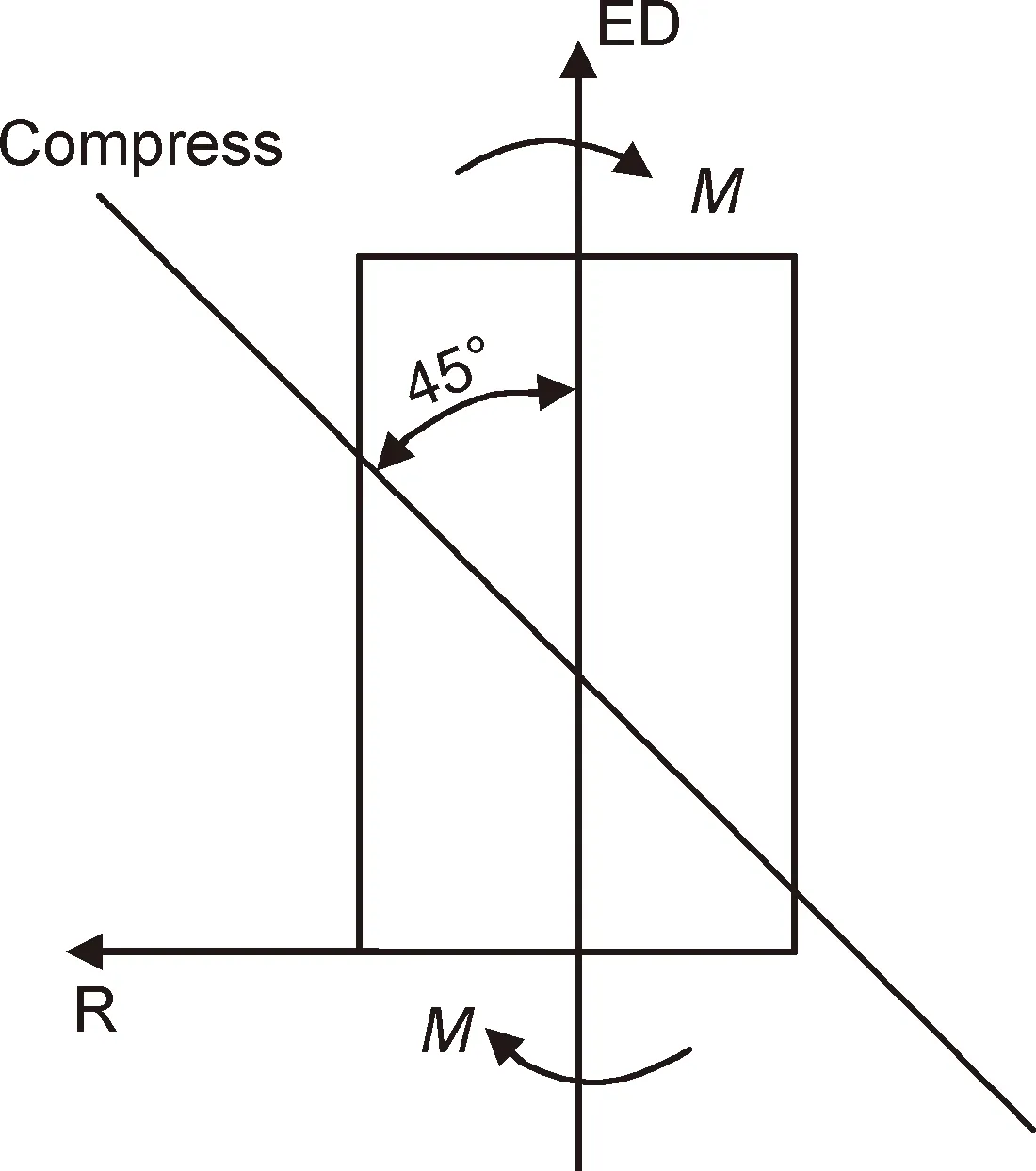
图11 棒材扭转过程受力示意图Fig.11 Schematic diagram of loading on the twisted rod

虽然图7和图8显示在晶粒内启动了较多孪晶，但图6中的扭转变形后的织构特征表明，与原始棒材的织构特征相同，试样在扭转变形后仍保持为基面平行于轴向的基面织构，这是因为孪晶带的体积还是远小于晶粒基体的体积。虽然孪晶启动没有对试样的织构特征产生明显影响，但变形后期的滞回线硬化特征已经表明，孪晶启动对宏观力学性能曲线产生了明显的影响。

2.4 扭转后的压缩变形

图12为镁合金棒材在扭转前后沿轴向压缩时的应力-应变曲线，图中曲线都为典型拉伸孪晶启动的S型曲线，镁合金棒材扭转变形前后的织构特征表明，当棒材沿轴向压缩变形时，应力方向与晶粒的C轴垂直，符合拉伸孪晶启动条件，从而引起CRSS值较低的拉伸孪晶在变形初期大量启动，使应力-应变曲线呈现低屈服点，在变形后期则为CRSS值较高的柱面或锥面滑移系启动，曲线则呈现快速硬化特征。

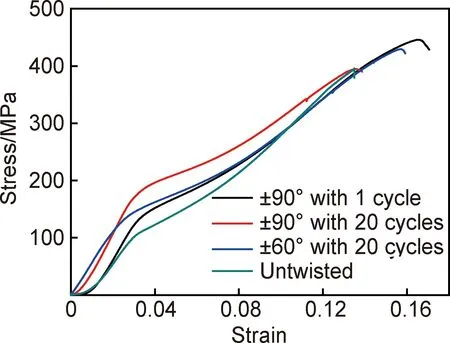
图12 镁合金棒材扭转前后压缩变形的应力-应变曲线Fig.12 Stress-strain curves of magnesium alloy rods before and after twisting

图12中显示未扭转的镁合金棒材的应力-应变曲线对应的屈服强度最低，约为100MPa，扭转变形后对应的屈服强度都有所提高，最大提高至约200MPa，这是因为扭转变形提高了镁合金棒材晶粒中的位错密度，增加了孪晶启动过程中不完全位错运动的阻力，从而导致宏观屈服强度增加。图12中的扭转周期分别为20周和1周，最大扭转角都为±90°的应力-应变曲线对比表明，在相同的最大扭转角条件下，循环扭转次数的增加将提高镁合金棒材的强度值。图8(a)，(b)中的小角度晶界分布情况对比表明，20周试样内的小角度晶界的数量要远高于1周试样，由于小角度晶界的分布可以表示位错密度分布情况[28]，则意味着在最大扭转角都为90°条件下，扭转20周所产生的位错密度要远高于扭转1周，从而使前者在扭转后的压缩屈服强度远高于后者。

图12中的曲线对比也表明，在循环扭转周期数都为20的条件下，最大扭转角为±90°的曲线的强度值明显高于最大扭转角为±60°的曲线，表明扭转角的增大将增加棒材压缩变形的强度值。镁合金棒材的单向扭转的相关研究表明[13]，扭转变形后的压缩屈服强度随扭转角的增大而增大。公式(2)表明，扭转产生的切应变量与扭转角成正比，扭转角的增大使应变量增大，从而增加了位错密度。图8(b)，(c)中的小角度晶界分布情况对比表明，在扭转周期数都为20的条件下，最大扭转角为±90°试样内的位错密度要远高于±60°试样，从而导致前者的扭转后压缩屈服强度明显高于后者。