灵活化归探析圆锥曲线中的距离问题
2019-09-19董顶国
董顶国
(上海市松江一中 201600)
圆锥曲线中距离问题是高考的热点内容.通常使用距离或弦长公式转化求解,但也有较多的距离问题使用此法,要么难以解出、要么过于繁琐.为了准确选择解题思路 , 快速解决此类问题,本文对距离常见转化作如下辨析.
一、利用两点间的距离公式或弦长公式结合曲线性质建模求解

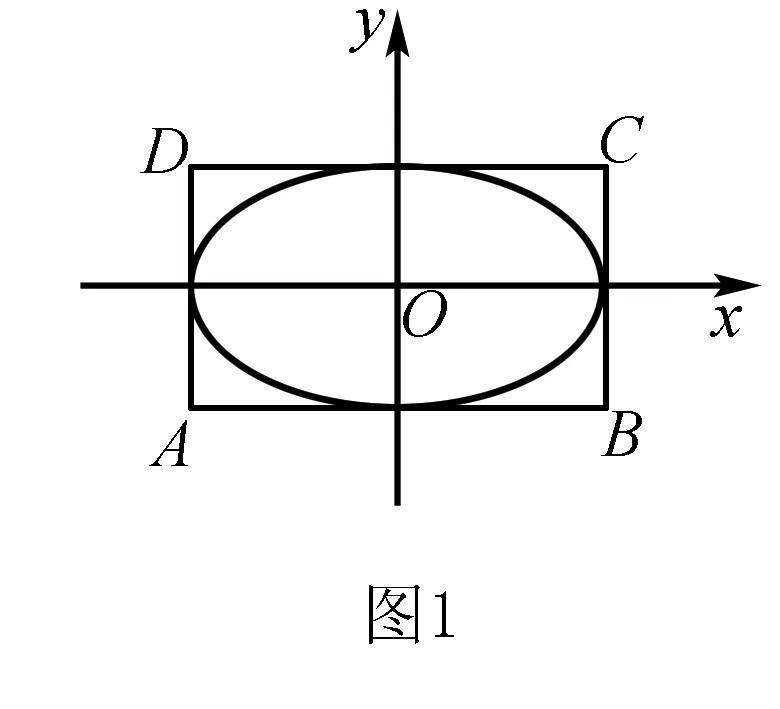
(1)求椭圆M的标准方程;
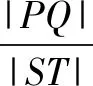
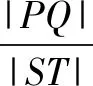
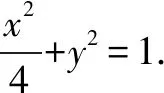
(2){x2+4y2=4,


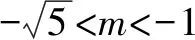
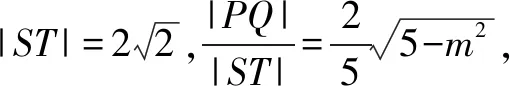
点评该问题中距离处理运用公式常规转化,但对|ST|的求解要结合图形分类求解,较多的考题也结合曲线性质和定义直接求解.
二、运用射影思想降维转化求解
将有关的线段投影到坐标轴上,化二维空间的问题为一维空间的问题,结合曲线方程达到求解的目的.
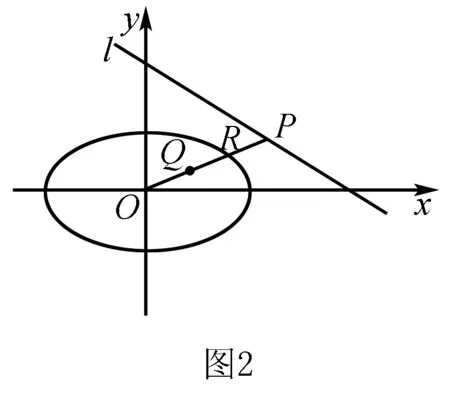
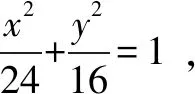
解析问题关键是对|OQ|·|OP|=|OR|2处理,把关系|OQ|·|OP|=|OR|2投影到x轴上降维求解.
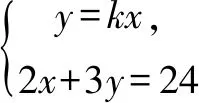
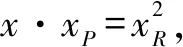
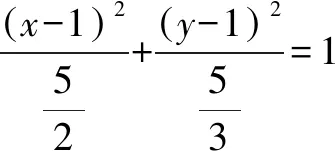
点评本题主要考查直线、椭圆的方程和性质,轨迹方程求法.求解问题的关键是合理降维.
三、借助曲线定义结合性质求解
圆锥曲线的第一定义和第二定义都与距离有关,利用这两个定义可以把两个动距离的和、差、商转化为定值, 结合性质解决问题.


解题分析(|PM|-|PN|)max=|PM|max-|PN|min.
设圆(x+5)2+y2=4的圆心为F1(-5,0).
设圆(x-5)2+y2=1的圆心为F2(5,0),|PM|max=|PF1|+2,|PN|min=|PF2|-1.
所以(|PM|-|PN|)max=|PM|max-|PN|min=|PF1|+2-(|PF2|-1)=(|PF1|-|PF2|)+3=9
点评该类问题的核心是利用圆的几何性质和双曲线定义,把两动点距离化归为动点到圆心的距离问题,减少了变量个数,简化了思考过程.
四、距离关系转换为向量关系求解
向量的模就是向量起点和终点间的距离 , 因而圆锥曲线中的距离问题即可转化为平面向量的模的问题,化距离关系为向量关系,进而转化为向量的坐标来解决.
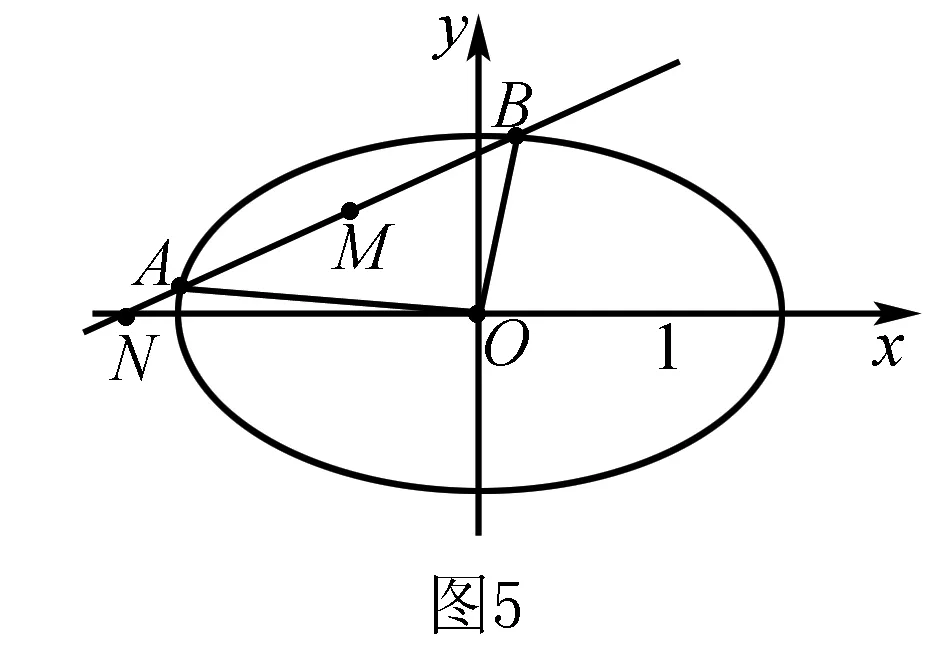
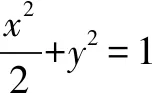


设直线l的方程为y=k(x+2),代入椭圆方程得:(1+2k2)x2+8k2x+8k2-2=0.


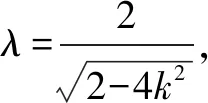
点评将长度关系向量化后,再将向量关系坐标化时往往会遇到纵、横坐标的选取,选择的原则是以简便为主.
五、中点公式法求解距离相等问题
对于直线与两种曲线相交所截得线段长相等问题,用中点坐标公式解决可收到事半功倍之效.

例5已知抛物线y2=x和圆(x-7)2+y2=5,过点P(a,0)作直线l交抛物线于A,B,交圆于C,D,(自下而上依次为B,D,C,A),且|AC|=|BD|,求a得取值范围.
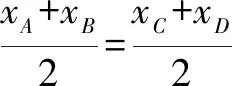

当直线l的斜率存在设为k(k≠0),方程为y=k(x-a).
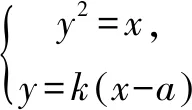
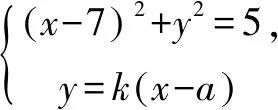
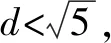
∵|AC|=|BD|,
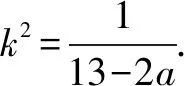
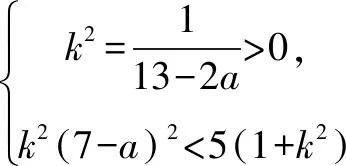
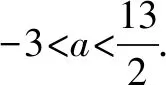

点评若|AC|=|BD|,则AB,CD的中点重合,反之也成立.由四点共线,等价转化为两中点横坐标的相等.这一转化充分利用了曲线的几何性质,大大简化了解题过程.
