基于松组合的视觉惯性SLAM方法
2019-09-19
(东南大学 仪器科学与工程学院,江苏 南京 210096)
单目视觉SLAM算法是机器人自主导航、增强现实跟踪注册等领域的研究热点。SLAM的本质是贝叶斯状态估计,依据观测方程不断更新状态方程[1]。传统的SLAM算法在环境中缺乏标志物或者环境单一的情况下会出现定位不准确的问题。基于此问题研究了视觉惯性SLAM算法[2]。通过在前端提取特征点,进行特征点匹配建立地图,同时在后端通过非线性优化算法来求解。该组合方法一方面,相机提供了丰富的环境信息,可以构建三维模型、定位和识别相机已经访问过的地点;另一方面,SINS传感器提供了自运动信息,可以恢复单目视觉的尺度信息、估计重力方向、提供可视的绝对俯仰和滚动[3]。但上述方法还存在以下问题:① 没有回环检测或缺乏地图重利用功能,这会导致预测的轨迹漂移不断增加;② 紧耦合的视觉惯性系统考虑了特征之间的交叉耦合使其运算复杂度为O(M2),这制约了紧耦合系统的工作范围,当SLAM的地图扩展到一定大小,实时性就很难被满足;③ 传统的SLAM/SINS组合导航系统中SINS的价格比较昂贵,无法满足一些特定使用场合[4]。
针对上述问题,首先提出了一种在移动设备上实现的视觉惯性SLAM松组合组合方法,降低计算复杂度;通过使用移动设备自带的消费级陀螺仪满足了特定场合的定位精度,如移动端增强现实的跟踪注册。其次,对关键帧进行回环检测,提高了定位精度,解决了漂移问题。
本文研究单目视觉ORB-SLAM/SINS松组合的定位技术。介绍了传统视觉惯性SLAM方法的不足;基于ORB-SLAM算法的工作原理,根据ORB-SLAM的输出,结合SINS导航并利用最小二乘法计算出尺度因子;同时,构建SLAM/SINS的非线性卡尔曼滤波器,将ORB-SLAM系统输出的姿态信息经过尺度变换后作为卡尔曼滤波器的观测量;最后通过3个实验来验证本文算法的可行性。
1 整体框架
系统主要包括3个部分。首先通过ORB-SLAM算法求出相机的相对姿态和位置;然后结合SINS导航求得ORB-SLAM算法的尺度因子;最后将ORB-SLAM算法的输出经过尺度因子的变换后作为观测量进行卡尔曼滤波,从而实现视觉惯性SLAM定位松组合方法。算法的整体框架如图1所示。

图1 视觉惯性组合方法整体框架
2 单目ORB-SLAM算法及尺度因子估计
2.1 单目ORB-SLAM算法
单目视觉ORB-SLAM算法分为3个并行的线程[5]:跟踪、地图构建以及回环检测。算法的总体框架如图2所示。

图2 ORB-SLAM算法总体框图
追踪模块首先从图像中提取ORB[6]特征点,然后进行姿态估计,利用邻近的地图点,寻找更多的能成功匹配的特征点以实现姿态优化,最后选取关键帧完成地图构建的初始化。
地图构建模块通过不断地插入关键帧并对其中的特征点进行极线搜索匹配。利用三角法生成新的地图点并使用局部光束平差法对不符合要求的地图点去除局外点和重复帧。最后插入新的地图点,再利用光束法平差对其进行优化,从而实现对局部和全局地图的更新。
回环检测模块包括回环探测和回环校正,其中,回环检测通过Bag of Words(BOW)算法[7]实现,即首先匹配每个候选的回环帧和当前帧上的特征点,然后用得到的特征点所对应的三维点求解RANSAC的相似变换矩阵。回环校正通过对回环检测的结果进行优化,从而提高单目ORB-SLAM算法的稳定性。
2.1 尺度因子估计
由于单目视觉本身不具有深度信息, 尺度因子无法确定,因此尺度因子的估计问题是单目视觉ORB-SLAM/SINS组合导航系统首要解决的问题。
在传统的采用人工标记的单目视觉SLAM技术中,常用到以下4个坐标系:图像像素坐标系、理想屏幕(成像平面)坐标系、摄像头坐标系以及世界坐标系。类似地,在所采用的单目视觉SLAM技术中,使用如下4个坐标系:图像像素坐标系、成像平面坐标系、相机坐标系以及世界坐标系。其中,视觉坐标系(V系)的Z轴与初始化的平面垂直;相机坐标系(C系)的原点为相机的镜头光心,坐标系Z轴与成像平面垂直,摄影方向为坐标系的正向,C系的X、Y轴分别与图像坐标系对应轴平行。在此基础上,将输出结果与SINS的输出结果进行融合,故而在组合系统里,关于视觉系统,主要研究V系与C系。视觉系统参考坐标系如图3所示[8]
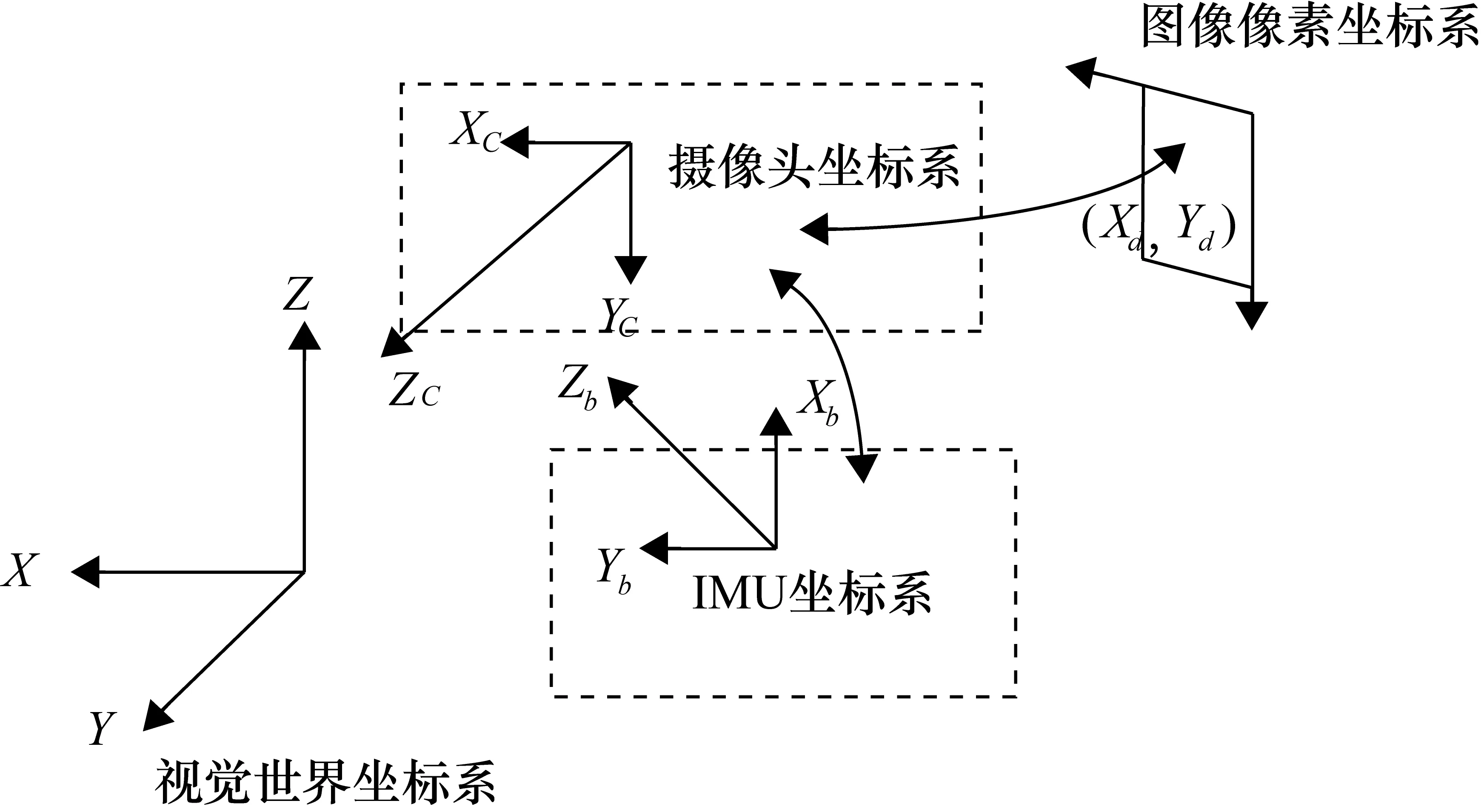
图3 视觉系统参考坐标系
(1)
(2)
式中,s为未知的尺度因子。

(3)
(4)

(5)
(6)
(7)
根据式(5)~式(7)可以计算出线性加速度和角速度。

(8)
综上所述,通过将SLAM与SINS结合估算单目SLAM的尺度因子,从而在得到尺度因子之后将ORB-SLAM系统输出的位置信息经过尺度变换后作为观测量进行卡尔曼滤波更新。
3 ORB-SLAM/SINS组合滤波器设计
为了准确表示SINS测量数据的误差,对于陀螺与加速度计的测量值,采用的惯性传感器模型如下:
(9)
该模型假设SINS的输出ωb(角速度)与ab(加速度)包含静态偏差b以及动态偏差n,动态偏差被视为高斯白噪声,ω与a为真值。
另外b的变化是一个高斯随机过程:
(10)
3.1 系统状态方程
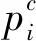
(11)
状态方程的差分形式为
(12)
(13)
(14)
(15)
式中,g为导航坐标系下的重力加速度向量;Ω为角速度ω的四元数乘积矩阵。
3.2 系统误差方程
当姿态误差较小的时候,为了增加数值稳定性采用四元数来表示误差。此时的四元数为其最小表达形式,根据文献[10]可得:
(16)

(17)
(18)

据此,系统的误差状态向量为
(19)
误差状态方程的差分形式为
(20)
(21)
(22)

(23)
通过四阶龙格库塔方法离散化系统的误差状态方程,并且根据SINS采集的数据,持续更新系统误差状态。
3.3 系统量测方程
(24)
(25)
其误差量测方程由文献[12]求得
(26)
(27)
扩展卡尔曼滤波器可以通过每次获得视觉系统的更新,计算出卡尔曼增益K,而后更新协方差P,并且利用ORB-SLAM系统的输出修正惯性系统的预测值从而达到预期效果。
4 实验验证与分析
4.1 实验平台搭建
考虑到设备的稳定性和平衡性,采用iPhone作为实验平台。并在Ubuntu 16.04的操作系统下利用标准数据集进行算法验证,系统实现为能够在iPhone设备上实时运行的iOS程序。使用手机捕获的频率为30 Hz,分辨率为640像素×480像素的图像,以及内置InvenSense MP67B 六轴陀螺仪和加速度计获得的100 Hz的IMU数据。
4.2 实验结果演示与分析
4.2.1 定位对比实验结果
采用TUM标准的数据集比较了ORB-SLAM和ORB-SLAM/SINS组合方法在X,Y,Z轴方向上的定位精度,实验结果如图4所示。所提出的ORB-SLAM/SINS的定位结果与标定好的真实数据几乎重合,由此可见本文提出的ORB-SLAM/SINS组合导航方法较之前的定位算法的精度有了比较好的提升,因此采用的方法是可取的。
4.2.2 EuRoC标准数据集实验
本次实验分为两个部分,第一部分利用EuRoC标准数据集中的单一序列(MH_01_EASY)来验证本文算法的可行性,实验结果如图5所示(取极短时间),轨迹①代表的是标定好的真实数据,轨迹②表示的是利用本课题的算法预测的轨迹,实验结果表明,真实的轨迹与预测出的轨迹基本一致。第二部分融合数据集中的3个序列(MH_01_EASY、MH_02_EASY、MH_03_MEDIUM)对回环检测进行验证,这3个序列中包含旋转和光照变化。实验结果如图6所示,其中,轨迹①代表的是标定好的真实数据,轨迹②表示的是利用本课题的算法预测的轨迹,而轨迹③则表示融合了3个序列的场景之后本文算法在运行的过程中会进行回环检测。

图4 定位误差比较

图5 MH_01_EASY 运行结果
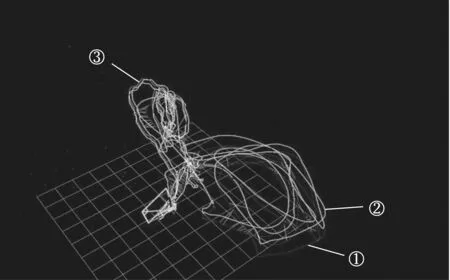
图6 融合数据回环检测实验
4.2.3 移动增强现实实验
在本实验中,将本文的组合系统输入到一个移动设备,使用AR应用程序演示系统对实时漂移消除的能力。在图7实验中,将一个虚拟立方体插入到利用SLAM/SINS估计的视觉特征提取的平面上,手持手机以正常的速度在房间里走动,由于增加了回环检测模块,立方体在经过位移后可以注册到图像上的同一个位置,即可证明累积的漂移可以得到有效地消除。

图7 漂移消除能力
5 结束语
本文把单目视觉ORB-SLAM与SINS相结合,利用智能手机内置的消费级陀螺仪研究了一种基于松组合的视觉惯性SLAM组合方法。根据惯导与视觉在时间与空间上的互补关系,实现了融合惯导与视觉数据的非线性卡尔曼滤波器。增加回环检测功能使得系统具有较好的漂移消除能力。设计实验平台,采用标准的数据集对本文提出的算法与开源的SLAM算法进行比较,验证算法的正确性,另外,在智能手机上开发增强现实软件,通过增强现实对跟踪结果进行演示,验证在较大的空间范围和环境干扰下,具备较好的漂移消除能力。在SLAM未来的研究方向上计划在地图创建上采用深度学习等方法建立语义地图。
