改进型分批估计与自适应加权融合方法研究
2019-09-20
(1.福建师范大学福清分校 图书馆,福建 福清 350300; 2.福建师范大学福清分校 电子与信息工程学院,福建 福清 350300)
目前,无线传感网络在智能家居中的应用越来越广泛。而无线传感网络数据量测的准确性和可靠性是其正确应用的基础。然而它依然存在着一些待解决的问题[1-2]。首先,在智能家居中,大量的传感器节点部署于相对较小且半封闭式的空间内,进行数据收集、存储处理、无线传输等。在该监测区域内,区域温度和压力变化较大,易受电器辐射和噪声干扰,使得传感器采集数据读数不准确,终端节点与协调器的无线数据传输不稳定、易丢失等,最终导致收集到不正确的数据。此外,在某些情况下,节点本身出现故障瘫痪,发出错误数据或成员节点直接失效,收集不到数据。其次,无线传感网络是自组织网络,节点受空间覆盖,时间校准的问题导致收集不正确的数据时有发生,特别是障碍较多的室内环境,信号覆盖范围受障碍影响大,易造成信号衰弱,影响数据可靠性。第三,小区域内的传感器监测,空间位置相邻,容易产生高度重复的相关性数据,该局部监测区域的大量数据传输显得多余,占据了信道带宽,浪费信道利用率,降低服务质量。第四,智能家居的某些应用中,用户可能更关心的是监测结果,而原始数据的状态并不那么重要[3],例如发生火灾能够迅速警报等。基于这种情况,仍然将各个节点的原始监测数据传输至协调器以及Sink节点,无法获得更有用的信息,代价是传输大量数据,反而有可能因为信道竞争导致预警延迟。
为了解决上述问题,对多源传感器数据进行预处理及有效的数据融合机制,修正偏差大的数据,删除不可靠数据,去除冗余、融合高度重复的相关数据,是实现提高数据可靠性、精确性、降低冗余度的有效途径之一。针对监测环境局部信息的一致性和变化缓慢的特点,文献[4]提出了层次数据融合结构;对局部区域内采用加权数据融合状态估计,然后基于支持度函数对来自不同局部区域内数据进行一致性分析,确保了信息的一致性和有效性。文献[5]提出了一种基于三层架构的上下文感知、自我优化和自适应系统;最低层传感器收集异构数据,中间层结合上下文信息利用动态贝叶斯原理处理测量数据的不准确性并推理估计,最高层通过采集传感器集数据实现自由优化过程达到提高监测值的精度;结合卡尔曼滤波的优化贝叶斯估计也被用于改善多传感器数据的不确定性和不一致性问题[6]。为了提高多传感器测量的准确性,文献[7]提出了一种基于偏好聚合形式的区间投票的方法;允许从狭窄的不确定性边界内相邻多传感器获得不准确的测量数据来确定测量参数的校正值,实现较好的测量准确度。针对各种传感网络模型中存在的错误、无用及冗余数据进行优化,引入模糊推理系统进行数据融合提高精确性和融合质量[8-9]。文献[10]采用支持向量回归机方法将各传感器阵列数据进行融合以提高数据的准确性。文献[11]提出了一种改进型分批估计的自适应加权融合算法,根据容许函数阈值剔除误差较大的数据,利用改进型分批估计最优估计值,依据权值最优分配原则对每组传感器数据进行组内自适应加权融合,从而计算精确值。本文在借鉴分批估计算法的基础上,考虑受到环境因素影响造成监测偏差程度,提出了一种数据预处理与改进型分批估计加权融合相结合的算法。首先,该算法根据格罗贝斯准则一致性检验剔除疏失误差数据;其次,引入环境因子改进分批估计算法计算当前最优监测值;最后,针对不同方位误差分布不均匀特点,提出了权值最优分配原则实现自适应加权融合。
1 量测数据融合模型
无线传感网络终端节点数据采集完成后得到原始测量序列Xi={xi1,xi2,…,xik},k为每个传感器周期内测量次数。量测数据融合过程如图1所示。
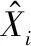
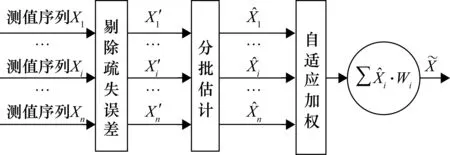
图1 量测数据融合模型
2 量测数据预处理
实际测量中,必然存在着疏失误差。智能家居安全监测中,利用带有疏失误差的量测结果判别预警结果是可靠的。因此,对于误差偏大、错误的量测数据应该及时予以剔除,从而拒绝因疏失误差而导致误判的情况。采用格罗贝斯判据准则[12-13]进行数据一致性的检验。具体方法描述如下。
设某一传感器节点i,某一采集周期内多次测量得到的量测序列为:Xi={xi1,xi2,…,xik}。其中,k为每个传感器周期内测量次数。同时,设该原始数据服从正态分布,计算可得
(1)
(2)
(3)
根据顺序统计原理,可知格罗贝斯统计量的确切分布。在给定显著水平α后,通常取值为α=0.05或α=0.01,通过查表法找出格罗贝斯统计量的临界值gi(k,α)。因此,由量测数据序列Xi服从正态分布,可知:
(4)
P[gij≥gi(k,α)]=α
(5)
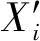
3 改进型分批估计融合算法
完成了对疏失数据的剔除工作,得到具有一致性的量测数据序列。针对单传感器的一致性量测序列,它们之间必然有着关联性,具备高度重复性,这是其一。其二,对于单点传感器以及整个系统而言,只需获取一个监测结果。因此,对具有一致性量测数据序列进行监测值融合估计,高效地反映当前传感器的状态是很有必要的。对此,分批估计融合是一种简单可靠的可行方案。但在实际测量使用过程中,传感器测量受到复杂环境因素影响多变,可能存在均方差偏大的一致性检验数据,特别是与电子设备本身的电气特性,以及不同方位受实时坏境,如轻微震动、受潮等诸多不可预期的因素有一定关系,因此通过引入环境因子来克服由此造成的误差,即根据检测区域环境的特点,选择性地去除一定比例的最大最小值,有利于提高精确度,而传统分批估计采用简单算术均值计算在该方面具有一定的局限性。对此,依据顺序统计理论和实践经验,去除部分最大最小值后的均值分析,显得更加可靠和准确,更能够反映数据的集中情况。
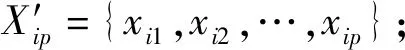
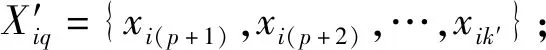
其中,两组元素个数分别为p和q,且满足p+q=k′。分别计算各组的算术平均值和方差,如下:
(6)
(7)
(8)
(9)
式中,ρ表示环境因子,指最优去除最大最小百分比。
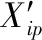
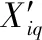
故此,根据文献[2],利用分批估计理论可以求出该组传感器量测数据序列最优融合监测估计值为
(10)
分批估计数据融合监测值的方差为
(11)
至此,考虑传感器受恶劣因素影响导致量测值波动较大,通过引入环境因子ρ,对单个传感器经一致性检验后的测量数据序列进行分批估计,给出了最优融合监测值及总方差。
4 自适应加权融合算法
尽管对于单传感器数据测量准确性和可靠性提出了解决方案,然而,往往在局部区域内部署着多个同类型的传感器节点,每个节点因方位、环境、噪声干扰不同,感测值是不一样的。因此,每个传感器量测数据的准确性存在差异,量测误差随机性大,分布不均匀。那么,如何有效区别对待各个传感器的数据差异,提高数据融合监测结果的可信度,是必然要解决的问题。本文采用权值最优分配原则,自适应加权融合,为每个传感器数据自适应寻找其最优权值,使得总均方误差最小,从而得到该监测目标的最优估计值[14-16]。自适应加权融合计算模型如图2所示。
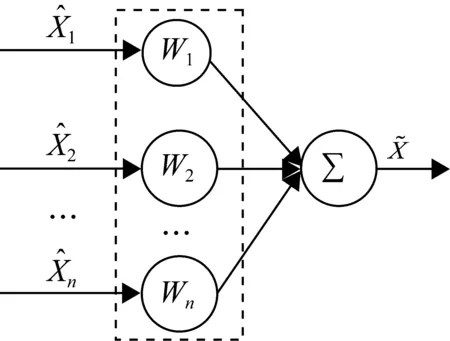
图2 自适应加权融合计算模型

(12)
融合后的总均方差为
(13)
(14)
通过自适应权值分配,即可使得量测方差越大,获得权值越低,否则相反。
5 实验结果与分析
在火灾监测状态正常情况下,室内环境传感器数据采集受环境因素干扰小且可能性较低,数据测量表现较为稳定;若有火情发生或处于萌芽阶段,室内环境监测区域环境变化迅速多样且复杂,对传感器自身及其测量产生不利影响,造成测量数据偏差相对较大。为此,提出了一种数据预处理与基于环境因子的改进型分批估计相结合的方法。与此同时,该环境下,不同方位受影响程度不同,呈现出测量数据分布不均匀等特点,本文提出了综合评价多传感器测量数据,自适应加权融合方法,使得测量方差越大,获得权值越低。
5.1 算法时间复杂度分析
本文利用一致性检验方法剔除异常数据,计算均值方差求临界值及误差比较均为单层循环,故一致性检验方法时间复杂度约为O(k)。通过分批估计融合算法求单传感器最优监测值的主要计算为分组排序和求均值方差,排序方法采用两层嵌套循环,时间复杂度为O(k2)。自适应加权融合算法的主要操作为计算n个传感器的权值,为单层循环,时间复杂度为O(n)。一般地,n< 为了验证所提改进算法的有效性,通过模拟数据进行仿真分析。表1为以52 ℃为基值的40个监测数据样本,并设环境噪声等因素干扰为10%以内,另外设置一定比例的异常值。为了说明方便,不妨设序列为X1={x11,x12,…,x1j,…,x1(40)}。 表1 室内温度监测数据样本 5.2.1 数据预处理结果分析 通过对表1数据进行计算,可得均方差: 对于序列X1存在:|ε11|=4.48>3.80768。 所以x11=46.91为可疑值,判定为疏失误差数据,应予以剔除。剔除完成之后,该组均余下39个数据。经验证,对于所有X1j(2≤j≤40),均满足g1j 5.2.2 改进性分批估计结果分析 表2 改进型分批估计融合结果 可分别计算改进前和改进后的监测估计值: 由此可见,改进型分批估计方法估计得到的估计监测值更接近真实值。需要说明的是,分批数可根据传感器数据监测次数大小而设定,若所获得监测数据较多时,分批次数越多,方差越小,优点更明显;若所获得监测数据较少时,分批次适当减少,可获得更好的实时性。同时,当数据量较多时,可根据实际设定ρ的取值。针对不同的ρ的取值进行计算分析,如图3所示。可知,随着ρ值的递增,估计值尽管变化微小,但总体趋势是更接近于真实值的。当ρ达到一定的比例值时,估计值趋于稳定。故依据顺序统计理论和实践经验,可适当地去除部分最大最小值后分批估计,具有更好的可靠性和准确性,更能够反映数据的集中情况。 图3 ρ-估计值变化曲线图 5.2.3 自适应加权融合结果分析 采用上述方法,监测并统计监测区域内5个不同方位传感器的数据,进行加权融合,结果如表3所示。 表3 自适应加权数据融合结果 智能家居安全是人类进行生产活动的重要保障。数据监测的准确性和可靠性是实现安全火灾监测准确预警的关键基础。数据融合是去除冗余、错误和置信度差的数据的有效方法之一。对多源传感器数据进行预处理及有效的数据融合机制,修正偏差大的数据,删除不可靠数据,去除冗余,融合高度重复的相关数据,是实现提高数据可靠性、精确性的有效途径之一。为此,本文提出了一种数据预处理与改进型分批估计加权融合相结合的算法。首先,该算法根据格罗贝斯准则一致性检验剔除疏失误差数据;其次,引入环境因子改进分批估计算法计算当前最优监测值;最后,针对不同方位误差分布不均匀特点,提出了权值最优分配原则实现自适应加权融合。实验结果表明,该算法得到的融合结果误差小,能够有效提高数据准确性,降低冗余量,稳定性能好。5.2 火灾监测实验数据分析
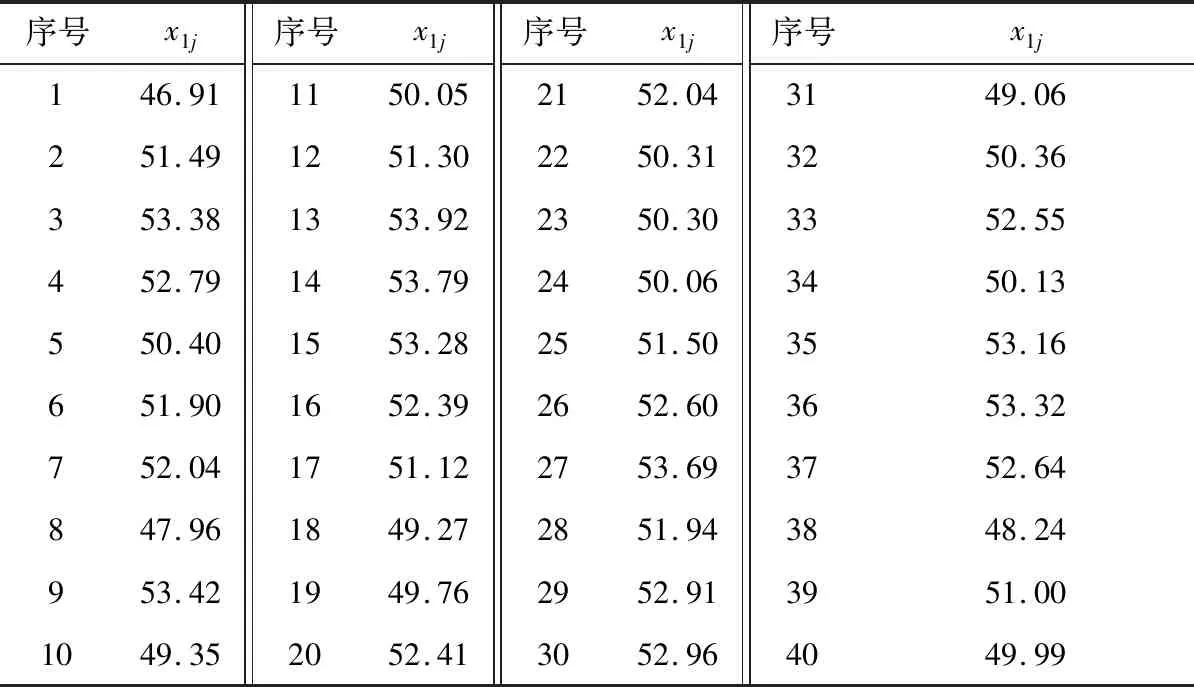
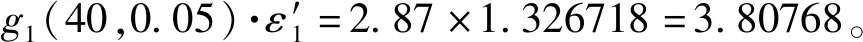

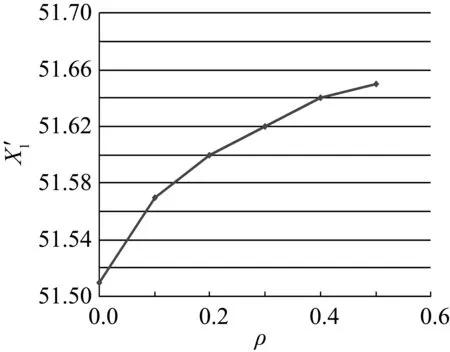
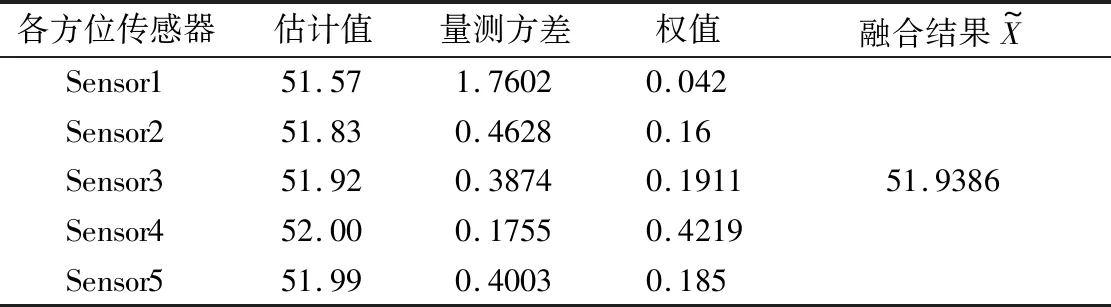
6 结束语
