轮径差对机车安全性能的影响分析
2019-09-19严松,姜毅,王欢
严 松,姜 毅,王 欢
(1.北京理工大学 宇航学院, 北京 100081; 2.廊坊师范学院 生命科学学院, 河北 廊坊 065000)
由于加工误差和实际运行环境等因素的影响,铁道车辆的车轮总存在相应的误差。如果车辆转向架的轮对存在轮径差,在运行过程中轮对就会偏离轨道中心线,产生车轮的偏磨,进而影响铁道车辆的稳定性和安全性[1]。针对轮径差,国内外的许多学者做了大量的研究。文献[1-3]定义了轮径差的基本概念,指出了轮径差的各种形式;文献[4-7]阐述了影响轮径差的各种因素;文献[8]建立了某地铁车辆模型,仿真分析了不同轮径差对车辆非线性临界速度的影响;文献[9-10]建立了某机车动力学模型,仿真分析了不同轮径差对动态曲线和小半径曲线通过的影响规律。本文以某机车为研究对象,针对轮径差的存在对机车的安全性影响进行仿真分析,研究4种典型轮径差对机车安全性能的影响。
1 轮径差及机车安全性调研分析
1.1 轮径差调研分析
轮径差是指在同一机车中,各轮对车轮滚动圆直径的差值[1]。影响轮径差的因素很多,如车轮的初期加工情况、路面不平顺、钢轨接头处的轮轨冲击、一系弹簧的许用切应力、轴重转移等,这些因素导致轮径差的表现形式有很多。虽然轮径差种类繁多,但都可以通过典型的4种轮径差组合得到[2]。如图1所示:图1(a)为标准轮径,轮对之间没有轮径差;图1(b)为等值同相轮径差,即转向架前后轮对同侧车轮直径相同,前后轮对的轮径差的大小相等且正负号相同;图1(c)为等值反相轮径差,即转向架对角线上两车轮直径相同,前后轮对轮径差的大小相等且正负号相反;图1(d)为前轮对轮径差,即轮径差仅存在于转向架的前轮对中;图1(e)为后轮对轮径差,即轮径差仅存在于转向架的后轮对中。
文献[4]指出,我国内燃机车的轮径差在机车中修规程中的规定是到辅修时,同一转向架内部的轮径差最大不能超过5 mm,同一机车内的最大轮径差不能超过10 mm。
文献[8]建立了某地铁车辆动力学模型,研究了车辆非线性临界速度随轮径差位置以及轮径差数值变化的影响规律。结果表明,不同轮径差状态下,车辆的非线性临界速度变化不同,但变化趋势相同。
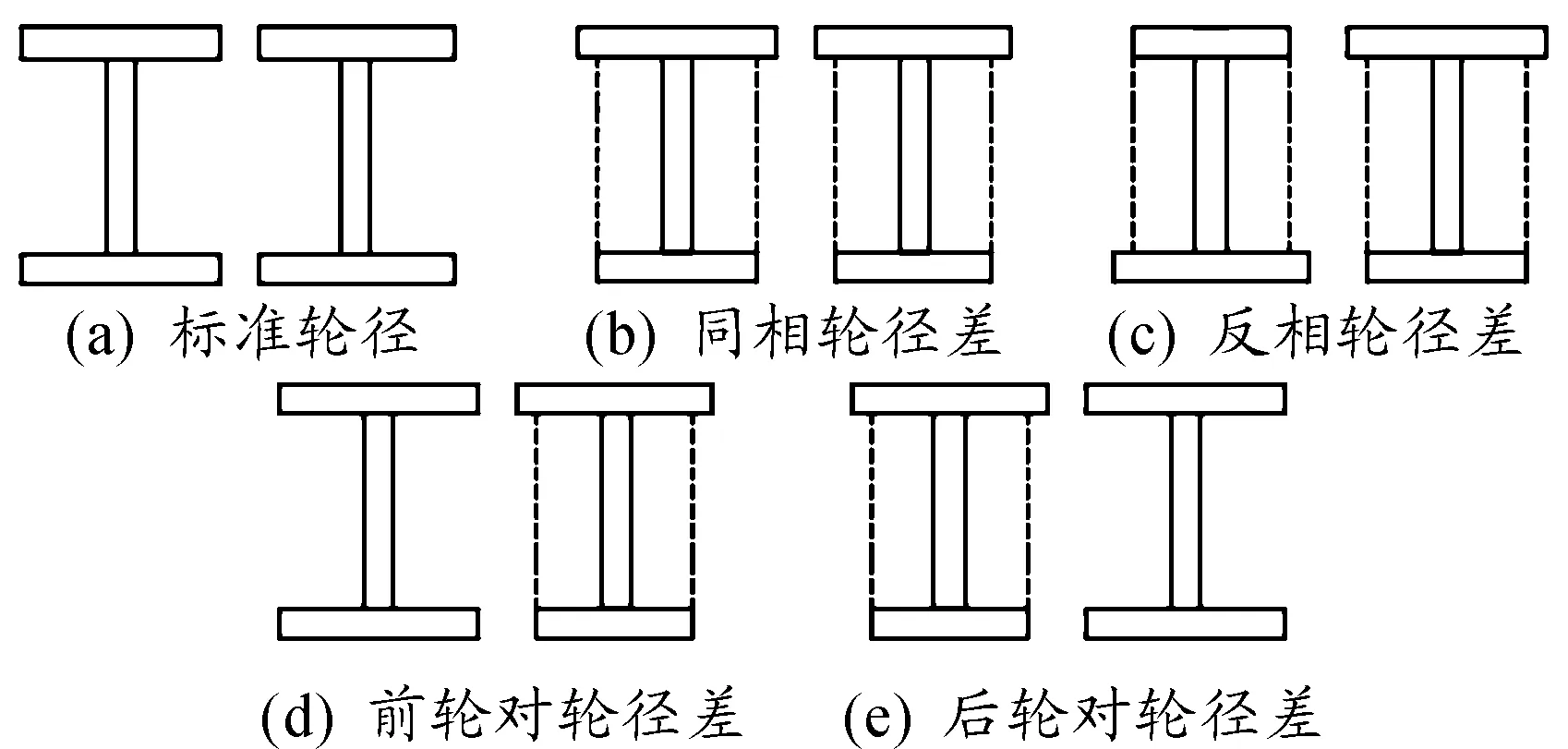
图1 转向架轮径差
1.2 机车安全性调研分析
评价机车行驶安全性的指标很多,主要有脱轨系数、轮对横移量和轮轨横向力等。
1.2.1脱轨系数
脱轨系数指的是任意瞬时车轮所受横向力和垂向力的比值。脱轨系数可由以下两个公式计算得出:
Psinα-Qcosα=μN
(1)
Pcosα+Qsinα=N
(2)
式中:α为最大轮缘倾角;μ为轮缘与钢轨侧面的摩擦因数。
(3)
我国GB5599—85规定,当横向作用力Q的作用时间大于0.05 s时,脱轨系数的容许值和安全值如下:
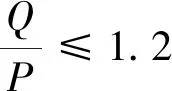
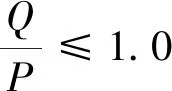
1.2.2轮对横移量
当轮对中心离开对中位值向右移动yw时,则左右侧车轮的实际滚动圆半径分别为:
RL=R0-λyw
(4)
RR=R0+λyw
(5)
式中:R0、RL、RR分别为名义滚动圆半径以及左右轮的实际滚动圆半径;λ为车轮踏面锥度。令车轮踏面锥度为常数,当存在轮径差时,车轮轮对中心偏离轨道中心线的距离可以表示为
yw=(RR-RL)/2λ
(6)
当机车转弯时,机车要在直线轨道行驶时偏移基础之上再次偏移,转弯时再次偏移的距离可通过式(7)计算:
ye=dR0/λR
(7)
式中:ye为轮对横移量;R为曲线的半径;d为轮对的2个滚动圆之间的距离。
1.2.3轮轨横向力
过大的轮轨横向力会扩宽导轨距离,拔起道钉甚至破坏导轨线路。因此,轮轨间的最大横向力应当受到限制。其标准如下:
1) 道钉拔起,道钉应力为弹性极限的限度为
Q≤19+0.3Pst
(8)
2) 道钉拔起,道钉应力为屈服极限的限度为
Q≤29+0.3Pst
(9)
3) 线路严重变形的限度:
木轨枕为
(10)
混凝土轨枕为
(11)
式中:Q为轮轨横向力(kN);H为轮轨横向力(kN);Pst、Pst1、Pst2分别为车轮平均、左轮、右轮静载荷(kN)。
2 动力学模型
本文以某机车为基础,利用SIMPACK软件建立了其多体动力学模型,机车模型如图2所示。机车由轮对、构架、车体、一系悬挂和二系悬挂组成。轮对质量为1 t,构架质量为3 t,车体质量为32 t。机车的悬挂参数如表1所示。其自由度和拓扑关系如图3所示。
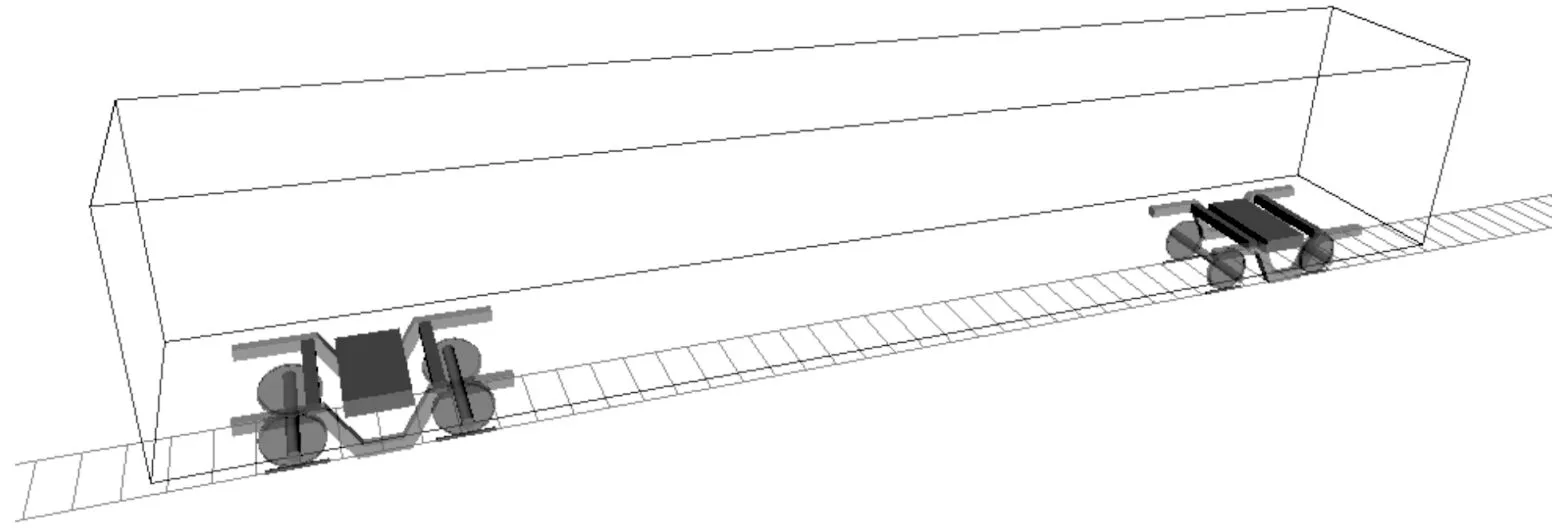
图2 机车多体动力学模型
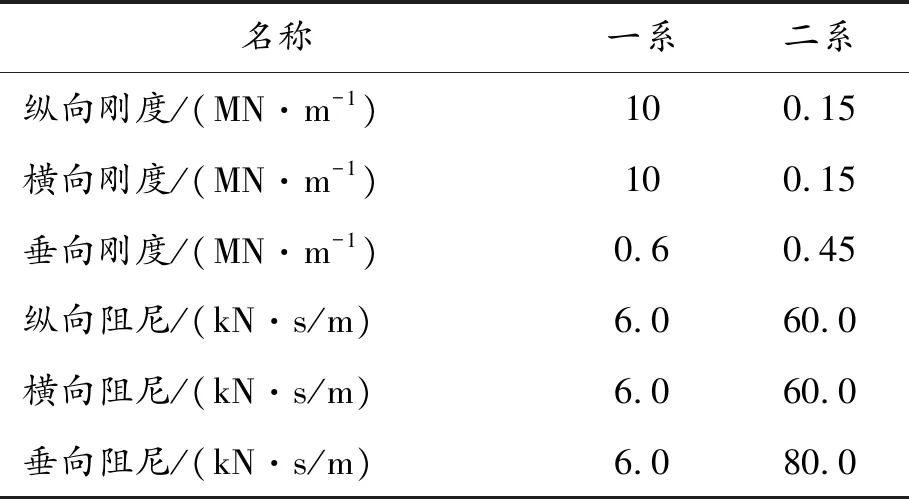
名称一系二系纵向刚度/(MN·m-1)100.15横向刚度/(MN·m-1)100.15 垂向刚度/(MN·m-1)0.60.45纵向阻尼/(kN·s/m)6.060.0横向阻尼/(kN·s/m)6.060.0垂向阻尼/(kN·s/m)6.080.0
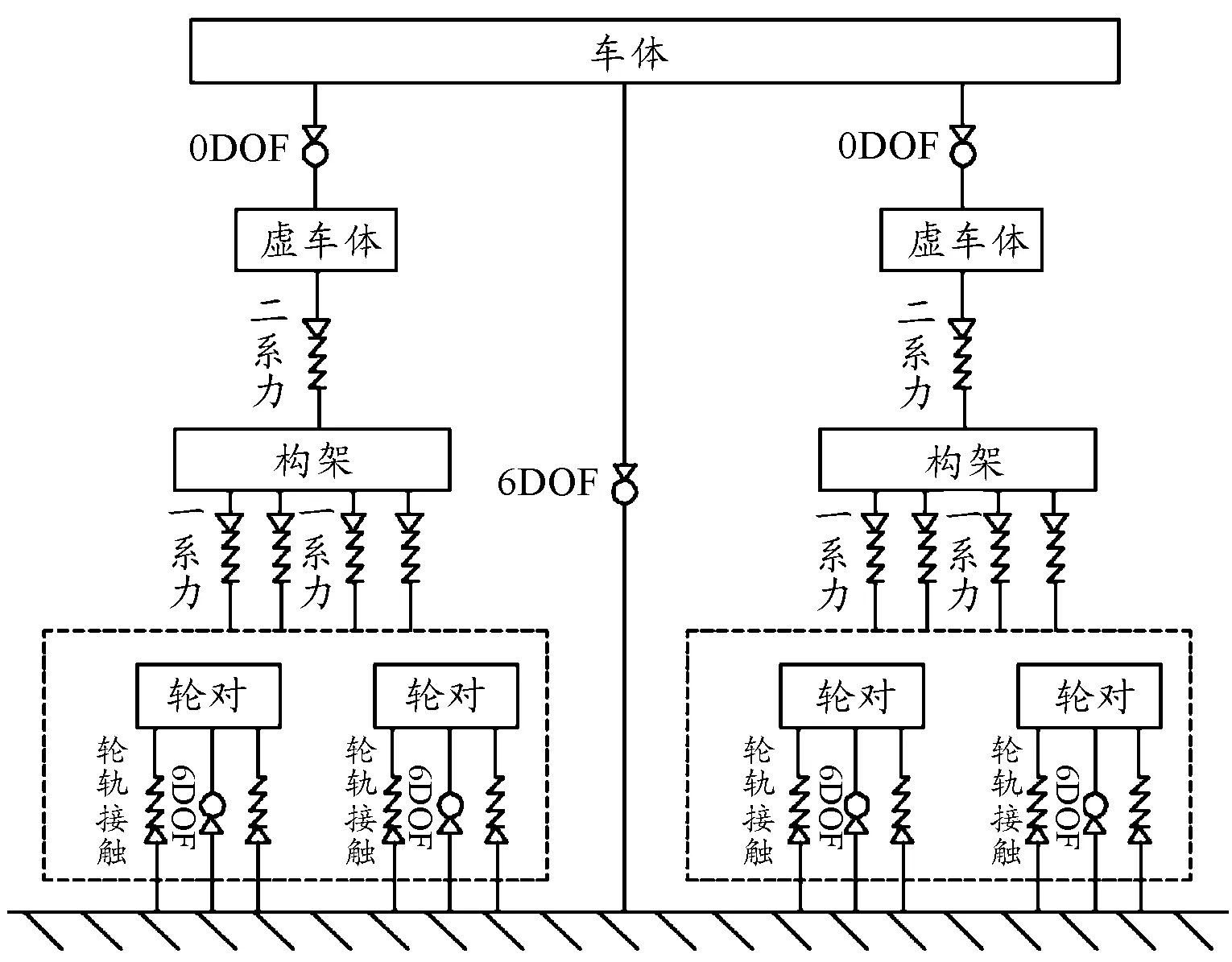
图3 机车的结构拓扑图
3 轮径差对机车安全性影响分析
由前面分析可知:轮径差有4种典型的形式,分别是同相轮径差、反相轮径差、前轮对轮径差和后轮对轮径差;到辅修时,同转向架内轮径差不超过5 mm。因此,本文将在同一转向架内轮径差不大于3 mm的范围内研究4种典型轮径差对机车安全性能的影响。
3.1 机车直线行驶性能分析
轮径差的取值为0、0.5、1.0、1.5、2.0、2.5、3.0 mm,机车的运行速度分别取100、150、200 km/h。
机车的脱轨系数、轮对横移量和轮轨横向力随同相轮径差的变化如图4~6所示。
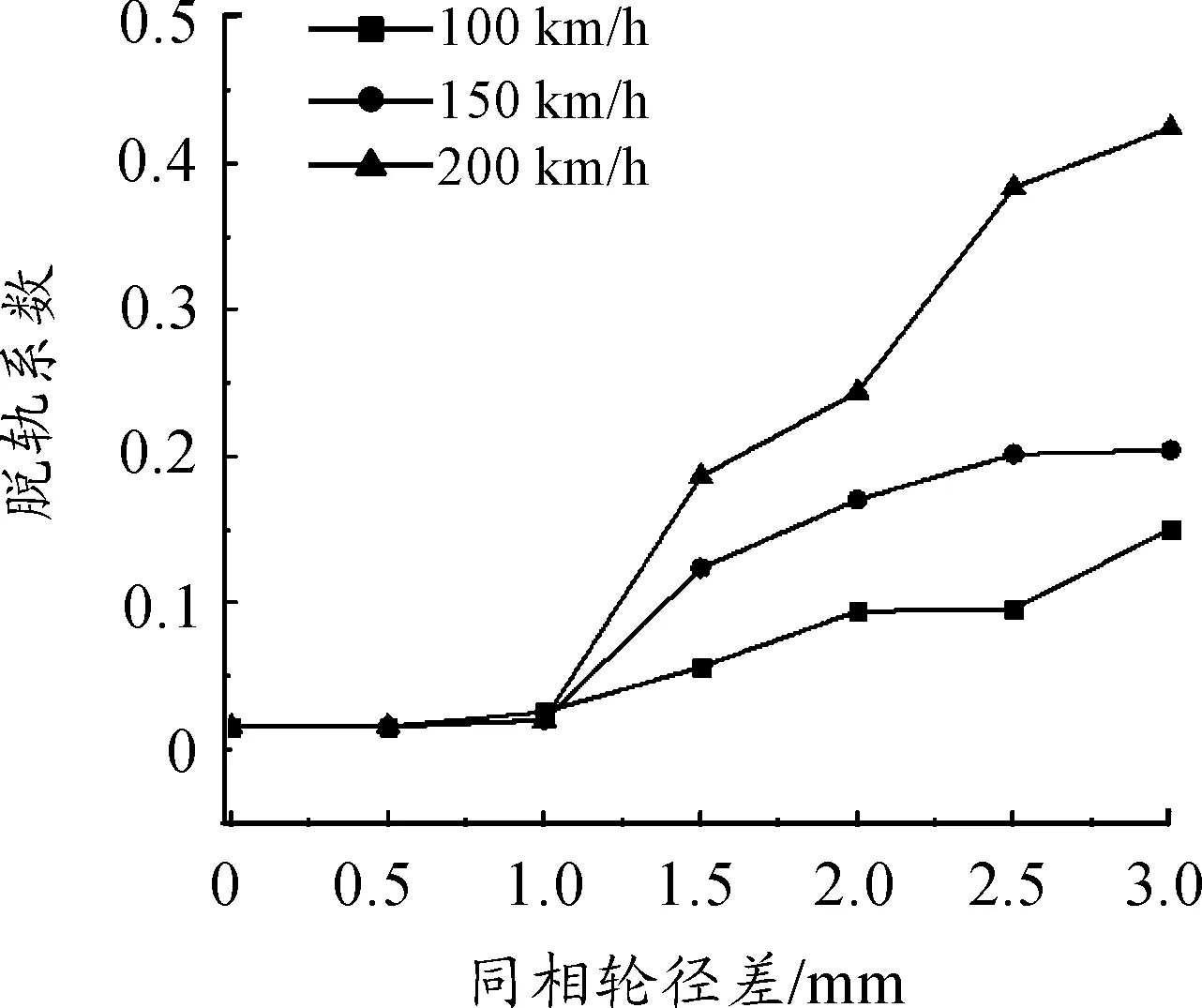
图4 脱轨系数随同相轮径差及速度的变化关系
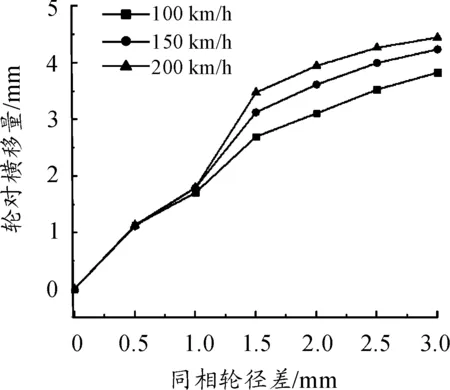
图5 轮对横移量随同相轮径差及速度的变化关系
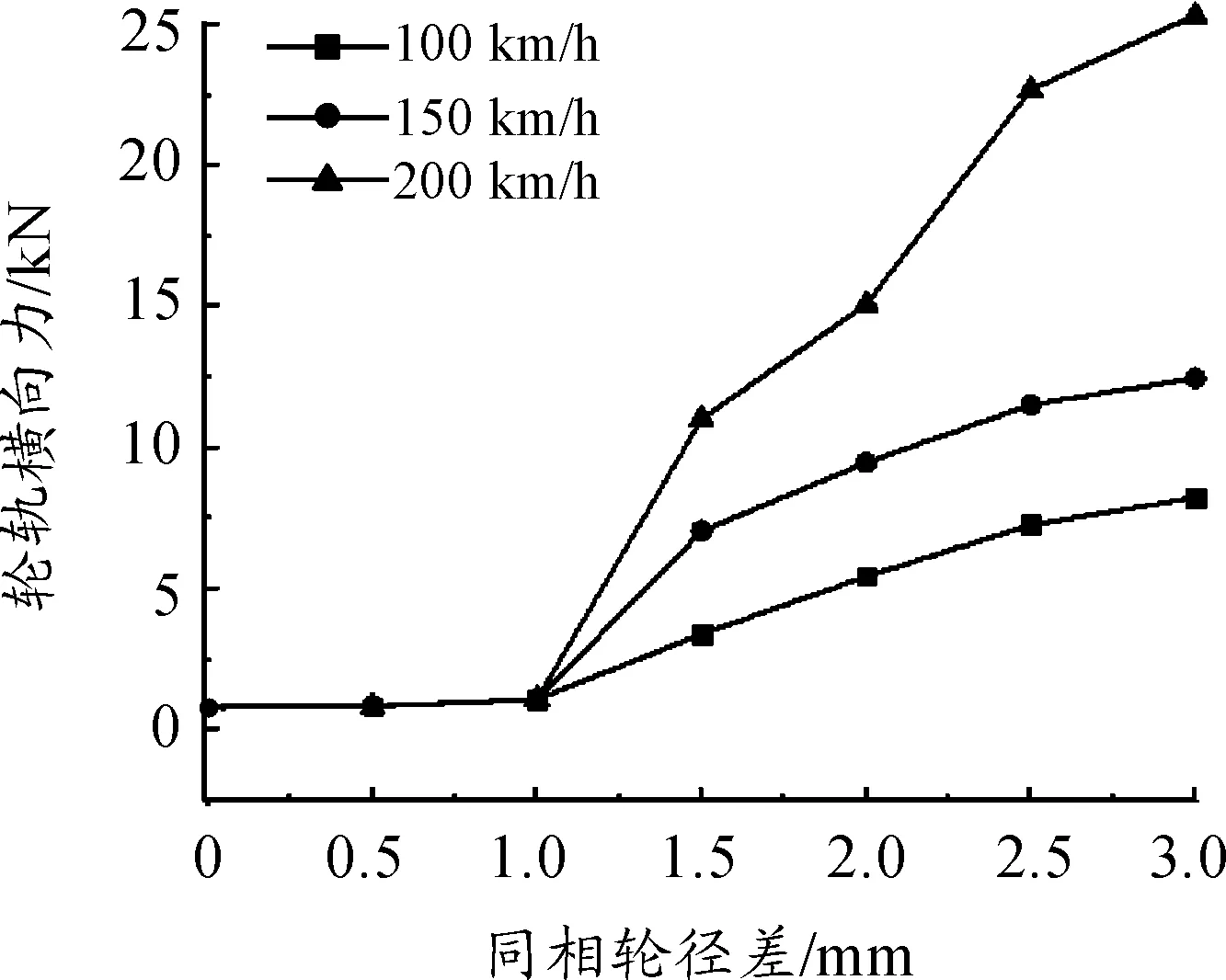
图6 轮轨横向力随同相轮径差及速度的变化关系
图4~6表明:
1) 随着同相轮径差的增加,轮对的脱轨系数、轮对横移量和轮轨横向力也逐渐增大。以速度为150 km/h为例,同相轮径差为1和3 mm时,脱轨系数分别为0.020 6和0.204 8,轮对横移量分别为1.79和4.23 mm,轮轨横向力分别为1.094和12.472 kN。
2)同相轮径差在1 mm以内、速度不变时,脱轨系数和轮轨横向力随着同相轮径差的增大变化很小,而轮轨横移量变化较大。以机车速度为150 km/h时为例,同相轮径差为0.5和1 mm时,脱轨系数分别为0.016 5和0.020 6,轮对横移量分别为1.11和1.79 mm,轮轨横向力分别为0.849 6和1.094 kN。
3)当同相轮径差在1 mm以内时,机车的脱轨系数、轮对横移量和轮轨横向力不随速度的变化而变化。当同相轮径差大于1 mm时,脱轨系数、轮对横移量和轮轨横向力随着速度的增加而增加。以同相轮径差为0.5和2 mm为例,当速度分别为100、150和200 km/h,同相轮径差为0.5 mm时,3种速度下,脱轨系数均为0.016,轮对横移量均为1.129 mm,轮轨横向力均为0.849 kN;同相轮径差为2 mm时,脱轨系数分别为0.094 9、0.171和0.224,轮对横移量分别为3.1、3.61、3.94 mm。
机车的脱轨系数、轮对横移量和轮轨横向力随反相轮径差的变化关系如图7~9所示。
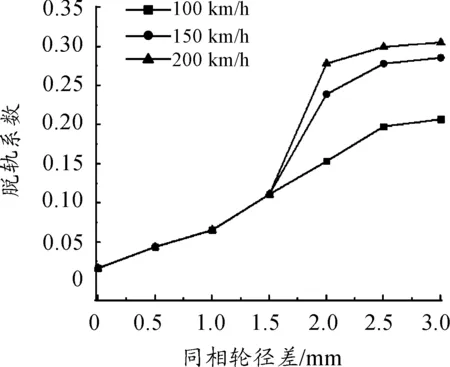
图7 脱轨系数随反相轮径差及速度的变化关系
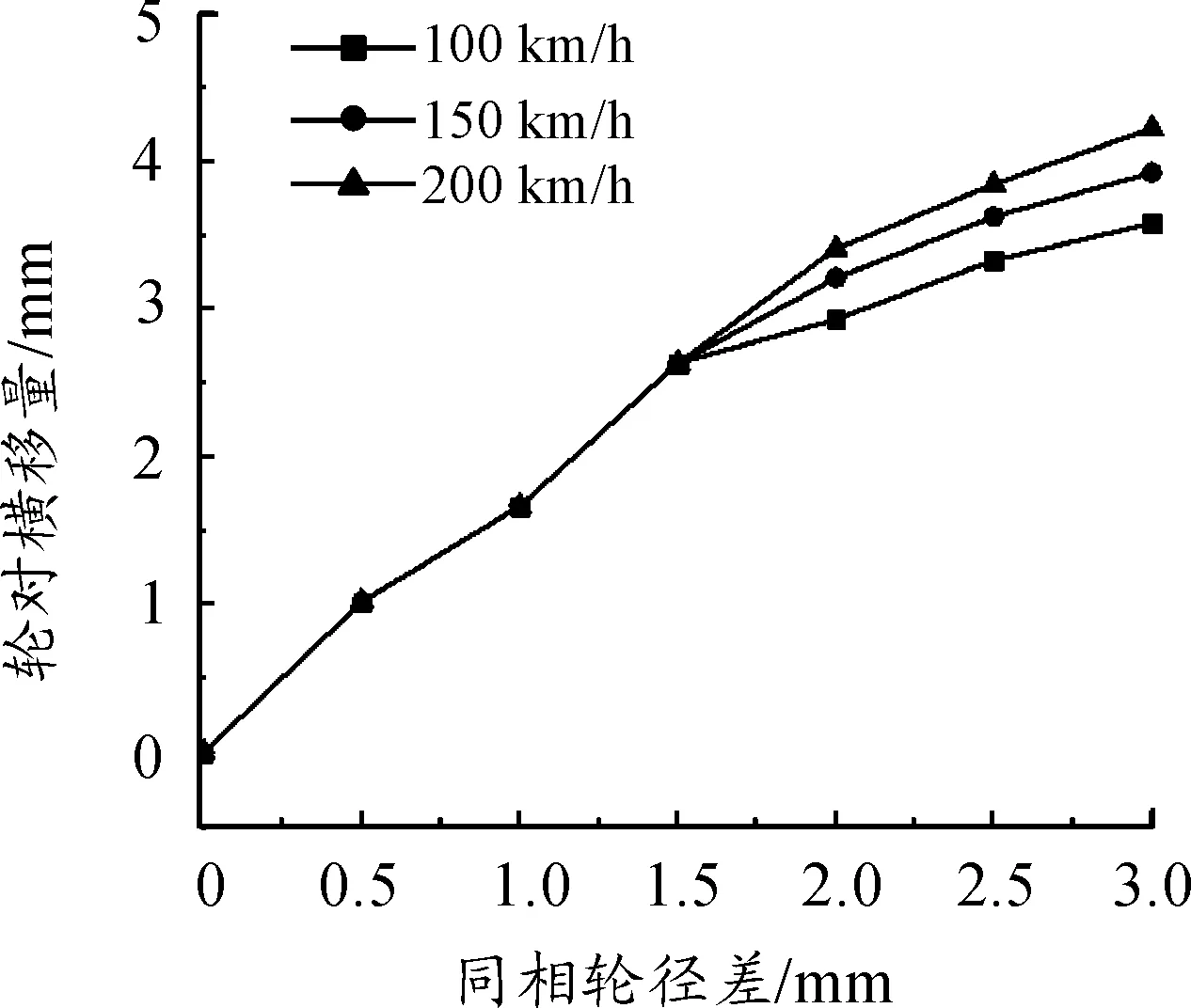
图8 轮对横移量随反相轮径差及速度的变化关系
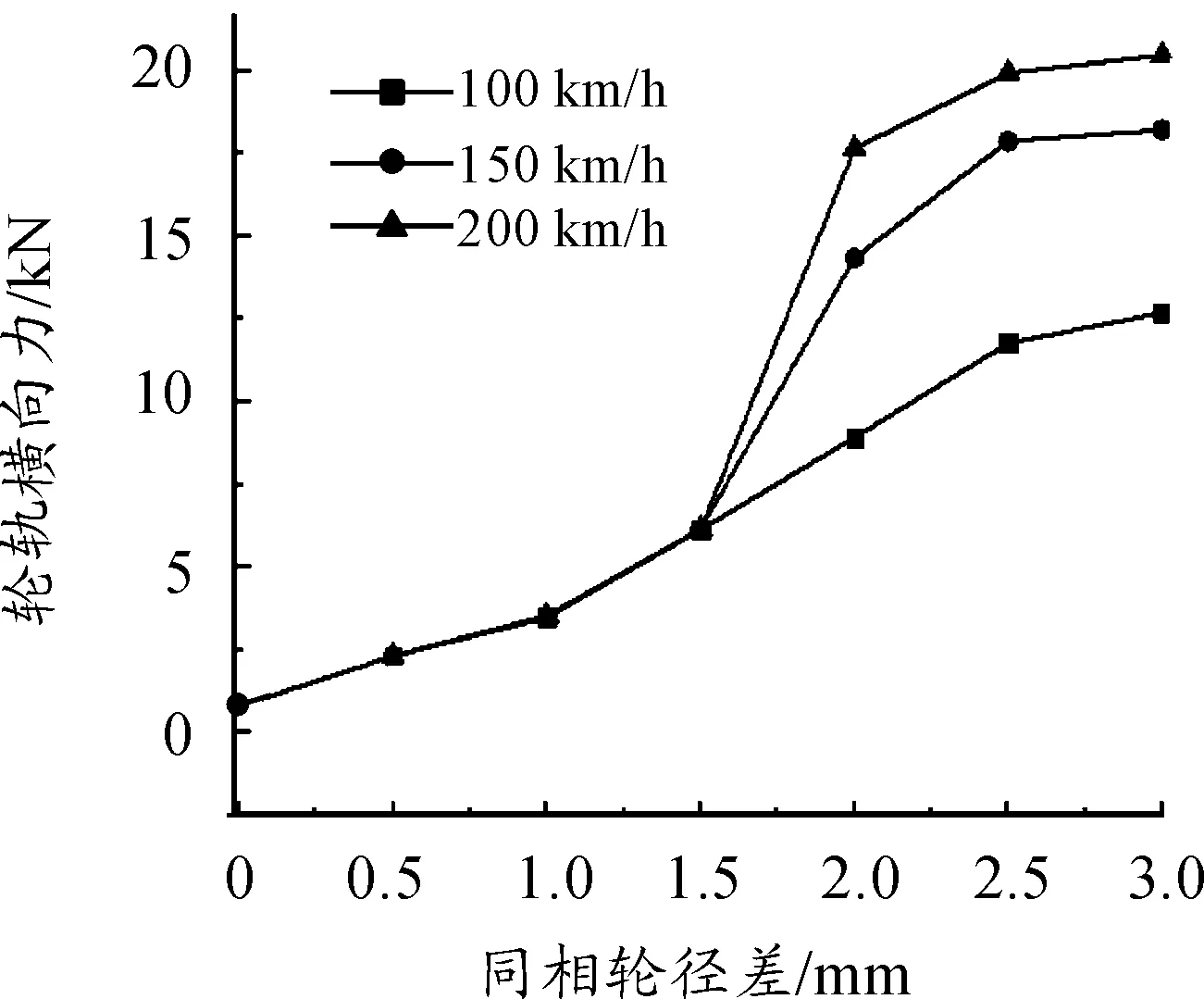
图9 轮轨横向力随反相轮径差及速度的变化关系
图7~9说明:
1) 机车的脱轨系数、轮对横移量和轮轨横向力随着反相轮径差的增大而增大。以机车速度100 km/h时为例,当反相轮径差为1 mm和3 mm时,机车的脱轨系数分别为0.064 7和0.206 3,轮对横移量分别为1.668和3.583 mm,轮轨横向力分别为3.486 9和12.694 kN。
2) 当反相轮径差在1.5 mm以内时,机车的脱轨系数、轮轨横移量和轮轨横向力不随机车速度的变化而变化。以反相轮径差为1 mm为例,当机车速度为100、150、200 km/h时,机车的脱轨系数均为0.065、轮对横移量均为1.668 mm、轮轨横向力均为3.488 mm。
3) 当反相轮径差大于1.5 mm时,机车的脱轨系数、轮对横移量和轮对横向力随着机车速度的增大而增大。以轮径差2 mm为例,机车速度分别为100、150、200 km/h时,机车的脱轨系数分别为0.152 8、0.238 5和0.277 7,轮对横移量分别为2.933、3.214和3.41mm,轮轨横向力分别为8.928、14.359和17.671kN。
图10~12是机车的脱轨系数、轮对横移量和轮轨横向力随前轮对轮径差的变化而变化的曲线。图10~12说明:
1) 机车的脱轨系数、轮对横移量和轮轨横向力随着前轮对轮径差的增大而增大。以机车速度100 km/h时为例,当前轮对轮径差为1和3 mm时,机车的脱轨系数分别为0.034 7和0.114 2,轮对横移量分别为1.689和3.454 mm,轮轨横向力分别为1.83和6.114 kN。
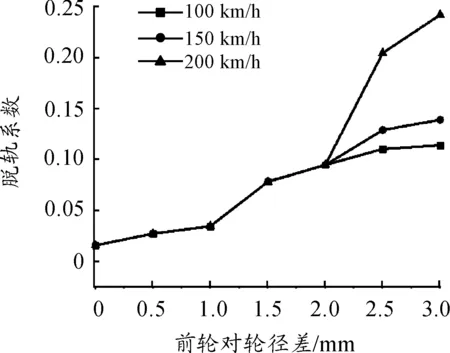
图10 脱轨系数随前轮对轮径差及速度的变化关系
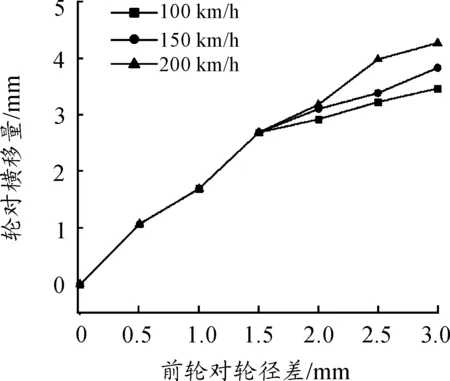
图11 轮对横移量随前轮对轮径差及速度的变化关系
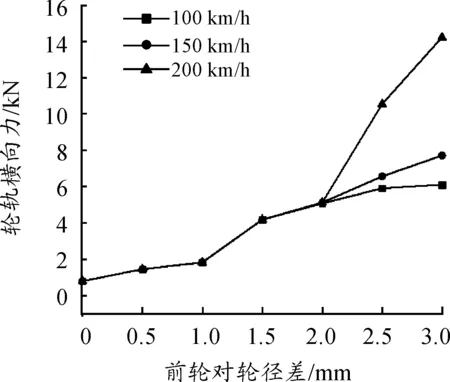
图12 轮轨横向力随前轮对轮径差及速度的变化关系
2) 当前轮对轮径差在1.5 mm以内时,机车的脱轨系数、轮对横移量和轮轨横向力不随机车速度的变化而变化。以前轮对轮径差1.5 mm为例,机车的速度为100、150和200 km/h时,机车的脱轨系数均为2.679,轮对横移量均为2.679 mm,轮轨横向力均为4.19 kN。
3) 当前轮对轮径差大于1.5 mm时,机车的脱轨系数、轮对横移量和轮轨横向力随着机车速度的增大而增大。以前轮对轮径差2.5 mm为例,当机车的速度为100、150和200 km/h时,机车的脱轨系数分别为0.110 6、0.129 1和0.204 7,轮对横移量分别为3.216、3.375和3.969 mm,轮轨横向力分别为5.914、6.011和10.511 kN。
机车的脱轨系数、轮对横移量和轮轨横向力随后轮对轮径差的变化而变化的曲线如图13~15所示。
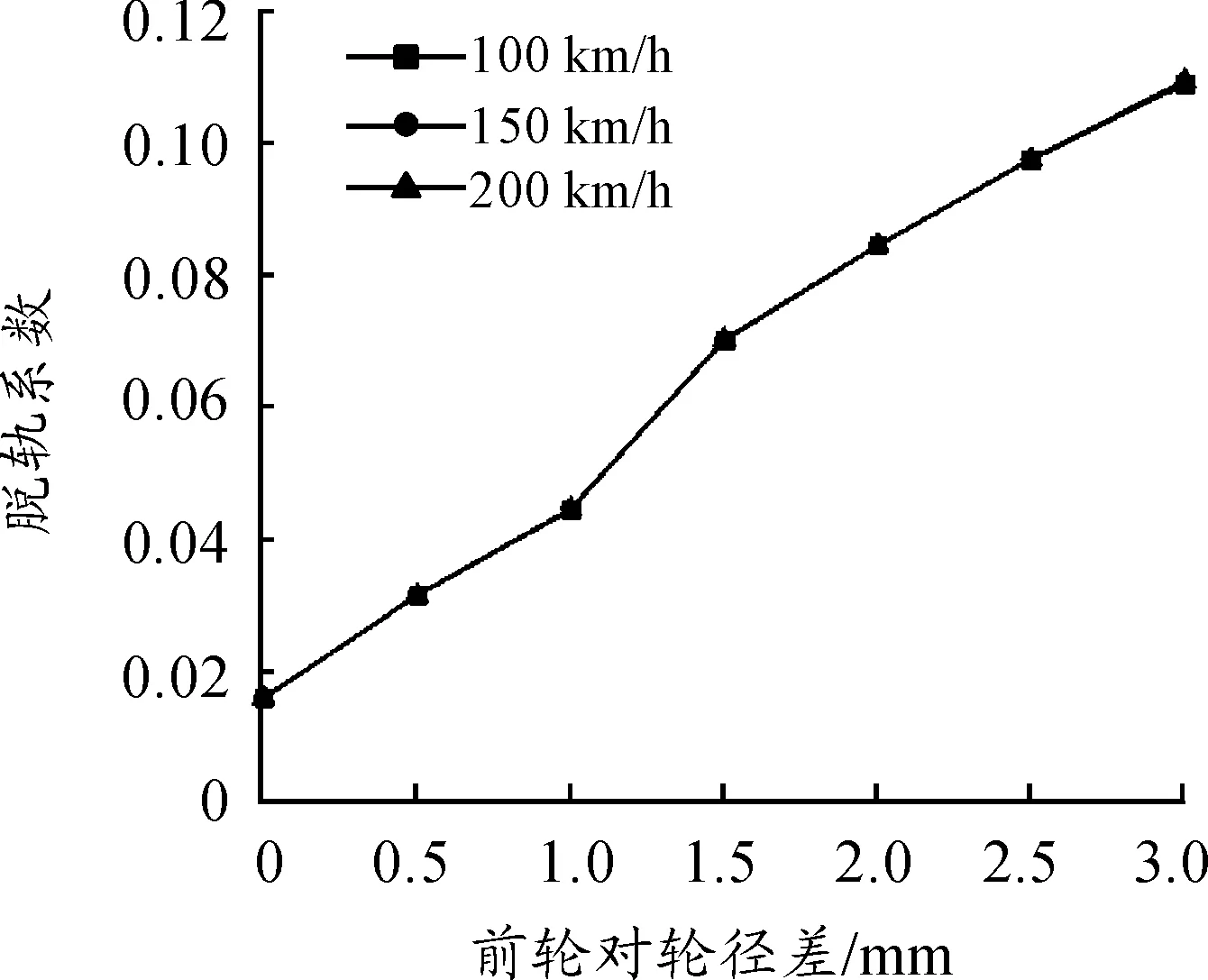
图13 脱轨系数随后轮对轮径差及速度的变化关系
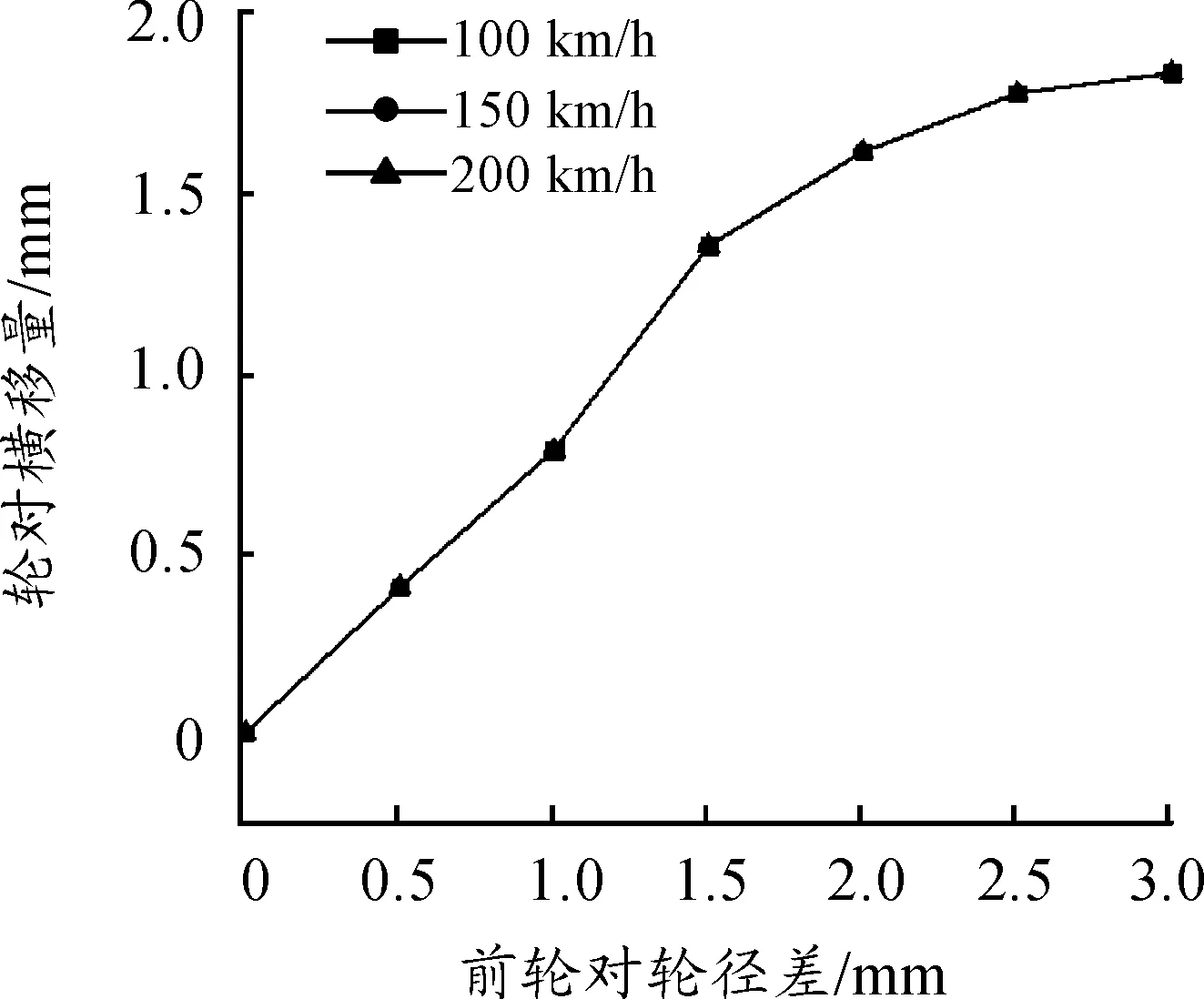
图14 轮对横移量随后轮对轮径差及速度的变化关系
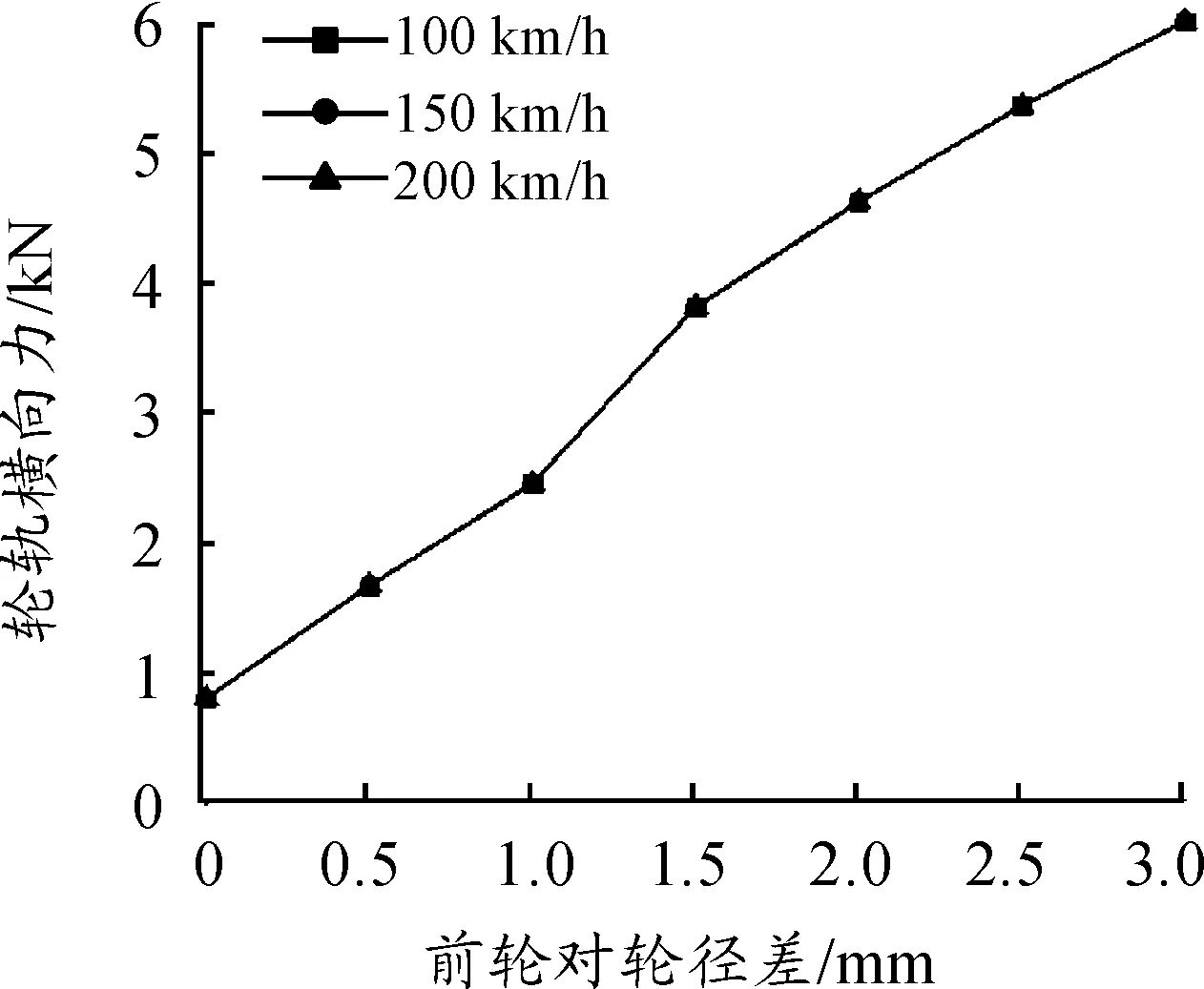
图15 轮轨横向力随后轮对轮径差及速度的变化关系
图13~15说明:
1) 机车的脱轨系数、轮对横移量和轮轨横向力随着后轮对轮径差的增加而增加。以速度100 km/h时为例,当后轮对轮径差为1和3 mm时,机车的脱轨系数分别为0.046 3和0.109 3,轮对横移量分别为0.737和1.838 mm,轮轨横向力分别为2.645和6.040 kN。
2) 当后轮对轮径差在3 mm以内时,机车的脱轨系数、轮对横移量和轮轨横向力不随机车速度的变化而变化。以后轮对轮径差为2 mm为例,当机车速度为100、150和200 km/h时,机车的脱轨系数均为0.084 7,轮对横移量均为1.618 mm,轮轨横向力均为4.646 kN。
3.2 机车的曲线行驶性能分析
机车的轨道是由直线—缓和曲线—圆曲线—缓和曲线—直线组成。开始段直线长度为100 m,缓和曲线长度为120 m,圆曲线长度为100 m,结束段直线长度为1 000 m,取外轨超高0.11 m,缓和曲线起始时的曲率为0,缓和曲线末端的半径为700 m,圆曲线的半径为700 m。
当机车通过曲线时,其脱轨系数、轮对横移量和轮轨横向力随同相轮径差、反相轮径差、前轮对轮径差和后轮对轮径差的变化而变化的情况如表2~4所示。
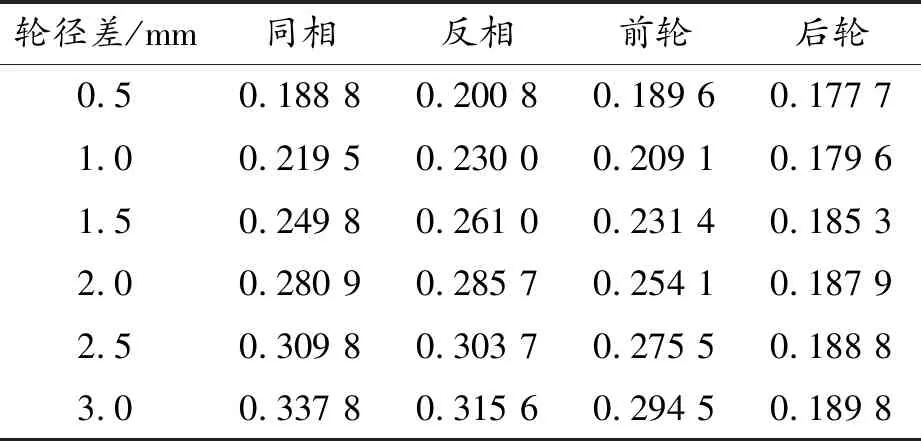
表2 机车的脱轨系数
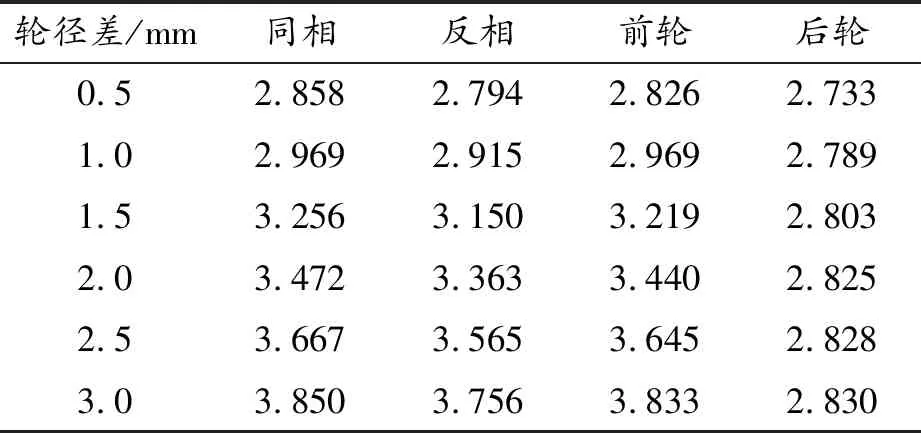
表3 机车的轮对横移量 mm
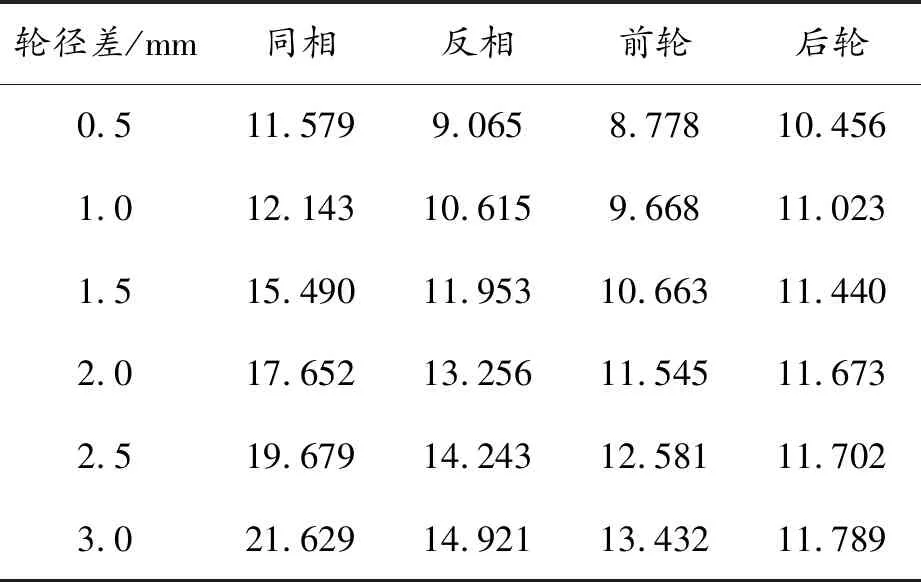
表4 机车的轮轨横向力 kN
表1~3说明:
1) 当机车曲线行驶时,机车的脱轨系数、轮对横移量和轮轨横向力随着4种轮径差的增大而增大。以同相轮径差为例,当轮径差为0.5和3 mm时,机车脱轨系数分别为0.188 8和0.337 8,轮对横移量分别为2.858和3.850 mm,轮轨横向力分别为11.549和21.629 kN。
2) 当机车曲线行驶时,后轮对轮径差的变化对机车的脱轨系数、轮对横移量和轮轨横向力影响最小。轮径差从0.5到3 mm,同相、反相、前轮对和后轮对对应的脱轨系数分别增加了0.149 0、0.114 8、0.104 9、0.012 1;轮对横移量分别增加了0.992、0.962、1.007、0.097 mm;轮轨横向力分别增加了10.050、5.856、4.654、1.333 kN。
图16~18是当转向架的轮对为同相轮径差时,机车的脱轨系数、轮对横移量和轮轨横向力随时间的变化曲线。
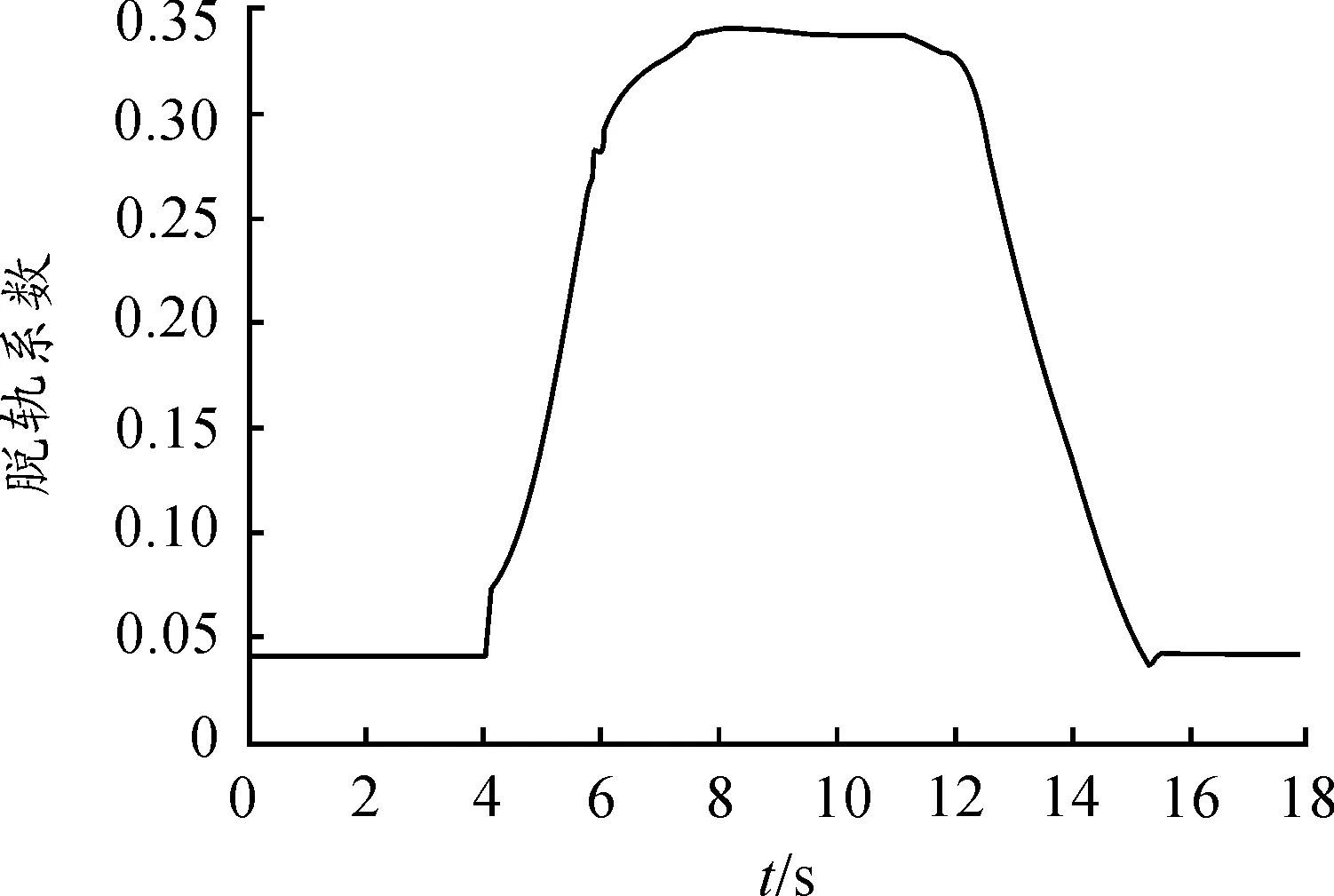
图16 脱轨系数随时间的变化关系
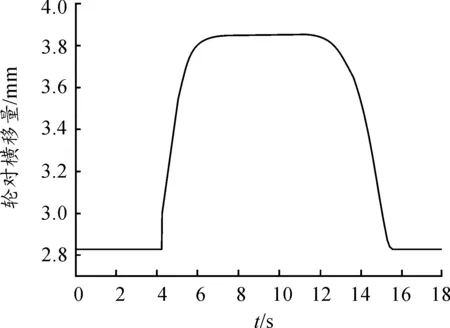
图17 轮对横移量随时间的变化关系
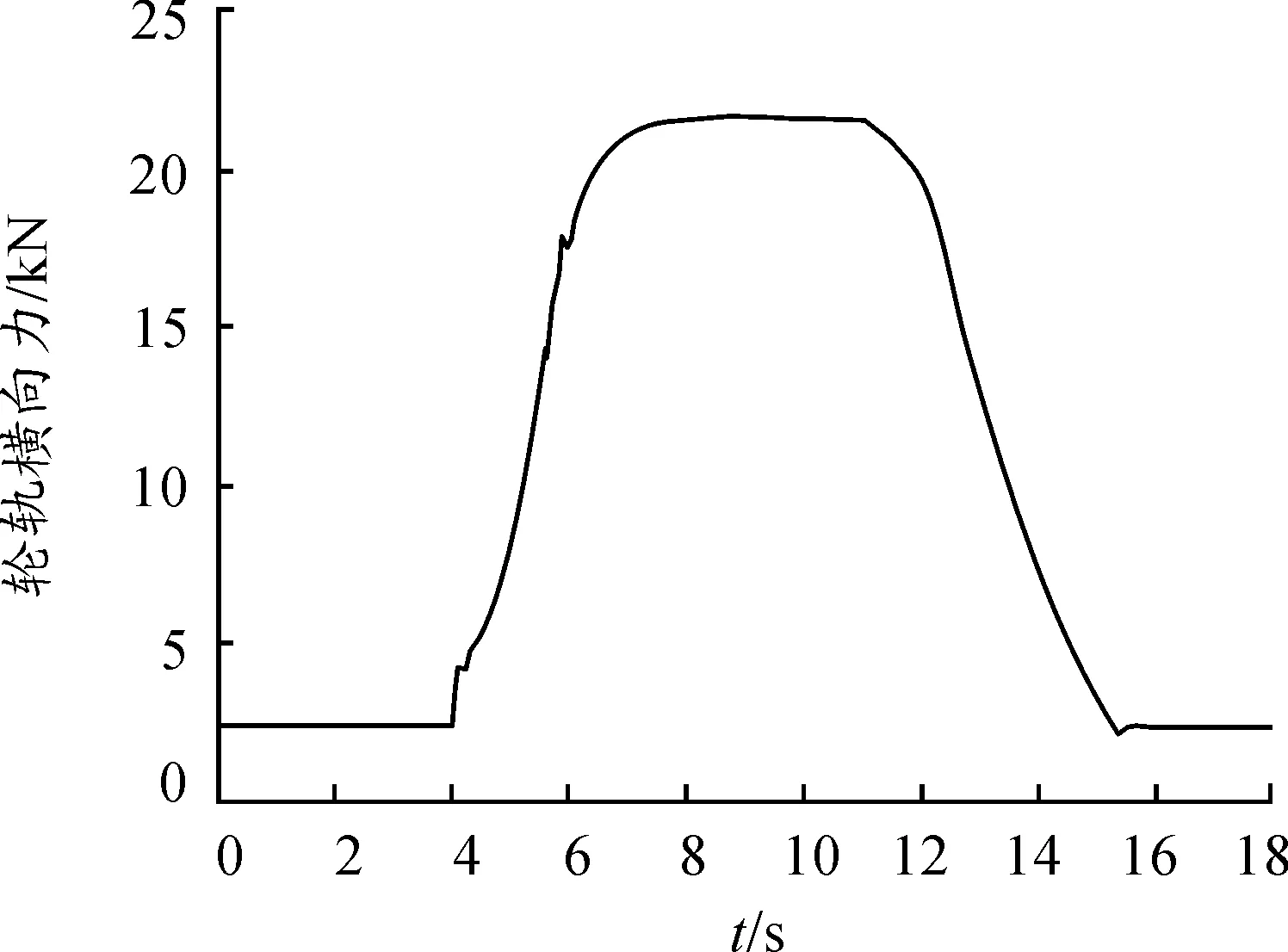
图18 轮轨横向力随时间的变化关系
从图16~18可以看出:机车通过曲线轨道时,轮轨之间的相互作用更为明显,机车从直线到缓和曲线再到圆曲线时,机车的脱轨系数、轮对横移量和轮轨横向力逐渐增大。
4 结论
1) 当机车在直线轨道运行时,机车的脱轨系数、轮对横移量和轮轨横向力均随轮径差的增加而增加。同时,当轮径差增大到一定值时,机车的脱轨系数、轮对横移量和轮轨横向力会受到机车速度的影响,速度越大,影响越大。当机车仅出现后轮对轮径差时,机车的速度变化对脱轨系数、轮对横移量和轮轨横向力无影响。
2) 在曲线运行时,随着各轮径差的增加,机车的脱轨系数、轮对横移量和轮轨横向力也逐渐增大。其中,后轮对轮径差的变化对轮轨安全性的影响最小。
3) 当机车出现轮径差时,应及时维修,防止发生倾覆和脱轨。
