基于迭代学习控制的岸桥小车定位控制仿真研究

周海燕，石 翠

（工业和信息化部电子第五研究所，广东 广州510610）

0 引言

在全球化背景下，国与国之间贸易越来越频繁，扮演国家级战略贸易港口的角色显得越来越重要，港口贸易和货船日益增多，岸桥小车在港口工作效率就显得十分重要，实现岸桥小车定位后减少甚至消除集装箱摇摆方面具有重要意义，提高岸桥效率的任务是提高港口效率的关键之一[1]。因此本文利用迭代学习控制[2]具有容易高效率计算量少的特点，使用开环PD型迭代学习控制方法进行仿真研究，得到了较好的仿真效果，对工程应用具有一定的参考价值。

1 动力学模型

小车吊重系统是经典的动态系统[3]。本文将小车吊重系统使用相对更好分析力学方法来建立其非线性数学模型，利用分析力学中广义坐标下拉格朗日方程对该系统进行描述。由于非线性方程的运算工作步骤太多了且算法较为紊乱，所以对其在假设的基础上做出了一些简化。线性化并化简后的小车-吊重动态方程如下公式：

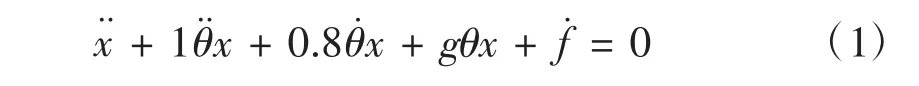
2 控制方案设计

2.1 迭代学习

迭代学习控制（简称为ILC）本身就具有重复性质[4]，所以对于有着类似运动特点的物体（如电梯、岸桥和数控机床等）能够提供良好的控制方法。与传统的控制方法不同，迭代学习控制只需要较少的先验学问和容易的计算量就可以很简单地处理不稳定性相对较高的高动态系统，而且适应性较强，易于实现目的。更重要的是，它并不依赖于一般精确的动态系统数学模型，而是一种迭代生成信息进而优化输入信号，使系统输出的数值尽最大可能地接近理想值的算法。实际上只要系统可重复运动或系统干扰呈现规则的周期性，ILC就可用于解决实际问题。

2.2 迭代学习原理

类型迭代学习控制通过先验知识系统和误差信息改进控制过程，不断改进系统以提高达到期望值，最终实现最佳控制[4]。受控过程的动态特征通常表示为：

考虑如下公式（2）的连续被控对象：

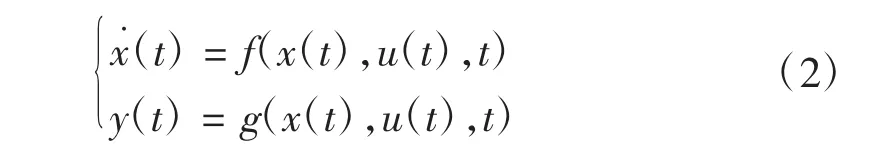
通过给定的学习律下使系统在时间t[0，T]内，多次进行重复运行（k趋向于∞），使实际输出向期望输出靠拢。迭代学习原理流程如图1所示。

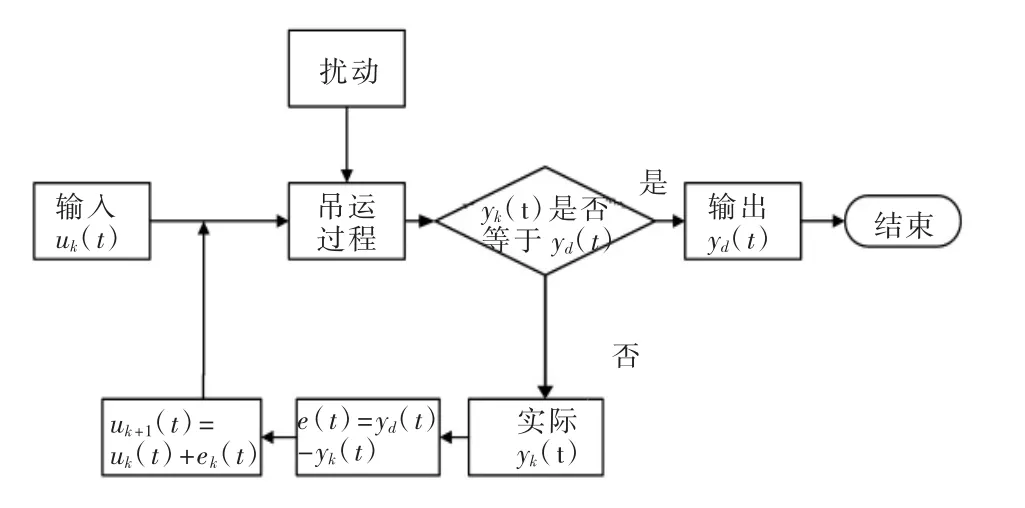
图1 迭代学习原理流程图

ILC算法研究也即如何利用前一个输入uk-1（t）和输出误差ek-1（t）来构造当前运行的控制输入uk（t）即确定uk（t）=L（uk-1（t），ek-1（t）），其中ek-1（t）=yd（t）-yk-1（t）为前次运行的输出误差，同时还需分析算法收敛性。

3 岸桥定位控制设计

3.1 迭代学习控制器结构的选取

由于岸桥作业条件恶劣无法满足测量控制对象的输出信号准确的要求在闭环控制上，所以选择拥有更快的响应速度开环控制。考虑添加积分I项后的PID控制，可以消除稳态偏差，但系统需要平稳的时间延长，不能满足快速响应的要求。本文采用基于PD型的开环结构来设计迭代学习控制器。

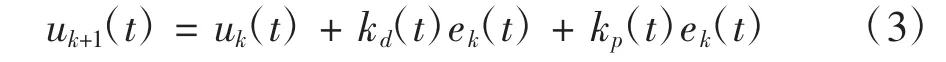
式中：kp、kd分别为PD学习增益矩阵，控制输入为uk（t），误差为ek（t）。

3.2 吊重系统期望轨迹

在吊具的角度传感器的测量下，一些有着丰富经验的操作人员能够根据货箱的体积大小安置其位置以及小车定位信息来不断调节小车速度，从而准确无误停放指定位置，同时可以在一定程度上减少吊重集装箱间的摇摆。以上所有操作测得的部分数值为摆角值（表1）。通过多项式曲线拟合的方式计算得出具体方程如下式：

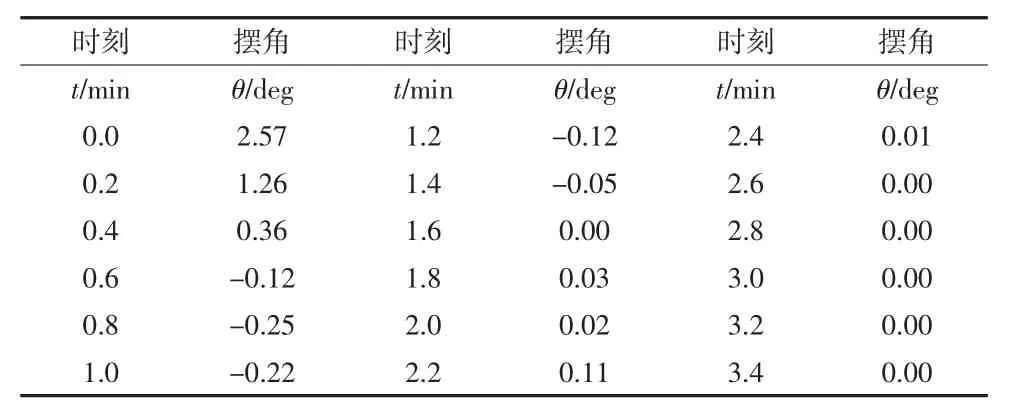
表1 实测吊重摆角

反复仿真校验最后得到PD模块的整定参数为：KP=0.5，KD=0.09。

反复仿真校验，最后得到PID模块的整定参数为：KP=0.27，KI=-0.003，KD=5.35。

4 仿真实验结果

取小车质量M=5 kg，吊重质量m=2.5 kg，绳长l=1 m，g=9.8 m/s2，设置迭代停止条件为迭代5次后停止，如图2所示。

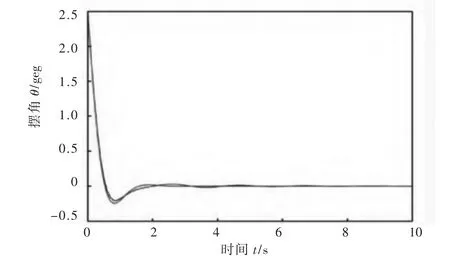
图2 仿真结果图

从迭代计算输出的结果可以发现输出轨迹与期望轨迹误差在0.01°左右，效果已经达到相当理想。

5 总结

港口岸桥是一个非线性、时变、不确定性和强耦合的复杂系统。使用迭代控制系统能够很好的适应并改善岸桥这种非线性，具有重复性的复杂系统。仿真数据表明迭代学习控制算法有效地控制了集装箱的摇摆，减少了人为操作小车定位的时间。