基于数据驱动的过热蒸汽温度系统模型辨识
2019-09-18王欢饶政华廖胜明
王欢,饶政华,廖胜明
(中南大学能源科学与工程学院,湖南长沙,410083)
火电机组的深度调峰和灵活性改造对超临界机组的建模和优化控制提出了更高要求[1-3]。过热蒸汽温度是机组运行过程中非常重要的控制参数,其过高或过低都会影响机组运行的经济性和安全性[4-5]。过热蒸汽温度对象具有非线性、大惯性和时变性等特点,随着机组容量的增加,响应的迟延和惯性增大,增加了过热蒸汽温度的控制难度。过热蒸汽温度的动态特性分析和模型辨识是提高其控制性能的基础[6]。采用机理建模方法得到的模型物理意义明确,通用性强。章臣樾[7]建立了锅炉整体的机理模型,研究了锅炉动态特性;徐啸虎等[8]建立了一种新的单相受热管集总参数动态数学模型;闫水保等[9]针对热工对象低通滤波特性,以单相受热过热器为对象,提出了适用于不同工况的通用传递函数。然而,机理建模所需对象信号采集量大,包含大量设计参数与试验参数,需要依靠许多经验公式,造成机理模型精度一般不高。目前,安全联锁仪表系统(SIS)已普遍应用于电厂,从海量的运行数据中挖掘热工系统的动态特性成为研究热点。孙灵芳等[10]采用大量历史数据和改进的神经网络(BP)算法建立了过热蒸汽温度的非线性模型;WANG 等[11]提出了以单位负荷为时变参数的非线性(LPV)模型,利用改进的量子群优化算法结合现场数据辨识模型参数;韩璞等[12]研究了多变量系统辨识过程中不能精确量化每个子系统数学模型的问题。ZHENG等[13]利用改进的粒子群算法(PSO)解决非线性系统参数辨识,实现了机械手控制系统的参数识别。辨识建模结构简单,所需参数较少,但系统辨识的实质是函数拟合的过程,在建模过程中缺乏透明性。为此,本文作者采用集总参数法对喷水减温器和过热器建立传递函数表达式模型,通过机理模型的推导得出模型辨识所需采集的变量,利用电厂现场数据(减温水量、减温器出口温度、高温过热量器出口温度)和粒子群算法对模型参数进行辨识,精确量化喷水减温器出口温度对减温水流量、高温过热器出口温度对减温器出口温度的传递函数关系式,并用不同时间段的运行数据对模型进行仿真验证,以便为过热蒸汽温度系统控制的仿真与优化研究提供参考。
1 数学模型
图1所示为某电厂超临界直流锅炉过热器的流程图。过热蒸汽从低温过热器进入屏式过热器加热,中间采用喷水减温器来调节过热蒸汽温度,最后通过高温过热器进入透平作功。喷水减温器的减温水从锅炉给水泵的中间阶段抽出,通过主、副控制器的命令控制阀门开度调节喷水流量。为研究模型入口扰动对模型出口参数变化的动态特性,建立喷水减温器、过热器模型。模型引入假设条件如下[7,10]:1)水平烟道进口烟气物性均为常数;2)减温器出口减温水已完全汽化,且与管内过热蒸汽在轴向具有相同的速度;3)减温器入口蒸汽与减温水的各种状态参数不随时间变化,混合流体的状态参数仅沿流动方向变化;4)减温器管道内各横截面上介质的状态参数均匀一致;5)减温器管壁与外界环境之间绝热;6)忽略减温器金属壁面轴向传热和管内径向温度梯度。
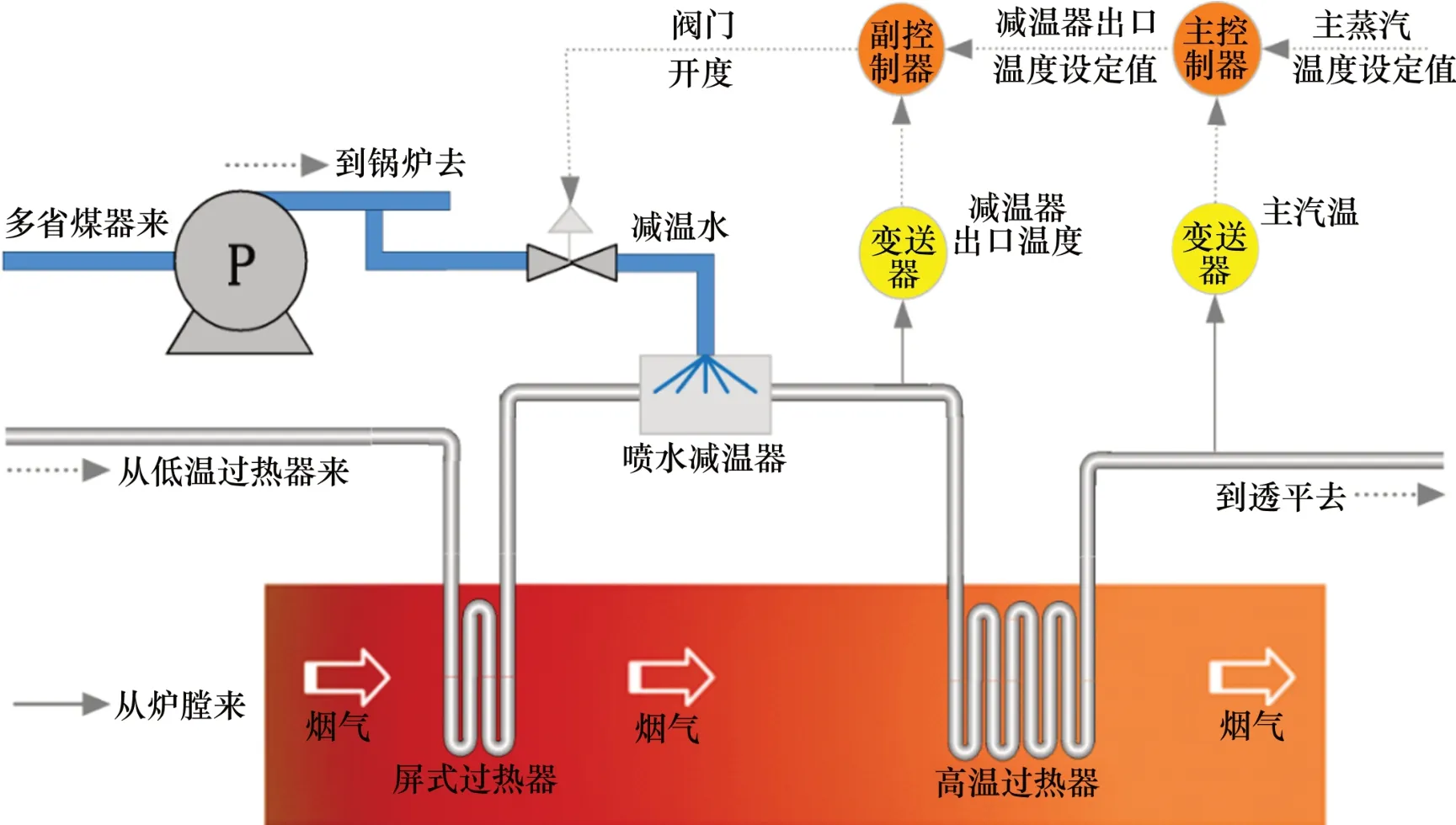
图1 超临界直流锅炉过热系统示意图Fig.1 Schematic diagram of overheating system of supercritical once-through boiler
1.1 减温器模型
超临界直流锅炉调节过热汽温的主要方式是在屏式过热器与高温过热器入口设置2个喷水减温器,将减温水直接喷入过热蒸汽达到调温的目的。以末级喷水减温器为例,建立喷水减温器出口蒸汽温度对减温水流量扰动的传递函数方程。以喷水减温器出口点参数为集总参数,联立质量平衡、能量平衡方程,进行线性化、偏差化处理后经过拉氏变换可得[14]
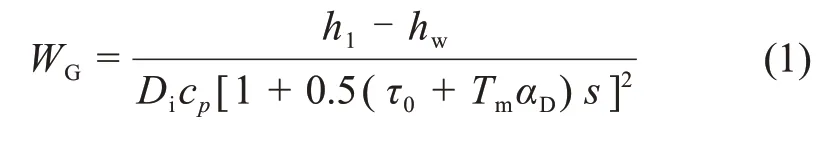
式中:h1和hw分别为减温器入口蒸汽和减温水的焓;Di为减温器出口蒸汽的质量流量;cp为减温器出口比定压热容;τ0为蒸汽流过喷水减温器的时间;Tm为金属蓄热时间常数;αD为动态参数。
由于τ0远小于TmαD,在实际计算过程中一般忽略不计,故式(1)可进一步简化为

喷水减温器传递函数模型参数为:惯性部分的阶次n=2;系统增益系统惯性时间常数T=0.5TmαD。
1.2 过热器模型
在负荷稳定的运行工况下,入口工质流量、热流量变化不大,高温过热器出口温度主要受入口蒸汽温度变化的影响。取高温过热器出口点参数为集总参数,将管壁金属能量平衡方程和相关的传热方程进行线性化、偏差化处理,经过拉氏变换可得过热器出口蒸汽温度与减温器出口蒸汽温度的传递函数方程[9]:
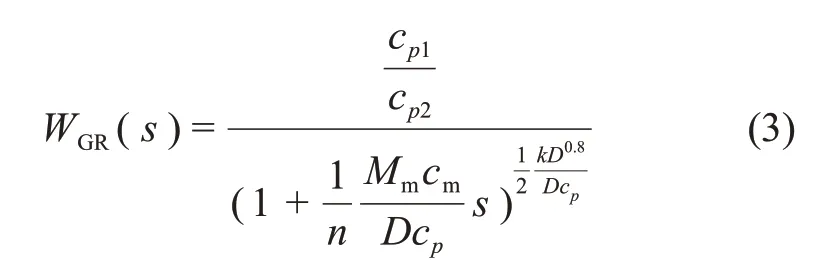
根据上述分析,选择2个高阶惯性环节进行模型辨识,即
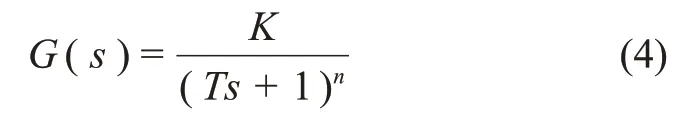
1.3 粒子群算法
在标准粒子群算法的基础上加入自适应动态惯性权重和异步变化学习因子策略,并在算法中引入“自然选择”的思想,克服易陷入局部最优和后期收敛速度慢的情况。在每一次迭代中,粒子通过跟踪2 个“极值”来更新:一是个体极值Pbest,记为Pi=(pi,1pi,2…pi,d);二是全局最优解Gbest,记为Pg=(pg,1pg,2…pg,d)。粒子更新速度和位置的公式为[15]:
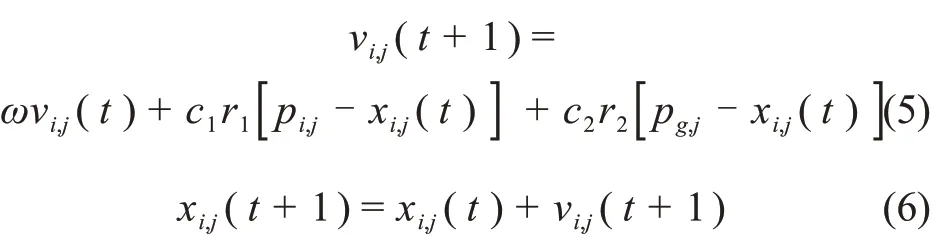
式中:ω为惯性权重,其计算式为[16]
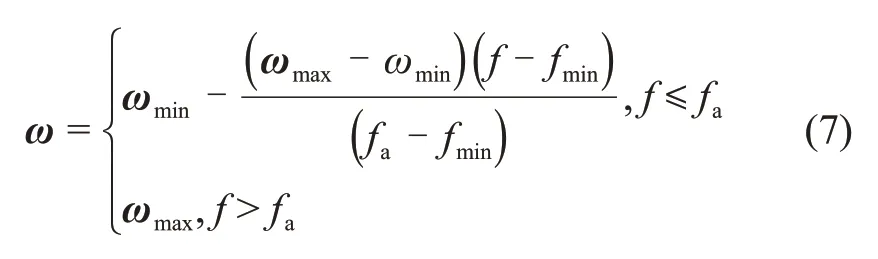
c1和c2为学习因子,其计算式为[17]:
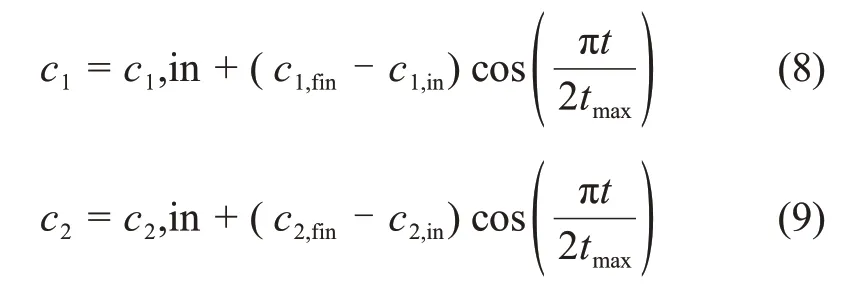
式中:i=1,2,…,n;j=1,2,…,d;r1和r2为随机数;t为当前迭代次数;ωmax和ωmin分别为ω的最大值和最小值;f为当前粒子的适应度;fa和fmin分别为当前所有粒子的平均适应度和最小适应度;c1,in和c2,in分别为c1和c2的初始值;c1,fin和c2,fin分别为c1和c2迭代终值;tmax为最终迭代次数。
本文中,优化的目标函数为:
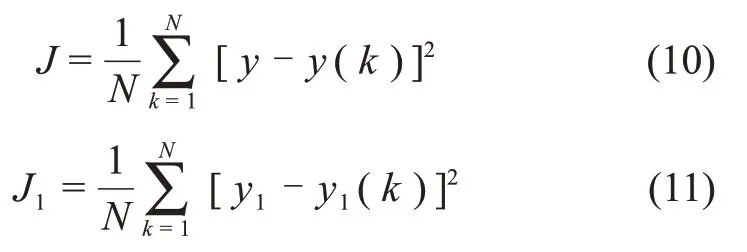
式中:J和J1为粒子的适应度函数;y和y1分别为减温器出口温度和过热器出口温度预处理后值;y(k)和y1(k)分别为模型实际激励下输出的减温器出口温度和过热器出口温度;N为采样长度。
1.4 计算方法
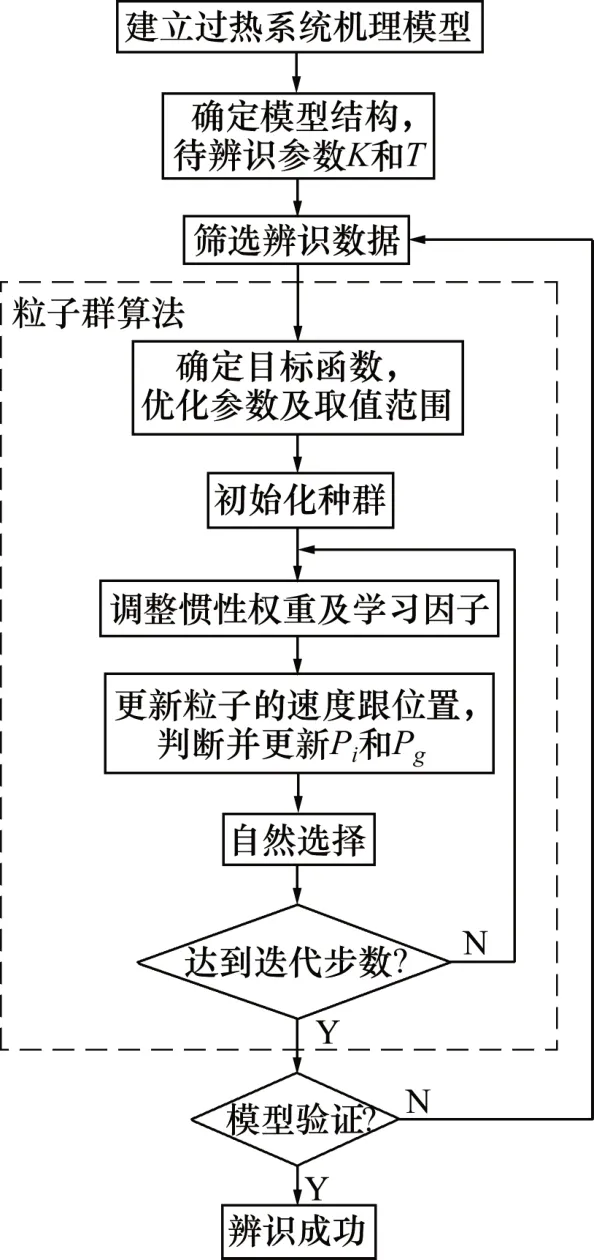
图2 模型辨识流程图Fig.2 Flow chart of model identification
模型辨识步骤如图2所示。根据建立的减温器与过热器机理模型,选择辨识模型。根据式(2)和(3),需要采集的数据信号为减温器出入口蒸汽温度、减温水流量和温度、主蒸汽流量、主蒸汽压力、总给煤量。本文通过稳态检测筛选辨识数据,将传递函数差分化,利用粒子群算法对模型参数在论域内反复寻优,达到迭代步数时即停止计算并输出结果;经过不同时期数据验证模型的可靠性。
2 结果与讨论
不同负荷下热工系统的传递函数不同,本文选择3 种典型工况(分别为400,550 和600 MW)下的稳态数据段进行辨识,采用粒子群算法对减温器、过热器模型参数反复寻优并验证辨识结果。稳态条件为:主蒸汽流量波动范围不超过其均值的1%,总给煤量波动范围不超过1.2%,主蒸汽压力的波动范围不超过其均值的1%。数据来源为某电厂实际运行数据,将挑选出的数据段通过五点三次平滑算法滤波、粗大值处理和零初始化处理[18]。
2.1 喷水减温器模型辨识
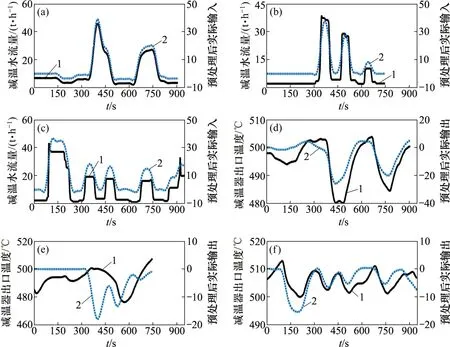
图3 3个工况下减温器模型的辨识数据Fig.3 Identification data of desuperheater model under three operating conditions
减温水流量和减温器出口蒸汽温度预处理前后数据如图3所示。如图3(a),(b)和(c)所示,减温水流量是1个阶跃激励信号,处理后的数据具有零初始值并且过滤了噪声使得数据更加光滑。如图3(d),(e)和(f)所示,处理后减温器出口温度减去相应的入口蒸汽温度,以消除入口蒸汽温度波动对出口蒸汽温度的影响。减温器出口温度的数据处理前后波动变化较大,是因为在现场数据中对减温器出口温度产生影响除了减温水外,还包括给煤量、主汽压和给水量等其他变量,但又不属于噪声使得滤波效果对这一部分干扰无法消除。辨识的模型结构选择式(4),通过推导得出喷水减温器模型阶次为2,只需辨识参数K和T。粒子群算法设置为:种群规模M=100,最大迭代次数为N=1 000,ωmax=0.9,ωmin=0.4c1,in=2.5,c1,fin=1.25,c2,in=1.25,c2,fin=2.5,K∈[-100,0],T∈[0,300]。辨识结果如表1所示。从表1可见:减温器模型系统增益K、时间常数T随负荷增加而减小;随着锅炉负荷增加,蒸汽流量和燃料耗量按比例增大,但炉内辐射热并不按比例增加;屏式过热器出口蒸汽焓增减少,而主蒸汽流量增加,因此,K和T随着负荷增加而减小并符合系统实际特性。表1中适应度均在0.16以下且随负荷上升而降低,说明模型的辨识精度较高,且越接近设计工况,系统的可辨识性越强。
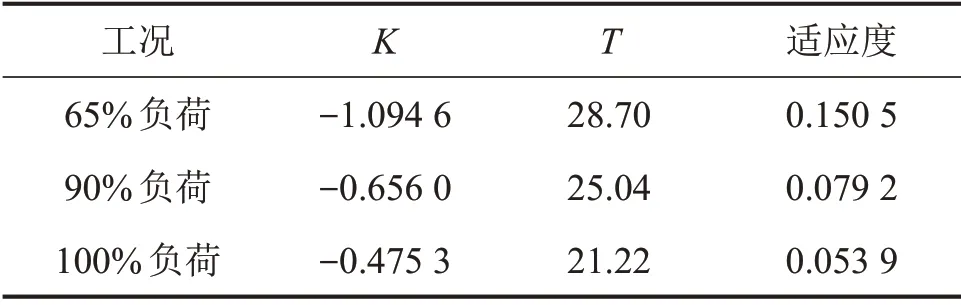
表1 不同工况下减温器模型辨识结果Table1 Desuperheater model identification results under different working conditions
图4所示为用不同时期的数据进行模型验证结果。将减温水量作为激励信号,并将建立的动态模型输出与相同激励条件下机组的实际输出进行对比。从图4可见:减温器出口温度都与减温水量变化趋势相反,减温水流量变大,减温器出口温度降低;减温水流量变小,减温器出口温度上升,符合现场运行情况。为进一步说明建模的精确度,计算实际输出温度与建立的模型在相同激励下温度输出的相对偏差,3种工况模型的最大相对偏差量分别为0.12%,0.21%和0.35%,说明辨识所得模型能较好地反映喷水减温器出口温度在减温水的扰动下的动态特性。
2.2 过热器模型辨识
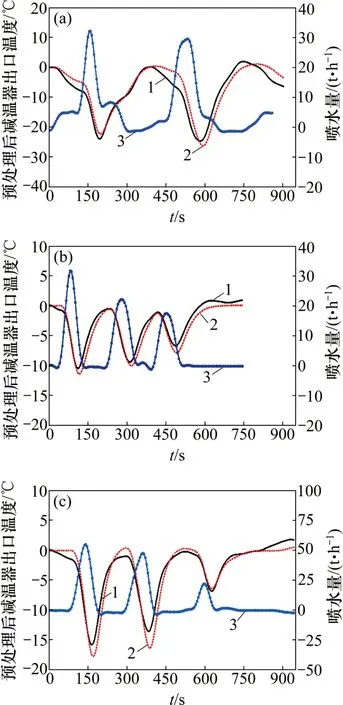
图4 3种工况下减温器辨识模型的验证Fig.4 Verification diagram of desuperheater model under three working conditions
由于过热器在实际运行过程中有较大的时滞性,本文采用灰色关联度分析法[19],通过过热器出口温度和入口温度在时间上的关联度来确定不同负荷下的迟滞时间,计算得到400,550 和600 MW 工况负荷下的迟滞时间分别为290,315 和360 s。确定延时时间后,对过热器入口温度、出口温度的数据进行校正,将过热器出口蒸汽温度在延时时刻前的数据进行稳态处理,再进行数据预处理。减温器出口蒸汽温度和高温过热器出口蒸汽温度处理前后的辨识结果如图5所示。从图5可见:出口温度数据处理前后过热器具有非线性、慢时变、大惯性等特点,直接辨识模型的阶数难度较大,而且会降低辨识精度。其中,动态参数αd在50%负荷下取9.24,在100%负荷下取10.614[20]。由于本文研究的负荷范围为65%~100%,由式(3)中模型阶次表达式可得过热器模型阶次为5。辨识模型结构选择式(4),粒子群算法参数设置基本不变,其中K∈[0,100],T∈[0,300],辨识结果如表2所示。从表2可见:K和T随着负荷增大而减小,随着负荷增加,主蒸汽质量流变大,高温过热器进口蒸汽温度较出口蒸汽温升缓慢,进、出口蒸汽比热容比值变小,根据式(3)可知,K和T随负荷增加而减小,与辨识结果一致。3种工况的适应度都在0.200 0以下,且随着负荷增加模型误差减小,说明机组的负荷越高,系统热工特性越敏感,更容易被辨识。
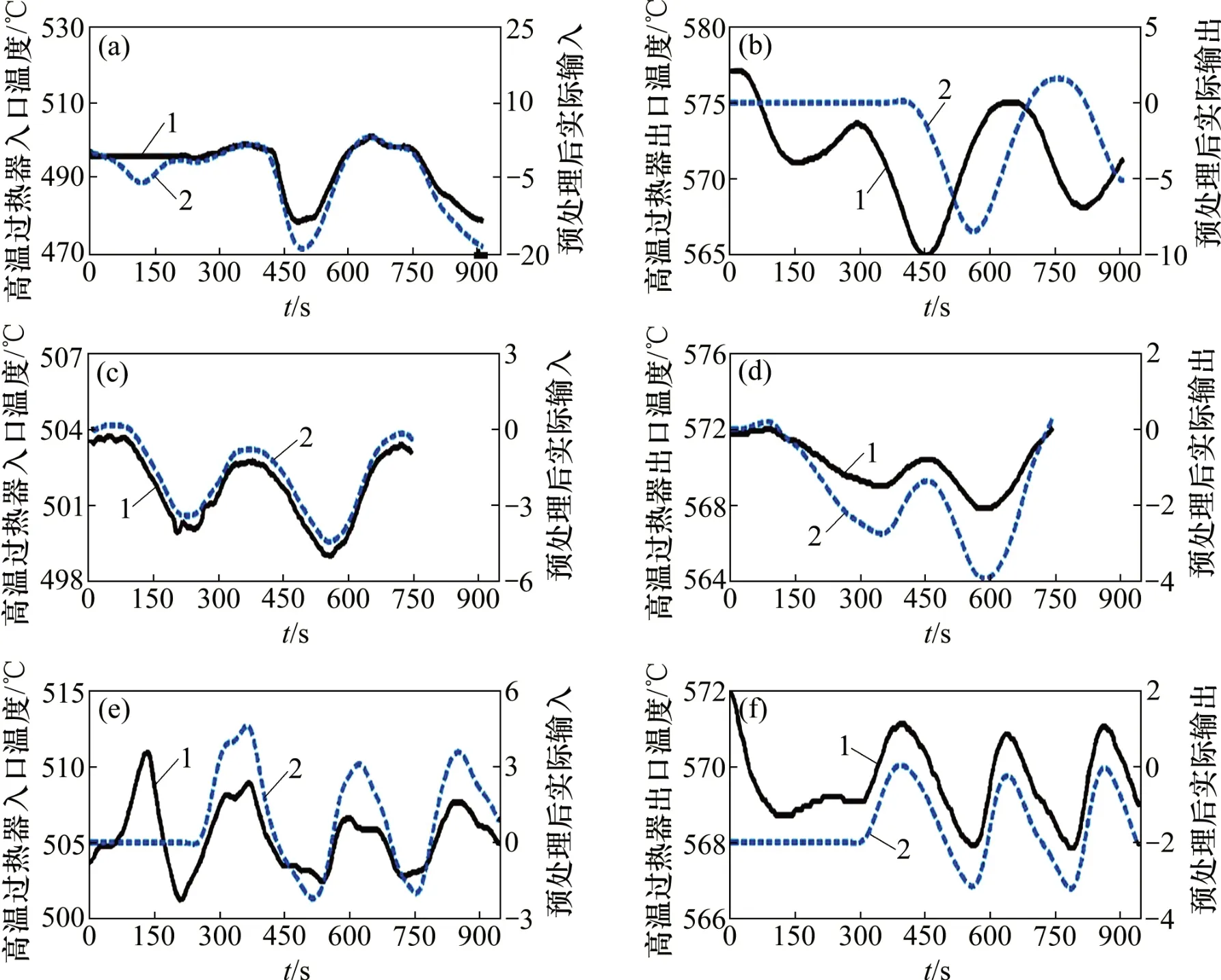
图5 3种工况过热器模型的辨识数据Fig.5 Identification data of superheater model under three operating conditions
图6所示为3 种工况下过热器模型验证结果。从图6可见:过热器入口温度作为激励信号,模型输出结果与实测结果相比,整体上吻合度较高。由于过热器出口蒸汽温度受进口温度与热流量的影响,而在稳态时热流量基本不变,因此,过热器出口温度仅与过热器入口温度相关,两者变化趋势基本一致且具有迟滞性。3种工况模型与其相应运行数据间的最大相对偏差量分别为0.22%,0.18%和0.15%,模型精度较高。在峰值附近(如65%负荷工况下迟滞750 s),仿真结果与实测结果出现较大偏差。这是因为此时蒸汽温度状态是由升温转变为降温,机组其他参数变化较大,激励信号较小的波动被干扰因素覆盖。
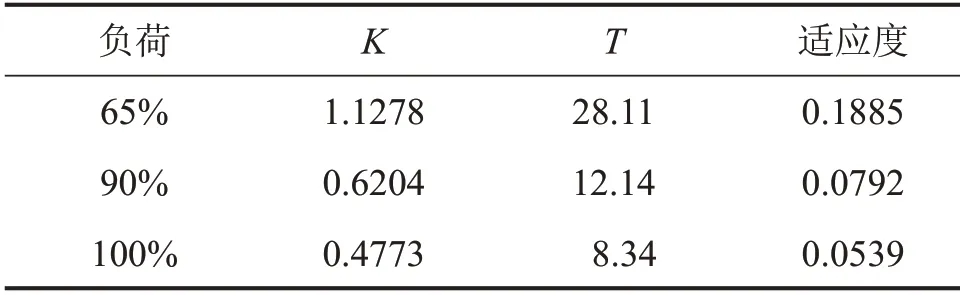
表2 不同工况下过热器模型辨识结果Table2 Superheater model identification results under different working conditions
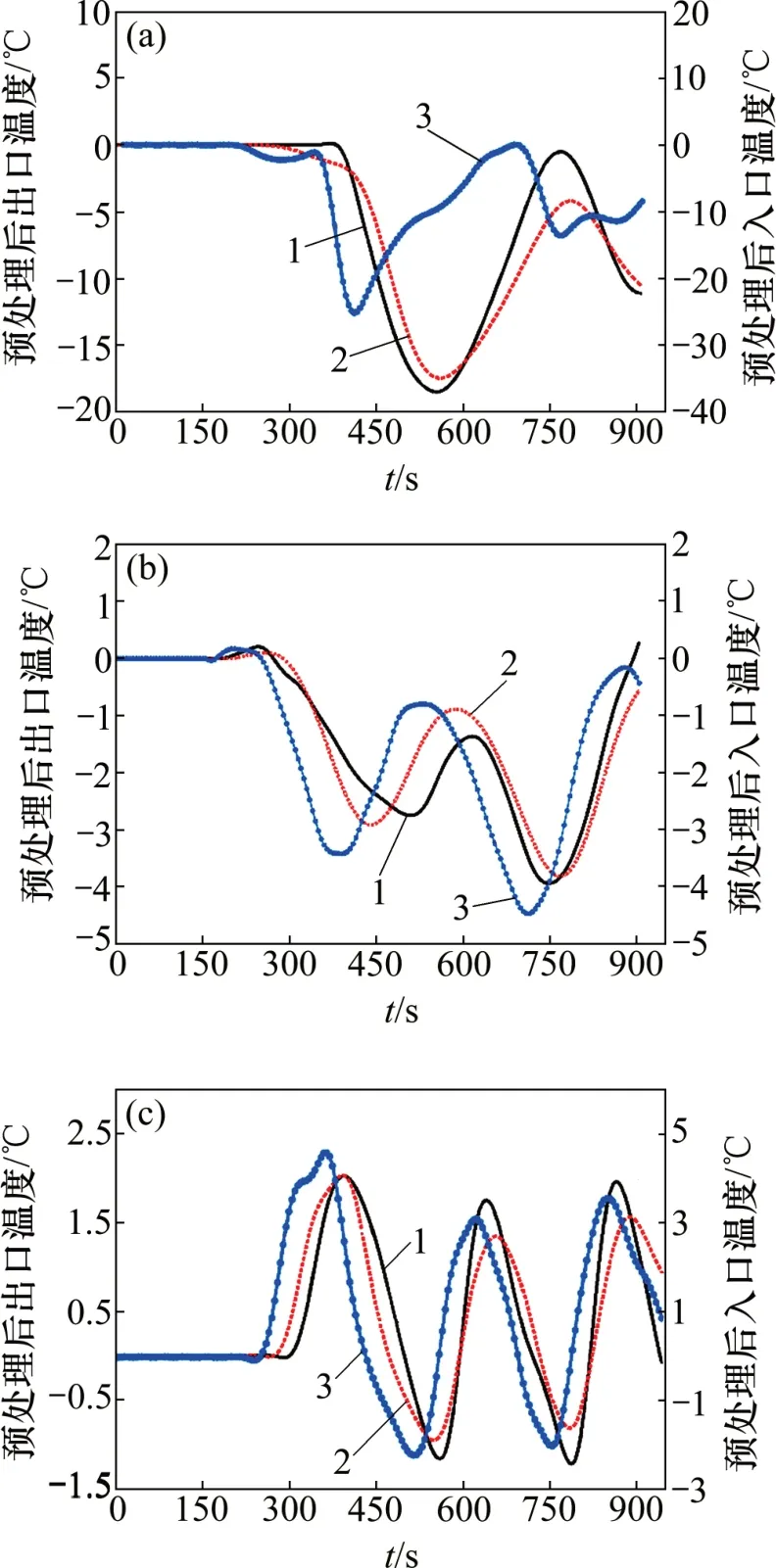
图6 3种工况下过热器辨识模型的验证Fig.6 Verification diagram of superheater model under three working conditions
3 结论
1)基于质量平衡、能量平衡及相关传热方程,建立超临界直流锅炉中减温器、高温过热器传递函数模型;利用粒子群算法辨识现场数据得到3种典型工况下传递函数的具体参数。
2)应用机理建模与寻优算法相结合的方法,建立的末级过热器系统模型精度较高,模型输出结果与实测结果整体吻合度较高。
3)为提高系统辨识的准确度,利用五点三次平滑算法滤波、剔除粗大值、零值化等方法对减温水量和出口温度、过热器出口温度进行预处理,使其具有零初始值并消除噪声;采用灰色关联分析法,可获得不同负荷条件下过热器出口温度对系统输入的迟滞时间。
4)减温器出口温度随减温水流量变大而降低,两者不存在迟滞性;过热器出口温度与过热器入口温度变化趋势一致且具有迟滞性。过热器模型辨识误差比减温器模型的辨识误差大,说明系统响应时间会影响模型辨识的精度。
