溶液预冻方式与冰晶粒度分布之间的关系

贾颖姣，余云霞，刘志强，罗春

(1.中南大学能源科学与工程学院，湖南长沙，410083；2.新奥泛能网络科技有限公司，北京，100176)

真空冷冻干燥是一种稳定的干燥过程。其原理如下：通过低温冷冻使液态水冻结为固态冰，在一定的真空度下，固态水可以直接变为水蒸气，在真空环境中相应的温度和气压下对物料进行冷冻干燥处理。通过真空冷冻干燥得到的产品具有复水性好、稳定性高以及方便运输、能长期保存等优点，因此，广泛应用于真空冷冻干燥技术广泛应用于医药、食品、材料等领域，但由于该技术存在干燥时间长、能耗大等缺点，因而其推广受到限制。为了减少干燥时间，降低操作成本，得到高质量的冻干产品，必须对最佳冻干工艺条件进行研究[1-5]，但所需试验量大、成本高，且结果对整个过程的优化缺乏预测性。从机理方面，冻干过程中升华干燥阶段耗时最长，而预冻阶段影响冻结体的结晶情况即干燥阶段的孔隙结构，对冻干过程产生决定性影响。NAKAGAWA 等[6-8]通过模拟得到了冻干速率和成核温度对冰晶尺寸等参数的影响；贾颖姣等[9]针对液态物料提出了3 种冻结方式，并得出了不同冻结方式对预冻溶液冰晶粒度分布规律的影响。为了提高冻干效率，需要定量地得出不同冻结方式下形成冰晶粒度的分布情况，以及不同冰晶粒度对冻干速率、能耗和复水性等参数的影响，从而获得冻结条件与冻干效率和产品质量的对应情况，再通过逆向推理从机理上求得最佳冻干曲线。为此，本文作者基于数值模拟针对不同冻结方式与结晶粒度平均值和均匀度之间的函数关系进行研究，以便根据冻结方式预测其粒度分布，并根据干燥阶段的需要来调控预冻条件，为研究冻干过程中预冻阶段和干燥过程之间的关系提供依据。

1 数值模拟

1.1 物理模型

基于冻干箱内搁板冻结的预冻方式，以冻干机中2 块搁板间1 个西林瓶内溶液和它所分配的周围空间作为研究对象，忽略西林瓶液面以上的瓶身和瓶口部分对换热造成的影响。简化后的物理模型如图1所示。

1.2 数学模型

图1 西林瓶装物料预冻模型示意图Fig.1 Schematic diagram of freezing material model in vial

在溶液的冻结过程中，固液相变界面随着时间的变化而移动，称为三维两相stefan 问题[10-13]。针对该物理模型进行如下假设：1)只发生热传递，忽略质传递，且传热方式为导热，忽略热辐射和热对流；2)忽略固相和液相的密度差异性，即冷冻前后溶液体积不变；3)冻结过程只发生在固液相界面上，其温度在固化温度和液化温度之间，瓶内冰晶为异质成核，不存在过冷情况；4)冻结区域和液相区域各自分布均匀且内部各处物性分别一致，忽略包含的不凝性气体；5)预冻后只有晶态，没有形成玻璃态物质。针对相变潜热的问题，采取多孔-焓法[14-16]来解决，其中，液相的体积分数由热焓平衡法[17]通过计算得出。能量方程如下：

式中：ρ为材料密度，kg/m3；k为导热系数，W/(m2⋅K)；T为物料温度，K；H为材料的焓，J。H由显焓h和潜热ΔH之和所得：

其中：href为参考焓，J/kg；Tref为参考温度，K；比定压热容cp定义为

式中：cp-s和cp-l分别为固相和液相的比定压热容，J/(kg∙K)；Tsolidus和Tliquidus分别为固化温度和液化温度，K，糊化区域的温度介于这两者之间。

已释放的潜热ΔH为溶液单位潜热L的函数：

其中：ΔH在0～L之间变化；β为液相质量分数，

边界条件为：

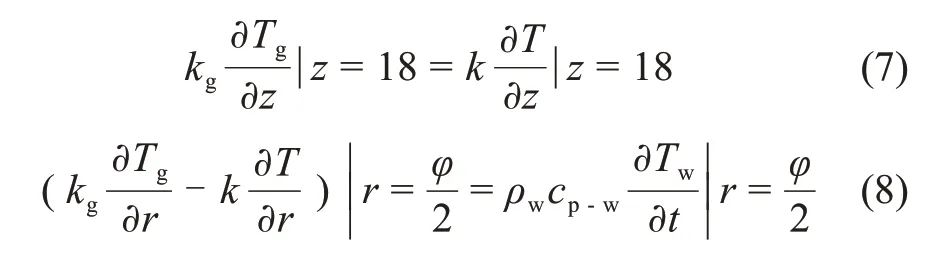
式中：kg为空气导热系数，W/(m2⋅K)；ρw为西林瓶壁材料的密度，kg/m3；cp-w为西林瓶壁的比定压热容，J/(kg⋅K)；Tw为西林瓶壁的温度，K；Tg为空气侧的温度，K。

1.3 数值解法

运用Ansys ICEM 软件建模并划分网格，且进行网格无关性验证[9]。导入Ansys Fluent 15.0 软件，选取凝固和熔化(融化)模型，采用有限体积法的二阶迎风格式对控制方程进行空间离散化，残差设置为10-6，运用SIMPLE 算法对模型温度进行求解。将所得温度场变化的数据导入Matlab软件计算冰晶粒度，并针对该方法进行模型验证[9]。粒晶颗粒粒度计算公式[6]为

式中：D为冰晶颗粒粒度，μm；c为常数；R为相界面的移动速率，mm/s；G为冻结区域的温度梯度，K/mm；R和G为通过处理数值计算结果即温度场间接得到，详细计算过程见文献[9]。

关于冰晶粒度的分布，本文选择平均值和标准差2个参数进行研究，计算式如下：

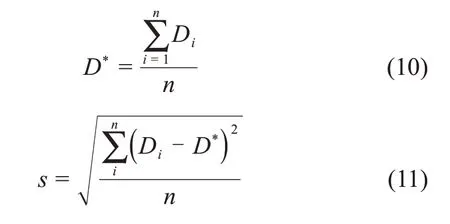
式中：D*为西林瓶中冰晶粒度平均值，μm；n为参考冰晶粒度的位置个数；s为冰晶粒度分布标准差，μm。

1.4 计算参数

1.4.1 几何模型

甘露醇学名为己六醇，常被用作冻干药品的低温保护剂和赋形剂[5,18-19]。本文选取体积分数为10%甘露醇为研究对象，其对应图1中的几何尺寸如表1所示。

表1 几何模型尺寸Table1 Geometric model mm

1.4.2 模拟工况

选取搁板温度作为预冻过程中的控制变量，分别采用以下3组不同的冻结方式：1)将常温物料放入温度恒定的搁板上进行预冻(以下简称恒温条件)；2)先将物料放入常温冻干箱内，然后控制搁板温度以一定速率下降直至冻结(以下简称恒温降条件)；3)先使搁板温度由常温按照一定的速度下降至养晶温度Tm并维持一段时间，而后继续以同样的速度降温(以下简称混养晶条件)。具体模拟工况如表2所示，这3种冻结方式都在常压环境下进行。

表2 3种不同冻结方式下的模拟工况Table2 Simulation conditions of three different freezing modes

2 关系式回归研究

2.1 恒温预冻方式

在恒温冻结方式下，模拟得出各设定温度下冰晶粒度的平均值和标准差，结果如图2所示。为了明确搁板温度与平均粒度和标准差之间的关系，进行多项式回归拟合，拟合的多项式为

式中：A0，A1，…，Ap分别为该函数中的待定系数；p为待定系数个数；ϕ(x)为拟合得出的冰晶粒度分布参数，即平均值或标准差；x为自变量，即搁板温度。

图2 恒温预冻方式拟合曲线Fig.2 Fitting curves in constant temperature condition

令

式中：yi为真实的冰晶粒度分布参数；δi为残量，表示拟合的误差。按照最小二乘法准则[20]确定系数Ai，即求得使残量ϕi平方和最小的Ai。平方和S为

式中：S为残量平方和。

联立并求解式(10)和(12)便可求得拟合多项式。分析对比2 次、3 次和4 次多项式的不确定度，选择最佳拟合多项式，可得搁板温度-平均粒度的拟合多项式为

式中：D*1为搁板恒温冻结方式下拟合得到的冰晶粒度平均值，μm；Tb为搁板恒定温度，K。

所得搁板温度-标准差多项式为

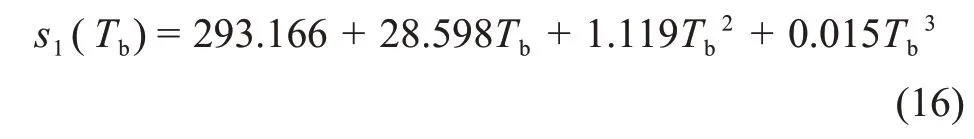
式中：s1为搁板恒温冻结方式下得到的冰晶粒度分布标准差，μm。搁板温度-平均粒度拟合曲线与搁板温度-标准差拟合曲线如图2所示。

2.2 恒温降预冻方式

在恒温降条件下，模拟各设定温降速率条件下冰晶粒度的平均值和标准差，结果如图3所示。根据同样步骤进行多项式拟合，通过不确定度选择最佳拟合多项式，得温降速率-平均粒度的拟合多项式为

式中：D*2为恒温降冻结方式下拟合得到的冰晶粒度平均值，μm；v为搁板降温速率，K/s。所得的温降速率-标准差拟合多项式为

式中：s2为恒温降预冻结方式下拟合得到的冰晶粒度分布标准差，μm。

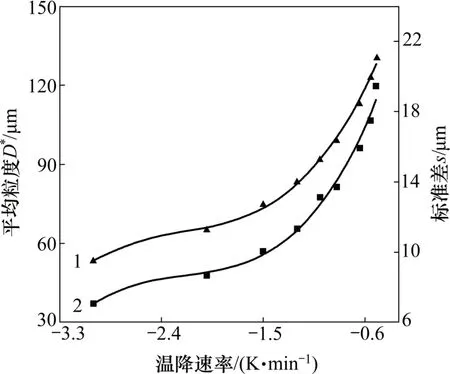
图3 恒温降预冻方式拟合曲线Fig.3 Fitting curves in constant temperature condition drop

2.3 混养晶预冻方式

在混养晶条件下，模拟出各设定养晶温度条件下冰晶粒度的平均值和标准差，结果如图4所示，可得45 min为粒度分布最均匀的养晶时间。

采用同样步骤进行多项式拟合，通过不确定度选择最佳拟合多项式，得养晶时间-平均粒度的拟合多项式为

式中：D*3为混养晶预冻方式下拟合得到的冰晶粒度平均值，μm；t为养晶时间，s。所得的养晶时间-标准差拟合多项式为

式中：s3为混养晶预冻方式下拟合得到的冰晶粒度分布标准差，μm。

图4 混养晶预冻方式拟合曲线Fig.4 Fitting curves in crystal growing condition

3 模型检验和不确定度分析

3.1 多项式模型的有效检验

为了检验冰晶粒度和冻结条件之间确实存在多项式关系，需要进行显著性检验，根据多元统计理论，若取Xl=xl，则实际模型的一元多项式非线性回归问题可简化为多元线性回归问题。可根据多元线性回归的显著性检验统计量检验多项式回归方程的显著性。

假设H0：A1=0，A2=0，…，Aj=0。

检验统计量：

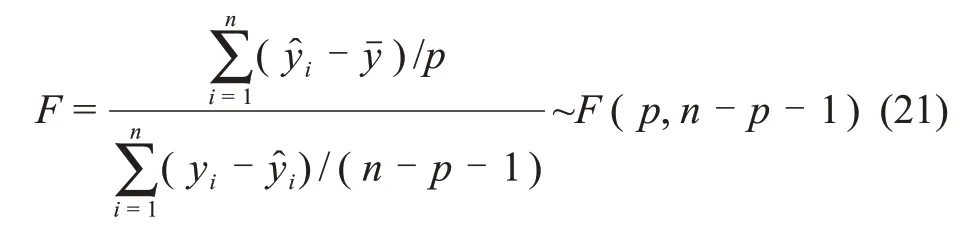
式中：F为检验统计量；为由拟合曲线计算的粒径，μm；yi为由仿真得到的粒径，μm；为yi的平均值；p为变量的自由度，它与拟合多项式的阶数有关，对于多种冻结方式，分别取3，2和4。

若F＞F1-α(p,n-p-1)，则拒绝H0，所得多项式分布在置信水平α上是显著的。所得结果如表3所示。

3.2 不确定度分析

从3种冻结方式的拟合曲线可以看出，拟合结果与原始结果比较接近，拟合效果较好。

3.2.1 均方根误差

均方根误差用来衡量预测值与原始值之间的误差，在一定程度上反映了所得回归公式的效果。残量平方和为

均方根误差为

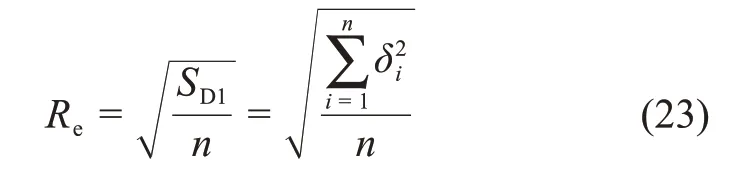
式中：SD1为残差平方和；δi为拟合误差，μm。

3.2.2 校正决定系数

虽然均方根误差可以对拟合进行定量判断，但均方根误差也存在一定局限。为了获得最佳的拟合优度，参考校正决定系数，其值在0～1之间变化，当校正决定系数接近1时，表明拟合效果好。

决定系数R为

校正决定系数Ra为

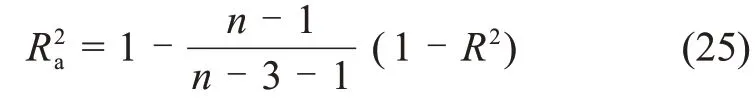
3.2.3 回归参数标准偏差

标准偏差是用来评定回归参数的准确度的量。标准偏差越小，则所得参数越准确。

残余标准偏差se为

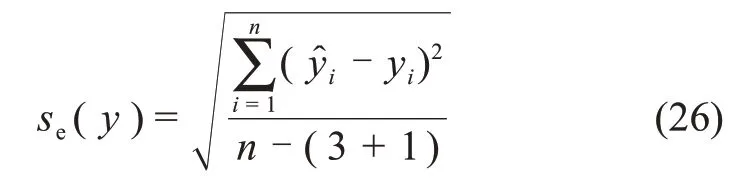
各参数标准偏差se(Ai)(i=1,2,3,4)为

其中：E=B-1；B为求解待定系数Ai的系数矩阵。具体求解过程见文献[20]；Eii为矩阵E中对应的数值。所得结果如表4所示。

表3 不同预冻条件下拟合多项式显著性检验Table3 Significance test of fitting polynomial under different pre-freezing conditions

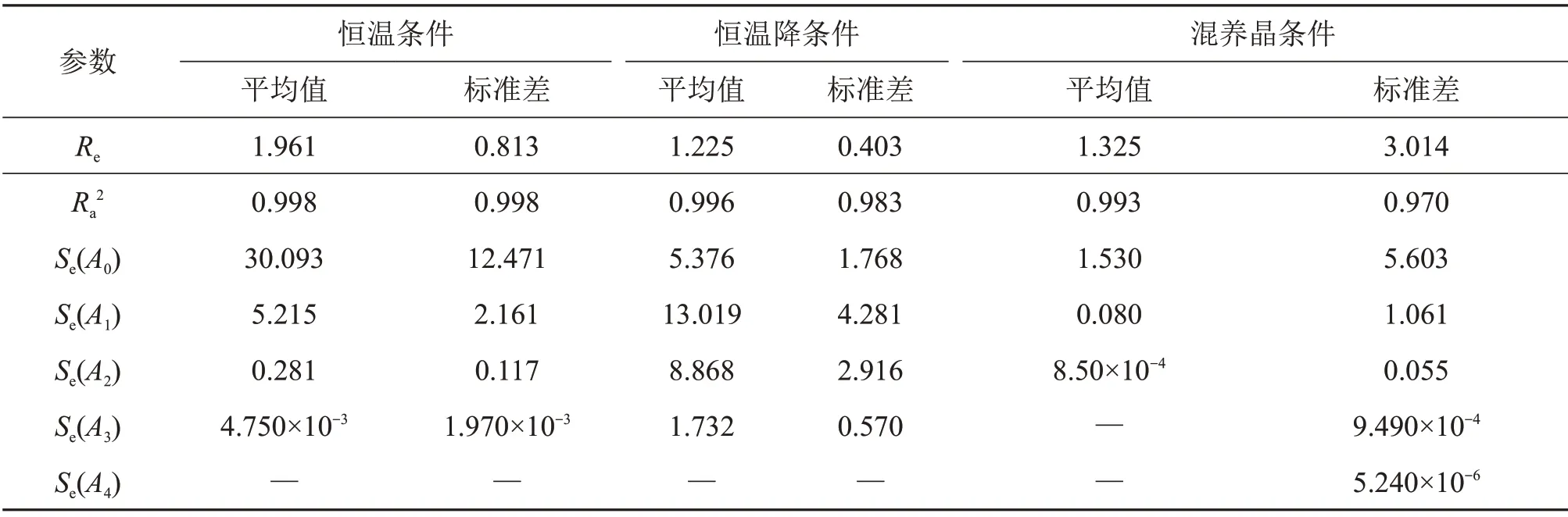
表4 不同预冻条件下拟合多项式的不确定度Table4 Uncertainties of fitting polynomials under different pre-freezing conditions

4 结论

1)在搁板温度恒定的冻结方式下，搁板温度-平均粒径与搁板温度-标准差之间的回归关系式均为三次项式；在降温速率恒定的冻结方式下，温降温度-平均粒径与温降速率回归关系式均为三次多项式。而在含养晶过程的恒温降过程中，养晶时间-平均粒径关系式为二次多项式，而养晶时间-标准差关系式为四次多项式。

2)拟合优度和参数准确度比较高，而且多项式分布显著性水平在0.99以上。

3)后续研究可根据结果推算到其他预冻条件下的冰晶粒度分布情况，定量研究预冻条件对冻干效率和产品质量的影响，优化冻干曲线。