全长黏结GFRP抗浮锚杆拉拔特性分析

白晓宇，张明义，匡政，王永洪，闫楠

(1.青岛理工大学土木工程学院，山东青岛，266033；2.青岛大学环境科学与工程学院，山东青岛，266071)

锚杆具有单点受力小、施工简便、成本低等优点[1-3]，因此，被越来越多地应用于解决建(构)筑物施工过程中的基坑支护、基础底板抗浮等问题。抗浮锚杆就是用于处理底板抗浮问题的一类锚杆。由于地下水位的不确定性以及地下水中包含的各种腐蚀性离子，在一些特殊的工程中还存在杂散电流，抗浮锚杆的工作环境较其他类型锚杆的工作环境更加恶劣。传统钢锚杆的耐久性较差，因此，新型抗腐蚀性抗浮锚杆的研发与推广成为必然[4-6]。玻璃纤维增强聚合物(简称GFRP)锚杆具有良好的抗腐蚀性[7-8]，受到了人们的广泛关注。目前，GFRP 锚杆多应用于基坑[9]、边坡[10]、隧道[11]、桥梁[12]及混凝土加固[13]中，较少作为抗浮锚杆使用。人们对GFRP筋及锚杆的力学性能进行了一系列研究。郝庆多等[14]通过对GFRP筋进行拉拔试验，研究了不同变量下GFRP筋与混凝土之间的黏结强度。刘颖浩等[15]通过改进的拉拔试验，研究了全螺纹GFRP 锚杆在锚固工程中握裹力和黏结特性，并推导出GFRP 锚杆的承载力设计公式，给出GFRP锚杆锚固的设计参数确定方法。ZOU等[16]设计出一种可以固定在GFRP 锚杆外表面的螺旋叶片装置，通过旋转螺旋叶片将GFRP锚杆送入岩层中，其研究结果表明该装置用于GFRP 锚杆是可行的。GONILHA 等[17]通过数值仿真的方法研究了GFRP 筋的拉拔特性，并提出了一种线弹性破坏机制。匡政等[18-19]通过GFRP 抗浮锚杆现场拉拔破坏性试验，将植入式裸光纤光栅传感技术应用于抗浮锚杆拉拔试验中，研究了全长黏结GFRP抗浮锚杆在各级荷载作用下的承载特性、荷载传递特征及破坏机制，同时对GFRP锚杆的蠕变性能进行了研究。抗浮锚杆的数值仿真主要是利用计算机软件模拟锚杆的特定工作环境，分析锚杆在此类工况下的力学特性。数值仿真的方法与试验研究互为补充，有助于更加深入地研究GFRP抗浮锚杆力学与锚固特性。MOHAMED等[20-24]利用数值模拟方法对GFRP锚杆的各类力学性质进行了研究，但多为单一的锚杆拉拔试验。为此，本文作者通过非线性有限元软件ABAQUS，采用Cohesive黏结单元模拟锚杆杆体-灌浆体界面、灌浆体-周围岩体界面之间的接触，建立GFRP 抗浮锚杆杆体-基岩的轴对称数值计算模型，分析长黏结GFRP抗浮锚杆的拉拔特征和变形规律；在此基础上，分析锚杆材料和锚固长度等因素对GFRP抗浮锚杆荷载传递特性的影响，以期为GFRP抗浮锚杆的理论研究和应用提供参考。

1 数值模拟过程

1.1 GFRP抗浮锚杆与基岩的拉拔试验

关于全长黏结GFRP抗浮锚杆与基岩的拉拔特性数值计算模型，本文以文献[25]中的中风化花岗岩中全螺纹GFRP 抗浮锚杆的现场足尺拉拔试验为原型。试验场地位于已开挖的土岩组合基坑内，场区内为块状构造的粗粒花岗岩。分别开展3 根GFRP 筋及3 根钢筋抗浮锚杆的拉拔试验，试验锚杆全长锚固在中风化花岗岩中。岩土层的物理力学参数如表1所示，GFRP筋锚杆试验参数见表2。

表1 中风化花岗岩物理力学参数Table1 Physical and mechanical parameters of moderately weathered granite

表2 GFRP筋锚杆试验参数Table2 Test parameters of GFRP anchor

试验时，锚杆孔径为110 mm，孔深3.5 m，锚固介质选用水泥砂浆，强度等级为M30。采用逐级单调加载的方式施加荷载，GFRP筋抗浮锚杆和钢筋抗浮锚杆每级施加的荷载分别为50 kN 和40 kN，加载到破坏为止。试验过程中采用光纤光栅应变传感器测试GFRP筋锚杆的应力，而采用电阻应变片来测量钢筋锚杆的应力。加载装置和试验过程见文献[25]。

1.2 数值计算模型的建立

中风化花岗岩地基中GFRP抗浮锚杆的物理模型见图1(其中P为拉拔荷载)。

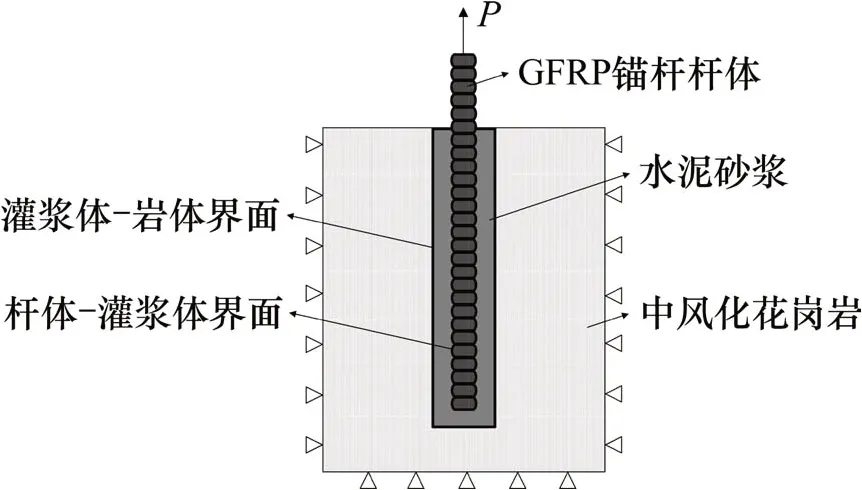
图1 GFRP抗浮锚杆物理模型示意图Fig.1 Diagram of physical model of GFRP anti-floating anchor

由图1可见：GFRP 抗浮锚杆物理模型包括锚杆杆体、水泥砂浆、中风化花岗岩、杆体-灌浆体界面及灌浆体-岩体界面。为了加快分析计算过程，根据物理模型和荷载的对称性，取物理模型中的一半建模，即采用ABAQUS软件建立空间轴对称计算模型，以锚杆横截面形心所在轴线为对称轴。GFRP抗浮锚杆数值模型如图2所示。

图2 GFRP抗浮锚杆数值计算模型Fig.2 Diagram of numerical calculation model of GFRP antifloating anchor

模型中，GFRP锚杆杆体、水泥砂浆及岩体参数与试验参数一致，其中水泥砂浆密度取2.3 g/cm3，弹性模量取20 GPa，泊松比取0.2。为减少网格划分数量，周围岩体的半径取1.5 m。在模拟过程中，将锚杆杆体、水泥砂浆、岩体均简化为各向同性线弹性材料，其中周围岩体的本构模型采用Drucker-Prager 模型(D-P 模型)进行模拟，流应力比取1.0，膨胀角取40°。

在界面属性选择时，杆体-灌浆体界面及灌浆体-岩体界面选用Cohesive 单元层和Maxe 损伤准则，模拟2个界面之间的黏性连接，界面材料的拉伸刚度和剪切刚度均取18 GPa，初始损伤应变取0.000 15。在模拟加载时，把施加在锚杆上的每一级集中荷载等效为均布面荷载，每施加1次荷载设置1个分析步，直至锚杆破坏为止。边界条件的设置与抗浮锚杆的实际工作状态相符，在中风化花岗岩底面及对称轴的一侧分别设置垂直约束和水平约束；因锚杆受力不会引起较远处岩体的变形，因此，在较远处岩体设置水平约束(见图2)。

1.3 网格划分

分配网格属性时，将GFRP锚筋、灌浆体、周围岩体等单元形状设定为四边形，通过结构划分技术来划分网格。单元族选用轴对称应力，将控制属性设定为增强。将Cohesive黏结层单元也设定为四边形，采用扫掠划分网格，扫掠路径可按实际需要选取。为方便网格划分，将装配的整体均划分为四边形区域。网格划分结果如图3所示。网格划分完成后，进行初始地应力平衡模拟。

图3 模型网格划分Fig.3 Grid partition of model

2 模拟结果与分析

2.1 荷载-位移(Q-s)曲线分析

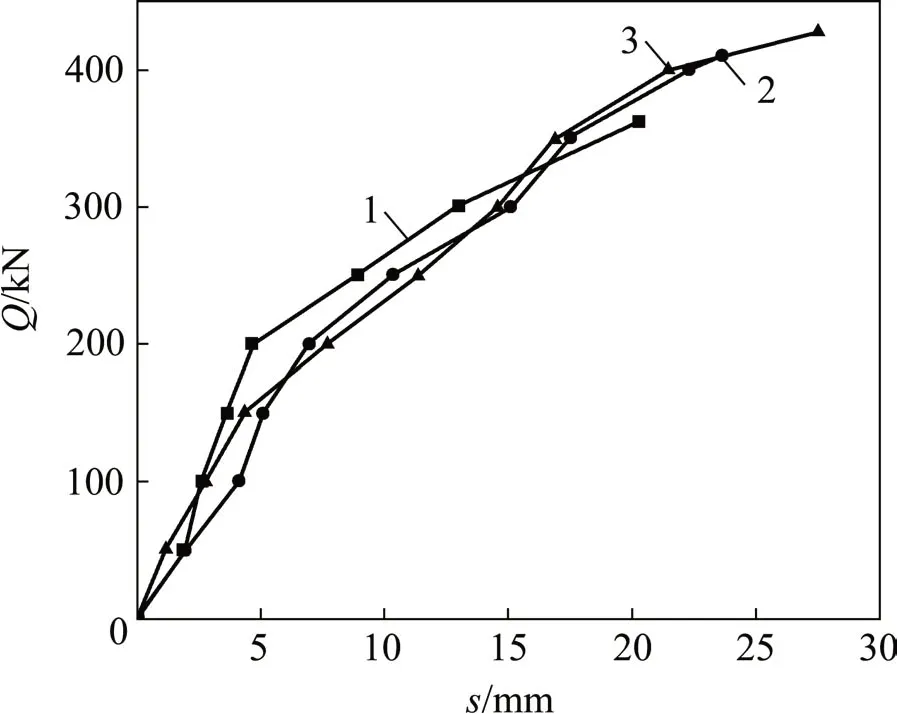
图4 GFRP抗浮锚杆荷载-位移曲线试验结果Fig.4 Experimental result of load-displacement curve of GFRP anti-floating anchor

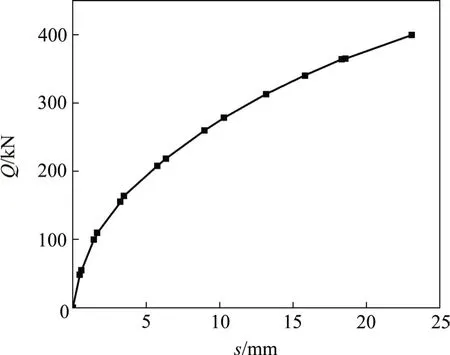
图5 GFRP抗浮锚杆荷载-位移曲线模拟结果Fig.5 Simulational result of load-displacement curve of GFRP anti-floating anchor

GFRP 抗浮锚杆实测得到的荷载-位移(Q-s)曲线和模拟得到的Q-s曲线分别如图4和图5所示。其中，G28-01，G28-02 和G28-03 为GFRP 抗浮锚杆(直径为28 mm)试件编号。从图4和图5可以看出：实测Q-s曲线与模拟得到的Q-s曲线变化规律较吻合。随着荷载的增加，位移基本呈非线性增大趋势。当荷载较低时(不超过150 kN)，实测Q-s曲线基本呈线性变化，GFRP 锚杆发生弹性变形；随后荷载-位移曲线向缓变型过渡，位移随荷载的增加而持续增大。模拟得到的Q-s曲线也呈缓变型，当荷载不高于100 kN 时，模拟得到的Q-s曲线呈线性变化，此时杆体与水泥砂浆界面未发生软化，弹性工作状态明显；随荷载的增大，杆体与水泥砂浆界面出现软化，界面剪切刚度降低，位移逐渐增加。当荷载达到350 kN时，GFRP锚杆的实测位移和模拟得到的位移分别为21.0 mm 和23.2 mm。比较实测Q-s和模拟得到的Q-s这2组曲线可知：数值计算模型中假定的各种材料属性为理想的弹性或塑性，荷载工况也是理想状态，所以模拟得到的Q-s曲线比实测Q-s曲线更平滑。总体来看，数值模拟得到的Q-s曲线变化规律基本可模拟实测的Q-s曲线，说明本文建立的轴对称数值计算模型是合理的。

2.2 轴应力沿锚固深度的分布特征

有限元模拟得到的GFRP抗浮锚杆杆体沿锚固深度的轴应力分布如图6所示。由图6可知：模拟分析得到的轴应力分布规律与文献[25]中的实测结果基本一致。当荷载较低时，轴应力随锚固深度增加呈减小的趋势。以文献[25]中的锚杆G28-03为例，当荷载不超过150 kN 时，轴力沿锚固深度增加衰减为0 Pa，近似呈负指数的分布形式。从图6还可以看出：当荷载不超过200 kN 时，轴应力同样表现出负指数的分布规律；随着荷载的逐渐增大，在孔口以下一定范围内的轴力急剧增加，起初轴力缓慢减小，传递到距地表某一深度后很快衰减为0 Pa。值得注意的是，轴力在特定深度下依然呈负指数分布。当荷载不小于200 kN时，随着荷载的增加，轴应力极大值的分布范围逐渐扩展，在锚固深度0.5 m的位置，轴应力仍以负指数分布规律向下传递，这与文献[25]中实测轴力在荷载不小于150 kN 时的变化规律相符。另外，从荷载传递深度分析，数值模拟得到的荷载传递深度与文献[25]的实测结果基本一致，在锚固深度约3.0 m 的位置，轴应力基本趋于0 Pa，进一步证明了本文模型的合理性。

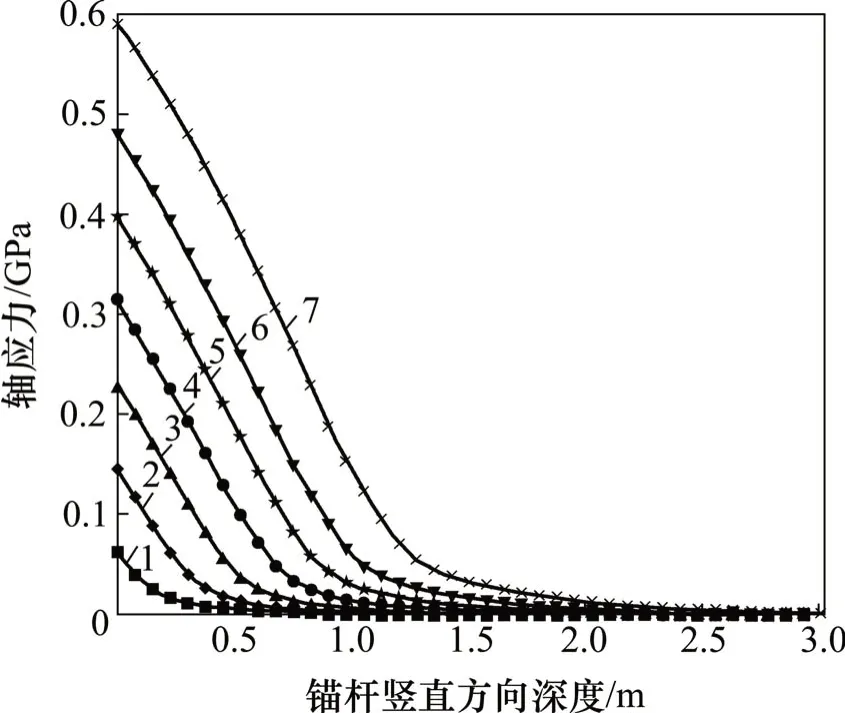
图6 GFRP抗浮锚杆轴应力分布Fig.6 Distribution of axial stress of GFRP anti-floating anchor

2.3 剪应力沿锚固深度的分布特征

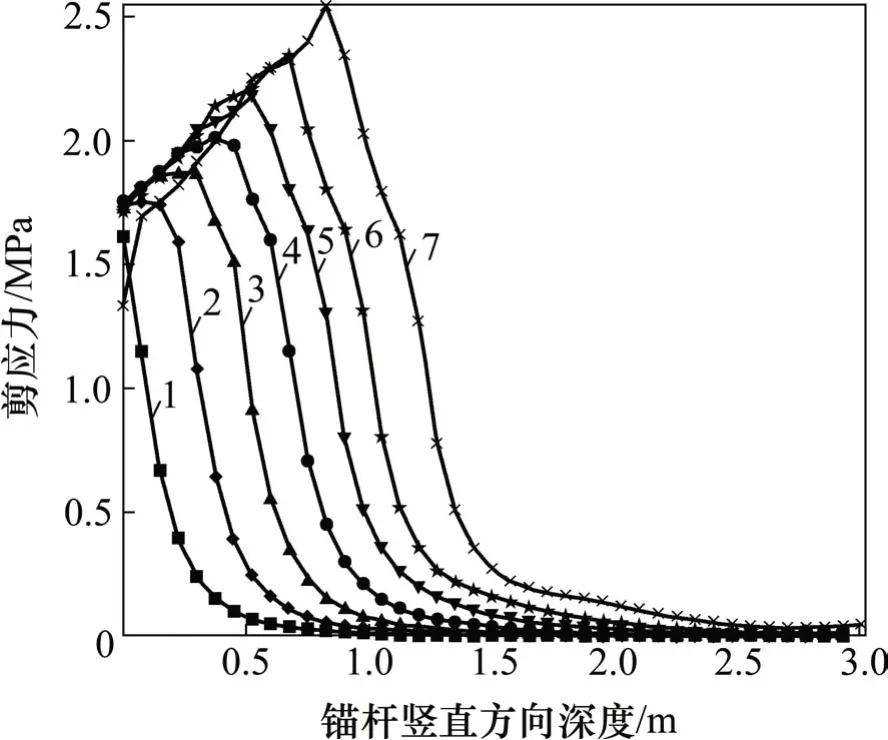
图7 GFRP抗浮锚杆剪应力分布Fig.7 Distribution of shear stress of GFRP anti-floating anchor

有限元模拟得到的GFRP抗浮锚杆杆体沿锚固深度的剪应力分布如图7所示。从图7可以看出：当荷载为50 kN时，杆体与水泥砂浆的剪应力在孔口出现最大值，孔口处杆体-灌浆体界面脱黏；随着荷载的增加，剪应力峰值点沿锚固深度逐渐转移，当荷载达到350 kN 时，在距地表0.8 m 处剪应力达到最大值，约为2.5 MPa。另外，数值模拟得到剪应力沿锚固深度通体分布。而文献[25]中实测得到的剪应力峰值为3.5 MPa，峰值点的位置距地表0.8 m。经比较，有限元模拟得到的剪应力分布规律与尤春安[26]按Mindlin位移解推导出的理论解更接近。这是因为在试验过程中，光纤光栅应变传感器数量有限，实测数据不够充足，而有限元模拟结果更接近剪应力的分布规律。模拟和实测剪应力峰值点位置不同，主要是由于试验过程中剪应力实质上是平均剪应力，即剪应力的位置位于2个相邻光纤光栅应变传感器的中点，因此，实测剪应力峰值位于距地表0.8 m处。此外，模拟得到的最大剪应力与文献[25]中的实测结果相比略小。这主要是因为模型中的灌浆体未考虑其塑性变形；再者，选用的Cohesive黏结单元模拟GFRP锚杆杆体与水泥砂浆界面存在一定误差，只能近似得到剪应力的分布规律。总体来看，模拟分析得到的剪应力分布规律、峰值剪应力的转移、峰值剪应力以及剪应力的分布范围与文献[25]的试验结果较吻合，故可认为本文建立的有限元模型是可行的。

2.4 灌浆体的应力分布特征

由于灌浆体的应力很难在试验条件下获得，不同荷载下灌浆体的应力分布如图8所示。由图8可见：灌浆体的应力随荷载增加而逐渐增大，并沿锚固深度向下传递，灌浆体的锚固作用自上而下逐步发挥。当荷载较低时，在地表附件灌浆体的应力最大；当荷载达到200 kN 时，在距地表0.5～1.0 m 处灌浆体的应力相对较大；当荷载达到350 kN 时，灌浆体的最大应力出现在距地表1.2～1.7 m 处，可见灌浆体应力的分布范围也相应扩大。

图8 不同荷载下灌浆体应力分布Fig.8 Stress distribution for grouting body under different loads

2.5 周围岩体应力与位移分布特征

不同荷载下周围岩体的应力分布如图9所示。由图9可见：周围岩体的应力随荷载的增加而不断增大，并沿锚固深度逐渐向下传递，岩体的嵌固作用与灌浆体类似，自上而下逐步发挥；同时，随着荷载的增加，GFRP抗浮锚杆和灌浆体对周围岩体的横向作用范围也相应增大。当荷载为50 kN时，周围岩体在锚固深度方向的影响深度为0.6 m；当荷载增加至200 kN 时，周围岩体在锚固深度方向的影响深度增加到1.4 m；当荷载增加至350 kN时，周围岩体的影响深度达2.5 m。

当荷载P＝350 kN时，灌浆体周围岩体的应力和竖向位移如图10所示。由图10可见：GFRP 抗浮锚杆对周围岩体的影响半径不超过1.5 m，在锚固深度方向的主要影响范围不超过2.5 m。而周围岩体竖向位移与GFRP 锚杆的位移相比相差5 个数量级，表明对锚杆施加拉拔荷载基本不会引起周围岩体的竖向位移。从图10(b)还可以发现：周围岩体的最大竖向应力发生在距地表约Ld/15(Ld为锚杆的锚固深度)处，这与文献[27]中现场试验得到的结果一致。

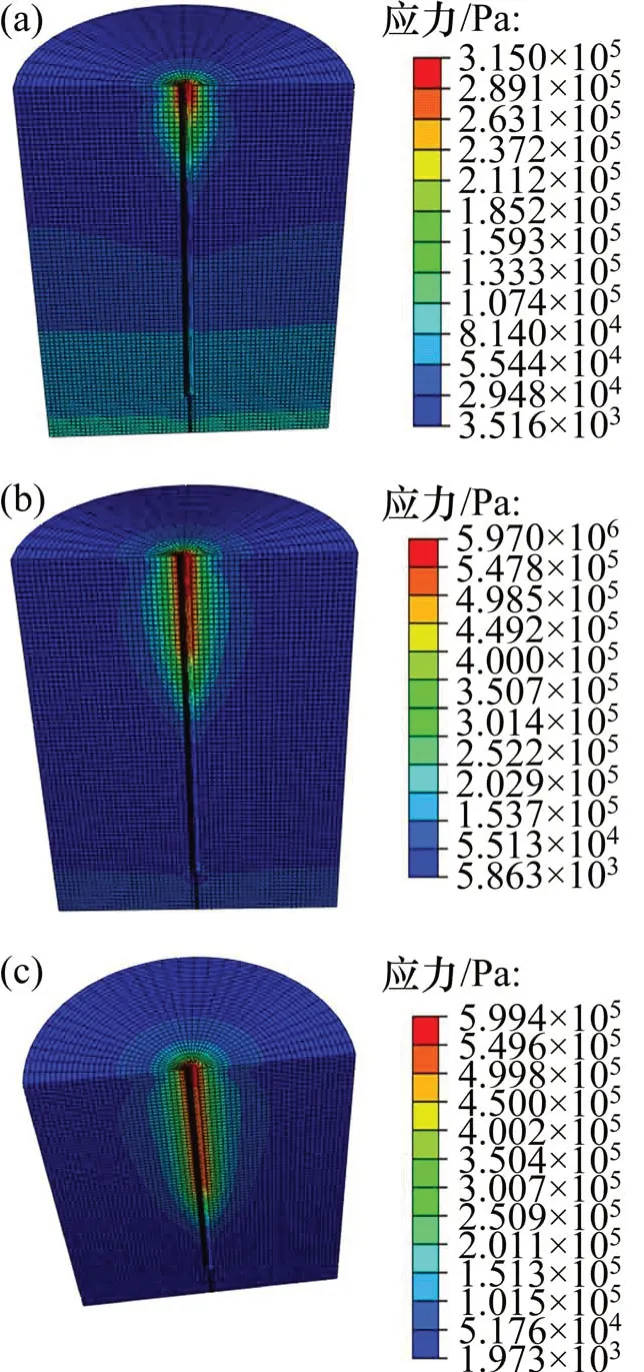
图9 不同荷载下周围岩体应力分布Fig.9 Stress distribution for surrounding rock under different loads

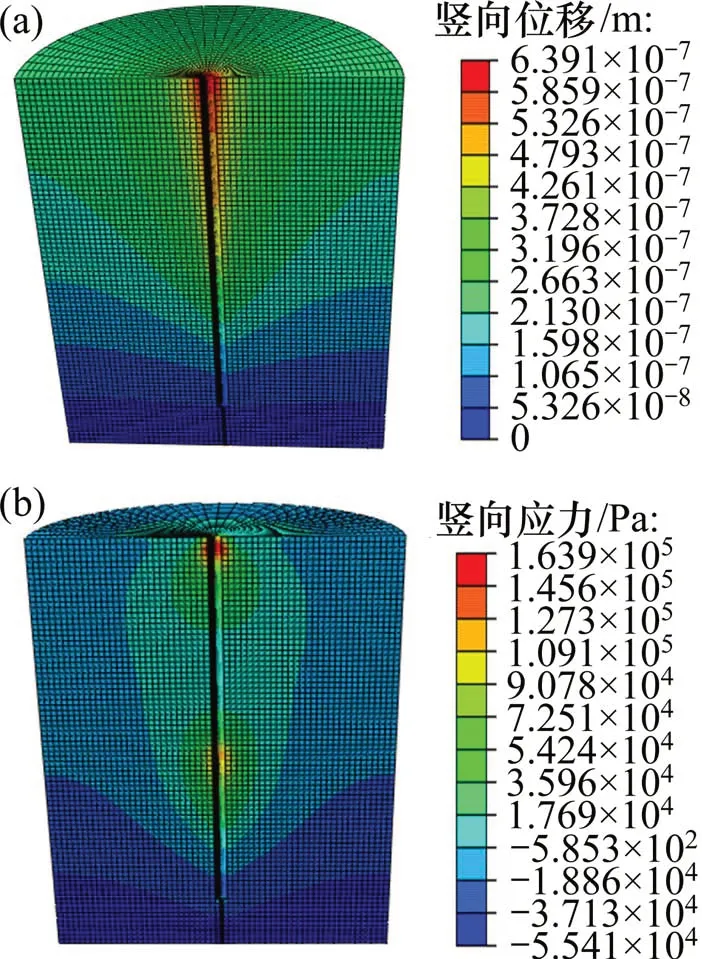
图10 周围岩体竖向应力与位移分布(P＝350 kN)Fig.10 Distributions of vertical stress and displacement of surrounding rock(P＝350 kN)

3 讨论

3.1 钢筋与GFRP筋抗浮锚杆模拟结果比较

为比较不同材质抗浮锚杆的应力分布规律，对相同直径、相同锚固长度、相同水泥砂浆强度等级、相同地层的钢筋抗浮锚杆进行数值建模，同样以文献[25]中的抗浮锚杆为原型建立模型参数。其中，Ш级螺纹钢筋屈服强度为400 MPa，弹性模量为200 GPa，泊松比取0.28。模型建立过程与网格划分流程与GFRP抗浮锚杆的相同。

3.1.1 轴应力分布规律比较

在只改变锚杆材料的条件下，对钢筋及GFRP筋抗浮锚杆进行有限元模拟。以荷载为200 kN 为例，得到钢筋与GFRP筋抗浮锚杆轴应力分布对比如图11所示。

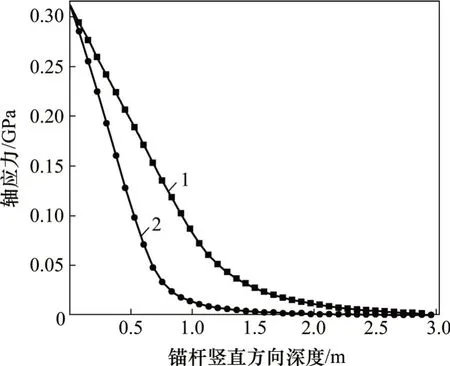
图11 钢筋与GFRP筋抗浮锚杆轴应力分布对比Fig.11 Comparison of axial stress of steel and GFRP antifloating anchor

由图11可知：GFRP筋抗浮锚杆和钢筋抗浮锚杆的轴应力传递深度分别为1.7 m和2.6 m，说明在只改变锚杆材料的条件下，锚筋的弹性模量直接决定轴应力的传递深度。锚筋弹性模量越小，轴应力传递深度越浅。GFRP抗浮锚杆的轴应力影响范围比钢筋锚杆的小，这主要与E/Ea有关(其中，E为岩体的弹性模量，Ea为锚筋的弹性模量)。对于GFRP抗浮锚杆，E/Ea为0.44，而钢筋锚杆E/Ea为0.09，表明E/Ea越小，轴应力沿锚固深度的影响范围就越大，轴应力分布越平缓，这与文献[26]中的研究结果一致。

由于弹性模量的差异性，导致GFRP锚杆轴应力的衰减速率比钢筋抗浮锚杆的快。在距孔口0.13 m以下的区域，钢筋抗浮锚杆的轴应力均比GFRP抗浮锚杆的大；而在加载端，钢筋锚杆的轴应力最大值却比GFRP抗浮锚杆的小。分析其原因，与钢筋的横截面面积相比，直径为28 mm的GFRP筋的横截面面积较小，在荷载相等的条件下，钢筋在加载端的轴应力比GFRP 锚筋的小。另外，GFRP 筋的抗拉强度本身高于Ш级螺纹钢的抗拉强度。

3.1.2 剪应力分布规律比较

为了更加直观地展示钢筋与GFRP筋抗浮锚杆剪应力分布的差异，同样以荷载为200 kN 为例，得到钢筋与GFRP 筋抗浮锚杆剪应力分布对比如图12所示。

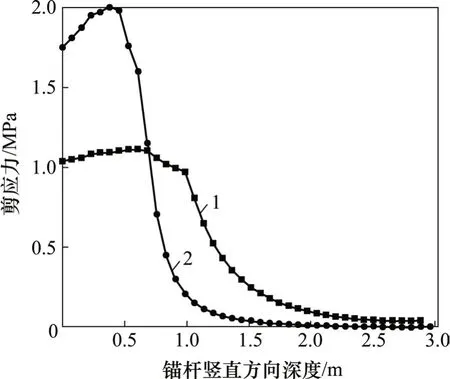
图12 钢筋与GFRP筋抗浮锚杆剪应力分布对比Fig.12 Shear stress comparison of steel and GFRP antifloating anchor

由图12可见：钢筋与GFRP筋抗浮锚杆的剪应力峰值分别出现在距地表0.6 m和0.45 m的位置，剪应力峰值分别为1.1 MPa和2.0 MPa。由于GFRP筋的弹性模量低，所以，杆体-灌浆体界面剪应力更集中，而钢筋锚杆的剪应力分布规律与GFRP锚杆相比更加均匀。就剪应力的传递深度而言，GFRP筋和钢筋抗浮锚杆的传递深度分别为2.0 m和3.0 m，表明锚筋的弹性模量越大，剪应力的影响深度也相应增大。当荷载为200 kN时，2种抗浮锚杆的剪应力均集中于距地表0.5 m 处，可见锚筋弹性模量对剪应力峰值影响显著。

3.2 不同锚固长度GFRP抗浮锚杆应力分布特性

3.2.1 轴应力分布特性对比

在只改变锚固长度的条件下，对锚固长度分别为3.0和5.0 m的GFRP抗浮锚杆进行有限元模拟，得到不同荷载下的轴应力分布，如图13所示。图中，GFRP3 和GFRP5 分别表示锚固长度为3.0 m 和5.0 m的GFRP抗浮锚杆。

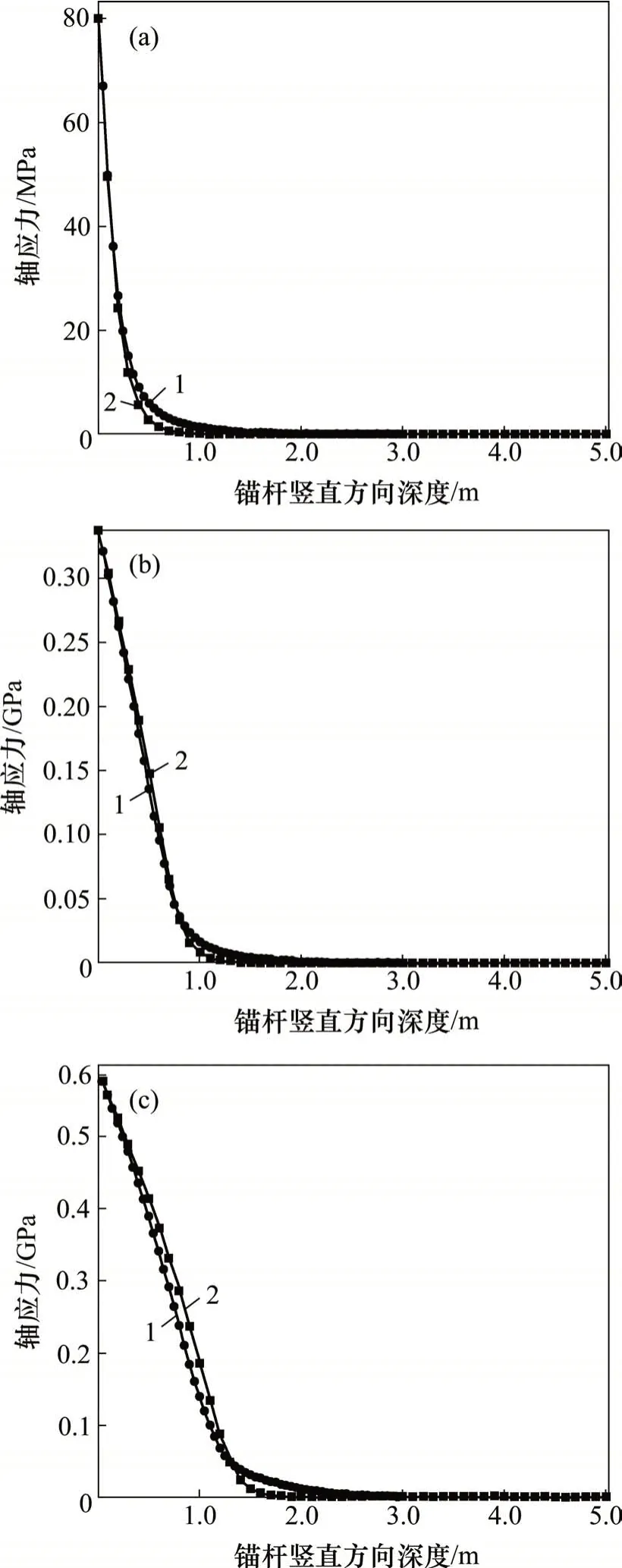
图13 不同荷载下GFRP抗浮锚杆轴应力分布Fig.13 Distribution of axial stress of GFRP anti-floating anchor under different loads

由图13可见：锚杆GFRP3与GFRP5相比，轴应力沿锚固深度方向的衰减慢一些；当P＝50 kN 时，锚杆GFRP3 和GFRP5 在地表位置的轴应力相等；锚杆GFRP3和GFRP5的轴应力传递深度分别为1.5 m和0.9 m，二者均以负指数的分布规律沿锚固深度方向传递轴应力；当P＝200 kN 时，锚杆GFRP5 的传递深度比GFRP3 的小；当P＝350 kN 时，锚固长度对轴应力的影响与P＝50 kN 和P＝200 kN 时的相同。另外，对比图13(b)和(c)可知：锚杆GFRP3的荷载传递范围比锚杆GFRP5 的大，说明在本模拟条件下，锚固长度越长，轴应力传递范围越小；荷载越大，有效锚固长度越长，冗余长度(锚固长度减去有效锚固长度)越短。

3.2.2 剪应力分布特性对比

不同荷载下GFRP抗浮锚杆的剪应力分布如图14所示。从图14可以看出：锚杆GFRP3 的剪应力峰值比锚杆GFRP5 的剪应力峰值出现得更早，即锚杆GFRP3 和锚杆GFRP5 的剪应力峰值相比，锚杆GFRP3 的剪应力峰值更大，且峰值点的位置离地表更近。在荷载相同的情况下，锚杆GFRP3 和GFRP5的剪应力均表现出上述的分布规律；随着荷载的增大，锚杆GFRP3 和GFRP5 剪应力峰值的差距逐渐拉开，剪应力峰值点的距离逐渐增大。当P＝50 kN时，锚杆GFRP3 与GFRP5 的剪应力峰值相差0.06 MPa，峰值点的间距为0.06 m；当P＝200 kN时，二者的剪应力峰值相差0.07 MPa，峰值点的间距为0.09 m；当P＝350 kN时，二者的剪应力峰值相差0.16 MPa，峰值点的间距增加至0.17 m，与P＝50 kN 时相比，剪应力峰值的差值提高167%，峰值点的间距增大183%。

与杆体轴应力分布规律类似，锚杆GFRP3 的剪应力传递深度比锚杆GFRP5 的大，且传递深度的差异随荷载的增加而逐渐增大。当P＝50 kN 时，锚杆GFRP3和GFRP5剪应力的传递深度为1.0 m，二者相差较小；当P＝350 kN 时，锚杆GFRP3 和GFRP5 的剪应力传递深度分别为3.0 m和2.0 m，可见在有效锚固长度内，荷载对不同锚固长度抗浮锚杆的荷载传递深度影响较大。

4 结论

1)通过ABAQUS 非线性有限元软件，采用Cohesive 黏结单元模拟锚杆杆体-灌浆体界面、灌浆体-周围岩体界面之间的接触；本文建立的有限元模型能够较好地反映GFRP抗浮锚杆的荷载-位移关系、轴应力及剪应力沿锚固深度的分布规律，验证了模型的可行性与合理性。

2)随着荷载的增加，灌浆体的应力逐渐增大，并沿锚固深度向下传递，灌浆体应力的影响范围也逐渐扩大，灌浆体的锚固作用自上而下逐步发挥。

3)周围岩体的应力随荷载的增加而不断增大，并沿锚固深度逐渐向下传递；随着荷载的增大，GFRP抗浮锚杆对周围岩体的横向作用范围也相应增大；周围岩体的最大竖向应力发生在距地表约Ld/15(Ld为锚杆的锚固深度)的位置。

4)在只改变锚筋材料的条件下，锚杆轴应力与剪应力的传递深度由锚筋的弹性模量控制，锚筋弹性模量越小，轴应力与剪应力传递深度越浅；GFRP锚杆轴应力的衰减速率要比钢筋抗浮锚杆的快；GFRP抗浮锚杆的轴应力影响范围比钢筋锚杆的小，这取决于E/Ea(E为岩体的弹性模量，Ea为锚筋的弹性模量)。锚筋弹性模量对锚筋-灌浆体界面剪应力峰值所处位置并无明显影响，只是对剪应力峰值影响显著。

5)在只改变锚固长度的条件下，GFRP抗浮锚杆的锚固长度越长，轴应力衰减速率越快，轴应力传递范围越小；相应的剪应力峰值点出现得更晚，峰值剪应力越小，传递深度越小，峰值点的位置距地表越远，且剪应力传递深度的差异随荷载的增加而逐渐增大。