各向异性成层边坡的稳定性分析

罗凌晖，周建，蔡露，温晓贵

(1.浙江大学滨海和城市岩土工程研究中心，浙江杭州，310058；2.浙江省城市地下空间开发工程技术研究中心，浙江杭州，310058；3.苏州常宏建筑设计研究院姑苏分公司，江苏苏州，215000)

边坡稳定分析是边坡设计的前提，能有效判断边坡失稳时的推力，为后续支护结构的设计提供依据，从而有效防止因边坡失稳破坏而形成的各种地质灾害(如滑坡、崩塌、泥石流等)，为构筑物的正常使用和人们的生命财产安全保驾护航[1]。常用的边坡稳定分析方法有极限平衡法、极限分析法、滑移线场法、有限元数值分析方法等等。人们分析时往往将边坡土体视为各向同性材料[2-5]，而天然软土由于沉积，初始不等向固结及复杂应力路径等原因呈现出显著的各向异性。ZAREI等[6-11]的研究结果表明：主固结方向土体不排水抗剪强度要比其他方向的高。对于开挖边坡而言，边坡圆弧滑动面上土体单元的大主应力轴方向角是连续变化的，滑动面底部区域土体单元的大主应力轴与竖直方向夹角α甚至可以达到90°，由于各向异性的客观存在，该区域土体强度低于边坡顶部土体强度，如果统一采用三轴压缩不排水抗剪强度指标对土坡进行稳定分析，可能会得到偏高的安全系数。因此，如果不考虑土体各向异性，那么在对岩土工程问题的分析中将无法保证结果的准确性[12-13]。目前，考虑土体强度各向异性的边坡稳定的主要研究方法有传统分析方法和理论分析公式法。传统分析方法首先假设有1 个确定的滑动面。例如，CHEN 等[14]将Casagrand 土体强度各向异性表达式引入极限分析法的上限理论，得出了不同坡度角以及不同各向异性系数条件下的边坡稳定系数；赵红华[15]采用Bishop条分法分析了土体强度各向异性对边坡安全系数的影响，得出土体黏聚力各向异性对边坡稳定性的影响要大于内摩擦角各向异性的影响，且各向异性程度愈大，影响愈强烈等。理论分析公式法仅仅是三轴压缩抗剪强度与三轴拉伸抗剪强度的简单组合，没有考虑到土体实际的力学特性。例如，王栋等[16]以Casagrand 公式为基础开发了能自动搜索边坡安全系数的有限元数值分析方法，并探究了边坡安全系数随各向异性系数的变化规律；SU 等[17]重新建立了以三轴压缩和三轴拉伸抗剪强度为变量的土体强度各向异性表达式，分析了强度各向异性对边坡安全系数的影响。然而，将试验所得土体强度各向异性引入商业有限元软件中从而对各向异性成层边坡进行稳定分析的研究较少。本文作者以杭州软黏土复杂应力路径下不排水抗剪强度试验及屈服特性试验结果为基础，提出考虑土体不排水抗剪强度各向异性的半经验公式，并依据该公式的基本原理提出考虑土体强度各向异性的修正Von-Mises屈服准则；利用商业有限元软件ABAQUS 的UMAT子程序进行二次开发，建立考虑土体强度各向异性成层边坡分析模型；在此基础上，采用强度折减法探究成层边坡土体各向异性和不排水抗剪强度等因素对边坡安全系数的影响，并结合实际算例，验证本文方法的可靠性。

1 各向异性不排水抗剪强度公式推导

关于不排水抗剪强度的研究，大多是通过与沉积面呈不同角度切取土体制作试样，然后，利用这些试样进行常规室内土工试验，如常规三轴、直剪和平面应变试验等。此类试验由于仪器的局限性，无法真正实现主应力轴的旋转[12-13]。为了真正实现土样加载直至破坏过程中主应力轴方向的偏转，沈扬[9]应用空心圆柱扭剪仪(HCA)探究了杭州地区软黏土强度各向异性，发现其不排水抗剪强度各向异性随主应力轴方向呈现“勺型变化”。高彦斌等[10]利用室内异形十字板试验对上海软黏土强度各向异性特征进行了研究，发现试验结果与Casagrande 公式和Carrillo 公式[18]计算结果较吻合。应宏伟等[19]结合Casagrande公式中考虑不排水抗剪强度最小和最大时所对应的α，对文献[9]中的试验结果进行了拟合，得到杭州地区典型软黏土在大主应力方向为α剪切时的不排水抗剪强度Suα为

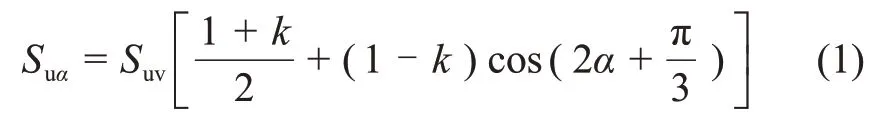
式中：Suv为三轴压缩不排水抗剪强度；α为大主应力轴方向与竖直方向夹角，取值范围为0°～90°；k为各向异性比；根据空心圆柱扭剪仪(HCA)试验中空心土样的双向轴对称特性，α为-90°～0°时对应的Suα可由0°～90°时的Suα对称得到；k取值为α= 90°和α= 0°时不排水抗剪强度的比值。

主应力轴方向常常和破坏面的方向联系在一起，LO[20]的研究结果表明，主应力轴方向与土体剪切破坏面的夹角ψ为常量。

式中：ϕ′为土体的有效内摩擦角。沈扬[9]根据主应力轴方向旋转的不排水抗剪强度试验，发现剪切破坏面与主应力轴方向的夹角随主应力轴方向改变不明显，一般为25°～30°。杭州地区典型软土为全新世最后一次海侵过程中形成的海相沉积土，呈现流塑状态并具有水平层理。王冠英等[21]通过微观电子显微镜对杭州地区典型软土进行定向度测定，发现该土样颗粒薄平表面与沉积面平行的颗粒数约为与沉积面垂直的颗粒数的2 倍。由此可见，当剪切破坏面方向为水平向时，土体颗粒之间最易产生相对滑动。

本文根据上述研究成果以及杭州地区典型软土的微观破坏机理，在α=ϕ′/2 - 45°方向上取不排水抗剪强度为最大值，在α=ϕ′/2 + 45°方向上取为最小值，即土体剪切破坏面为竖直方向和水平方向。根据Casagrande 公式，则有

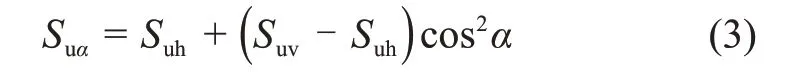
式中：Suh为三轴拉伸不排水抗剪强度。

将式(3)中的大主应力轴方向角转换为剪切方向角可以得到

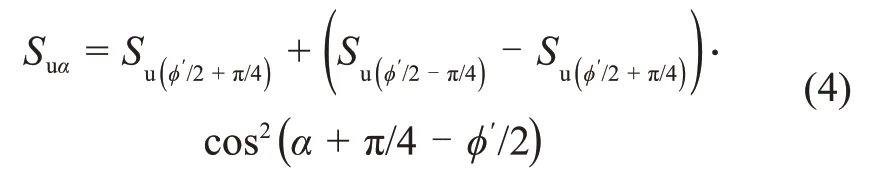
将α= 0°和α= 90°分别代入式(4)整理后可得：

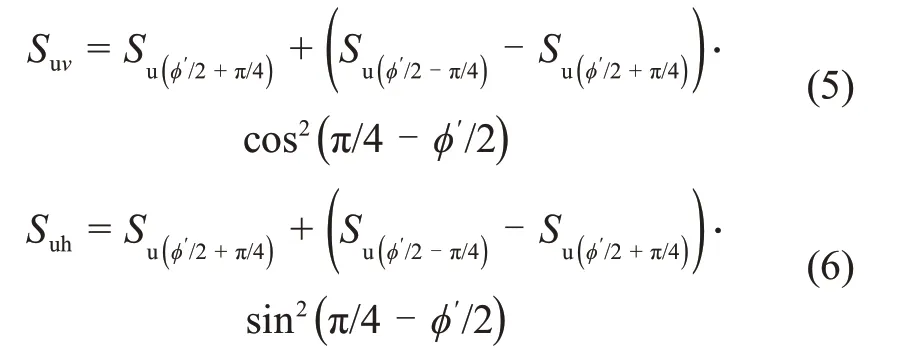
由式(5)和式(6)可得：

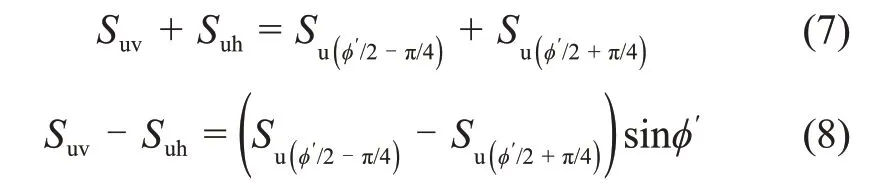
由式(7)和式(8)可得：

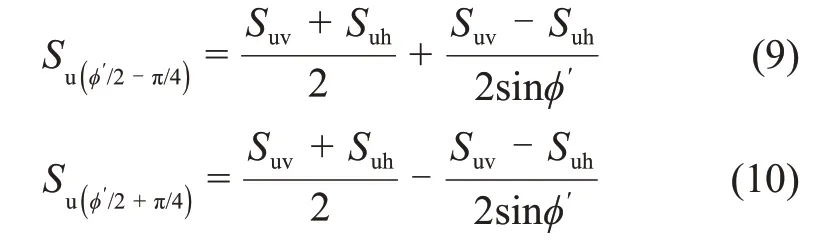
最后，将式(9)和式(10)代入式(4)得到不排水抗剪强度表达式：

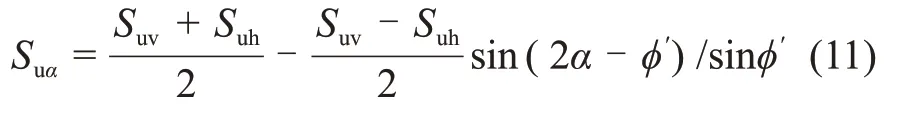
式(11)即为考虑土体有效内摩擦角影响的强度各向异性半经验公式，包含三轴压缩不排水抗剪强度Suv、三轴拉伸不排水抗剪强度Suh以及土体有效内摩擦角ϕ′共3个参数。

为了探究土体各向异性程度对岩土工程问题各种系数的影响，通常将Suh/Suv定义为一个新的变量，但尚未形成一致的表达[16-19]。本文统一将k=Suh/Suv定义为不排水抗剪强度各向异性比，简称为各向异性比。将k代入式(11)可以得到

对比式(1)和式(12)可知：式(1)是式(12)取ϕ′=30°时的一种特殊情况，因此，本文公式适用性更广。图1所示为在不同情况下，大主应力轴方向角-90°≤α≤90°时，归一化不排水抗剪强度Suα/Suv随α的变化情况。图1中，本文公式取有效内摩擦角ϕ′=30°。

由图1可知：本文公式与Casagrande公式的强度各向异性规律具有显著差异，本文公式可以考虑大主应力轴方向角在-90°≤α≤90°范围内的变化规律，最大值并不在α= 0°处，而是在-90°≤α≤0°范围内，这与文献[10]中的试验结果相符。相比于Casagrande 公式，本文公式归一化抗剪强度Suα/Suv在0°≤α≤90°范围内的结果与文献[9-10]中的试验结果拟合度更高，可见本文公式在参数选取合理的前提下具有一定的优势。因此，下面将以式(12)为标准，推导考虑强度各向异性的修正Von-Mises准则。

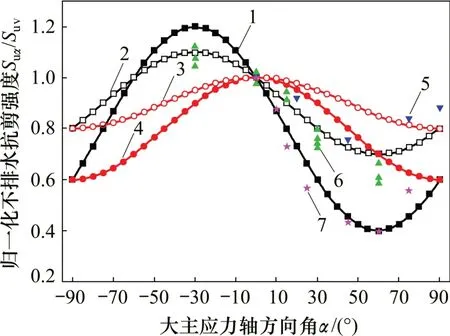
图1 不同公式及试验所得归一化不排水抗剪强度Suα/Suv对比Fig.1 Comparison of normalized undrained shear strength Suα/Suv by different formulas and various test results

2 考虑强度各向异性的修正Von-Mises屈服准则

在工程实践中，对基坑边坡开挖进行不排水数值分析时，通常选用固结不排水抗剪强度指标ccu和ϕcu，按照Mohr-Coulomb 或Drucker-Prager 屈服准则进行分析。对于海底边坡、水库边坡或地下水位较高的基坑开挖边坡，土体主要由软黏土构成且处于饱和状态，渗透系数较小，加荷速率较快。龚晓南等[22-23]认为应选用不排水抗剪强度指标对该类问题进行计算分析。不排水条件下的软黏土力学特性更符合Tresca或Von-Mises 屈服准则。由于在三维主应力空间中Tresca 屈服面有角点存在，在数值分析中会遇到困难，因此，本文采用Von-Mises屈服准则和强度各向异性半经验公式推导考虑强度各向异性的修正Von-Mises屈服准则。

为了计算方便，岩土工程中常用有效主应力组成的应力不变量来表示土体的应力状态。常用的应力不变量包括平均有效应力p′、等效剪应力J和应力罗德角θ。

式中：σ′1，σ′2和σ′3分别为大主应力方向、中主应力方向和小主应力方向的有效正应力。则Tresca准则的屈服函数fT可以用主应力表示为

式中：Su为土体不排水抗剪强度。

Von-Mises 准则的屈服函数fM可以用主应力表示为

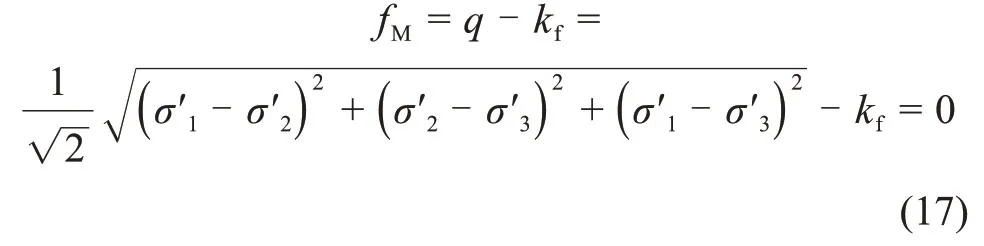
式中：q为等效应力，kf为Von-Mises 准则的屈服强度。将式(16)和(17)用应力不变量表示为：

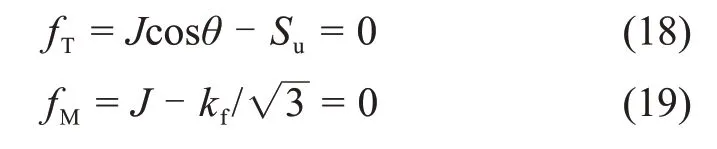
Tresca 准则和Von-Mises 准则的屈服函数在偏应力平面内的形状分别为正六边形和圆形，有2个Von-Mises 圆，其中，一个是Tresca 正六边形的外接圆，另一个是内切圆。一般认为Von-Mises 屈服函数是Tresca 屈服函数的近似形式，因此，需要寻找和Tresca 正六边形拟合最好的圆。由文献[24]可知拟合最好的圆在θ=±15°处，因此，将θ=±15°代入式(18)，联立式(18)和式(19)并取fT=fM，可以得到

为进一步考虑不排水抗剪强度各向异性的影响，将式(20)中的Su和式(12)中的Suα对应起来，将式(12)和式(20)代入式(17)，得到修正的Von-Mises 准则的屈服函数为

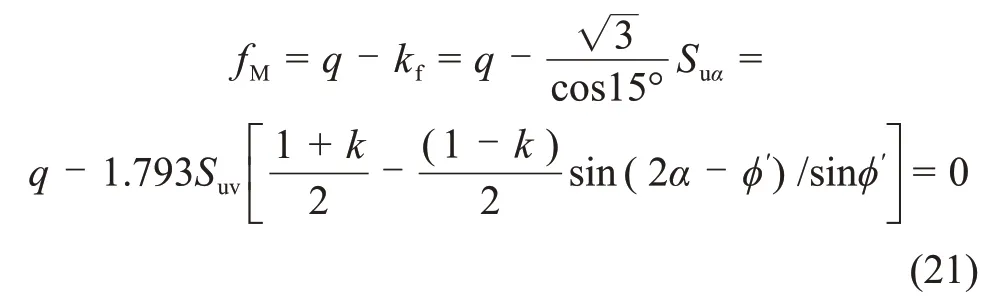
修正的Von-Mises准则仍假定塑性应变增量与塑性势面正交，则土体不会产生塑性体积应变增量，以此来保证模型能准确反映饱和土体的不排水力学特性。

为了完整表达该模型，还需要确定弹性参数。由于不排水剪切过程中不会产生弹性体积应变，取泊松比υ≈0.5，这样，模型中就只剩不排水弹性模量Eu和不排水剪切强度Su需要提前确定。在实际工程应用中，由于土并非理想弹塑性体，其变形包含了可恢复的弹性变形和不可恢复的残余变形2 个部分，因此，在静荷载作用下计算土体变形时常采用压缩模量和变形模量等。本文采用修正的Von-Mises 屈服准则，将土体视为弹性-理想塑性材料，因此，对于不排水弹性模量这一参数应选用土体弹性模量进行计算分析。一般通过室内三轴仪进行不排水三轴压缩试验，根据得到的应力-应变关系曲线确定土的弹性模量。详细的试验方法参见文献[25]。

3 强度折减法有限元模拟

随着计算机应用技术的高速发展，利用有限元强度折减法进行边坡稳定分析受到国内外研究者的广泛关注[26-28]。相较于传统的边坡稳定分析方法如极限平衡法、极限分析法和滑移线场法等，有限元强度折减法不需要事先假定边坡最危险滑动面的形状和位置，只需要不断降低边坡土体的强度参数，进而使边坡土体因抗剪强度不足而发生失稳破坏，就能得到边坡的滑动面形状及相应的安全系数。

目前，对于均质边坡，有限元强度折减法已经取得了较可信的结果。该方法的核心理念如下：在理想弹塑性有限元计算中逐渐降低边坡岩土体抗剪切强度，直到其达到破坏状态为止[4]，此时，得到的强度折减系数即为边坡稳定安全系数F，相关原理可以表示为

式中：c和φ为土体原本的抗剪强度参数；cm和φm为折减后土体实际用于计算的抗剪强度。

根据有限元分析结果判定边坡处于破坏状态，是运用强度折减法求解安全系数的重点。根据目前的研究进展，边坡失稳判据可分为如下3种：1)有限元程序迭代过程中出现力或位移的不收敛，即最终数值计算结果不收敛；2)特征点发生位移突变或具有较大的变形趋势；3)从坡脚到坡顶形成等效塑性应变或广义塑性应变的连续贯通区。

根据文献[28]，将边坡滑动面上所有单元节点中任一节点的塑性应变或位移出现突变且产生较大程度无限制的塑性流动作为边坡失稳的标志。每一折减系数最多允许500次迭代，采用平面应变四边形八节点等参单元(CPE8)对各向异性成层边坡模型进行网格划分。

为了模拟土体强度各向异性，利用ABAQUS 的UMAT子程序编写修正的Von-Mises屈服准则，计算流程如下。

1)体力施加采用分级加载，每一级加载开始时，主程序调用UMAT 子程序的材料信息传入单元积分点，同时传入时间步长、应变增量、荷载增量、当前状态应力和应变以及其他所有求解过程所需要的变量。

2)UMAT 子程序沿着应变增量路径对本构方程进行积分，得到新的应力增量，并同时更新其他相关变量，然后，提供Jacobian矩阵给主程序以计算形成新的整体刚度矩阵。

3)ABAQUS 主程序结合当前加载步的残余荷载和位移增量进行平衡检验，不平衡力和位移增量修正容许的相对误差分别为0.5%和1.0%，若不满足平衡收敛条件，则继续迭代，直至收敛[16]。然后，进行下一加载步计算。

本文采用完全隐式的向后Euler 积分回映算法进行计算。该算法的核心是将增量弹塑性本构方程转化为一组非线性方程组，然后，利用牛顿迭代方法对该非线性方程组进行线性化处理并求解。隐式回退算法因强化了子增量步结束时的一致性，避免了屈服面的漂移，具有较高的精确性。

4 算例验证与讨论

由于很难假定统一的滑动面形式，传统边坡稳定分析方法难以推广到各向异性成层边坡，而有限元方法在计算完成后自动得到滑动面，适用于确定实际工程中广泛存在的复杂成层边坡的安全系数。下面根据文献[29]中的算例，验证本文方法对各向异性成层边坡进行有限元计算分析的适用性。

4.1 算例验证

成层边坡示意图如图2所示。成层边坡均由不排水摩擦角φu= 0的黏土构成，土体容重γ= 20 kN/m3，有效内摩擦角φ′= 20°，上层边坡土体的竖直向黏聚力Su1=25 kPa，将下层边坡土体的竖直向黏聚力Su2与上层竖直向黏聚力Su1之比定义为强度比。应用不排水指标分析，取泊松比υ≈0.5，Eu= 400Su(与文献[29]中算例的弹性模量相等)。采用本文第2节中提出的相关联的修正Von-Mises准则，利用强度折减法进行有限元分析计算。边界条件设置为边坡上边界自由约束，左右边界水平约束，底部完全约束。

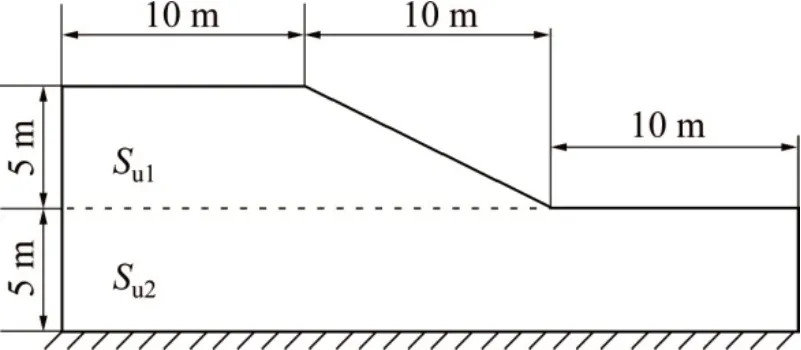
图2 成层边坡示意图Fig.2 Diagram of layered slope

GRIFFITHS 等[29]在计算时没有考虑土体强度各向异性，因此，这里取各向异性比k= 1 进行分析。经ABAQUS有限元软件计算后，结合文献[29]中的计算结果，得到边坡安全系数与强度比Su2/Su1的关系如图3所示。由图3可以看出：本文拟合结果与文献[29]中的计算结果具有相同的变化趋势，本文采用的是修正Von-Mises 准则，因此，本文结果较采用Mohr-Coulomb 屈服准则计算所得边坡安全系数大3%～7%。

图3 边坡安全系数与强度比(Su2/Su1)的关系Fig.3 Relationship between safety factor and strength ratio(Su2/Su1)

由图3还可以看出：边坡安全系数与强度比曲线存在1个明显的转折点，即强度比Su2/Su1约为1.5的位置。根据Su2/Su1的不同，提取ABAQUS 分析计算后3种典型的边坡失稳破坏模式，如图4所示。

分析图3和图4可知：当Su2/Su1＜1.5时，边坡失稳破坏的滑动面呈现典型的坡底圆形式，在这一阶段，随着强度比Su2/Su1逐渐增大，边坡安全系数基本呈现出线性增长模式；当Su2/Su1＞1.5 时，边坡失稳破坏的滑动面呈现典型的坡脚圆形式，此时，由于边坡上、下层土体的抗剪强度差异较大，当上层土体因强度折减而发生失稳破坏时，下层土仍具有较大的抗剪强度，还未产生较大的塑性应变，因此，这一阶段所对应的安全系数几乎保持不变；当Su2/Su1≈1.5，有限元计算不收敛时，2种失稳破坏形式同时体现在这个边坡上(见图4(b))。

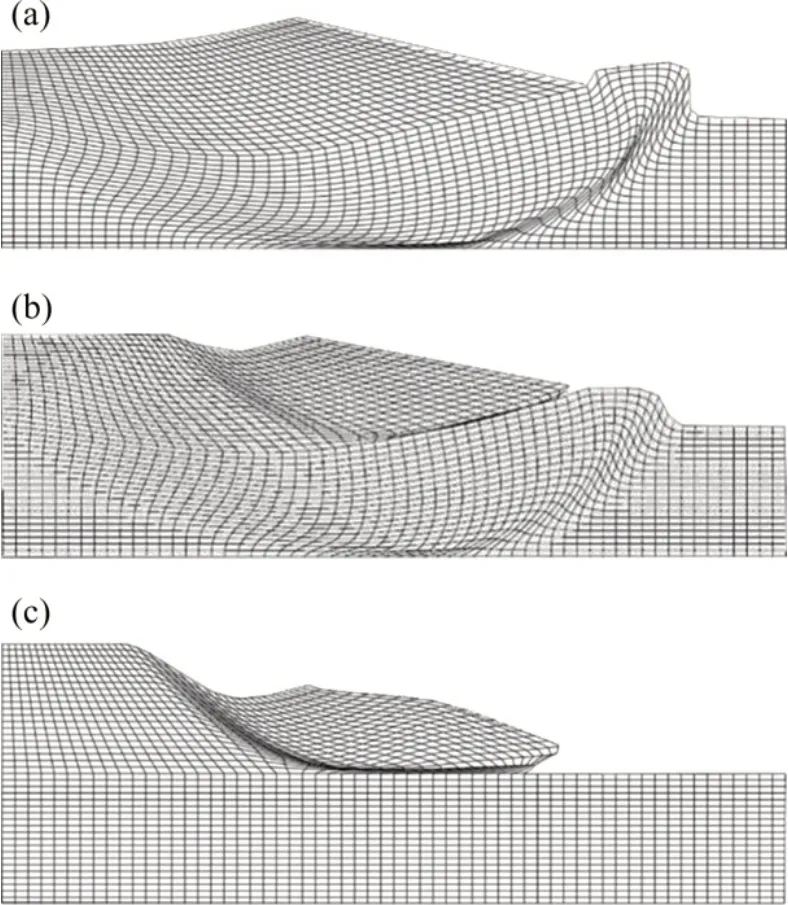
图4 不同强度比对应的边坡破坏形式Fig.4 Different failure types of slope corresponding to different Su2/Su1

同时，根据图4中的边坡破坏形式可以发现：随着Su2/Su1不断增大，边坡的失稳破坏形式逐步由坡底圆向坡脚圆发展，且当Su2/Su1约为1.5 时，边坡显示出2 种破坏形式都有所体现的叠合状态，这与文献[29]中的有限元分析结果一致。不同文献中成层边坡稳定性分析结果与本文计算结果对比如表1所示。由于不同文献中算例所采用土体参数均不一致，因此，没有选择对土体参数较为敏感的安全系数作为比较对象，仅从破坏形式方面与本文计算结果进行对比。由表1可以看出本文计算结果与文献[16，30-34]中的计算结果一致。

综上可知，本文的计算结果较为合理。下面针对以上3种典型的成层边坡破坏模式探究土体强度各向异性对安全系数的影响。

4.2 土体强度各向异性的影响程度

成层边坡算例的安全系数随各向异性比和强度比的变化如表2所示。由表2可知：不同强度比下边坡安全系数随各向异性比k的变化呈现相同的趋势。值得注意的是，当取各向异性比k= 0.8 时，安全系数反而较各向同性边坡(k= 1.0)的有所提升。这是因为，当利用本文式(12)进行分析计算时，不排水抗剪强度最大值和最小值并不在α= 0°和α= 90°方向上，而是出现在α=ϕ′/2 - 45°和α=ϕ′/2 + 45°方向上。因此，当各向异性比接近于1.0 时，若根据峰值抗剪强度确定成层边坡安全系数，则可能出现考虑强度各向异性后，边坡安全系数反而提高的现象。

为了直观地分析各向异性比对安全系数的影响，以各向同性成层边坡计算得到的安全系数为基准，得到边坡安全系数变化幅度T与各向异性比k的关系，如图5所示。

结合表2和图5可知：整体而言，当各向异性比较小(k≤0.8)时，无论Su2/Su1如何取值，随着各向异性比不断增大，边坡安全系数将逐渐增大，且当土体呈现较强的各向异性时(k= 0.4)，在3 种强度比下，有限元计算所得安全系数比各向同性边坡安全系数最大可减少50.77%；但对于不同强度比的成层边坡，其影响程度却呈现出一定的差异性。随着各向异性比增大，当Su2/Su1=1.0 即对应滑动面呈现典型的坡底圆形式时，安全系数首先迅速增大，之后增大趋势逐渐平缓；当Su2/Su1=2.0 即边坡最危险滑动面为坡脚圆时，安全系数呈现出先平缓增大后迅猛增大的趋势；而当Su2/Su1=1.5时，安全系数近似呈线性增大。这是因为：当各向异性比较小时，Su2/Su1=1.5 的最危险滑动面更倾向于坡底圆形式；随着各向异性比增大，其最危险滑动面向坡脚圆形式发展，直至k= 1.0 时对应的成层边坡失稳破坏呈现出2种滑动面形式都有所体现的叠合态。

实际工程中的边坡土体通常都存在不同程度的强度各向异性，但目前利用传统边坡稳定分析方法或有限元法评价其稳定性时大多按各向同性边坡处理，尤其是对于成层边坡，若不考虑各向异性比的影响，则往往容易过高估计成层边坡的稳定性，各向异性程度越大，相对误差越大。

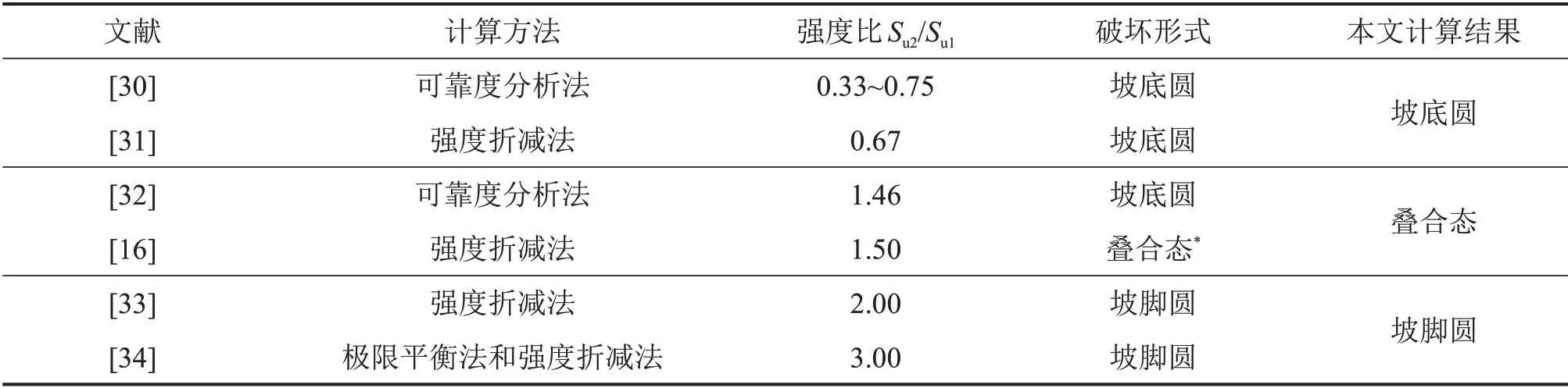
表1 成层边坡稳定分析计算结果对比Table1 Comparison of computing results of layered slope stability analysis

表2 安全系数随各向异性比和强度比的变化Table2 Variation of safety factor with the anisotropy ratio and strength ratio

图5 安全系数变化幅度T与各向异性比k的关系Fig.5 Relationship between safety factor change amplitude and anisotropy ratio

5 结论

1)提出能考虑土体有效内摩擦角的影响的各向异性不排水抗剪强度公式，同时得到能考虑土体强度各向异性的修正Von-Mises屈服准则，并结合有限元强度折减法编写了能计算各向异性成层边坡安全系数的ABAQUS 有限元模型；相较于传统边坡稳定分析方法，本文方法更为简便、准确，且当土体参数选用得当时，即使选用简单的弹塑性模型进行计算分析，同样可以得到较合理的计算结果。

2)当强度比Su2/Su1不同时，成层边坡的最危险滑动面呈现出3种不同的破坏模式，无论是何种破坏模式，若不考虑土体各向异性影响，则安全系数计算结果不准确；当土体呈现较强的各向异性时(k= 0.4)，有限元计算得到的安全系数甚至能比各向同性边坡的安全系数减少约50%。