考虑地下水影响的多层渣土边坡抗滑桩最大桩间距研究

2019-09-17曾江波张海宽2姚文敏2肖林超

长江科学院院报 2019年9期

曾江波，张海宽2，姚文敏2，肖林超

(1.深圳市勘察测绘院(集团)有限公司，广东深圳 518028； 2.中国地质大学(武汉) 工程学院，武汉 430074)

1 研究背景

渣土边坡是一种人类活动形成的渣土混合体边坡。随着我国经济发展对资源的需求，以及人类对于地下空间的探索，渣土边坡广泛分布于城镇、矿山等人类活动区周围。渣土边坡失稳会对人类的生命财产安全造成严重影响，如2015年12月20日在广东深圳某垃圾填埋场发生的大规模建筑垃圾滑坡事故，造成77人死亡，33栋房屋被毁[1]。抗滑桩支护是治理边坡运用最广泛的工程措施，而桩间距是设计抗滑桩的主要参数之一。

对于抗滑桩桩间距的确定，许多学者采用不同研究手段进行了研究。在试验研究和数值模拟研究方面，大多数学者对桩土相互作用方式和抗滑桩行为进行了研究，为抗滑桩桩间距的计算提供了一定依据。杨明等[2-3]基于物理模型试验和数值模拟探讨了抗滑桩宽度与桩间距对桩间土拱效应的影响；Song等[4]通过原位试验对抗滑桩进行研究，并通过SLOPILE程序计算稳定桩的行为，用于分析和设计抗滑桩；Li等[5]通过对三峡库区典型案例的研究提出了一种新的三阶段荷载传递模式，包括端承土拱、摩擦土拱和桩前滑体。在理论研究方面，大多数学者对于桩间距方法的研究是基于土拱效应进行的。周德培等[6]认为由于抗滑桩横向位移小于坡体的横向位移，桩后局部范围内的土体不断挤压桩体而产生不均匀的土压力，桩间的部分土体因受桩体约束作用不同而产生不同程度的剥落，从而产生了土拱效应；周德培等[6]和周应华等[7]在计算合理桩间距时考虑了土拱效应，并从抛物线形土拱出发，综合考虑了桩间静力平衡条件与土拱强度条件建立了合理桩间距计算方法；蒋良潍等[8]和贾海莉等[9]基于摩尔-库伦强度准则对桩间距计算方法进行了不同程度的改进；肖淑君等[10]在计算桩间距过程中认为桩间土拱轴线是合理拱轴线，将统一强度理论用于抗滑桩桩间距计算中，但仅适用于单层自然边坡的桩间距计算；张海宽等[11]提出了多层滑坡体模型中最大桩间距的计算方法，但这种计算方法是基于二维自然界滑坡模型提出的，其计算过程中也未考虑地下水的影响，不能完全适用于人工渣土边坡的研究。

在已有的抗滑桩桩间距研究中，大多数基于摩尔-库伦强度理论，研究对象为未考虑地下水的单层自然滑坡。但近年来位于人类活动区内的渣土边坡数量不断增加，对人类社会环境形成较大的威胁，所以对于人工渣土防护结构尤其是边坡桩间距的研究是十分必要的。鉴于此，本文构建了考虑地下水和不考虑地下水影响的2种典型多层渣土边坡模型，通过GEO-STUDIO搜索出多层渣土边坡中稳定性系数最小的滑动面。利用条分法计算得到2种边坡模型的剩余推力后，引入滑坡推力分布函数刻画设桩处边坡的应力分布特征。考虑土体的破坏规律，对桩间土拱模型进行了改进，基于统一强度理论的土拱强度条件和土拱平衡条件，即可求得每层滑体的最大桩间距，结合多层滑体间的相互作用就可以确定出2种典型多层渣土边坡模型的最大桩间距。最后通过深圳某渣土边坡计算实例验证了本文研究方法，对实际工程中多层渣土边坡最大桩间距的确定具有一定的借鉴意义。

2 渣土边坡抗滑桩最大桩间距的研究方法

2.1 统一强度理论

大多数对于抗滑桩桩间距的研究是基于摩尔-库伦强度理论进行的，这种强度理论算法虽然简单，但忽略了中间主应力对桩间距的影响，抗滑桩桩间距计算过程中的中间主应力往往是土体自重应力。鉴于此，本文引入考虑中间主应力的统一强度理论对桩间距进行计算。俞茂宏于20世纪60年代首次提出统一强度理论，在此基础上考虑到各种外凸与非外凸强度理论，于1994年将统一强度理论推广应用到岩土材料上[12]，其公式为

式中：σ1，σ2，σ3分别为最大、中间、最小主应力；a，σt分别为材料拉伸和压缩强度参数；b为反映中间主应力效应的统一强度参数，且当b=0,a≠1时式(1)为摩尔-库伦强度准则。俞茂宏等[13]引入中间主应力系数m，计算出σ2=mσ1+σ3/2，2ν≤m≤1(ν为材料泊松比)，为简化计算假定m=1[7]。c和φ分别为岩土体黏聚力、内摩擦角，将σt=2ccosφ/1+sinφ和a=1-sinφ/1+sinφ代入式(1)中有[13]

2.2 典型多层渣土边坡模型

为保证本文中最大桩间距的研究方法具有代表性，在罗平平等[14]研究的典型剖面土层分布模型基础上，提出不考虑地下水的多层渣土边坡模型(简称为模型1)和考虑地下水的多层渣土边坡模型(简称为模型2)，2种模型除了地下水外其他条件均相同。与不考虑地下水相比，在考虑地下水情况的桩间距计算中，除考虑土体中孔隙水压力变化，还考虑边坡土体参数如密度、摩擦角和黏聚力变化，这些参数改变也会使土体强度发生改变。

如图1所示，模型高50 m，底面总长度100 m，边坡有4层，从上到下依次为人工渣土、回填砖渣、粉质黏土、基岩(褐黄色粉质黏土)，边坡模型坡角为53°。各层土计算参数如表1所示。为分析地下水对桩间距的影响，本文在最大桩间距计算的每个过程中均对2种模型得到的结果进行对比。

图1 典型多层渣土边坡模型[14] Fig.1 Typical multilayer landfill slope models[14]

层号岩土类型密度/(g·cm-3)黏聚力/kPa内摩擦角/(°)天然饱和天然饱和天然饱和①人工渣土1.862.1218.011.819.211.6②回填砖渣1.992.2710.37.337.125.5③粉质黏土2.002.3255.237.515.39.7④基岩2.232.331.5×103 57

2.3 确定渣土边坡中的潜在滑动面

与天然边坡一般都存在软弱滑动面不同，渣土边坡中滑动面需要通过解析法或数值模拟方法确定。本文应用GEO-STUDIO数值模拟软件中的SLOPE/W分析模块对2种模型的滑动面进行搜索。对于模型1，选择无孔隙水压力情况，经过分析潜在滑动面结果如图2(a)所示，滑体稳定性系数为0.924；对于模型2，选择水压线选项对地下水位线进行绘制，输入模块参数过程中水位线以上参数为天然土体参数，水位线以下为土体饱和参数，搜索出潜在滑动面结果如图2(b)所示，滑体稳定性系数为0.713。对比2种模型的潜在滑动面，发现在考虑地下水情况下渣土边坡的滑体体积更大，但滑体的稳定性系数更小。

图3 典型多层渣土边坡剩余推力曲线Fig.3 Curves of residual thrust of typical multilayer landfill slope in the presence and in the absence of groundwater

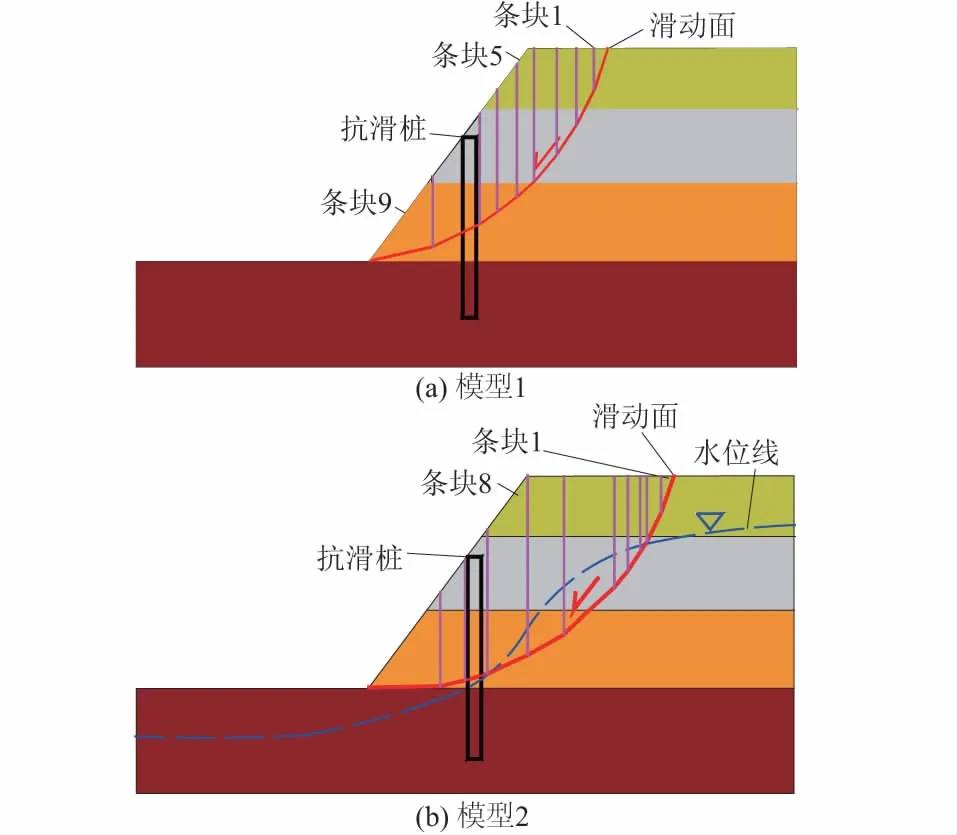
图2 典型多层渣土边坡模型的条分示意图Fig.2 Strips of typical multilayer landfill slopes

2.4 渣土边坡中剩余推力分析

确定边坡潜在滑动面位置后，使用条分法对2种情况下的滑体进行条分，在条分时注意滑动面及水位线的变化。将模型1滑体条分成9块，如图2(a)所示；将模型2的滑体条分成11块，如图2(b)所示。

条分完成后，运用剩余推力法[15]计算出各条分位置剩余推力。模型1、模型2的剩余推力如图3所示，横坐标原点为后缘在底面的投影点，横坐标表示在底面投影方法上滑体中某点距离滑体后缘的长度。考虑到滑坡推力大小及滑体厚度的影响，在如图2所示位置设桩，抗滑桩截面尺寸均为2.5 m×2 m。

2.5 多层渣土边坡抗滑桩最大桩间距的计算

图4 桩间土拱模型Fig.4 Model of soil arch between piles

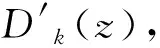
2.5.1 强度条件

已有的桩间距计算中，大多数是使用摩尔-库伦强度理论进行土拱强度判断的。根据肖淑君等[10]的研究，土拱的最危险点为拱脚点。由于合理拱轴线只受平行于拱轴线的压力作用，摩尔-库伦强度理论只考虑了σ1=Nkz,σ3=0，却忽略了土体自重应力σ2=σsz对桩间距的影响。所以本文使用统一强度理论判据在考虑土体自重的情况下对土拱强度进行研究，将主应力代入统一强度理论公式(式(2))中，有

(3)

式中：Nkz为作用在桩后三角形受压区的土拱压力；t为抗滑桩横截面长度；φk，ck分别为滑体k的摩擦角和黏聚力；βk为拱脚点处拱轴线与相邻桩中点连线的夹角；σkz为滑体k中最大应力深度处土体自重应力；Eb=b/1+b，为统一强度参数。肖淑君等[10]研究发现当滑坡推力为矩形分布时，Eb=0.23；滑坡推力为三角形分布时，Eb=0.375；当滑坡推力为梯形分布或抛物线型分布时，0.23

2.5.2 平衡条件

设置抗滑桩后，为防止桩间土体滑出，需要保证桩土之间可提供的最大静摩擦力大于桩间的滑坡推力。根据平衡条件有

(4)

在极限平衡状态下，研究最大桩间距时需要保证抗滑桩周围土体的受压三角形区发挥作用，根据图4(b)有

Nkzsinβk=Nkzcosβktanφk+ckt。

(5)

联立式(3)、式(4)、式(5)解出每层滑体的最大桩间距lk，即

式中：d为抗滑桩横截面宽度；ωk，μk为滑体k中与ck，φk，βk有关的函数，计算公式如式(7)所示。

(7)

联立式(3)、式(5)解出βk，如式(8)，其中Dk，Gk，Hk，Ak是计算过程中的参数。

(8)

将土体参数代入式(6)—式(8)，即可求得每层滑体对应的桩间距。

由于滑体间的相互接触、相互作用，在计算桩间距过程中需要考虑各滑体共同承受推力作用。设置抗滑桩后，稳定性强的滑体会对易滑滑体提供一定的抗滑力，这种抗滑力可以由相邻滑体对易滑滑体提供，此种抗滑力的存在会使每层滑体计算出的桩间距趋于相等，但由于各滑体性质的不同，最终的桩间距可能不会相等，所以存在如下关系：

(9)

以本文中的典型边坡模型为例，取安全系数FS=1.15，取滑体②中Eb=0.33、滑体③中Eb=0.375。计算出考虑地下水时最大桩间距l′=4.40 m，滑体②承受滑坡推力P2′=502.02 kN/m，滑体③承受推力P3′=1 743.02 kN/m。在不考虑地下水情况下最大桩间距l=7.36 m，滑体②承受滑坡推力P2=154 kN/m，滑体③承受推力P3=780 kN/m。2种模型结果对比显示考虑地下水模型的滑坡推力更大，但最终的桩间距更小。

3 实例分析

3.1 边坡概况

深圳市某渣土边坡场地原始地貌为丘陵，因场地大规模的人工堆填余泥渣土，现状地形已发生巨大改变，总体上场地处于山顶上，场地中间地形较为平缓，大致呈自东向西倾伏。在西侧、南侧及北侧边缘顺接原来冲沟的位置设置了人工边坡，地势相对较低，边坡总长约210 m，坡高约40 m，边坡后缘高程102 m，前缘高程60 m，高差约42 m，剖面图如图5。

图5 深圳某渣土边坡剖面图Fig.5 Profile of a landfill slope in Shenzhen

根据钻探揭露，场地内各土体物理参数如表2所示，岩性特征自上而下依次描述如下。

余泥渣土层(Qml)成分为人工填土(地层编号①)：灰褐、黄褐、红褐等色，以黏性土、砂土为主，含大量碎石、混凝土块、砖头等建筑垃圾及杂填土。

第四系中更新统残积层(Q2el)成分为粉质黏土(地层编号②)：褐黄、褐红等色，由下伏基岩风化残积而成，原岩结构尚可辨认，含10%左右的石英砂。

震旦系地层(Zh)石英片岩：灰白、褐黄色，主要成分为石英、长石等，变晶结构，片理构造。按其风化程度及钻探揭露情况可分为强风化层(地层编号③)、中风化层(地层编号④)。

表2 深圳某渣土边坡土层参数Table 2 Parameters of a landfill slope in Shenzhen

3.2 最大桩间距计算

使用GEO-STUDIO数值模拟软件分析深圳某渣土边坡剖面(如图5所示)，然后对该坡面进行条分，根据滑坡剩余推力大小及滑动面深度选择如图5中位置设桩，取安全系数为1.15，抗滑桩截面尺寸为1.8 m×2.2 m，所需承受推力P=713.24 kN/m。

由于人工渣土以黏性土、砂土为主且含有建筑垃圾及杂填土，根据戴自航[16]的研究取梯形推力分布形式进行计算，取Eb=0.30，计算出最大桩间距l=4.16 m。当取b=0，即Eb=0时，即基于摩尔-库伦强度准则的土拱强度条件和土拱平衡条件计算出的最大桩间距为3.71 m。最大桩间距是抗滑桩间距选取的上限值，根据现场原位试验和相关资料，实际设桩桩间距为4.0 m>3.71 m，如果采用摩尔-库伦理论对桩间距进行设计，虽然可以保证边坡稳定，但可能会造成材料的浪费。实例结果表明本文方法设计出的桩间距可以保证滑坡的稳定性，同时也证明基于统一强度理论计算桩间距的方法合理。