海堤龙口水力计算方法探讨

(浙江省水利水电勘测设计院，杭州 310002)

1 研究背景

浙江沿海地区在滩涂保护与利用开发中，海堤龙口段的地基大多数为深厚淤泥软土地基，受进排水要求限制，海堤龙口段抛填石料厚度一般较薄，其预压固结程度不如一般海堤段的预压固结程度，其抗冲刷能力相对较差。龙口宽度太窄则龙口度汛期涨落潮时水流相对较急，容易造成龙口严重冲刷，影响工程安全稳定性；龙口宽度太宽则造成堵口难度大，影响工程总体工期，且不易合龙。因此，选择合适的龙口宽度在深厚淤泥地基海堤工程中显得尤为重要。

吴继伟[1]采用水量平衡法编制了海堤龙口水力计算软件，但其未考虑龙口在堵口过程中底坎、口门宽度的动态变化过程，且对堵口过程中抛石底坎的透水性以及水闸的影响等要素未深入考虑，软件计算模型仍有待深入细化。

赵庚润等[2]利用流体有限元软件Fluent中的k-ε湍流模型对海堤龙口二维流动进行了数值模拟计算，认为落潮时龙口最大流速可达8.70 m/s，涨潮时龙口最大流速可达10.60 m/s；其中大流速区一般位于堤顶或背流侧的区域；甚至龙口附近会出现水跃或者卷浪型流态。

胡志根等[3]采用物理模型试验对大比降、非对称基床中的合龙进行研究，观测分析堵口合龙进占方式、龙口位置、龙口水流流态及其龙口水力参数之间的关系。

杨磊等[4]通过相关模型试验对宽戗堤龙口堵口范围内的水流特性进行试验研究，认为当宽戗堤堤顶宽度B与总水头H0的比值B/H0在311～517之间时，龙口内水面形态将逐渐由单降型流态渐变为双降型流态；但当B/H0>517时,龙口戗堤堤顶的宽度效应逐渐减弱。

工程实际海堤龙口计算中外海潮位等水力边界条件不断变化，导致龙口水力计算较复杂，一般需采用简化小程序计算(如文献[1])。基于此，本文依据水力学理论，结合MATLAB软件，采用黄朝煊等[5]研究中给出Runge-Kutta法对海堤龙口水力计算进行分析研究，以便工程应用推广。

2 龙口水力计算基本方程

根据文献[6]和文献[7]可知，由围区内进(出)水量平衡原理得龙口水力计算基本方程为

(1)

q外=q闸+q泄+q渗，

(2)

(3)

(4)

式中：q内为内陆流域来水平均流量(m3/s)；q外为受外海潮位影响流进(出)围区的流量(m3/s)；q闸为水闸过流流量(m3/s)；q泄为口门堰上溢流流量(m3/s)；q渗为计算时段内海堤龙口抛石体渗流平均流量(m3/s)；V[Z(t)]为t时刻围区内库容量(m3)；Z(t)为t时刻围区内水位(m)；h(t)为t时刻外海侧潮位(m)；F[Z(t)]为围区水位为Z(t)时的水面面积；mμ为龙口水力计算的流量系数；Bω为实际等效过流计算宽度；k为参数，堰流时k=1.5。

由于外海潮位、围区库容等边界条件为非线性性关系，因此，以上龙口水力计算方程为非线性常微分方程，目前还难以给出其解析解。

3 基于四阶Runge-Kutta法的龙口水力计算

根据以上方程式(1)—式(4)，代换后可得水力计算控制方程为

(5)

记

则式(5)可简化为

(6)

可采用经典的四阶Runge-Kutta法求解控制方程得

(7)

其中：

K1i=fti,Zti；

K4i=fti+Δt,Zti+ΔtK3i。

式中： Δt为计算时间段的步长；Zti为在ti=iΔt时刻的围区水位；K1i,K2i,K3i,K4i为i时段的积分参数，由Z(ti)，ti等计算确定。

根据以上数值计算法，可由外海侧起调潮位、围区侧起调水位Zt0等边界条件计算求解出围区水位随时间的过程线Z(t)，其中Runge-Kutta法的求解流程如图1所示，可利用MATLAB[8-9]软件数值编程计算实现，其中计算时间步长Δt一般可取0.1～0.5 h。

图1 Runge-Kutta法求解过程示意图Fig.1 Sketch of the solution process of Runge-Kuttamethod

其中深厚淤泥地基上的海堤龙口典型断面如图2所示。

图2 深厚淤泥地基上的海堤龙口典型断面示意图Fig.2 Schematic diagram of the closure gap section of sea dyke on deep silt foundation

4 龙口最大水位差的解析分析

由于外海潮位的近似周期性变化特性，假设外海侧潮位过程线为

(8)

其中，

式中：h为潮位；T0为潮位半周期，即潮位周期为2T0；H为最大潮差;χ为平均潮位。

龙口、水闸等总过流能力的计算公式为

(9)

在忽略内陆来水情况下，依据式(1)流量平衡方程得：

(10)

(11)

其中围区侧起调水位取为Z0，参数Z0为海堤龙口底槛高程；值得说明的是，在落潮时需对式(11)取绝对值。

将式(11)代入式(10)可得

(12)

按照工程计算经验，在最不利水力条件即围区侧水位与外海侧潮位之间最大水位差情况(如图3所示)[11]一般出现在高潮位之后，即满足dH0/dt=0时，对式(11)两边求导，变化可得

(13)

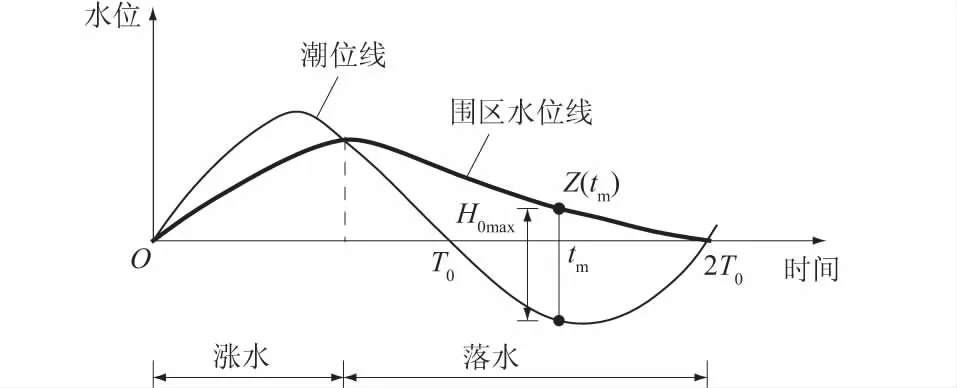
图3 潮位与围区内水位关系曲线示意图Fig.3 Relation between tide level and water level in the closure area

在龙口水力计算中，主要水力参数是围区水位与外海潮位间水位差最大值H0max，其中根据浙江省水利水电勘测设计院龙口水力计算经验，最大水位差出现的时间一般为tm=t0+(1.0～1.5)T0，即低潮位之前(0～0.5)T0。记龙口内外两侧水位差最大时刻为tm，此时最大水位差为H0max，相应围区水位为Z(tm)。

将式(13)代入式(12)，则得

(14)

由于式(14)具有2个待求变量tm和Ztm，还需要1个方程才能求解，根据水量平衡建立方程，即

(15)

式中参数K为围区库容修正系数，一般取值为1.0～1.2。

由式(14)和式(15)，通过数学变换，可得以下非线性代数方程组，即

根据方程组(16)，求解非线性方程组可解出待求参数tm和Z(tm)。

(17)

依据浙江省水利水电勘测设计院龙口水力计算经验，一般μ=1.0～1.50，借助MATLAB软件计算求解出μ和tm，并根据式(8)和式(11)给出最大水位差H0max计算式。

设围区侧的库容曲线满足二次抛物线，即

V[Zt]=a2Z2t+a1Zt+a0。(18)

对式(18)求导可知

F[Zt]=2a2Zt+a1。

(19)

式中常参数a0,a1,a2根据实测库容关系曲线拟合得出，将V[Z(t)]以及F[Z(t)]代入以上非线性代数方程(17)，得到最大水位差时龙口围区侧水位与龙口宽龙口底坎高程之间的关系函数。

外海潮位与围区水位之间的最大水位差为

(20)

进而依据《滩涂治理工程规范》[6]和《海堤工程设计规范》[7]可知最大流速为

(21)

根据式(17)、式(20)及式(21)，可对龙口水力特性进行计算分析，并能绘制涨潮、落潮时的围区潮位最大水位差与龙口宽度关系曲线，进而能给出龙口段涨潮、落潮时的最大水流流速等水力特性，为工程实际中深厚淤泥地基海堤龙口抗冲刷设计提供计算依据。

5 算例分析

5.1 项目概况

某围垦工程围垦面积2 296.6 hm2，工程主要由海堤、水闸、施工道路等组成。根据防护对象的规模和重要性，确定工程防潮(洪)标准为50 a一遇。该工程海堤级别为3级，水闸级别同为3级，施工道路、河道等次要建筑物为4级，围堰等临时建筑物为5级。海堤地基土层主要为Ⅲ0层淤泥、Ⅲ1层淤泥质粉质黏土、ⅢSis粉砂、粉土混淤泥、Ⅲ2层淤泥、Ⅳ1淤泥质粉质黏土、Ⅳ2层粉质黏土、黏土组成。

其中龙口布置原则：①龙口位置宜考虑围区涂面较低部位，以利于围区潮流进出；②龙口位置应离水闸有一定距离，以免影响水闸施工和水闸泄流影响堵口；③龙口型式采用“宽高式龙口”龙口。根据龙口水力条件，为减小龙口流速防止冲刷和简化保护措施，目前浙江省大中型围垦工程和堵港工程的度汛龙口型式均采用“宽高式龙口”，即龙口宽度尽可能宽一些，底槛高程适当抬高。

5.2 龙口水力计算

该工程围堤龙口度汛设计潮型，以非汛期5 a一遇设计高潮位3.94 m为控制水位，将典型潮位过程作适当修正后采用；围堤度汛期设计潮位见表1。

表1 龙口度汛期设计潮位过程线Table 1 Process of design tide level at closure gap in flood season

其中通过MATLAB软件对外海设计潮位进行数值拟合分析得

h(t)=0.76+2.67sin0.507t+1.407 。 (22)

其中潮位过程线与拟合函数关系如图4所示。

图4 龙口度汛期设计潮位过程线及数值拟合Fig.4 Process and numerical fitting of design tide level at closure gap in flood season

该工程围堤内侧库容与围区水位关系通过实测地形曲线量算，见表2。

表2 围区库容-水位关系

通过MATLAB软件数值拟合，给出库容-水位关系曲线(见图5)，拟合函数为

V[Z(t)]=39.2Z2(t)+460Z(t)+453 。

(23)

图5 围区库容-水位关系曲线及数值拟合Fig.5 Measured and fitted relation between storage capacity of closure area and water level

根据本文方法，对该围垦工程龙口水力条件进行计算研究，其中涨潮、落潮时龙口最大流速Vmax与龙口底高程Z0、龙口宽度B之间关系曲线族见图6。

图6 龙口最大流速Vmax与龙口底高程、 龙口宽度B之间关系曲线族Fig.6 Set of curves of maximum flow velocity Vmax at closure gap versus bottom height and width of closure gap

通过以上数值计算分析可知：当底槛高程在0.0以上时，龙口处涨落潮流速随龙口宽度增大而减小，且流速变化较明显；当底槛高程取为1.0 m以上时，龙口处涨落潮流速随龙口宽度变化相对较小。

根据龙口布置及控制涨落潮流速等一般要求，同时结合本工程涂面高程实际情况，以最大控制流速不大于3 m/s，通过以上数值计算，最终设计选定龙口底槛高程0.5 m，龙口设计宽为300 m。

6 结论与建议

针对深厚淤泥软土滩涂的海堤龙口抗水流冲刷能力较差的问题，本文对海堤龙口水力学特性进行了研究分析，主要结论如下：

(1) 依据水力学理论及水量平衡原理建立了海堤龙口水力计算基本方程，该方程为非线性常微分方程，一般情况下难以给出精确解析解，可依据数值分析理论利用经典四阶Runge-Kutta法求解，结合MATLAB计算软件数值编程给出数值解，其中计算时间步长Δt一般可取0.1～0.5 h。

(2) 利用正弦函数拟合外海潮位周期变化特性，利用二次函数拟合围区库容-水位关系曲线，结合相关数值等效分析法及海堤龙口计算经验，给出了海堤龙口最大水位差与龙口宽度之间的近似解析计算方法，为工程实际应用提供方便。

(3)最后通过工程案例，利用MATLAB软件计算对比分析，表明该案例中底槛高程在0.0以上时，龙口处涨落潮流速随龙口宽度增大而减小，且流速变化较明显；当底槛高程取为1.0 m以上时，龙口处涨落潮流速随龙口宽度变化相对较小，与工程实际经验一致。

值得说明的是，由于涨落潮时口门上水流流态较复杂，涉及高淹没出流情况，因此本文简化计算方法难免存在一定不足，笔者将进行后续深入研究。