限制平均生存时间在区间删失数据中的应用*

黄兴辉 吕晶晶 杨紫荆 侯雅文 陈 征△

【提 要】 目的 针对区间删失生存数据的分析研究，提出限制平均生存时间(restricted mean survival time，RMST)的估计和两组比较检验。方法 利用修正EM算法进行迭代并得到生存率估计值，并基于此估计值构建RMST检验统计量求得P值，通过Monte-Carlo模拟验证其统计性能。结果 本文提出的区间删失生存数据中RMST检验法的I类错误在0.05附近波动，且其检验效能与现有常用方法Sun模型相当。结论 针对区间删失生存数据的组间比较，本文提出RMST检验法不仅准确估计各组生存率，且通过计算RMST能够直观解释组间差异大小并由此作出统计推断，具有较好的统计性能，为临床研究者和病人提供决策依据。

在医学临床研究中，通常需要对事件发生时间进行观测，并进一步分析评价。当只知道事件发生在某一特定区间内，而不知道其确切的时间点时，将这类数据称为区间删失数据[1-3]，表示为T∈(L,R)，其中T表示个体的生存时间，L表示删失区间的下界，R表示上界。目前对于区间删失数据，现有一类广义log-rank检验较为常用，例如Sun模型[4-5]，该方法基于单个区间内实际死亡数与理论死亡数的差值构造统计量，但是该类方法难以直观解释差异大小且可能会出现不收敛的问题；有研究[6-8]表明，限制平均生存时间(restricted mean survival time，RMST)表示从研究起始时间到一个特定时间点τ上的平均生存时间，即对应于时间点τ前的生存曲线下面积大小，并且针对该指标差值或者比值进行检验称为RMST检验，能够简单描述生存状态下平均生存时间的差异大小，在进行组间比较时应用广泛[9-10]，特别是当风险率成比例假定不成立或者感兴趣的事件数较少时，该指标能够更加有效反映预后效果[11-12]。本文利用修正EM算法进行区间删失数据的生存率估计，由此构造RMST检验统计量，对应提出区间删失生存数据下的RMST检验法，通过模拟探索其稳健性和适用性并进行实例分析。

方法介绍

1.区间删失生存数据中的RMST估计

(1)

对似然函数取对数，并对pj求偏导数得

i=1,…,n;l=j=1,…,m

(2)

如图1所示，对某戒毒中心的940名静脉注射毒品患者经过戒毒治疗后的HIV感染数据进行分析[14]，假设截止时间点为τ(最后一个观察者的生存时间或者是最后一个事件者的死亡时间或者是某个给定的时间点，本研究取两组中最大区间端点的较小值)，则限制性生存时间为X=min(T,τ)，由此可得X的期望，即限制性平均生存时间可以表示如下：

(3)

S(t)为生存函数，μ为区间[0,τ]上生存函数的积分，即对应于生存函数S(t)曲线下面积。

进一步计算E(X2)，即

E(X2)=E(T2|T≤τ)Pr(T≤τ)+τ2Pr(T>τ)

(4)

由于Pr(T≤τ)=1-S(τ)，则

(5)

故X的方差可以估计如下：

Var(X)=RSDST2=E(X2)-[E(X)]2

(6)

其中，RSDST为限制性标准差。

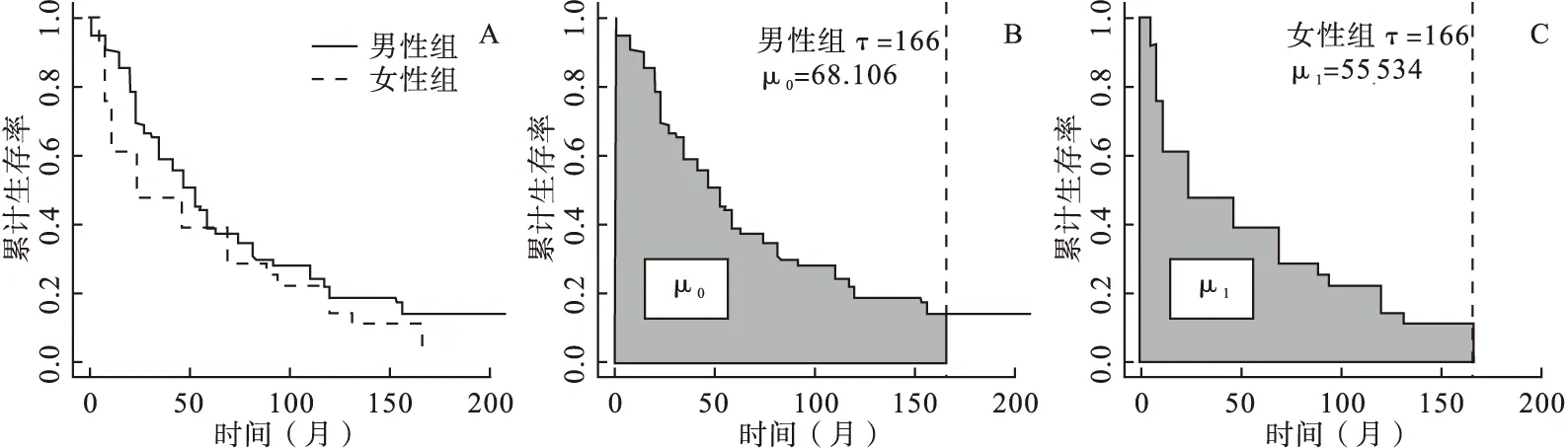
图1 经戒毒治疗后的HIV感染

图1A为通过修正EM算法分别估计两组的生存曲线图，图1B、图1C阴影部分面积分别为两组限制性平均生存时间的估计值，其中限制性平均生存时间及其方差的估计值如下：

(7)

(8)

2.区间删失生存数据中的RMST检验法

比较两组间生存率的差异，原假设是在任意时刻点t上，两组对应的生存率相等，即H0:S1(t)=S2(t)，备择假设H1:S1(t)≠S2(t)。根据限制性平均生存时间构造统计量，即在时间点τ上计算两组限制性平均生存时间的差值Δ：

(9)

S0(t)，S1(t)分别为第一组、第二组的生存函数；μ0，μ1分别为第一组、第二组的限制性平均生存时间。

根据修正EM算法可得：

根据delta法进一步估计其方差：

(10)

在原假设、大样本下该检验统计量服从t分布或正态分布[10]。

模拟研究

本文采用Monte-Carlo模拟来探索区间删失生存数据中RMST检验法的检验效能和I类错误[5]，评价其稳健性和适用性。生存时间T：由参数为(α+βzi)的指数分布产生，zi是组别指示变量(zi=0表示对照组，1为试验组)，即对照组、试验组的生存时间T分别服从风险率为α、α+β的指数分布，且β表示试验组与对照组风险率的差值。删失区间产生：首先产生分别服从均匀分布(1,θ1)和(1,θ2)的相互独立U1,U2，其中θ1,θ2是大于1的常数；然后定义U为U1四舍五入后的值，定义V为max(U1+U2,U+1)并取四舍五入后的值，由此产生删失区间(U,V]；模拟通过θ1,θ2的不同取值控制左删失(生存时间T小于删失区间下限)、区间删失(生存时间T位于删失区间之间)及右删失(生存时间T大于删失区间上限)的比例。本研究设置α=0.2，n1=n2=30,100,200，循环次数设为1000次。

表1展示了不同样本量、删失百分比和β取值时两种检验法的I类错误和检验效能，当α=0.2，β=-0.1，-0.05，0，0.05，0.1时，即固定第一组生存时间T服从风险率为0.2的指数分布，第二组生存时间T分别服从风险率分别为0.1，0.15，0.2，0.25，0.3的指数分布。表1第一列分别对应模拟数据中左删失、区间删失、右删失所占比例，本文考虑了(1/3,1/3,1/3)和(1/4,1/2,1/4)两种删失率组合。从表1可见，当β=0时为I类错误：在不同删失比例、不同样本量组合下，两种方法的I类错误都在0.05附近波动，RMST检验法在删失比例为(1/3,1/3,1/3)且样本量为(30,30)时I类错误偏小。当β≠0时为检验效能：样本量为(30,30)时，两种方法的检验效能交替较高；样本量为(100,100)和(200,200)时，当β=-0.1和0.1，Sun模型较高，当β=-0.05和0.05，RMST检验法较高。

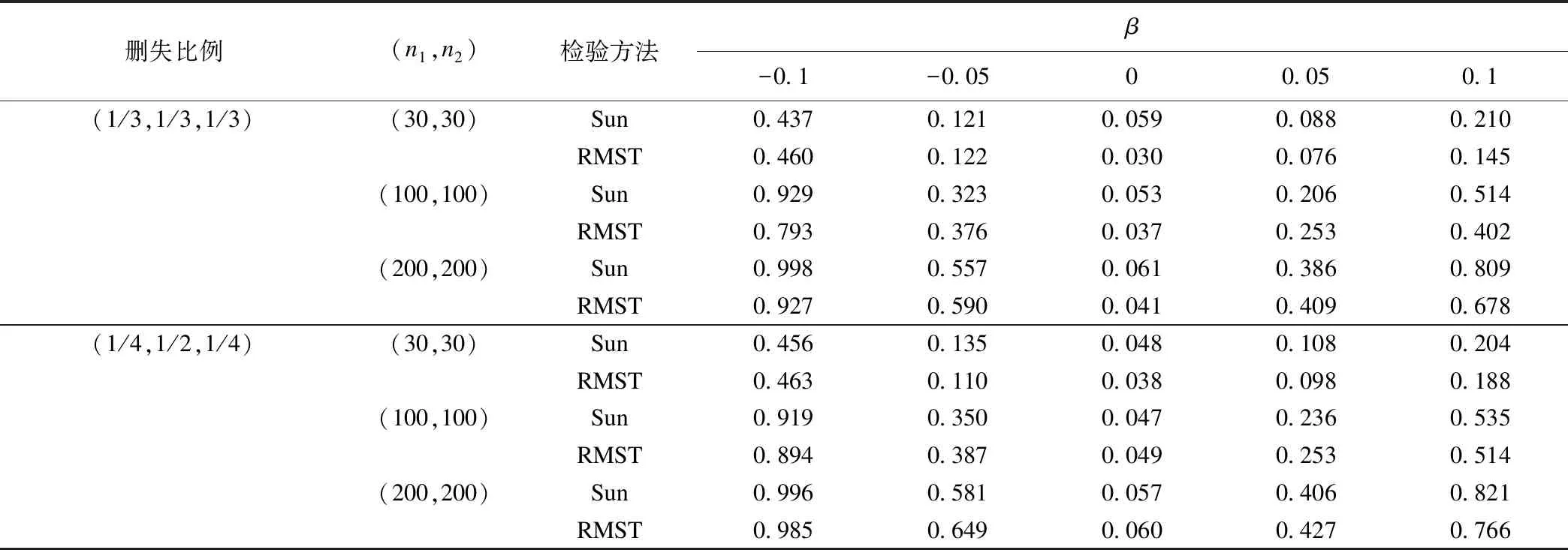
表1 I类错误和检验效能

*：α=0.2。

总体来说，本文提出的区间删失生存数据中RMST检验法与常用的Sun模型均能较好控制I类错误，并且除了小样本外具有较高的检验效能，具有较好的统计性能。

实例分析

对某戒毒中心的940名静脉注射毒品患者经戒毒治疗后的HIV感染数据进行分析[14]，该研究起始时间是戒毒治疗的开始，终点事件定义为发生HIV感染，研究中心以月为单位定期检查血清情况，由此确定在每个观察区间内是否发生终点事件。因发生HIV感染的确切时间并不能被直接观察到，即可将这些患者感染HIV看作区间删失型数据；若患者在观察期内未发生终点事件，则为右删失数据。根据性别进行分组，男性组有759例患者，女性组有181例患者。

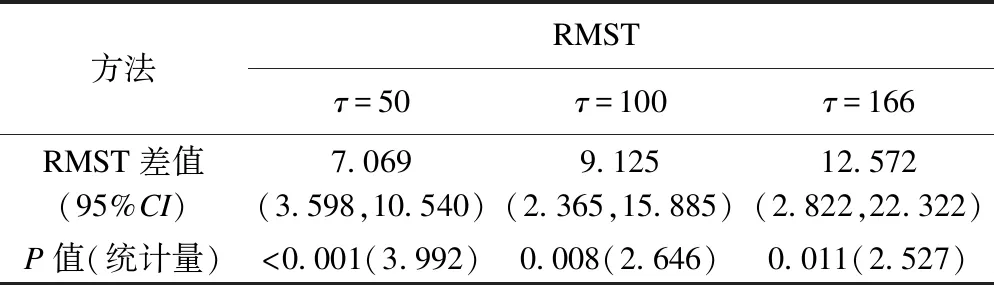
表2 RMST检验法的实例分析结果

*：Sunχ2=3.448,P=0.063。

由图1和表2可见：当τ取两组最大区间端点的较小值(即τ=166)时，在男性中限制性平均生存时间μ0=68.106个月(图1B中生存曲线下面积值)，在女性中限制性平均生存时间是μ1=55.534个月(图1C中生存曲线下面积值)，故男性与女性的限制性平均生存时间差值为12.572个月，且其对应的95%可信区间为(2.822,22.322)，RMST检验统计量z=2.527，P=0.011，提示在戒毒治疗开始至第166个月，男性组、女性组的平均HIV感染时间有统计学差异，且男性较女性长12.572个月；假如研究者关心的时间点是截止到第50个月(即τ=50)时，男性组、女性组的平均感染时间分别为36.928、 29.859个月，其差值及95%可信区间为7.069(3.598,10.540)，z=3.992，P<0.001；同理，假如研究者关心的时间点是截止到第100个月(即τ=100)时，男性组和女性组的平均感染时间分别为54.721、45.596个月，其差值及95%可信区间为9.125(2.365,15.885)，z=2.646，P=0.008。对于Sun模型，χ2=3.448，P=0.063，该检验法只能给出两组差异的整体性检验结果，即提示两组HIV感染时间没有统计学差异。

讨 论

本研究结合修正EM算法，在区间删失生存数据中进行RMST检验法的发展与应用。本文提出的RMST检验法既保证了生存率的准确估计，又对区间删失生存数据中组间差异进行直观阐述和比较；不管风险率是否成比例，该检验法均通过两组生存曲线下面积差值构建统计量，能够直观反映在τ时刻前平均生存时间的差异大小，并做假设检验，在事件数较少时依然适用，为临床研究者和病人提供平衡风险-成本-效益(risk-cost-benefit)并作出决策的依据。由上述实例分析结果可知，τ的选取对结果的影响较大。截止时间点τ需要在实验设计阶段就明确定义，并且其不同取值对应不同的限制性平均生存时间，从而导致检验结果有所不同。本研究实现了在区间删失生存数据中RMST检验的拓展，并通过模拟验证其能够较好地控制I类错误同时具有检验效能，但尚未与其他现存检验方法进行全面比较。此外，本研究只考虑了两组的情况，涉及多组的组间比较有待进一步推导和完善。