基于动态门限的幅度调制空间相干光通信系统

孙 鑫， 李 林

(1. 长安大学 现代工程训练中心， 陕西 西安 710064;2. 中国科学院 长春光学精密机械与物理研究所， 吉林 长春 130033; 3. 中国科学院大学， 北京 100049)

1 引 言

近年来，随着科技的发展，激光技术有了广泛的应用[1-7]。在这些应用中，无线激光通信技术由于其具有高传输速率、高安全性、无需频带许可等优点，获得了广泛的关注[8-11]。然而，由于大气湍流所引起的衰落的影响，其通信链路的性能会大大降低[12-15]。在这一过程中接收端接收到的信号的幅值和相位都会产生很大畸变，从而使得传统光通信系统的误码率性能急剧恶化。

为了在较低的复杂度下获得更好的误码率性能，一些研究将重点放在了自适应动态门限上。之前的部分研究倾向于假设接收机已知大气衰落的瞬时值，并使用信道状态信息(CSI)对信号进行检测[16-19]。然而在现实中，接收机很难获得瞬时信道状态信息(CSI)。在参考文献[20]中，作者们利用冗余的帧头导航序列来减轻大气湍流的干扰，进而提高系统性能。但是这一方法由于需要先对整个序列进行存储，然后再进行处理，因而会引入延迟。此外，该方法仍需要信道概率密度函数的辅助来实现。

为了解决以上问题，本文首先提出了一种基于动态门限的幅度调制空间相干光通信(IM/CD)方案。该方案无需瞬时信道状态信息和大气湍流模型的概率密度函数就可以实现对信号的高精度检测，与此同时该方案亦能通过提高本振激光器的功率来获取更好的误码率性能。此外，为了进一步研究其性能，本文推导了该方案平均误码率的表达式。实验结果表明该方案可以在较低的复杂度下获得较好的误码率性能。

2 系统结构

系统结构如图1所示。系统发射端利用一个马赫-曾德尔调制器(MZM)来调制激光光束。调制器的同向(I路)和正交(Q路)支路被用来发送两个不同的特殊信息序列。其中，这两个序列通过一定的编码规则来确保在每一个码元周期内至少有一个支路发送“1”。

如图2所示，为了获取这两个特殊序列，我们首先将一个长度为3的二进制码组转换为一个长度为2的三进制码组。这一映射可以表示为：

{0,1}3→{0,1,2}2,

(1)

然后我们再将得到的三进制码组中的每一个元素转换为一个长度为2且不包含“00”状态的二进制序列。其具体的映射规则为：三进制码组中所包含的3种元素(0,1,2)分别对应{01,10,11}3个二进制序列。最后将得到的二进制序列通过串行-并行转换后发送到调制器的两条支路，并将经调制后的光信号通过镜头发射出去。这一过程可以表示为：

{0,1,2}2→{0,1}4.

(2)

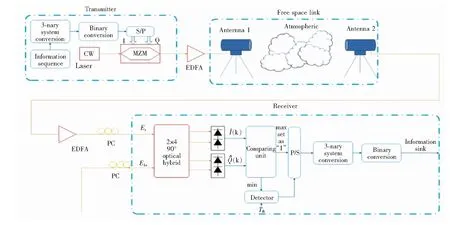
图1 系统结构模型。

上文所述的映射过程可以保证接收端在每一个码元周期内都能够获得一个较为准确的大气湍流衰减的参考。这是由于在每一个码元周期内，发送端至少有一条支路发送信号“1”。而每一个被发送的信号“1”都会受到大气湍流的影响，因而其可以被视为大气湍流衰减的参考。

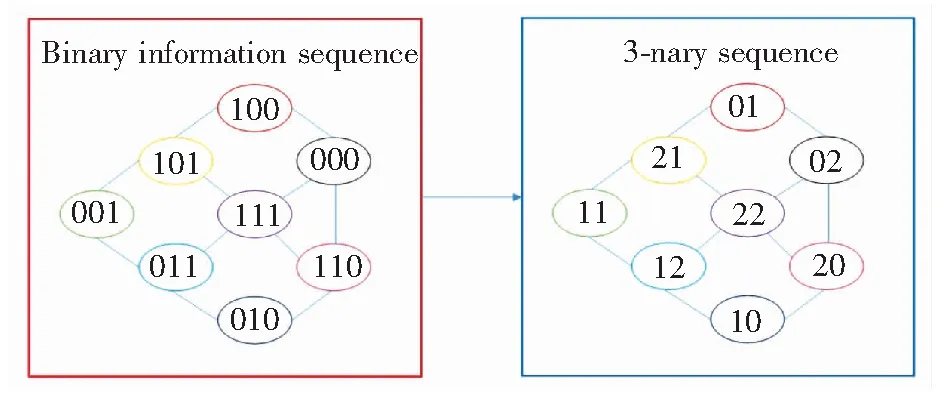
图2 二进制码组到三进制码组映射图

Fig.2 Diagram of mapping binary code groups to 3-nary code groups

在接收端，如图1所示，首先利用一个掺铒光纤放大器(EDFA)对接收信号进行放大，然后将经放大后的信号Es送入零差相干接收机进行探测。在这一过程中本振光ELO和经放大后的接收信号光Es的偏振态由偏振控制器来保证。接收信号光Es和本振光ELO在2×4 90°光混频器中进行混频，其输出的光信号被两个平衡探测器(BD)转化为电信号供后续模块处理。在每个码元周期内，后续处理模块首先将平衡探测器输出电信号中信号幅值较大的支路设为“1”，然后将该支路信号幅值大小的一半设为另一条支路的判决门限，并对另一条支路进行判决。判决后的信号经过并行-串行转换后被送入三进制转换单元。该单元将4位二进制序列转换为长度为2的三进制码组，并将得到的三进制码组送入二进制转换单元。最终二进制转换单元将三进制码组映射回长度为3的二进制码组以获得信宿。

在发射端，发射信号可以被表示为：

S(t)=EI[A(t)cos(2πfct)+B(t)sin(2πfct)],

(3)

其中EI代表发送信号的幅值，A(t),B(t)∈{0,1}为两条支路中的数据，fc代表发送载波频率。两条支路的信号幅值经大气信道传播后会发生畸变，这一过程可以视为一个乘性的随机过程I(t)。这里我们假设两条支路在同一时刻所受到的大气衰落影响是相同的。这是由于两条支路波长相同且光路重叠[21]。

所以在接收端经过平衡探测器后的输出信号可以表示为：

yI(t)=REIELOI(t)·

[A(t)cos(φn)+B(t)sin(φn)]+n1(t),

yQ(t)=REIELOI(t)·

[B(t)cos(φn)+A(t)sin(φn)]+n2(t), (4)

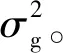
3 系统平均误码率分析

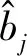
3.1 当发射端发送三进制符号bj时，接收端判决结果为三进制符号时的条件概率

由上文可知，系统的判决门限随发射端发送的三进制符号的变化而变化。当发射端发送“0”时，系统的判决门限为：

Tth(0)=

(5)

当发射端发送“1”时，系统的判决门限为：

Tth(1)=

(6)

当发射端发送“2”时，系统的判决门限为：

(7)

(8)

其中EI[•]和Eφn[•]代表对I和φn求期望。

3.2 系统平均误码率

(9)

(10)

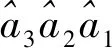
其中⊕代表异或运算。因此系统的平均误码率可以表示为

P(e)=

(12)

在公式(12)中，由于a3a2a1中的元素相互独立，所以我们可知P(a3a2a1)=1/23。

将公式(10)代入公式(12)，可得到

(13)

4 实验仿真结果

我们对本文所提出的系统的误码率进行了仿真。为了叙述方便，我们用Pi表示系统发射功率、Pl表示接收端本振激光器功率。同时我们认为大气湍流所引入的随机衰落过程服从对数正态分布。此外，我们假设信号由于在大气中长距离传输所产生的衰减是固定的，且可以被接收端的EDFA补偿。

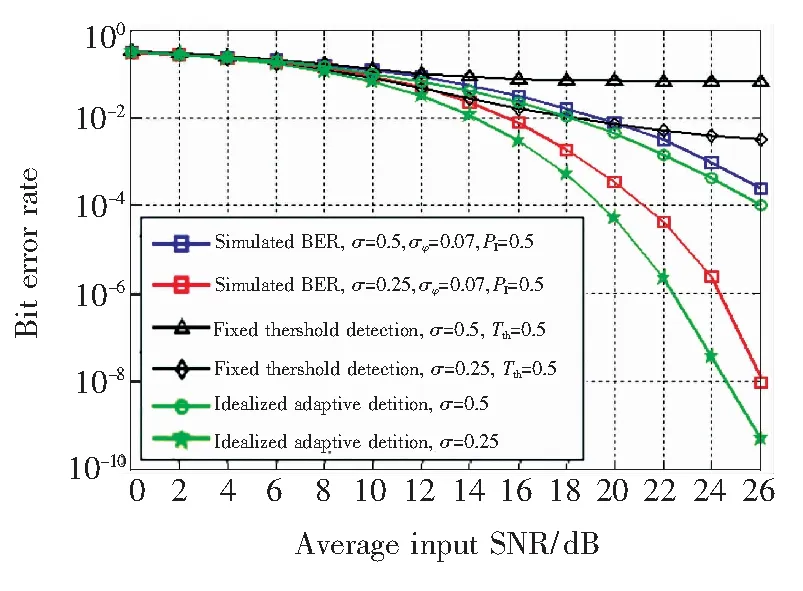
图3 各系统在不同的大气湍流条件下的仿真误码率

Fig.3 Simulated BERs of different systems over different turbulence channels

图3为理想自适应判决门限系统(绿线)、固定门限系统(黑线)与本文所提出的系统(蓝、红线)在σ=0.5、σ=0.25、σφ=0.07的大气湍流条件下的仿真误码率曲线。为了保证各系统的总功率相同，我们设理想自适应判决门限系统和固定门限系统的发射功率Pi为1。同时我们设基于动态门限的幅度调制空间相干光通信系统的发射功率Pi以及本振激光器功率Pl为0.5。此外，我们假设固定门限系统的判决门限Tth=0.5。从图中可以看到固定门限系统在大信噪比的区域出现了误码率饱和现象，而本文所提出的系统消除了这种现象。此外，从图中我们还可以看到理想自适应判决门限系统在σ=0.25的大气湍流条件下，需要25.6 dB的信噪比来到达10-9的误码率，而本文提出的系统也只需要27 dB的信噪比来达到相同的误码率。因此本系统在该误码率和大气湍流条件下与理想化的自适应判决门限系统相比仅存在1.4 dB的信噪比差距。

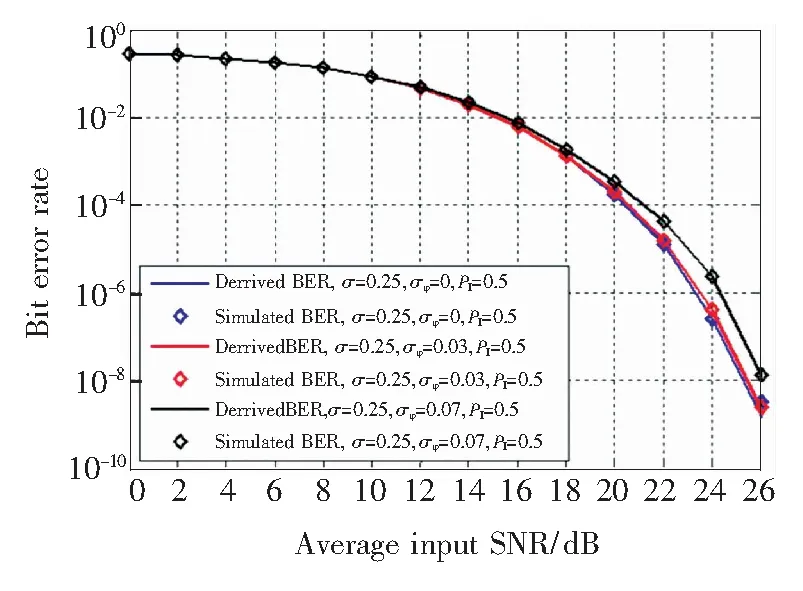
图4 基于动态门限的幅度调制空间相干光通信系统在不同相位噪声下的理论推导及仿真误码率

Fig.4 Derived BERs and simulated BERs of the coherent optical communication system using irradiance modulation with dynamic detection threshold over different phase noise

图4为本文所提出的系统在相位噪声标准差σφ不同的湍流条件下的理论及仿真误码率曲线。为了方便说明，我们假设发射端发射功率与本振激光器功率均为0.5、大气的闪烁标准差为0.25。从图中可知，系统误码率的理论推导值与仿真结果十分吻合。此外，系统的误码率会随着σφ的上升而逐渐恶化，但同时当σφ足够小时(σφ=0.03)，系统的误码率性能与不考虑大气所引入的相位噪声时的误码率性能极为接近。

图5展示了本文所提出的系统在不同的大气湍流条件下使用不同的本振激光器功率时的理论推导及仿真误码率。为了能更好地说明问题，我们设σ=0.25,Pi=0.5。由图5可知系统的误码率性能随着本振激光器功率的提升而变得更好。当我们将本振激光器功率提高1倍时，误码率曲线整体向左移了3 dB。这是由于随着本振激光器功率的提高，系统的输出信噪比也得到了提升。换言之，该系统可以通过提高本振激光器功率的方法来提高系统的探测灵敏度。这一特性十分有利于该系统在诸如卫星通信等发射光功率较低的场景下应用。

图5 基于动态门限的幅度调制空间相干光通信系统在不同的大气湍流条件下使用不同的本振激光器功率时的理论推导及仿真误码率

Fig.5 Derived BERs and simulated BERs of the coherent optical communication system using irradiance modulation with dynamic detection threshold and different LO power over different turbulence channel

5 结 论

本文提出了基于动态门限的幅度调制空间相干光通信系统。实验表明，该系统无需瞬时信道状态信息和大气湍流模型的概率密度函数的辅助就可以达到较好的误码率性能。此外，本文还推导了该系统平均误码率的表达式。仿真实验表明，该系统以较低的复杂度实现了与理想自适应判决门限系统相当的性能，且理论推导与仿真结果相符。因此，该系统有助于自由空间光通信的实现和性能提升。