基于动态规划的双序列比对算法构件设计与实现
2019-09-16石海鹤周卫星
石海鹤 周卫星
(江西师范大学计算机信息工程学院 南昌 330022)
序列比对是一种通过排列基因组序列来识别序列相似性区域,从而获得待比对序列之间的功能、结构或进化关系的技术.随着人类基因组计划的实施,测序技术的发展产生了大量的有关生物分子的原始序列数据,例如,Illumina HiSeqX Ten在3天之内可以产生大约30亿个2×150 bp的双端测序数据[1].面对如此丰富的基因组序列数据,如何高效处理和分析这些丰富的基因组序列数据,如比较两序列之间的相似区域和保守性位点,寻求序列同源结构,揭示生物遗传、变异和进化关系等,成为了序列比对算法研究的主要动力之一.
研究表明,计算机的微处理性能和存储设备容量平均每18~24个月增长1倍,而基因组测序数据则平均4~5月就增长1倍,这成为了高性能计算发展史中一个前所未有的挑战,因此序列比对算法的时空开销和精准度成为生物序列比对过程中的关键因素之一.由于序列比对属于NP-hard问题,而运筹学中动态规划策略多用于解决多阶段决策过程最优化问题,因此,动态规划策略被广泛应用于序列比对算法之中.这里我们主要针对基于动态规划的双序列比对算法(dynamic programming-based pairwise sequence alignment algorithm, DPPSAA)领域开展研究.
在双序列比对算法中最为经典的确定性双序列比对算法有基于全局比对的NW算法[2](Needleman-Wunsch algorithm)、基于局部比对的SW算法[3](Smith-Waterman algorithm)和准全局比对算法.在后续的研究中,发展出了基于以上算法进行优化[4-6]或作为主要比对策略[7-9]的系列算法.
目前,比对算法的研究大部分集中于序列相似性分析领域中的特定问题[10-13]或者特定算法优化[14-16],而较少面向于整个问题域,难以得到一个具有更高抽象层次且适用于整个序列相似性分析领域的算法构件库,在一定程度上导致了序列比对算法的冗余以及人为选择算法可能造成的误差等问题,也使得人们难以有效地了解算法结构,无法保证算法的正确使用,在一定程度上降低了序列相似性分析结果的准确性.由于现有算法的专用性和低抽象性,不仅导致研究人员需要花费大量时间去学习和使用该类算法,降低了算法的可维护性和复用性,而且难以定位和解决算法产生的错误,加重了序列相似性分析的负担.
通过深入分析DPPSAA领域,本文设计和实现了该领域抽象泛型算法构件库,提高了序列相似性分析领域算法可靠性和开发效率.首先对DPPSAA领域进行特征分析,提取出其中的通用和可变特征以及它们之间的约束与依赖关系,建立了一致的领域构件模型,基于此设计了算法构件交互模型,进一步利用新型高可靠软件开发平台PAR[17-19]中高抽象程序设计语言Apla(abstract programming language)进行形式化实现,形成了一个高抽象DPPSAA构件库,以期自动或半自动装配构件产生特定领域序列比对算法,甚至于装配出更为高效的新型序列比对算法.
1 比对算法的建模过程
1.1 领域分析
面向特征的领域分析[20](feature oriented domain analysis, FODA)是由软件工程研究所(Software Engineering Institute, SEI)于1990年首次提出的一种领域分析方法,主要包含上下文分析以及特征建模2个阶段[21].其中上下文分析主要由界定待研究领域需求范围以及领域的输出与输入构成,该阶段的成功实施能够保证特征建模过程中被选取特征的有效性和可靠性.特征建模阶段则包含了特征选取与建立、特征关系描述以及特征模型建立等过程,在该阶段需要对被研究领域进行分析,充分了解其功能性特征和非功能性特征,并找出特征之间的约束和依赖关系以及优先级等附加信息,进而获得该领域的主次要特征,建立一种具有更高抽象层次的特征模型或者构件框架.
特征建模阶段主要包含以下4种特征:强制特征(mandatory)、可变特征(optional)、OR特征、XOR特征.强制特征表示领域内的所有实例都必须包含的特征,可变特征表示领域中实例的一个可选特征,XOR特征表示领域中实例有且只能选择一组XOR特征中的一个特征,OR特征表示领域中实例至少包含了一组OR特征中的一个特征,特征表示如图1所示.特征建模清晰地刻画了特征模型构建过程中所需的各类特征,是识别和捕捉差异性和可变性的关键技术.
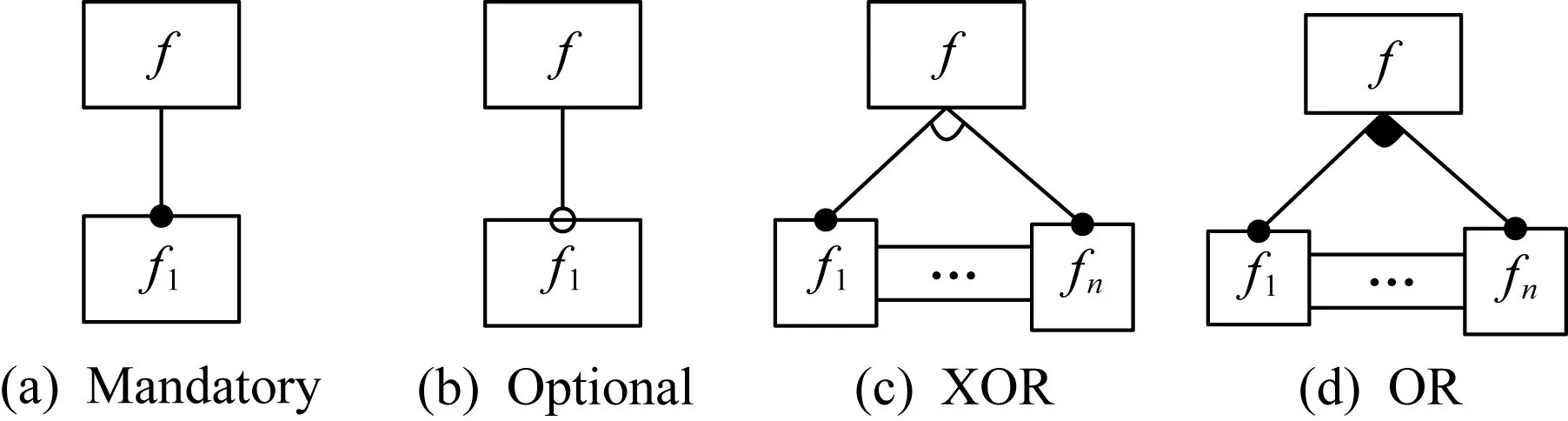
Fig. 1 Feature graph图1 特征图
图1中强制特征被末端为实心圆的边所指向,可变特征被末端为空心圆的边所指向,XOR特征被一组用弧连接的边所指向,OR特征被一组用实心弧连接的边所指向.这4种特征是特征建模中的主要属性,也是特征模型的重要组成部分,代表了领域中的通用和可变属性,同时它们之间的约束以及依赖关系则需通过特征内在的层次结构关系、领域业务逻辑设计的约束关系以及运行时依赖关系来表示.
1.2 特征建模流程
以FODA为基础,我们在其后增添了领域实现阶段,即将建立的特征作为构件进行构件交互模式设计和形式化实现,建立抽象构件库.需要注意的是,由于建立的构件之间的交互性,程序人员使用C,C++或Java等低抽象层次高级编程语言进行代码编程时,不仅增加了特征之间的关联性与复杂性,而且难以让使用者对整个构件库有具体和全面的了解.因此需要使用一种具有高抽象性的编程语言来实现这些构件,以至不用在意算法构件的具体实现细节,而能够清晰地了解这些算法构件的功能以及它们之间的交互关系.例如在本文中主要利用Apla语言来实现DPPSAA领域构件.
基于以上介绍,对具体领域进行分析时,领域构件库建立流程图如图2所示:

Fig. 2 Flow chart of domain analysis图2 领域分析流程图
1.3 DPPSAA领域特征建模
特征模型描述了领域内实例的通用和可变特征以及它们之间的约束与依赖关系,是在特征建模过程中构建的,一般由描述特征层次关系的特征图和相关的文本描述组成.其中特征图通常使用具有不同层次的树状结构来表示,在该结构中包含了1组节点、1组节点之间的定向边以及两边之间的关系描述.其中1个节点代表一个特征,具有唯一的标识符;节点之间的定向边将特征连结成树结构;两边之间的关系描述则代表特征之间的关系,是对特征节点的划分.同时特征模型中的文本描述则表示了特征的语义描述、原理以及约束和默认依赖规则等信息.
因此,针对基于动态规划的双序列比对算法领域,建模过程有3方面:
1) 上下文分析.该算法领域的范围被限制为一种在生物序列相似性分析领域中以动态规划为主要罚分策略、双序列比对为主要比对方式的算法形式.
2) 特征建模.我们利用特征建模方法[22]对该领域进行特征建模,即从分析领域中的服务(service)、功能(function)以及行为(behavior)特点入手构建特征模型.比对操作服务是该领域中的核心服务,通过控制序列比对过程中的比对方式和各算法特征之间的执行优先级以及组合方式来实现使用者定义的序列比对算法.通过分析双序列比对算法中的一些主要执行步骤,可以将该比对操作服务进一步划分为检查序列合法性、得分矩阵操作、动态规划算法方式选择、记住得分来源、回溯和比对结果输出等功能,同时得分矩阵初始化、动态规划方式选择以及检查序列合法性作为3个必选的功能.在上述分析的基础上,输出方式是比对结果输出的显著行为特点,包括比对序列输出和比对得分输出两种主要行为特点,且二者属于OR特征.动态规划方式可以分为全局动态规划方式、准全局动态规划方式、局部动态规划方式3种,三者为XOR特征.我们根据上述分析对该领域建立了特征模型,如图3所示:
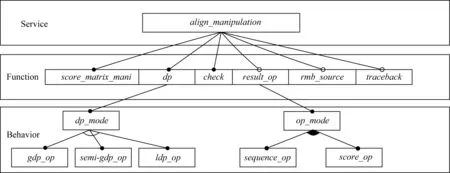
Fig. 3 DPPSAA feature model图3 DPPSAA特征模型
3) 领域实现.该过程针对已建立的特征模型进行DPPSAA领域算法构件交互设计并使用Apla语言形式化实现.
2 比对算法构件的设计与实现
2.1 DPPSAA领域算法构件交互设计
不同构件通过交互实现完整的算法构件库,而算法构件的交互则需要由其包含的特征之间的约束以及依赖关系来体现.因此针对1.3节建立的特征模型,我们对DPPSAA领域的算法构件交互模型进行了设计.
通过分析整个DPPSAA领域得知,算法主要包括3个主要变化过程特征:得分矩阵操作、动态规划算法方式以及比对结果输出.因此,我们将特征模型中的这些特征以及检查序列合法性作为主要构件,其他特征以及相关数据结构作为辅助构件,并根据其优先级建立了构件间的交互模型,如图4所示:
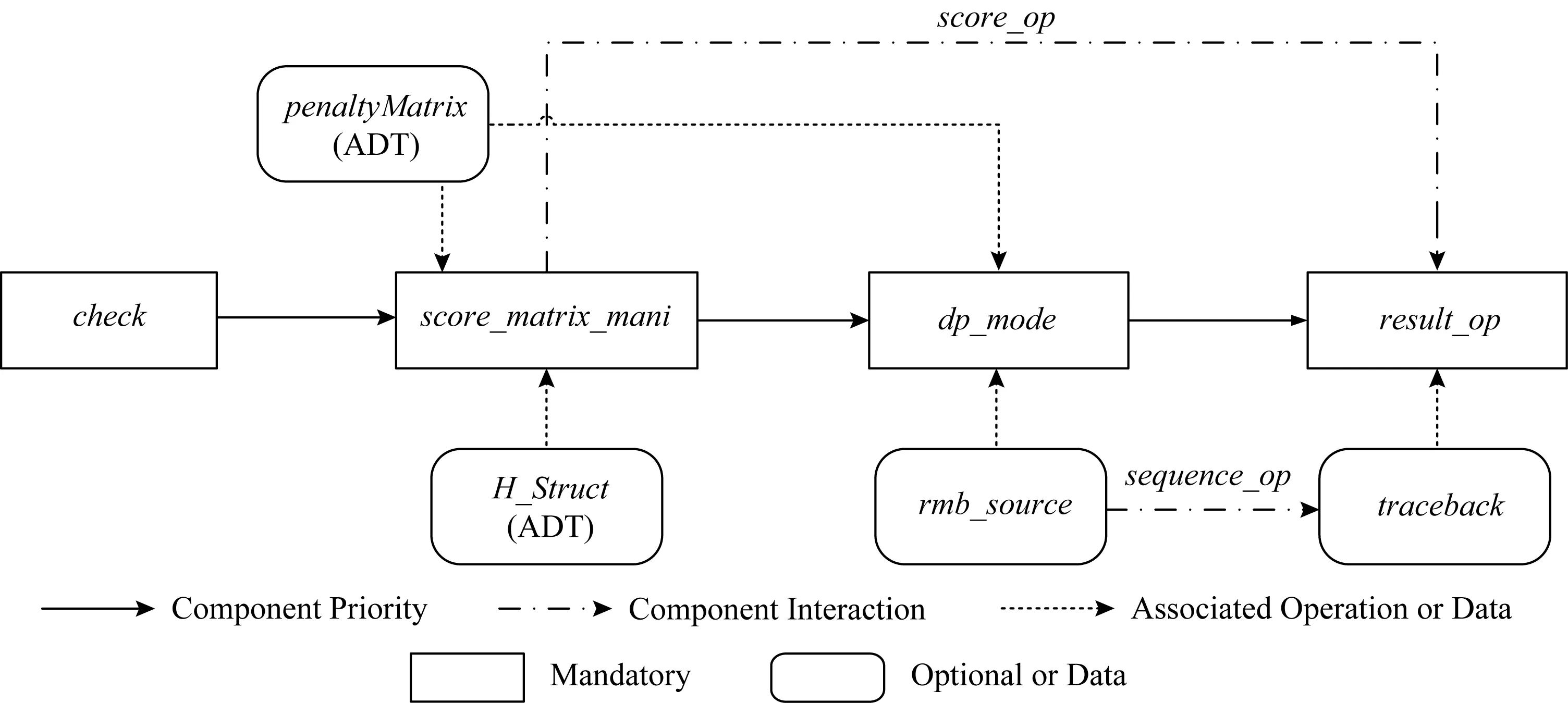
Fig. 4 Algorithm components interaction model图4 算法构件交互模型
图4中实线所连接的节点表示为DPPSAA领域中所必须含有的基本构件,即对应于特征模型中的4个强制特征,实线箭头所代表的方向表示4个构件的执行优先级为由高到低;点连线箭头表明在算法执行过程中2个构件之间的交互,如在图4中,当比对结果输出构件选择得分输出时,则需要使用得分矩阵操作构件中的获取元素得分操作;虚线箭头则代表在算法组装过程中所需的数据、结构以及关联操作等,如在得分矩阵操作构件中需要使用2个抽象数据类型(abstract data type, ADT):罚分模型ADT和得分矩阵元素ADT,且罚分模型ADT同时作用于动态规划算法方式构件等.
2.2 Apla形式化实现
Apla语言可以直接使用抽象数据类型和抽象过程编写程序,因此能够更抽象地描述算法问题,并易于对其进行正确性验证,保证了程序正确性和可靠性.
PAR方法和PAR平台包含循环不变式的新定义和新的开发策略、统一的算法程序设计方法、新的算法表示方法、自定义算法设计语言和抽象程序设计语言等关键技术.它集成涵盖了泛型、生成式、模型驱动和构件组装等新型软件开发技术,其系列程序自动生成系统可将一个正确的Apla程序自动转换成C++,Java,Delphi等高级语言程序.因此,本文利用该语言形式化实现并建立了DPPSAA领域算法构件库,不仅可高抽象表示算法程序的功能特性与非功能特性,而且能够直观地展示各算法构件之间的约束以及依赖关系.这样既减少了各构件之间的干扰,降低了算法程序的复杂性,提高了算法构件安全性,又消除了传统算法设计方式中算法与数据难以分离的问题,提高了构件装配产生算法的可复用性和可维护性,同时使用该算法构件库时,我们只需关注算法功能即可,而不用在意具体构件实现细节,从而提高了算法设计效率.
下面展示了对DPPSAA领域构件的Apla程序实现.
1) 罚分模型以及得分矩阵元素结构设计
首先我们将罚分模型设置为一个ADT,这里我们为解释方便,只使用固定空位罚分策略,与扩展罚分时操作类似.其中罚分模型的ADT定义为
define ADTpenaltyMatrix(sometypeelem);
match:integer;
mismatch:integer;
space:integer;
enddef.
其中sometype为Apla语言中的关键字,用来定义类型变量.其中的match,mismatch,space分别表示罚分模型中的匹配罚分值、错配罚分值以及空位罚分值.
在得分矩阵中,由于序列比对结果输出时需要进行回溯操作,因此我们将得分矩阵中的元素定义为一个ADT,命名为H_Struct,该ADT中包含了整型变量value和boolean型的数组dp_direct,前者表示2个字符比对得分值,后者表示该得分值的来源(其中true代表对应得分来源为真,false代表为假).并且数组内的元素含义如图5所示,4个方框分别代表得分矩阵中的4个元素,3个箭头分别表示(i,j)中的得分来源为上、左和对角元素,分别用数组dp_direct下标0,1,2对应的数组元素来表示.
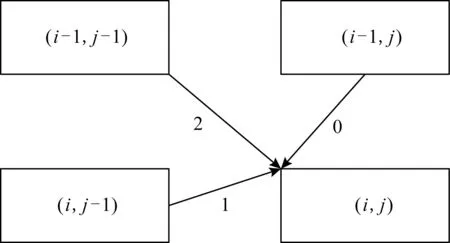
Fig. 5 Score source of score matrix element图5 得分矩阵元素的得分来源
该ADT定义为
define ADTH_Struct(sometypeelem);
value:integer;
dp_direct:array[0:3,boolean];
enddef.
2) 得分矩阵操作
该构件被定义为一个ADT类型,因为在不同的DPPSAA中得分矩阵初始化方式不同,因此在该ADT内部包含了一个泛型子程序Memory_Score_of_Matrix,并将Init_score_matrix方法作为它的泛型参数,使得泛型子程序可以支持实例化具有不同得分矩阵初始化方式的比对算法,即当使用不同的方法参数实例化Init_score_matrix时,将返回不同的得分矩阵.同时在该ADT中还包含了一些常用的得分矩阵操作,如求矩阵最大得分、矩阵元素取值操作和赋值操作等.
define ADTscore_matrix_mani(sometypeelem);
procedureapply_memory(length_s:integer,length_t:integer);
procedureMemory_Score_of_Matrix(procInit_score_matrix());
functionMax_score_of_Matrix:integer;
functionthe_Last_element_score:integer;
functionget_value(i:integer;j:integer):integer;
procedureset_value(i:integer;j:integer;score:integer);
enddef.
其中该ADT类型名为score_matrix_mani,且带有一个类型参数elem;apply_memory泛型子程序的作用是根据整型变量length_s和length_t值为score_matrix_mani动态分配内存空间;函数Max_score_of_Matrix和the_Last_element_score分别表示获取score_matrix_mani中得分最大值以及最后一个元素的得分值;get_value以及set_value分别为获取和设置score_matrix_mani中元素得分值,(i,j)(0≤i≤length_s,0≤j≤length_t表示对应元素的下标,length_s和length_t分别表示两比对序列的长度.
3) 动态规划算法方式选择
该构件也被定义为泛型ADT,可以支持不同的序列比对算法所使用的动态规划得分模式,得分模式的变化主要依靠泛型子程序dp_align_score来实现,同时该ADT类型中还包括求2字符的最大比对得分操作max_score_of_char,函数中的3个参数分别表示不同来源的罚分值.
define ADTdp_mode(sometypeelemMatrix);
functionmax_score_of_char(up_score:integer;left_score:integer;diag_score:integer):integer;
proceduredp_align_scores(s:String;t:String;sM:penaltyMatrix;procset_and_remember(sometypeelemMatrix;length_s:integer;length_t:integer));
enddef.
这里elemMatrix是一个类型参数;函数set_and_remember是泛型子程序dp_align_score的泛型参数,该函数的功能为记录得分矩阵中各元素的得分值以及得分来源,可以被用于各种动态规划罚分模型的实例化.
4) 检查序列合法性
检查序列是否属于字符集{A,T,C,G}(默认为DNA序列,如果为其他序列,加入对应表示字符即可,如果为RNA序列,则将G换为U即可).
procedurecheck(s,t:String).
其中s和t都为字符串类型.
5) 记住得分来源
该构件表示记住(i,j)处得分的来源,即将(i,j)处中对应的方向标志赋值为true.其为回溯阶段输出序列比对结果提供支持.
procedurermb_source(i:integer;j:integer).
6) 回溯
该构件的Apla语言定义为
proceduretraceback(procprint_align();procprint_extrude()=NULL).
在回溯过程中,一般由短序列比对区间回溯和两端突出回溯组成,其中短序列比对区间回溯表示从2序列匹配的第1个序列字符开始,到最后匹配的字符结束位置之间的字符区间序列输出,两端突出回溯则表示从头开始到第1个匹配字符的前一个字符区间序列输出或者最后一个匹配字符的下一个字符到最后所有字符序列对应输出.在trackback泛型子程序中分别由print_align和print_extrude表示,并且在默认配置下print_extrude为空,即为全局比对.
7) 比对结果输出
这里将该构件定义成一个泛型子程序.
procedureop_mode(funcfinally_score():integer;proctraceback(procprint_align();procprint_extrude()=NULL)).
在此泛型子程序定义中,函数finally_score功能为输出最终比对得分.
8) 比对操作
为了能够实现现有的序列比对算法,需要对上述算法构件进行人工装配,因此将比对操作服务定义为一个泛型子程序,并将各功能作为其参数,使之能够支持装配产生DPPSAA.
procedurealign_manipulation(op_mode(funcfinally_score():integer;proctraceback(procprint_align();procprint_extrude()=NULL));ADTdp_mode(eM:elemMatrix);sometypeelemMatrix;result:boolean;eM:elemMatrix;s:String;t:String)).
该算法构件align_manipulation主要包含4个参数:比对输出构件op_mode、回溯构件traceback、自定义泛型ADTdp_mode以及待比对序列s和t.其中elemMatrix表示为一个类型参数,并且后面4个变量参数为在主程序中实例化参数所需代入的.这样我们就可以通过手工装配该子程序,以达到实现相应比对算法的目的.
3 NW算法的装配实现
通过第2节的介绍,可以较清晰地了解到整个DPPSAA领域构件库的建立过程,下面我们利用上述构件库来装配实现基于全局的双序列比对算法NW,程序为
program para;
const
procedureInit_score_matrixNW(sometype
elemMatrix);
①
var
i,j:integer;H:elemMatrix;
begin
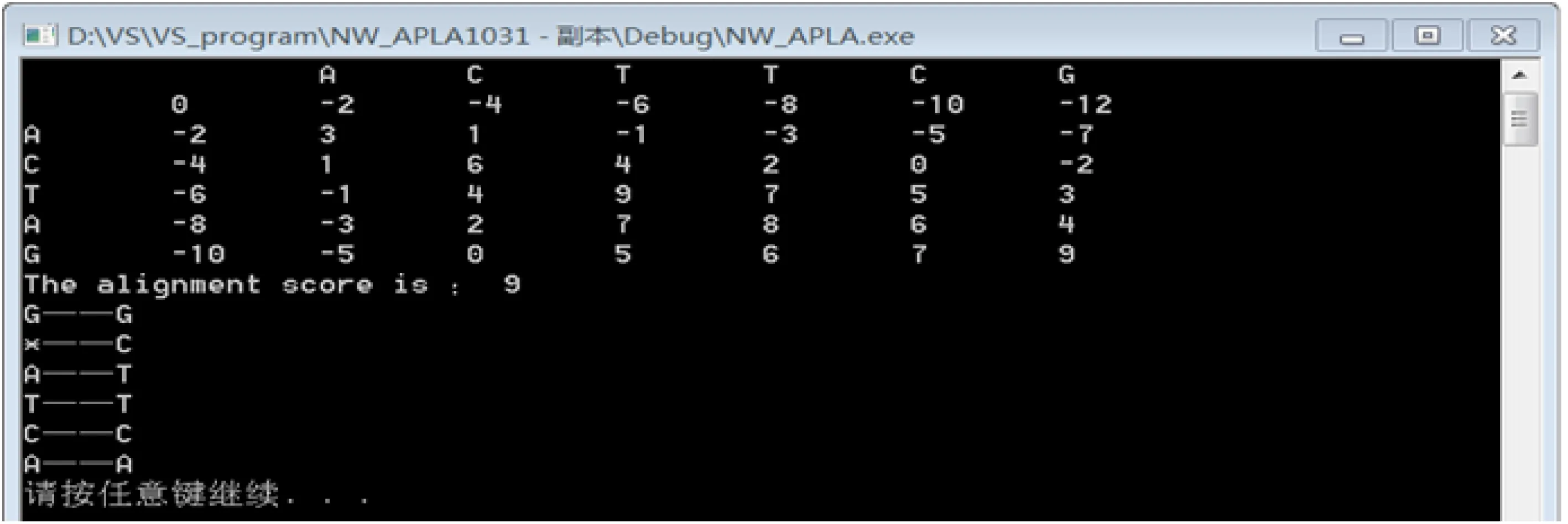
foreach(i,j:0≤i,j length_t:…;); ② end; procedureset_and_remember(length_s: integer;length_t:integer;sometype elemMatrix); ③ var i,j:integer; begin foreach(i,j:0≤i,j length_t:…;); ④ end; ADTpM:newpenaltyMatrix(); ADTstruct:newH_struct(); ADTmatrix:newscore_matrix_mani(struct); ADTdp_NW:newdp_mode(matrix); var dp_g:dp_NW; begin dp_g.dp_align_score(matrix,set_and_ remember(sometypeelemMatrix; length_s:integer;length_t:integer)); ⑤ end; procedurealign_manipulation(sometype elemMatrix;ADTdp_mode(eM:elemMatrix); op_mode(funcfinally_score():integer; proctraceback(procprint_align(); procprint_extrude()=NULL); result:boolean;eM:elemMatrix; s:String;t:String); ⑥ begin if(result) write(“The alignment score is:”, finally_score()); else traceback(print_align,print_extrude); end; procedureNW:newalign_manipulation(score_matrix_mani,dp_g,op_mode(print_align)); ⑦ begin ⑧ check(s,t); matrix.apply_memory(s.length(), t.length()); matrix.Memory_Score_of_Matrix(Init_ score_matrixNW(matrix)); NW(false,matrix,s,t); end. 在上面程序中,过程①为得分矩阵初始化的不同实例化方式;代码块②和④由于得分矩阵初始化过程占用篇幅过大,因此用…表示;过程③则为记录比对得分值以及得分来源的实例化;⑤则表示NW算法的动态规划算法的实例化;泛型子程序⑥则表示在步骤⑦实例化NW算法对象时内部所要执行的算法构件间的关联操作;⑧以下的代码块为主程序. 目前,由于Apla语言无法在PAR平台上直接运行,本节利用PAR平台C++程序生成系统,将组装NW算法过程中所需的Apla算法构件代码转换为相对应的C++代码. Apla代码中只包含数据成员的ADT算法构件被转换为C++中的结构体,如penaltyMatrix以及H_Struct等,其结果为 structpenaltyMatrix { intmatch; intmismatch; intspace; }; structH_Struct { intvalue; booldp_direct[3]; }. 含有数据成员和成员函数的ADT则被转换为C++函数中的类,如score_matrix_mani,dp_mode等,其中大括号内的省略号表示函数体,且Sequence类将2个待比对序列作为其数据成员.其转换的部分结果如图6所示. 同时,Apla代码中的泛型子程序和泛型函数等被转换为C++中独立的类成员函数,降低构件间的耦合性.其中,主调函数与主调函数泛型参数之间的关系被转换为C++中的函数指针,即将泛型参数转换为主调函数的指针函数参数,从而具有与Apla程序同样的多态性特征,如traceback泛型子程序的C++转换结果如图7所示. 可将Apla算法构件代码转换成可执行的C++代码,最后利用转换后的算法构件进行手工装配NW算法(即将服务align_manipulation转换为主函数)如图8所示,并输出代码结果如图9所示. Fig. 6 Result of ADT transformation图6 ADT转换结果 Fig. 7 Result of generic program transformation图7 泛型子程序转换结果 Fig. 8 C++ assembly process of NW图8 NW的C++装配过程 Fig. 9 NW alignment result图9 NW比对结果 在PAR平台的支撑下,我们以半自动的方式将上述Apla语言编写的DPPSAA算法构件程序转换成C++代码,并装配形成NW算法.经实际运行NW算法检测,算法的运行结果与原本NW算法结果一致.使用DPPSAA领域构件装配形成的具体双序列比对算法,不但提高了装配算法程序的可靠性、执行效率以及可维护性,而且可以根据客户需求进行手工装配形成指定算法,增强了DPPSAA算法构件的通用性. 在下一步研究工作中,为实现自动化装配DPPSAA领域算法,我们将使用产生式编程的相关方法学来开展工作,为进一步装配生成奠定了基础,可望装配形成一种相较于现有算法具有更高执行效率和更低内存消耗的新型双序列比对算法. 针对序列比对算法研究的不同方面,国内外学者通过使用并融合相关方法学技术开展了较多研究工作,可分为3个方面: 1) 基于代数方法的研究.比勒费尔德大学的Giegerich等人[23-25]提出了一种面向系统族的基于代数结构的新型动态规划构造算法,通过利用代数数据类型概念将动态规划算法过程形式化定义为2个阶段:识别阶段和评价阶段.在具体应用过程中,算法通过迭代进行这2个阶段,可为序列比对算法领域内待生成算法提供一种更具一般性的生成范式,简化了算法开发过程,提高了生成算法的正确性和可靠性. 2) 基于有限状态机的研究.宾夕法尼亚大学的Searls等人[26]提出了一种基于有限状态机和具有自适应加权的序列比对算法生成方法.该算法利用有限状态机模型形式化表示序列比对过程中的罚分、比对以及动态规划过程,并对比对过程中的不同碱基字符比对结果(匹配、错配以及空位)进行自适应加权,能够快速地生成新型序列比对算法.算法能够支持可视化编程. 3) 基于算法优化的研究.算法优化是指为了提高已有算法处理问题能力而进行研究的过程.文献[27]采用经典的脉动阵列结构的并行加速器体系结构来提高序列加载、比对和结果收集效率的数据通路,并且利用Hash索引优化技术过滤比对过程中的非相似行序列,增强了序列比对算法的性能.为了提高序列比对算法的准确度,文献[28-29]等利用改进的隐马尔可夫模型对序列比对算法进行优化. 序列比对作为生物序列分析中的关键问题,其算法及应用研究受到广泛关注,然而,尚未有工作将其视为一个专门领域从高抽象层次开展研究,从而提高算法可靠性和开发效率、降低算法次优解及误差等问题出现的概率.我们采用特征建模,分析和提取出基于动态规划双序列比对算法领域的通用以及可变特征,并利用高抽象语言进行形式化实现,以期能够以自动或者半自动方式进行形式化组装生成特定问题的求解算法,从而降低人工选择算法进行序列相似性分析的错误发生率以及时间开销,提高算法执行效率,甚至于装配出一种更为高效的基于动态规划的新型序列比对算法. 本文首先提出了一种领域建模过程,包括上下文分析、特征建模以及领域实现3个主要阶段;其次通过分析DPPSAA领域的一般执行过程,抽取出算法的通用以及可变特征,并建立领域特征模型;然后对建立的构件特征模型进行构件交互设计,同时利用Apla语言形式化实现这些算法构件,并通过手工装配生成了NW算法实例;最后利用PAR平台C++程序生成系统将Apla程序转换为C++可运行程序,转换结果以及算法运行结果展示了其具有一定的实用性.由于Apla的高抽象性,建立的一系列泛型构件,如dp_mode,result_op等,保证了构件装配后的算法多样性,也能够较好地展示出算法特征之间的联系. 我们对整个DPPSAA领域进行了精确分析,对其各功能特性与非功能特性有充分的了解,同时在算法设计过程中建立了特征模型以及构件交互设计,从而有利于算法构件库的学习和使用;另外,使用高抽象语言Apla形式化实现算法构件,不仅易于对Apla算法程序进行正确性验证,保证算法构件库的可靠性,而且在使用过程中可利用泛型编程机制快速发现和定位算法中的错误,提高算法构件库的鲁棒性. 本文研究DPPSAA领域的主要方法学思想和成果,不仅适用于DNA序列比对算法,理论上对于一些其他的生物序列分析算法领域也具有参考价值和实用价值,例如基因组装过程中的基于de bruijn graph结构的组装算法[30-32].下一步的研究尚需扩充本文结果在生物序列分析算法领域的应用范围,同时基于PAR平台实现算法构件库的自动或半自动装配.4 实验及其结果分析



5 相关研究比较
6 结束语
