车联网蠕虫的随机传播模型*
2019-09-14周翰逊冯润泽熊俊坤
周翰逊,杨 阳,冯润泽,熊俊坤,万 明,郭 薇
1.辽宁大学 信息学院,沈阳 110036
2.沈阳航空航天大学 计算机学院,沈阳 110136
1 引言
随着信息技术的不断发展以及数据量的激增,人们迫切地需要将客观世界的物体与网络相连,因此产生了物联网产业[1-3]。自从物联网纳入到国家十二五规划中,物联网技术得到了国家的大力扶持也得到了迅猛的发展。作为物联网的重要领域——车联网也得到了学术界以及商业界的重视[4]。目前,百度、阿里巴巴、腾讯等公司已经推出了车联网相关产品。然而,在车联网得到蓬勃发展的同时,人们对于车联网中的安全问题也越来越关注。一旦车联网遭到恶意攻击,将会给人和车辆的安全造成严重威胁。
车联网蠕虫作为车联网的重要安全问题之一,也引起人们广泛关注。由于构建网络蠕虫的传播模型可以揭示其传播的内在规律[5-9],因此人们试图对其进行数学建模。文献[10]首次对于在高速公路传播的网络蠕虫进行了分析。然而,该方法不能考虑V2V(vehicle-to-vehicle)的动态特性并且高估了网络蠕虫在高速公路中的传播速度[11]。文献[12]提出了影响蠕虫在道路上传播的重要参数,即通信范围、车辆密度以及介质访问控制机制等。文献[13]研究了蠕虫在大规模道路网络中的传播动态特性,并且发现蠕虫可以在几分钟内就感染大量道路上具有漏洞的车辆。然而,如上工作只是通过仿真工具研究了网络蠕虫在车联网中的传播特性,并没有提出准确的数学模型对车联网中的蠕虫传播进行建模。
本文基于随机过程理论对车联网中蠕虫的传播进行了数学建模。在没有安全防护软件的理想情况下,基于Galton-Watson 分支过程对车联网蠕虫进行了建模;在具有安全防护软件的现实情况下,当高速公路车流符合泊松分布时,基于排队论对车联网蠕虫进行了建模,并且研究了其稳定性条件。当高速公路车流符合正态分布时,基于马尔可夫链对车联网蠕虫进行了建模。最后,通过仿真实验验证了提出的车联网蠕虫传播模型。
2 车联网蠕虫
车联网蠕虫是指利用车载计算机及其他电子设备嵌入式平台存在的安全漏洞而在车联网中传播的网络蠕虫,对于在车联网中的车辆安全驾驶构成严重的威胁。目前的车联网可以划分为V2V 和V2I(vehicle-to-infrastructure)两种形式[8]。V2V是指车与车之间可以互相通信,能够让相互靠近的汽车之间互相发送诸如位置、速度以及行驶方向等基本的安全信息,从而大大减少汽车碰撞事故的发生概率并缓解交通拥堵。V2I 是指汽车与道路基础设施进行通信,汽车可以通过道路基础设施交换道路基本信息,甚至连接其他网络。由于V2I不容易受到攻击[8],因此本文主要研究V2V下的车联网蠕虫的传播规律。
经典的网络蠕虫如扫描蠕虫,可以在短时间内感染全世界接入互联网的具有该蠕虫可以感染的所有漏洞主机,但是由于目前V2V 通信的最大范围为300 m,因此车联网网络蠕虫只能感染离感染车辆最大范围为300 m 内的车辆。在车联网中,由于诸如SAE J2735 等V2V 通信标准均支持在高频段中周期性广播信标消息,因此车联网蠕虫可以很容易地收集车辆的相关信息并且找到具有漏洞的车辆进行攻击。车联网蠕虫的攻击策略可以划分为攻击所有的漏洞车辆,或者为了避免被人们发现选择性地攻击传播范围内的一辆漏洞车辆两种。图1 为车联网蠕虫选择性攻击一辆漏洞车辆的攻击示意图。车A攻击具有漏洞的车B成功后,车B又对于具有漏洞的车辆C进行攻击,以此类推,完成车联网蠕虫的攻击过程。

Fig.1 Worm propagation in Internet of vehicles图1 车联网蠕虫的传播
3 车联网蠕虫的随机传播模型
3.1 车流模型
在讨论车联网蠕虫传播模型前,先讨论公路上的车流模型。首先,考虑单车道的车流模型。假设在单位时间车辆的到达概率为p,具有蠕虫可以感染的漏洞车辆率为r时,在单位时间内到达具有蠕虫可以感染的漏洞车辆为k的概率为:
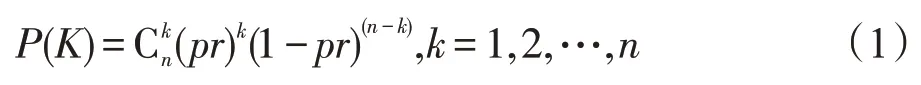
其中,n为V2V 通信的最大范围内容纳的车辆数。由于目前V2V通信的最大范围为300 m,汽车的最短车长3 m,因此在单车道300 m 的范围内最大容纳的车辆数为100 辆。由于国内标准城市干道每条机动车道3.5 m,因此300 m 的范围内可以有85 条车道。如果有j条车道,那么V2V 通信的最大范围内容纳的车辆数n为100×j,j≤85。
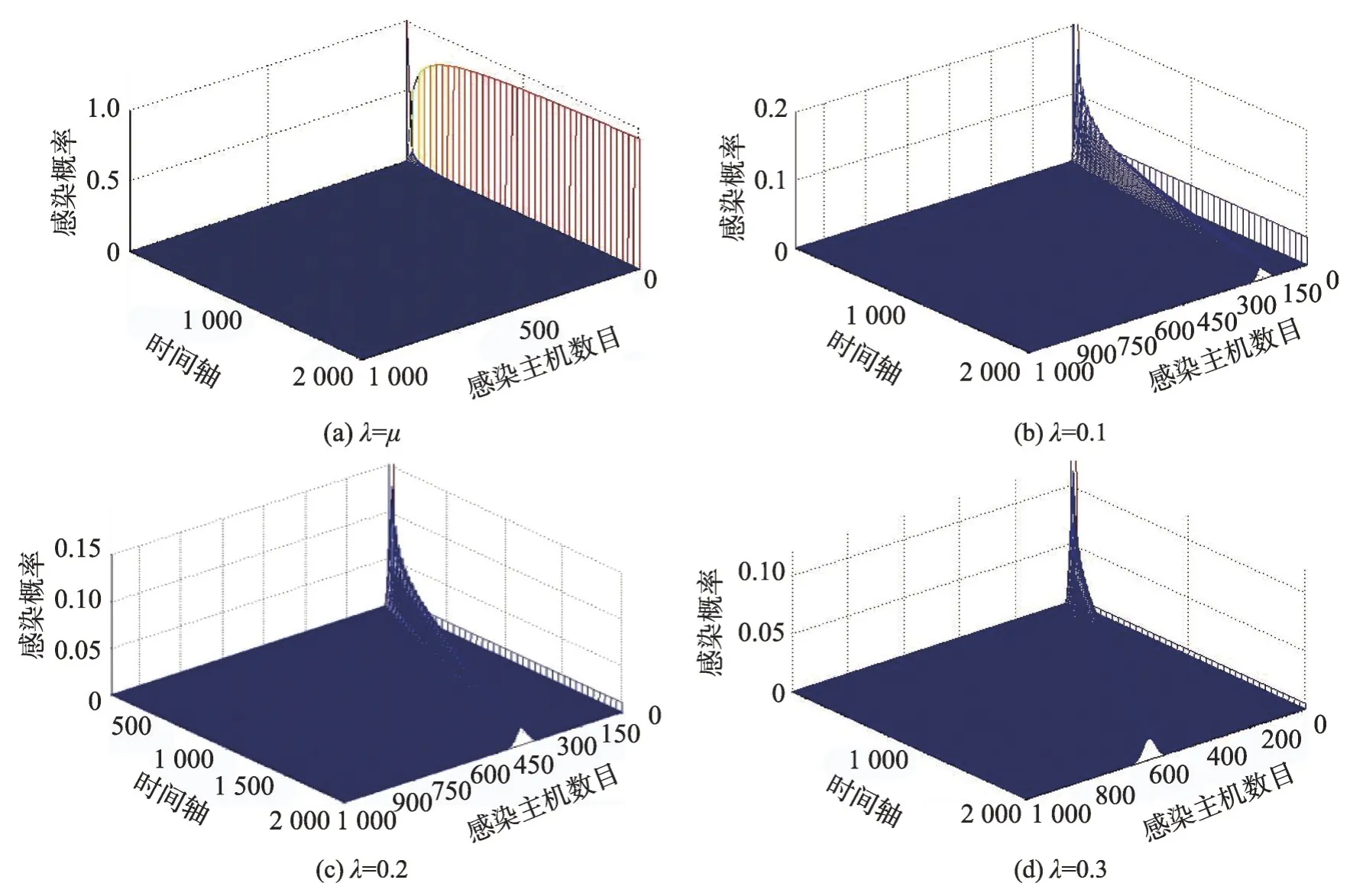
当车辆到达概率较小时(可以近似看作车辆的平均流速较小),也就是p×r较小时(0 然而,由于不同国家人们驾车习惯或者文化的不同,车流的模型可能会有所差异[14]。文献[14-15]对上海的高速公路上的车流进行分析,发现其更符合正态分布: 其中,μ为车流平均值,σ2为车流的方差。 下面研究i个车道的具有蠕虫可以感染的漏洞车流模型,若车流中具有蠕虫可以感染的漏洞车辆率为r,那么在i条车道中,单位时间内到达的漏洞车辆数X: 因此,X~N(p×(r×100×i),(r×100×i)2σ2)。 如果感染车辆攻击全部漏洞车辆,那么其符合上文所述的泊松或者高斯分布;如果感染车辆选择性攻击一辆车辆,那么其符合0-1分布,如下: 其中,p为漏洞车辆大于等于1 的概率(无论车流符合泊松或者高斯分布,都可以很容易计算该概率0 由于车联网对于安全威胁,尤其是车体客户端蠕虫的安全威胁的处理机制并不成熟[8],而且蠕虫在车联网中传播得又相当快,因此本节主要研究在没有蠕虫查杀的情况下,车联网蠕虫的随机传播模型。车联网蠕虫可以感染的车辆可以划分为感染类和易感类。其中,易感类为车联网蠕虫可以感染的具有漏洞的车辆,感染类为已经被车联网蠕虫感染的车辆。车联网中跟蠕虫传播相关的车辆只能处于感染类或者易感类,易感类可以被车联网蠕虫感染而转化为感染类主机。 3.2.1 基于Galton-Watson 分支过程的车联网蠕虫传播模型 Galton-Watson分支过程描述第n代个体独立同分布的感染第n+1 代个体的数学模型。在车联网蠕虫的传播过程中,在车联网中首先植入的蠕虫为第0代车联网蠕虫,其直接感染的车联网蠕虫为第1代车联网蠕虫。以此类推,第n代车联网蠕虫可以感染第n+1 代车联网蠕虫,由于每代蠕虫独立地感染下一代的蠕虫,因此其感染具有独立性。通过3.1节的讨论,假设车联网蠕虫可以感染300 m内的所有漏洞车辆(3.3 节讨论仅感染300 m 内的一辆漏洞车辆),因此第n代蠕虫感染第n+1 代蠕虫数目服从均值和方差均与车流相关的泊松或者高斯分布。虽然车流在一天的时间里是变化的,但是由于车联网蠕虫的传播时间相当快,如10 min。因此在如此短的时间内,可以近似车流为恒定不变的,车联网蠕虫的第n代感染第n+1 代蠕虫数目服从同分布。又由于车联网蠕虫的感染是独立感染不进行互相协作,因此车联网蠕虫的第n代个体独立同分布地感染第n+1 代个体,因此其符合Galton-Watson分支过程。 令Yn为车联网蠕虫传播到了第n代,Y0为车联网蠕虫最初的感染主机数目。由于在车联网蠕虫传播的过程中,每代蠕虫感染其下一代是相互独立的,并且具有相同的概率分布。第n代新感染的主机为第n+1 代,令为在第n代中被感染的第k个主根据不同路况情机,那么第n+1 代主机况服从泊松分布或者高斯分布。由此可知,只要给定Yn,那么Yn+1的分布就完全决定了,且与以前的Yn-1,Yn-2…无关,故{Yn,n≥1}也是一个马氏链。定理1给出了其状态转移概率的计算方法。 定理1车联网蠕虫的Galton-Watson 分支过程{Yn:n=0,1,…}的一步转移概率矩阵为: 其中: 证明设F(s)是随机变量Yn的母函数,母函数的定义为: 由于车联网蠕虫感染的后代车辆数目服从的概率分布密度已知,因此很容易得到相应的概率分布为: 又由于母函数有如下性质:(1)Y的母函数与其分布率是一一对应的,且有;(2)设非负整值随机变量Y1,Y2,…,Yn相互独立,而g1,g2,…,gn分别是它们的母函数,则的母函数为:gY(s)=g1(s)g2(s)…gn(s)。因此,将其概率母函数带入式(6)得: 因此,可以得到如下等式(10): 由于当i=0 时pij=ρ0,j,因此定理得到了证明。 □ 从定理1 中不难发现:p00=1,p0k=0(k>0)。因此,状态0 是车联网蠕虫的Galton-Watson 分支过程的吸收状态。在车联网蠕虫的分支过程模型中,最关心的问题是此过程被状态0吸收的概率,即灭绝概率问题。下个小节将详细讨论。 3.2.2 灭绝概率 对于车联网蠕虫的Galton-Watson 分支过程模型,灭绝概率P{Yn→0}即对于过程{Yn,n=0,1,…},给定Y0=1 时,第n代有0 个车联网蠕虫的概率=P{Yn=0|Y0=1}的极限。 定理2若车联网蠕虫传播的分支过程为对于攻击传播范围内所有的漏洞车辆的车联网蠕虫,其灭绝概率为1,当且仅当r×300×i×p≤1;对于选择性地攻击传播范围内的一辆漏洞车辆的车联网蠕虫,其灭绝概率为1,即必将灭亡。 证明令车联网蠕虫感染后代的均值为若Y0=1,下面计算E(Yn)和Var(Yn)。首先,可以写出,Yi表示第n-1代车联网蠕虫的第i个蠕虫感染后代的个数。因此: 其中,E[Yi]=μ。由于E[Y0]=1,由式(11)可以得到如下结论: 如果以π0记总体最终的灭绝概率,因此: 若μ<1,则π0=1。这是因为: 由于当μ<1时μn→0,因此P(Yn≥1)→0,P(Yn=0)→1,即π0=1。同理,很容易证明当μ=1 时,π0=1。 如果车联网蠕虫攻击传播范围内的所有漏洞车辆,无论车流符合泊松还是高斯分布,其均值μ都为r×300×i×p,因此r×300×i×p≤1;对于选择性地攻击传播范围内的一辆漏洞车辆的车联网蠕虫,由于每代车联网蠕虫的传播符合0-1 分布,其均值μ为p,而且0 从定理2 中不难发现如果车联网蠕虫选择性地攻击传播范围内的一辆漏洞车辆,其必将灭亡,这违背了蠕虫攻击的初衷,因此车联网蠕虫选择攻击传播范围内的所有漏洞车辆的意义更大。从定理2 可知,选择攻击传播范围内的所有漏洞车辆的车联网蠕虫灭绝的充要条件为p≤1/(r×300×i)。由于车流p,V2V 的传播范围为300 m 以及车道数目i都是无法人为干预的,因此人们只能通过将具有漏洞的车辆进行打补丁降低漏洞率r,才能使得车联网蠕虫最终灭绝。从定理2也可以得知,无论车流服从泊松分布还是高斯分布,其灭绝概率与其分布没有关系。由于选择性地攻击传播范围内的一辆漏洞车辆的攻击策略终将灭绝,因此下面主要讨论选择攻击传播范围内的所有漏洞车辆的车联网蠕虫。 由于没有考虑人们对于蠕虫查杀的情况,因此车联网蠕虫的Galton-Watson分支过程模型可以准确地描述车联网蠕虫传播初期或者当车联网由于发展不完善缺乏对于车联网蠕虫查杀的软件情况。然而,随着车联网发展的日趋成熟,车联网蠕虫的传播将受到人们的控制,该模型将不再适合车联网蠕虫传播的后期,但是该模型的结论是车联网蠕虫传播的极限情况。 随着车联网发展得不断成熟,对于安全问题的解决将日趋完善,人们对于车联网蠕虫传播的抑制也将越来越严格,因此不能不考虑尤其蠕虫传播后期人为干预对于车联网蠕虫传播的影响。车联网中蠕虫可以感染的车辆可以划分为感染类、易感类和恢复类。其中,易感类为车联网蠕虫可以感染的具有漏洞的车辆,感染类为被车联网蠕虫感染的车辆,恢复类为由于人为干预对于车联网蠕虫的查杀将感染类车辆转化为恢复类车辆。车联网中跟蠕虫传播相关的车辆只能处于感染类、易感类或者恢复类,易感类车辆可以被车联网蠕虫感染而转化为感染类车辆,感染类车辆可以被人为查杀蠕虫而转化为恢复类车辆。下面根据漏洞车辆服从泊松或者高斯分布来分别讨论车联网蠕虫的随机传播模型。 3.3.1 基于排队论的车联网蠕虫的传播模型 若如3.1节所述,车联网蠕虫在单位时间Δt内其感染车辆的数目服从泊松分布,即以均值λ感染车辆。若在单位时间Δt内,人们通过杀毒软件或者其他方式查杀车联网蠕虫的数目为μ,因此其符合排队论模型,那么其感染过程如下: 状态查杀的速度=感染的速率 λP0=μP1,n=0 (λ+μ)Pn=λPn-1+μPn+1,n≥1 根据平衡方程的结果,得到等式: 或者等价地: 于是:而且,一般地: 因此有: 若使该随机过程存在极限分布以及平稳分布的充分必要条件是上式中的分母有限,需要有: 因此,该模型存在极限分布以及平稳分布充要条件是λ<μ,即为了存在极限分布以及平稳分布,感染速率λ必须大于查杀速率μ;否则感染过程将不稳定或者导致传播灭绝。 3.3.2 基于马尔可夫链的车联网蠕虫的传播模型 由于车联网蠕虫在单位时间tn+1时刻的传播数目仅与tn时刻的传播数目有关,因此其符合马尔可夫链的传播条件,传播过程符合马尔可夫链。那么其在较小的时间Δt内,车联网蠕虫从状态n只能转移到状态n+1 或者n-1,或者保持不变。如3.1节所述,若车联网蠕虫感染主机的数目X~N(p×(r×300×i),(r×300×i)2σ2),那么其状态转移概率pjk为: 当j→j+1 时,其转移率为b(k,j)=Φ((k-(p×r×100×i))/(σ×r×100×i))-Φ((j-(r×100×i×p))/(r×100×i×σ));当j→j-1 时,其转移率为y(k,j)=rj;根据马尔可夫链的性质,那么当j→j时,其转移率为s(k,j)=1-rj-Φ((k-(r×100×i×p))/(r×100×i×σ))+Φ((j-(r×100×i×p))/(r×100×i×σ))。将其以矩阵的形式进行表示定义如下: 为了更加深入地验证并且分析车联网蠕虫的传播规律,编写了可以模拟车联网蠕虫传播的仿真器,仿真实验对于相同的实验内容进行1 000 次的重复操作,通过对于1 000次的实验结果进行平均得到相应模型的传播图像。图像的x轴表示感染主机数目,y轴表示单位时间,z轴表示感染的概率。下面对于实验结果进行相应的讨论。 图2 是关于车联网蠕虫Galton-Watson 分支过程模型的仿真结果。其中,图(a)为当车流服从泊松分布时,均值λ=0.8 时的仿真实验结果。从图中可以看到在蠕虫传播初期,蠕虫可以进行小规模的传播,但是随着传播的继续,网络蠕虫则走向灭绝。这也验证了定理2 的内容,即λ≤1 时,网络蠕虫必将灭绝。由于当车流服从正态分布且均值小于1 时实验结果类似,这里就不再赘述。图(b)为当车流服从泊松分布时,均值λ=2.0 时的仿真实验结果,由于没有网络蠕虫的查杀与防治,随着蠕虫感染时间的增加,网络蠕虫传播规模不断扩大的概率不断加大,最终可以感染全部漏洞主机。图(c)为当车流服从正态分布时,车流均值μ=5,σ2=25 时的仿真实验结果。与车流服从泊松分布的结果类似,随着蠕虫感染时间的增加,网络蠕虫传播规模不断扩大的概率也是不断加大,最终也可以感染全部漏洞主机。综上所述,无论车流服从泊松还是正态分布,由于没有人为干预车联网蠕虫的传播,当其均值大于1 时,车联网蠕虫最终可以感染全部漏洞主机的概率较大。 图3 是基于排队论的车联网蠕虫传播模型的仿真结果。其中,图(a)为当λ=μ时的仿真实验结果,从图中可以看到在蠕虫传播初期,其仅可以进行小规模的传播,但是随着传播的继续,车联网蠕虫最终会走向灭绝。当λ<μ时,实验结果结论相同,这里就不再赘述。这也验证了3.3.1小节的结论,当λ≤μ时,车联网蠕虫将走向灭绝的结论。图(b)、(c)、(d)为当λ分别为0.1、0.2和0.3,且μ为0.02时车联网蠕虫传播模型的仿真结果。从图中不难发现,在相同时间下,随着λ的不断增加,车联网蠕虫的传播区间也在不断扩大。例如,当单位时间为2 000 时,传播区间从[130,180]扩大到[500,600]。也就是说,车联网蠕虫感染更多车辆的概率将会变得更大。 Fig.3 Simulation results of worm propagation model in Internet of vehicles based on queuing theory图3 基于排队论的车联网蠕虫传播模型的仿真结果 Fig.4 Simulation results of worm propagation model in Internet of vehicles based on Markov chain图4 基于马尔可夫链的车联网蠕虫传播模型的仿真结果 图4 是基于马尔可夫链的车联网蠕虫传播模型的仿真结果。其中,图(a)、(b)分别为当车流均值μ=10、20 且方差σ=10 不变时仿真实验结果。从图中不难发现随着μ的不断增加,车联网蠕虫的传播区间也在不断扩大。例如,当时间为2 000单位时间时,传播区间从[28,38]扩大到[32,43]。图(c)、(d)分别为当方差σ=10、15 且车流均值μ=20 不变时仿真实验结果。从图中不难发现,在相同时间下,随着σ的不断增加,车联网蠕虫的传播区间跨度在不断扩大。例如,当单位时间为2 000 时,传播区间从[30,42]扩大到[30,50]。 本文提出了车联网蠕虫的随机传播模型。首先,在理想情况下,基于Galton-Watson分支过程对车联网蠕虫进行了建模;在现实情况下,当高速公路车流符合泊松分布时,基于排队论对车联网蠕虫进行了建模,并且研究了稳定性条件。当高速公路车流符合正态分布时,基于马尔可夫链对车联网蠕虫进行了建模。最后,通过仿真实验验证了提出的车联网蠕虫传播模型。



3.2 理想的车联网蠕虫随机传播模型




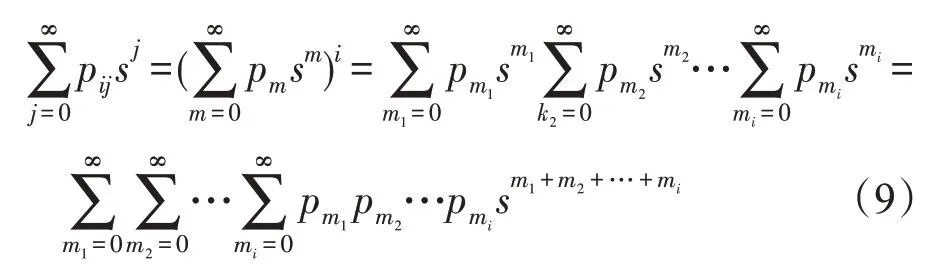





3.3 现实的车联网蠕虫随机传播模型


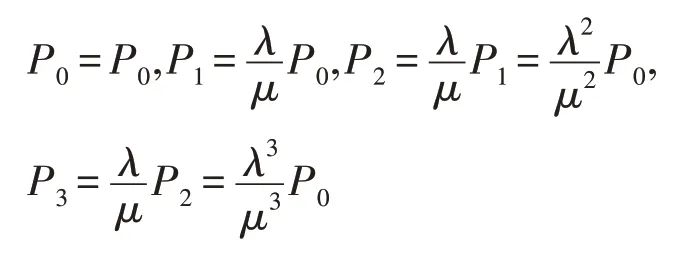




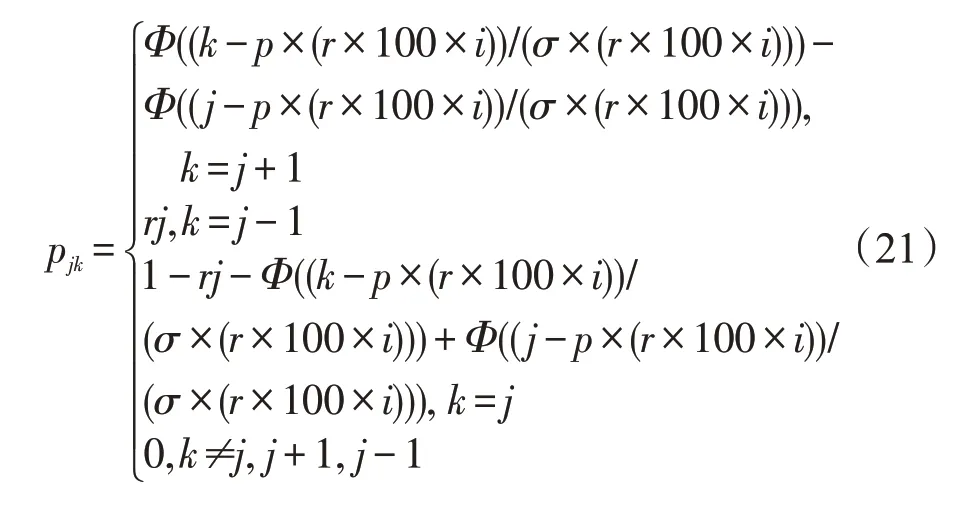

4 仿真验证及分析
4.1 车联网蠕虫的Galton-Watson 分支过程模型
4.2 基于排队论的车联网蠕虫的传播模型
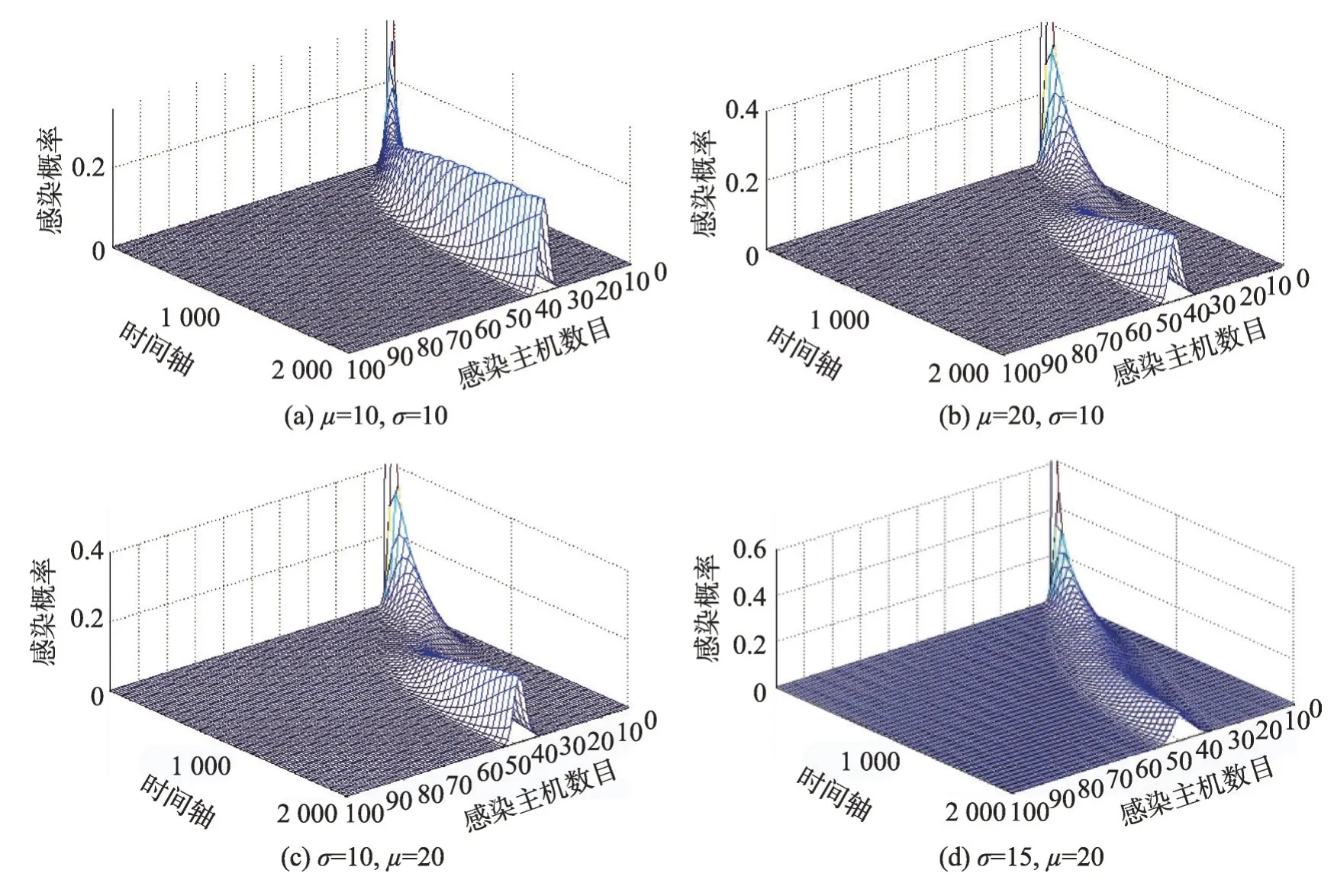
4.3 基于马尔可夫链的车联网蠕虫的传播模型
5 结论
