泊松分布样本均值与方差之差的渐近正态性

彭东海

（中山职业技术学院，中山 528404）

泊松分布是概率论与数理统计中一类重要的计数模型，由法国数学家Poisson[1]在研究二项分布当事件发生的概率p很小、试验次数n很大的情况下推导出的极限分布，常用于模拟单位时间或空间内稀有事件发生的总次数的分布模型，如单位时间内来到某公共设施要求给予服务的顾客数、机器出现故障的次数、保险公司收到的索赔次数等，它的定义如下：

定义1[2]：设随机变量X所有可能取值为0,1,2,…,而取各个值的概率为：

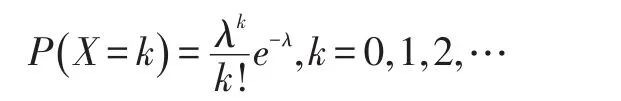
其中λ>0是常数，则称X服从参数为λ的泊松分布,记为X～P()λ。

泊松分布的一个重要性质是它的数学期望和方差都等于参数λ。称为等离散(equal dispersion)，因此实际问题中对计数资料能否选用泊松分布进行模拟的首要条件是看样本均值与方差是否近似相等，即需要进行过离散度（over dispersion）检验，最常用的过离散度检验由Böning提出的O统计量[3]的计算为：

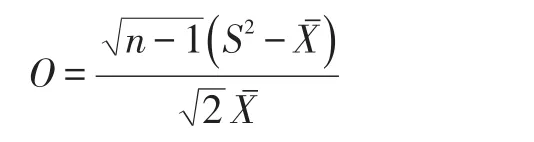
其中S2,分别表示泊松分布的样本方差与样本均值。文献[3]指出利用文献[4]的结果可得在总体为泊松分布条件下

有：

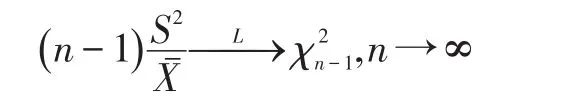
再利用卡方分布与正态分布的关系可得：

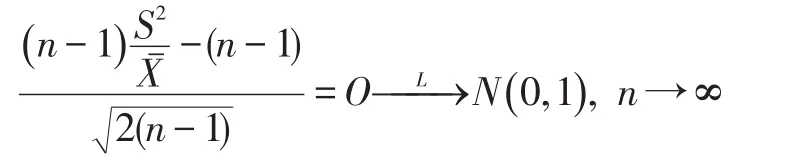
即O统计量具有渐近正态性。

下文，我们将利用多维向量的中心极限定理及delta方法给出在泊松分布条件下O统计量的渐近正态性的一种简便证明。

引理1[5]:记，设

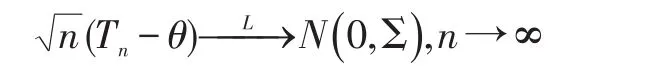
其中：

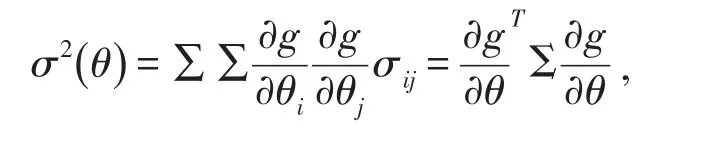
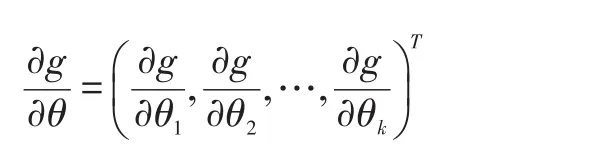
引理2：设随机变量X服从参数为λ的泊松分布，则X的前4阶原点矩分别为：

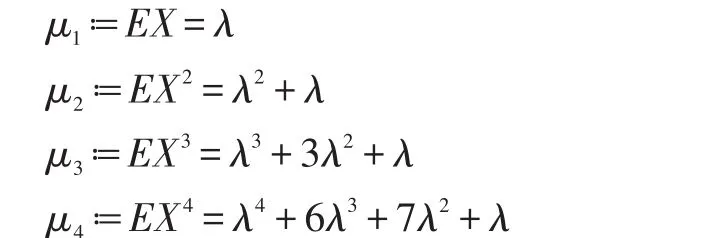
文献[6]给出了计算泊松分布的高阶矩的两个递推公式，此处，我们利用文献[7]中的定理3.6.8(Hwang)等式可得到一个新的递推公式。

证明：由[7]中定理3.6.8(Hwang)等式：

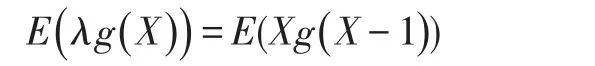
其 中 函 数 g(x)满 足, 且可知，若取，则有：

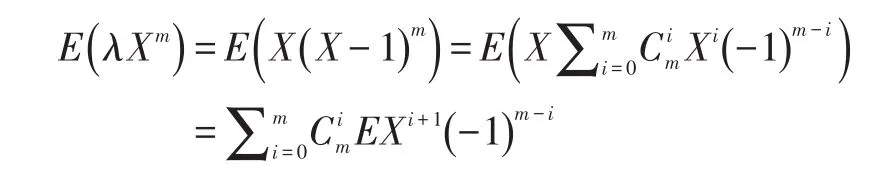
从而有：

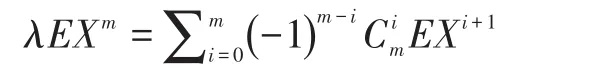
即：

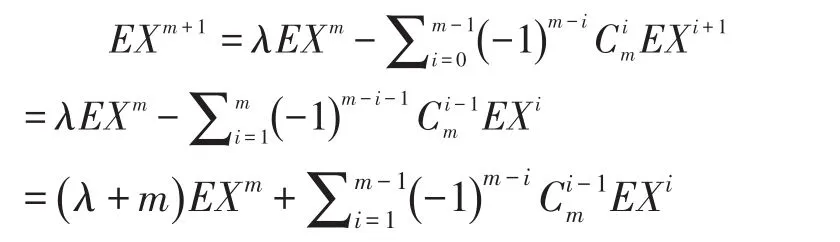
因此可得：

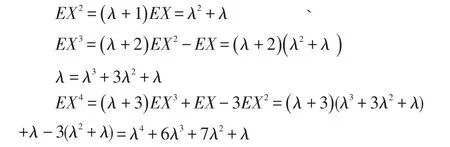
定理：从参数为λ的泊松分布总体中抽取容量为n的样本X1,X2,…,Xn,记：

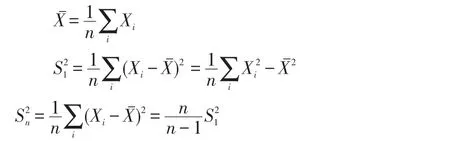
则有：

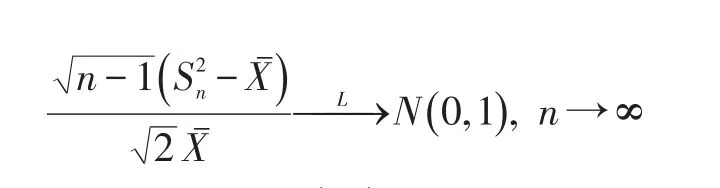
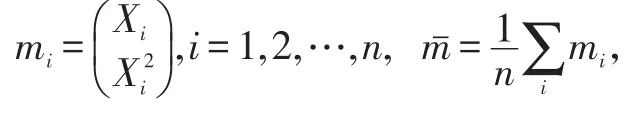
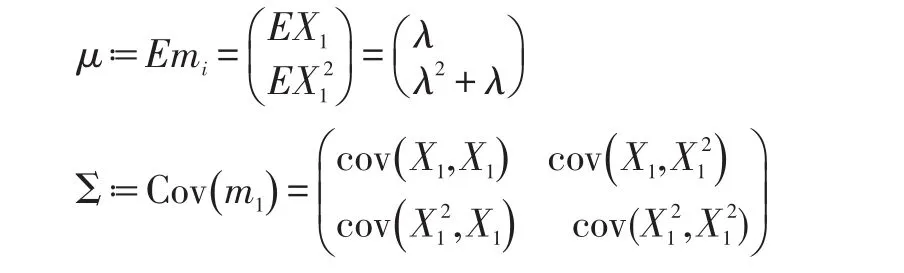
其中：

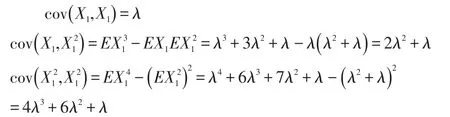
因此可得：

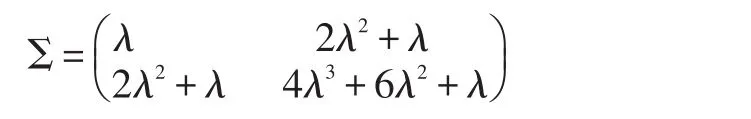
由多维随机向量的中心极限定理可知：

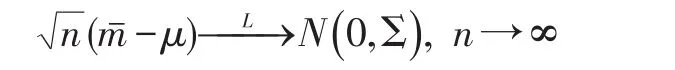
即：

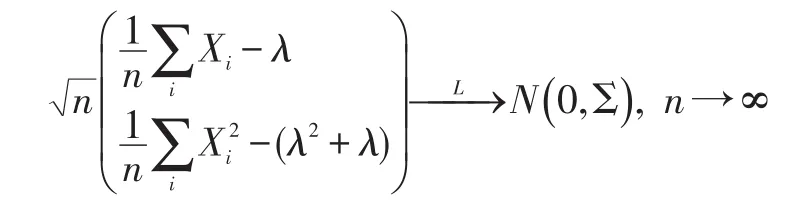
取则易知g关于t1,t2有连续的一阶偏导数，且：

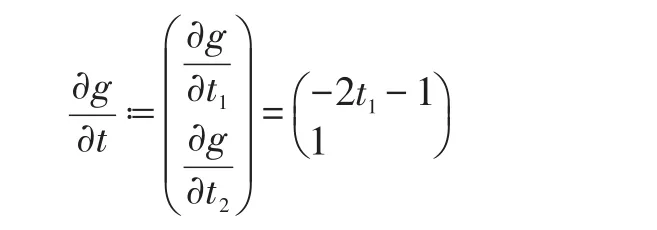
根据引理1有：

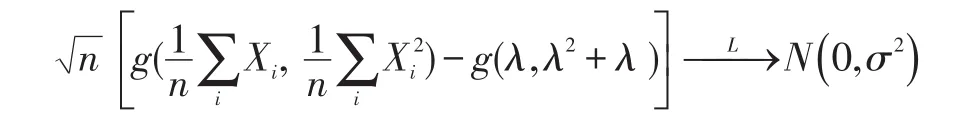
其中：

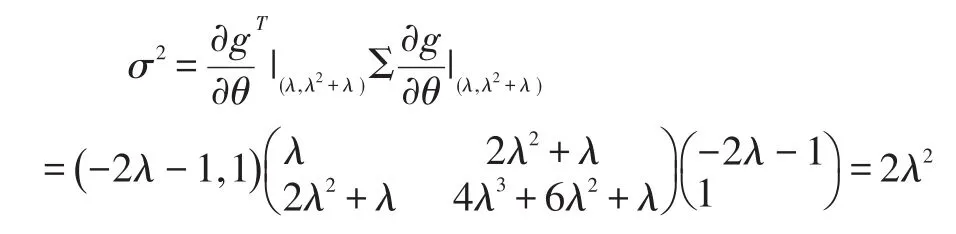
而：

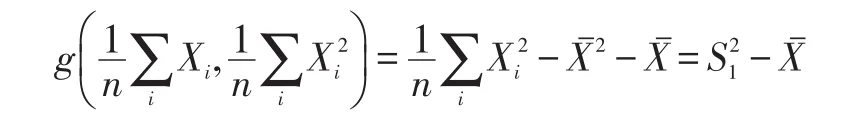
从而有：

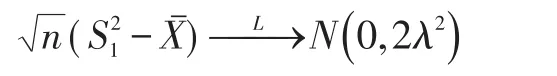
由于，因此由 Slutsky 公式可得：

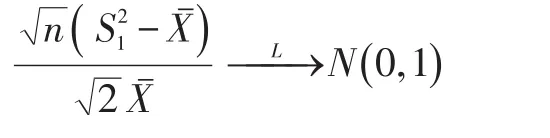
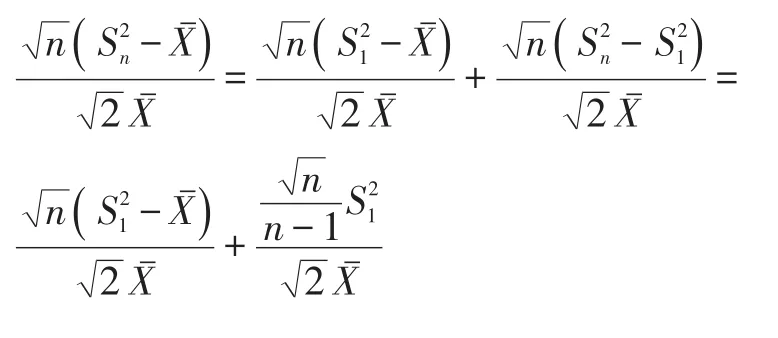
而，因此：

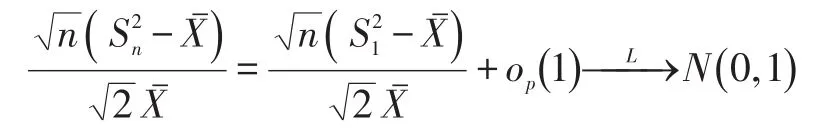
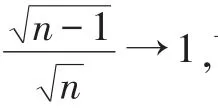
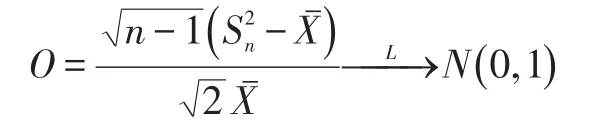
证毕。

参考文献：

[1]Cameron AC，Trivedi P.Regression Analysis of Count Data[M].Oxford University Press，1998.

[2]何远江，区景祺，尹小玲.概率统计引论[M].北京:高等教育出版社，2010：46-47.

[3]Böning D.A Note on Test for Poisson Overdispersion[J].Biometrika，1994(81):418-419.

[4]Hoel,P.G..On Indices of Dispersion[J].Ann.Math.Statist，1943(14):155-162.

[5]茆诗松,王静龙,濮晓龙.高等数理统计（第二版）[M].北京:高等教育出版社,1998：110-112.

[6]于晶贤，李金秋.泊松分布高阶原点矩的两种计算方法[J].数学的实践与认识，2010（11）：221-224.

[7]George Casella,Roger L.Berger.统计推断（英文版，原书第2版）[M].北京:机械工业出版社，2002：126-127.