建筑屋面雨水有压回补地下水理念与潜力评估

王兆庚，郭祺忠，2，练继建，陈 亮

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300354；2.罗格斯大学 土木与环境工程系，新泽西州，美国 08854）

1 研究背景

城市雨水回补地下水是雨水利用及资源化的一种重要形式，对于城市的发展具有重大意义。城镇化加快，不透水面积（硬化路面及建筑面积等）不断增加，改变了自然雨水水文过程［1］。据国家统计局、住建部公开数据，近40年内（1978—2017年），中国人口城镇化率增加了40.6%（由17.9%增长为58.5%），同时伴随着不透水面积的急剧增长，其中建筑与小区占城区面积的近70%［2］。该过程加大了地表径流，减少了雨水下渗量；使得近80%的降雨形成径流，雨水径流量增加70%左右，下渗量减少约40%，导致城市地下水无法得到补给、地表径流增加，引起城市水资源短缺及内涝频发问题［3-5］。《中国水旱灾害公报》［6］公开数据显示，近10年内（2008—2017年），北方平原区地下水含蓄量平均每年减少38 亿m3，逐步造成地下水空洞，且每年有近170 多个城市遭受不同程度的进水受淹或暴雨内涝，造成平均每年2000 亿元左右的经济损失。因此增加地下水含蓄量，减少城市内涝灾害的发生，迫在眉睫。然而，有关研究表明［7-9］，降落至地表的雨水，尤其是屋面雨水水质较好、污染较轻，较路面雨水具有更高的利用价值。而且降落至建筑屋面的雨水本身具有势能，这部分势能对于提高雨水利用效率，具有很高的开发价值。故加强雨水尤其是建筑屋面雨水的利用，以及屋面雨水资源化对于上述问题的缓解具有重大意义。

目前城市雨水利用方式有两大方面：雨水集蓄回用（二次回用、回补地下水等）［10］，以及人工滞留渗透技术（透水铺装［11］、生物滞留系统［12］、绿色屋顶［13］、植草沟［14］、下凹式绿地［15］、植物缓冲带［16］等）。此两方面中各项方式的侧重功能不同，但总体是以渗、滞、蓄、净、用为主，从而较大程度地发挥雨水的资源利用价值［17］。但针对上述两方面技术在增加地下水含蓄量方面，均存在空间利用矛盾的问题，其中人工滞留渗透技术（渗、滞）需布设相关措施，占据城市较大空间；雨水集蓄回用（蓄、净、用）需修建蓄水池，一个一般规模的蓄水池容积需200～400 m3/hm2［18-19］，同样涉及空间不足问题，与城市空间利用之间存在矛盾。而且，上述技术（除回补地下水外）原理基本为增大雨水滞留时间，使雨水自然下渗［20］，但这一过程时间周期长，对快速增加地下水含蓄量、有效缓解城市洪涝等问题，效果不明显。然而，现有的雨水回补地下水技术在快速增加地下水含蓄量方面具有优势［21］；不过这一途径仍存在不足：（1）目前的雨水回补地下水模式，均采用先集蓄、后净化、再回补的方式［17］，但在集蓄的过程中，使得降落到建筑屋面雨水的势能损失；且在集蓄中伴随长期蓄存易使雨水水质恶化，导致水中色度、浊度、COD、氨氮、细菌以及pH 值等多项指标超标［22-24］，引起雨水二次污染、更难净化的问题，增加了雨水的利用成本［25］；（2）雨水回补地下水的常用方法有地面入渗法和管井注入法两种［26-29］，但这两种方法具有不足之处。地面入渗法以自然入渗为主，时间周期长，且对场地（渗透性、占地面积）要求高；管井注入法，又可分为重力注入法、真空灌注法及加压灌注法。其中，加压灌注法为3 种方式中回补效率最高的一种，较无压自然回补，回补效率可提高15%～200%左右［30］，但加压回补需布设加压泵、储水罐等大型回补设备，且需要外界持续提供电能，使用成本高［31］。基于上述两方面问题增大了雨水的综合利用成本，因此应考虑开发一种将雨水收集、快速净化，并不需外界能量输入、直接回补地下水的模式，进而缓解上述问题。

对于城市而言，存在较多的建筑群（住宅建筑、商业建筑等），降落到建筑屋面上的雨水，其总量具有很高的可利用性，且建筑物屋顶雨水水质较好［32］。更为重要的，降落到建筑群屋面上的雨水具有高水头特点，该部分势能可用于提供回补所需压力，但这部能量很少被应用。因此在对建筑物屋面雨水进行简单、快速净化处理的基础上，利用该部分雨水具有的高压水头特点，实现建筑屋面雨水有压条件下回补地下水的雨水利用模式，对上述问题的解决具有重大意义。该项技术理念提出后，尚处于研究阶段，故本文基于上述内容以及国内外有压回补地下水的相关研究，以天津大学新校区为研究区，结合现有的加压回补数据建立计算模型，对建筑屋面雨水有压回补地下水的潜力进行评估，为该项技术的发展和推广提供参考。

2 建筑屋面雨水有压回补地下理念及计算模型

2.1 雨水利用潜力分析与计算雨水总量是指一个流域或封闭地区的降水总量，对于校园雨水集流面包括建筑屋顶、道路和绿地，该量的计算、评估方法目前多采用径流分析法［33］。针对本文中的研究对象所涉及的集流面为建筑屋面，故雨水总量的计算具体可阐述为：对特定研究区域、特定时间的雨水收集量的计算。其具体公式如下：

雨水总量计算式［34］为：

式中：W 为某区域内的雨水总量，m3；H 为某地区的降雨量，mm；A 为汇水面积，m2。

雨水可利用总量的计算公式［34-36］为：

式中：W′为某区域内的雨水可利用总量，m3；a 为径流系数；φ为有效雨量系数。

2.2 建筑物屋面雨水有压回补地下水理念及回补量计算建筑屋面雨水有压条件下回补地下水模式，如图1所示，在回补原理方面与目前加压回补地下水相同。其具体实施方式为：以建筑屋面为集流面，且建筑屋面兼具短暂储水功能，通过与屋面雨水收集、净化装置，雨水管，以及有压回补井相组合、连接，从而提升雨水回补时的水头压力，实现建筑屋面雨水有压回补地下水模式。由于没有成熟的回补理论指导，本文依据目前加压研究、相关回补试验结论，以及相关参数的定义，对建筑物屋面雨水有压回补计算参数进行等效、概化处理（具体阐述见本文3.3 章节），以此为基础，对该模式下的回补量进行评估计算。

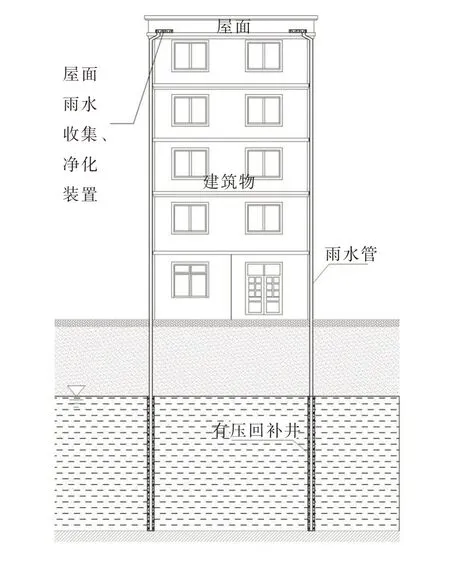
图1 建筑物屋面雨水有压回补地下水示意图

目前的回补地下水的理论研究仍处于探索阶段，还没有成熟的回补应用理论；而地下水抽取理论研究已相对成熟，故学者们将回补地下水看做抽水的逆过程［37］，将抽水理论应用到回补地下水中，在一定程度上解决了现有问题，但并不完全适用。降水井的影响半径可采用库萨金公式进行计算［38-39］，虽然可将回补看做降水的逆过程，但降水与回补过程中水的总“势能”不同，对同一场地，井内水位降低或升高相同高度时，抽水量远大于回补量，降水井影响半径也比回补井的影响半径大［30，37，40］。因此回补井的回补量不能完全按降水井的求解公式进行计算，需要对计算公式进行必要的修正。

2.2.1 现有理论公式 地下含水层回补量的裘布依公式［41-43］及影响半径的库萨金公式［38-39］：

式中：Q 为地下含水层回补量，m3/d；k 为潜水含水层渗透系数，m/d；hw为回灌后井水位到含水层底部距离，m；h0为潜水含水层饱和层的初始厚度，m；R 为影响半径，m；rw为回补井半径，m。

式中：sw为回灌后井内水位到含水层顶部距离，m。

2.2.2 推求适用于本模式的半经验公式 王会刚等［30］通过现场水泵加压回补试验研究，得出相关试验数据，该现场试验地点位于济南市城区，在地质与地理条件方面可代表北方平原、丘陵地区城市，与天津各方面条件十分接近；且试验中采用恒压回补地下水的方式，进行了0.05～0.20 MPa 的压力回补试验。该试验中所用压力与本文计算中所涉及的压力水头十分相近，故本文基于其所得试验数据，并结合本课题组针对该模式正在开展的试验研究，借用式（3）、式（4）的计算形式，采用更加适合于本模式计算评估的参数，推求出适用于建筑屋面雨水有压回补潜水含水层模式的回补影响半径及回补量的计算公式，并通过回归得出了系数。回补影响半径及回补量计算值与实测值的对比结果，见图2。

式中：R′为推求后的影响半径，m；he为建筑屋面距潜水含水层饱和层顶部距离（图3），m；k 为潜水含水层渗透系数，m/d；h0为潜水含水层饱和层的初始厚度，m。

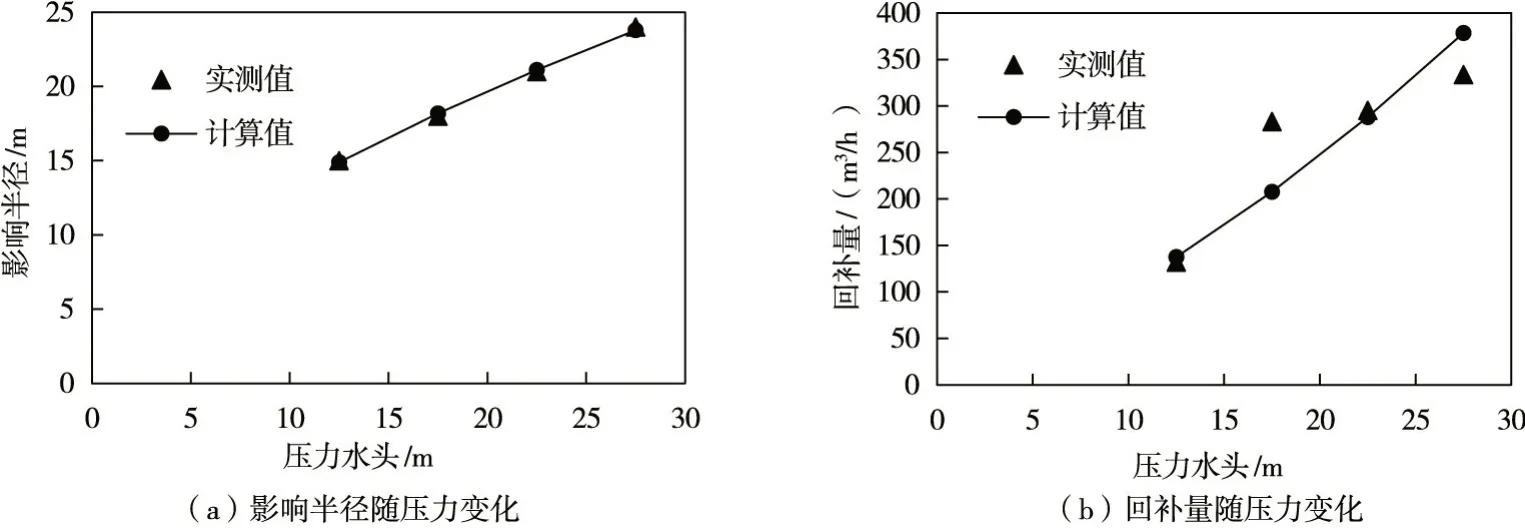
图2 推求后半经验公式计算值与实测值对比

式中：Q′为建筑屋面雨水有压回补地下水量，m3/h；k 为潜水含水层渗透系数，m/d；hi为屋面距潜水含水层底部距离（图3），m；h0为潜水含水层饱和层的初始厚度，m；R′为推求后的影响半径，m；rw为回补井半径，m。

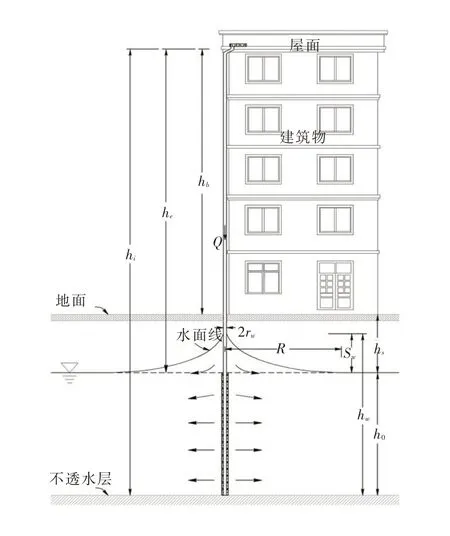
图3 建筑屋面雨水有压回补地下水回补量计算参数示意图

2.3 回补率计算本文中以回补率为衡量标准，对本文所述模式进行评估。该值为回补量与雨水可利用总量的比值，具体公式如下。

式中：rx为回补率，%；Q′建筑屋面雨水有压回补地下水量，m3/h；W′为某区域内的雨水可利用总量，m3/h。

3 实例研究——以天津大学新校区为例

3.1 研究区概况天津大学新校区位于天津市津南区大学城内，校园建设融合“海绵城市”建设理念，为天津市重点建设工程之一。校区占地总面积243.6 万m2，规划总建筑面积155 万m2，目前已完成一期90 万m2建设，其中建筑屋面总面积为217 699 m2，研究区建筑物高度为4.6～50.65 m，面积加权平均高度为17.45 m；图4为天津大学新校区所处地理位置及整体建筑分布概况。校园所属地区属半干旱大陆性季风气候，年平均降水量为522.2～663.4 mm；在年内分布上，6—9月降水量占全年降水总量的85%左右，且主要集中在7月下旬和8月上旬，占全年降雨总量的65%左右［44-45］。

图4 天津大学新校区建筑分布示意图

3.2 研究区屋面设计雨水可利用量计算

3.2.1 设计降雨强度计算 参照《天津市雨水径流量计算标准》DB/T29-236-2016 中天津暴雨分区下的第1 区设计暴雨强度公式（8），以及通过式（9）对平均暴雨强度q 进行单位转换，对研究区所属地区的1年一遇、5年一遇、10年一遇、25年一遇、50年一遇、100年一遇小时平均降雨强度Hx，y进行推求；计算过程中，降雨历时是一个十分重要的参数，在设计时该参数通常取为研究对象的汇水时间，该值的取值大小直接影响到小时平均降雨强度的计算结果；因本模式以建筑屋面为集流面，且建筑屋面兼具储水功能，故汇水时间也是本模式的一个重要控制参数；本文在综合考虑屋面集汇流时间、屋面最大可滞留雨水时间等因素前提下，将该参数分别假设为：5、10、30、60、120、1440及4320 min，以上述取值进行计算，分别得出不同重现期、不同降雨历时（雨水滞留时间）下的设计雨强；具体计算结果见表1。

式中：q 为平均暴雨强度，L/（s·hm2）；P 为设计重现期，a；t 为降雨历时，min。

式中：Hx,y为变换单位后的平均暴雨强度，mm/h；q 为平均暴雨强度，L/（s·hm2）。

3.2.2 不同重现期、不同降雨历时（汇水时间）下的屋面雨水可利用总量计算 不同重现期下的校园屋面雨水可利用总量的计算以重现期为1年一遇、降雨历时（雨水滞留时间）为5 min 为例，其他假设情况的计算结果见表1。通过雨水可利用潜力的计算公式（1）—（2），结合式（8）—（9）所得降雨强度，

计算出重现期为1年，降雨历时（雨水滞留时间）为5 min 的屋面雨水可利用总量W ′1,5min。

表1 研究区不同设计重现期、屋面不同汇水时间下的有压回补参数

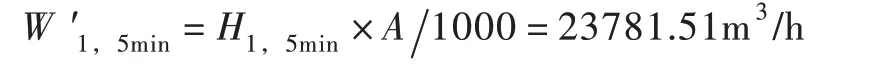
上述计算中：W ′1，5min为1年一遇、5 min 降雨历时（雨水滞留时间）下的校园内屋面雨水可利用总量，m3/h；H1，5min为研究区所属区域1年一遇、5 min 降雨历时（雨水滞留时间）下的降雨强度，mm/h；A为汇水面积，m2，校园建筑物屋面汇水总面积为：217 699 m2；a 为径流系数，φ为有效雨量系数。因本研究涉及的集流面为屋面，其径流系数取值范围一般为0.9～1，其取值对屋面雨水可利用总量影响很小，且本模式中雨水是滞留于屋面，不存在弃流状况，因此基于上述两方面原因将两参数均取为1。

3.3 研究区建筑屋面雨水有压回补地下水总量计算据相关研究［46-47］及地质勘查报告，天津地下含水层由于渗透系数较小的黏土弱透水层阻隔，在约100 m 勘察深度范围内主要形成一个潜水层与4 个承压含水层，潜水含水层主要由粉土组成。潜水层大致分布于地面至标高-10 m 范围内，初始水位埋深（hs）约2 m，潜水含水层厚度（ho）约为8 m。且相关地质勘查报告显示，研究区域潜水层渗透系数（k）为0.2 m/d。

对于研究区建筑屋面雨水有压回补地下水总量的计算，具体步骤如下：①确定不同建筑回补系统数目m。回补系统的数目直接关系到回补总量的大小，本文所研究的回补模式中对于回补系统的布置，是在建筑雨水管布置的基础上进行的，首先参照《屋面工程技术规范》GB 50345-2012 相关要求，将每个雨水管的屋面辐射汇流面积确定为150 m2，依据不同建筑的屋面面积确定雨水管数目，后将每个雨水管与有压回补井对接，即得到回补系统的布设数目；②计算单个回补系统回补能力Q′。以高度为控制因素，通过上述式（5）—（6）计算单个回补系统的回补能力；③计算单元建筑屋面雨水回补量Q′j。以单个建筑屋面为单元，该单元回补能力为该单元建筑高度下对应的全部回补系统的回补能力总和Q′i，如式（10）所示；并采用式（1）—（2）计算单元建筑屋面所对应的雨水可利用量，然后与单元建筑屋面雨水回补能力进行对比，从二者中选取最小值（当单元建筑屋面雨水可利用量大于单元建筑屋面雨水回补能力时，取单元建筑屋面雨水回补能力，将多余雨水做弃流处理；当单元建筑屋面雨水可利用量小于单元建筑屋面雨水回补能力时，取单元建筑屋面雨水可利用量；如式（11）所示），即为该单元建筑屋面所对应的的雨水回补量；④计算研究区不同高度建筑屋面雨水有压回补地下水总量Qt。对③中所得单元建筑屋面对应的回补量进行求和，如式（12）所示，即可得研究区内不同高度建筑屋面雨水有压回补地下水的总量，具体计算结果见表1。

式中：Q′i为单元建筑屋面雨水回补能力，m3/h；m 为不同建筑回补系统数目，个；Q′为单个回补系统回补能力，m3/h。

式中：Q′j为单元建筑屋面雨水回补量，m3/h；Q′i为单元建筑屋面雨水回补能力，m3/h；W′(x,y)-i为单元建筑屋面所对应的雨水可利用量，m3/h。

式中：Qt为不同高度建筑屋面雨水有压回补地下水总量，m3/h；Q′j为单元建筑屋面雨水回补量，m3/h。

3.4 回补效果评估

3.4.1 有压回补率计算 利用式（7），并结合上述计算结果，可对研究区在该模式下的回补率进行计算。

式中：rx为回补率，%；Qt为不同高度建筑屋面雨水有压回补地下水总量，m3/h；W ′x，y为不同重现期、不同降雨历时（汇水时间）下的屋面雨水可利用总量，m3/h。具体计算结果见表1。

3.4.2 无压回补计算 无压回补地下水即雨水降落至地面后自然下渗至地下水的过程。在相同降雨强度、同样假设雨水降落至地面后可在地面滞留一定时间的情况下，无压回补量主要与渗透面积、土壤渗透系数及降雨历时（雨水滞留时间）有关，且在降雨历时（雨水滞留时间）、土壤渗透系数一定的情况下，无压回补量与渗透面积成正比。若假定无压回补在相同的滞留时间下与有压回补具有相同的回补率，即无压回补总量与有压回补总量相同，则可通过式（14）计算无压回补所需渗透面积，从而对无压回补进行粗略评估。

式中：Aw为无压回补所需渗透面积，m2；Qw为无压回补总量，m3/h；k 为土壤渗透系数，m/d；t 为降雨历时，min。

如表2所示，在降雨历时（雨水滞留时间）同样取为24 h 的情形下，无压回补要达到有压回补的相同的效果，需要提供上表中所示的渗透面积来消纳屋面排下的雨水，而现实中对于城市建设而言，无法为该种回补方式直接配置如此大的地面渗透面积（60% ～130%的屋顶面积，即表2地面渗透面积占217 699 m2建筑屋面总面积的比例）；无压回补方式将会占据城市较大空间，与城市土地利用存在矛盾；而在此方面，屋面雨水有压回补方式相对无压回补更加具有应用优势和推广价值。

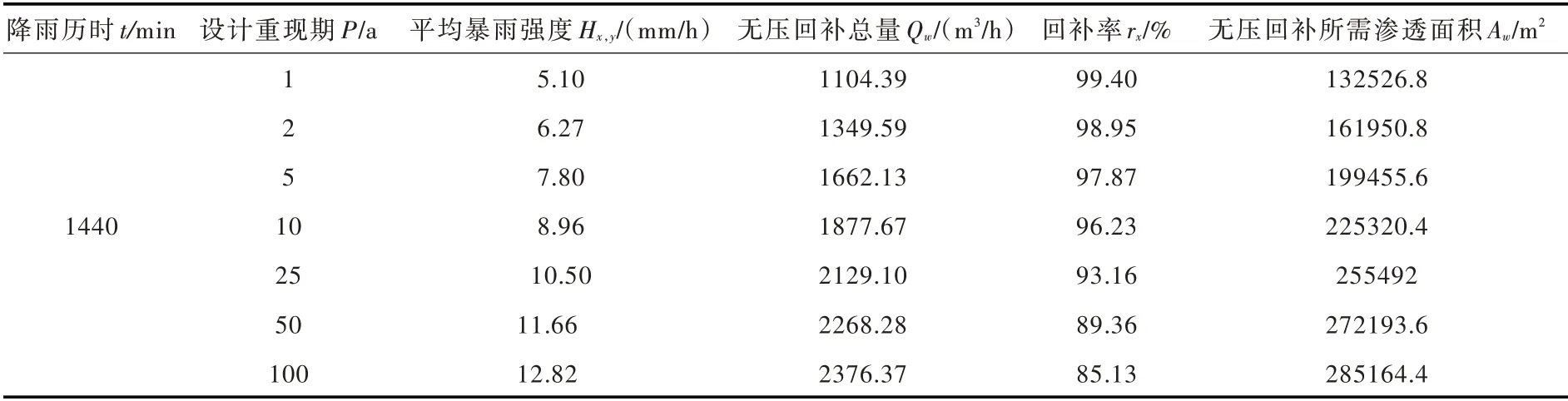
表2 无压回补计算

3.4.3 回补效果分析 通过表1中数据以及图5，对研究区不同设计重现期、屋面不同汇水时间下的回补情况进行对比分析；在本文所述研究模式下，降雨历时（雨水滞留时间）、降雨重现期是影响回补率的两个最为重要的参数；通过表中数据以及图中趋势显示：①回补率与降雨重现期呈负相关关系，即回补率随降雨重现期的增加而呈减小趋势，具体阐述为，在建筑屋面高度、数量一定的前提下，研究区域内的回补总量为定值，若单位时间降雨量越大，则回补率越小，弃流量越多。②回补率与降雨历时（雨水滞留时间）呈正相关关系，即回补率随降雨历时（雨水滞留时间）的增加呈增加趋势，具体描述为，对于一场降雨，建筑屋面可滞留或储存雨水的时间越长，可为本回补模式提供越长的回补时间，则回补率越高；反映到工程实际中，体现为可通过相应工程措施，延长建筑屋面的汇水时间而增大该模式下的回补率；如本文中计算显示，若建筑屋面可将雨水滞留或储存24 h，则在本模式下，对于25年一遇以内降雨可实现将90%以上降雨回补至地下水，对于50年一遇和100年一遇降雨回补率也可达85%以上。上述计算结果表明本文所提回补模式，其回补利用量十分可观。对于需要外排的雨水在屋面设置溢流口，将其从屋面排出，排至城市管网或另行收集，可用于其他方面。

故由以上分析可得，建筑物屋面雨水有压回补地下水这一雨水利用模式，具有较强的适用性和应用价值，一方面基本解决雨水收集后难以储存的问题，可增加地下水含蓄量；另一方面，可短时、有效减少地表径流量，有效缓解城市内涝灾害。

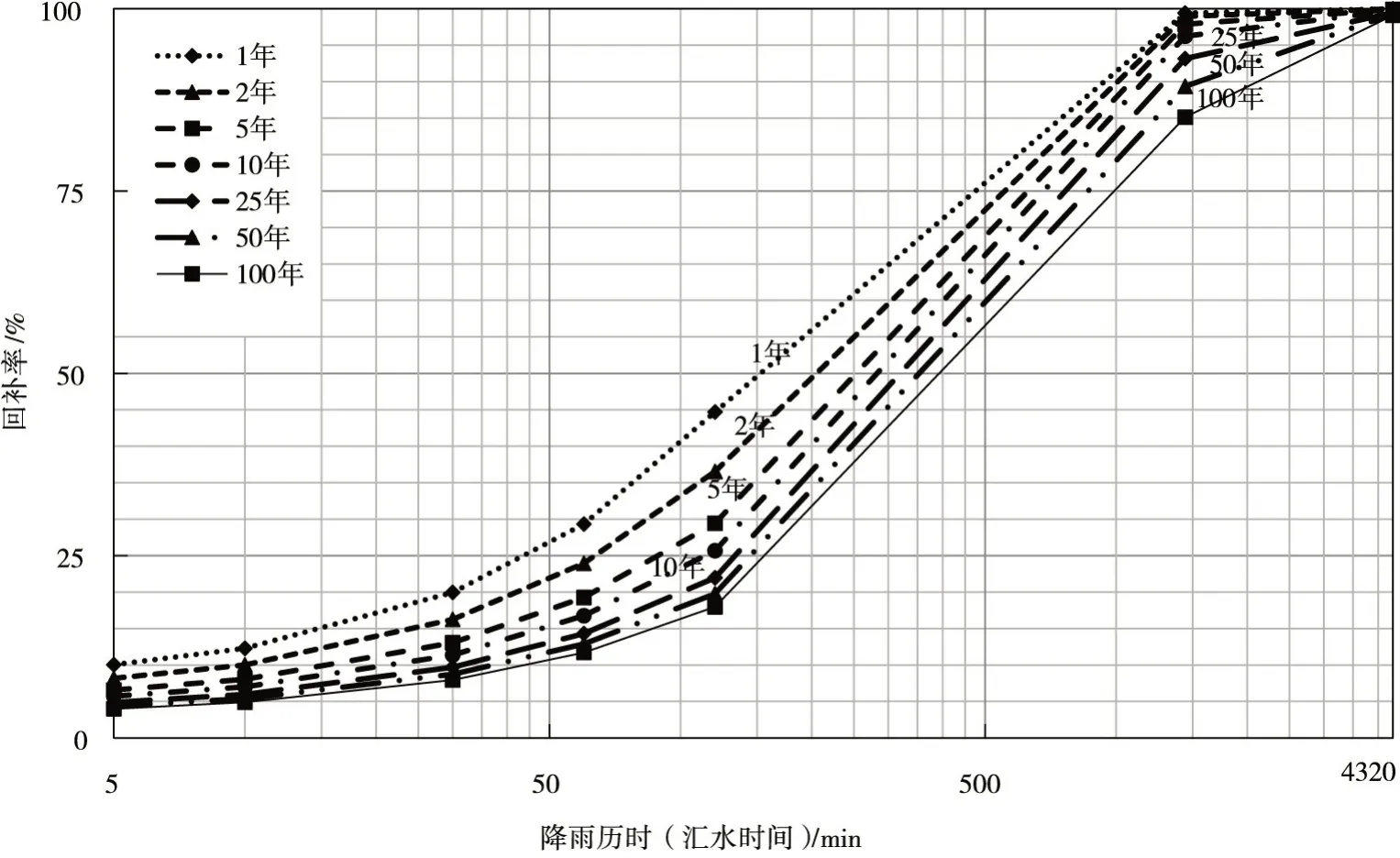
图5 研究区建筑屋面有压回补地下水回补率～降雨重现期～降雨历时（建筑屋面雨水滞留时间）相关关系

4 结论

本文提出了建筑物屋面雨水有压回补地下水理念，通过水泵加压回补地下水的现场实验数据推导出了半经验公式，并以天津大学新校区为研究区，选取与实地状况基本相符的土壤渗透系数等相关参数，对该模式进行相关计算与潜力评估。利用天津市暴雨公式计算了假设的不同降雨重现年及历时的设计雨强，并以此为基础，计算出本模式应用于研究区中不同设计情况下的回补率。计算结果表明，本模式的回补率与降雨历时（建筑屋面汇水或滞留时间）有直接关系，对于一场降雨，建筑屋面可滞留或储存雨水的时间越长，则回补时间越长，相应回补率越高。反映到具体的工程实践中，可通过相应工程措施，延长建筑屋面的汇水、储水时间而增大本模式的回补率。如本文中计算显示，对降雨历时（建筑屋面可将雨水滞留或储存时间）假设为24 h 情形下，25年一遇以内降雨可实现将90%以上降雨回补至地下水，对于50年一遇和100年一遇降雨回补率也可达85%以上。

通过本文的计算评估，建筑物屋面雨水有压回补地下水这一创新型雨水利用模式，是对雨水回补地下水方法的一种提高和拓展。对于本模式正在进一步研究中，其应用效果仍在深入探索与验证。在对建筑物屋面雨水进行处理至水质达标的前提下，充分利用了建筑物屋面雨水所具有的水头压力，从而在不借助外界措施和能量、不占据多余空间的前提下，形成屋面雨水有压回补地下水模式，进而提高雨水回补效率。该模式具有较高的推广性和应用价值，可节约城市雨水利用空间及成本，并对增加城市水资源利用量及减轻城市内涝灾害具有重大意义。