大型弧底梯形渠道“适缝”防冻胀机理及应用研究

江浩源，王正中，2，王 羿，刘铨鸿，葛建锐

（1.西北农林科技大学 旱区寒区水工程安全研究中心 旱区农业水土工程教育部重点实验室，陕西 杨凌 712100；2.中国科学院 寒区旱区环境与工程研究所冻土工程国家重点实验室，甘肃 兰州 730000）

1 研究背景

随着西部大开发战略的持续推进，西部水资源短缺问题将成为制约旱寒区经济社会发展的瓶颈。我国南北水资源分布极不均衡，为了适应我国经济社会科学持续发展，优化水资源配置，长距离调水工程得到快速发展［1］，衬砌渠道因其造价低、输水效率高、易于施工、便于管理等优点，一直是长距离引调水工程的主要输水形式。但对于我国西部旱寒区而言，冬季漫长且气温低，渠道工程冻胀破坏普遍严重［2-4］，表现出鼓胀和隆起，严重时发生翘起、架空或失稳滑塌等破坏形式，影响渠道功能的发挥。因此，对于西部旱寒区而言，采取何种措施来有效“回避、适应、削减或消除冻胀”是引调水渠道工程建设的关键。

目前，旱寒区渠道工程主要依据自身所处环境，从“温、水、土”等方面采取因地制宜的防冻胀措施，如采用低导热系数保温板［5］、高热容相变保温衬砌［6］等措施来减少渠基土热量散失；采用上部土工膜防渗［7］，下部卵石、碎石或化学改性土进行渠基换填［8］等措施，以减少渗漏及水分迁移量。理论及实测研究表明［9-13］：沿渠道周边冻胀过大及突变是渠道冻胀破坏的主要原因，可采用宽浅式缓边坡、弧形坡脚或弧形渠底；同时，可结合柔性纵向伸缩缝（简称纵缝）来减少约束，适应变形，改善衬砌板受力，削减冻胀。其中，纵缝的合理布设对冻胀破坏影响非常显著。

《水工建筑物抗冰冻设计规范》［14］（下称“《规范》”）建议寒区衬砌渠道应适当增设纵缝，但其布设形式多依据工程经验来确定，没有具体的科学依据。目前，王正中、刘旭东等［9-10］对纵缝位置进行了探索，认为预先在裂缝位置处设置纵缝，可达到削减渠道冻胀破坏的目的。他们采用ADINA 有限元软件对纵缝防冻胀效果进行计算，认为纵缝的存在可使衬砌板与渠基冻土变形协调，削减衬砌板的冻胀不均匀性及其最大冻胀力，从而达到减轻渠道冻胀破坏的目的。

然而，以上研究仍存在以下不足。（1）将渠基冻土简化为“冷胀热缩”材料，基土冻胀仅采用热力耦合模型，未能综合考虑水分迁移、冻结相变及横观各向同性冻胀等作用的水-热-力三场动态耦合冻胀作用，使计算误差偏大；（2）采用衬砌-基土间法向、切向冻胀力及冻胀变形量来间接评价衬砌板受力状态的改善，未能真实反映出衬砌板自身的应力分布和破坏情况，无法准确分析出纵缝削减渠道冻胀受力的效果；（3）纵缝的位置、宽度、个数及其组合与削减冻胀效果之间的关系未得到精确量化，包括适应基土冻胀变形的合适的纵缝位置、合适的纵缝宽度、合适的纵缝个数及其组合，即“适逢”，亟待将“适变断面”的概念［9-10］提升到“恰当适变而不过度适变”的精准程度。

针对上述问题，基于水-热-力三场耦合理论，采用多物理场仿真软件Comsol Multiphysics 建立了考虑水分迁移、相变潜热及横观各向同性冻胀特征的渠基土三场耦合冻胀模型，考虑纵缝填充的接触本构及衬砌-基土相互作用，建立了寒区渠道设纵缝防冻胀分析模型；并结合旱寒区长距离调水工程中广泛应用的水力特性优越、抗冻胀优良、水面蒸发小的大型窄深式弧底梯形渠道冻胀受力变形特点，以衬砌板正应力分布均匀度为一级指标，以强度为二级指标，对大型渠道“适缝”防冻胀机理进行探讨，对纵缝位置、宽度、个数及其组合进行优化分析，提出合理的纵缝布设形式，以期为衬砌渠道“适缝”防冻胀措施的深入研究提供科学依据，对旱寒区渠道工程建设具有重要意义。

2 设纵缝衬砌渠道冻胀分析模型

我国季节性冻土区冬季气温低且持续时间长，在科学计算渠基土水-热-力三场耦合冻胀变形［12-13，15-16］前提下，考虑衬砌-基土的相互作用及纵缝填充的变形特点，提出了相应的接触本构模型。将渠基冻土-衬砌结构-接缝整体作为一个系统，建立了设纵缝寒区渠道冻胀分析模型。

2.1 渠基土水-热-力三场耦合冻胀模型渠道沿渠长方向长度远大于其垂直于渠长方向长度，可将衬砌渠道冻胀问题按平面应变问题进行处理，采用x-y 平面的笛卡尔坐标进行描述。

2.1.1 渠基土水热耦合控制方程 因土颗粒间隙较小，可忽略热对流及热辐射，根据傅里叶传热定律及热量守恒方程，可求得非稳态热传导平衡方程：

式中：T 为温度，℃； ρ 和ρi分别为土体和冰密度，kg/m3；Cp为考虑原位水相变潜热的土体等效定压热容，J/（kg·℃）； λeq为土体等效导热系数，W/（m·℃）； Lf为冰水相变潜热，取值为333 kJ/kg；θi为迁移水冻结成冰量。

主要考虑土颗粒、水及冰相［13］，对上式等效系数进行展开，得：

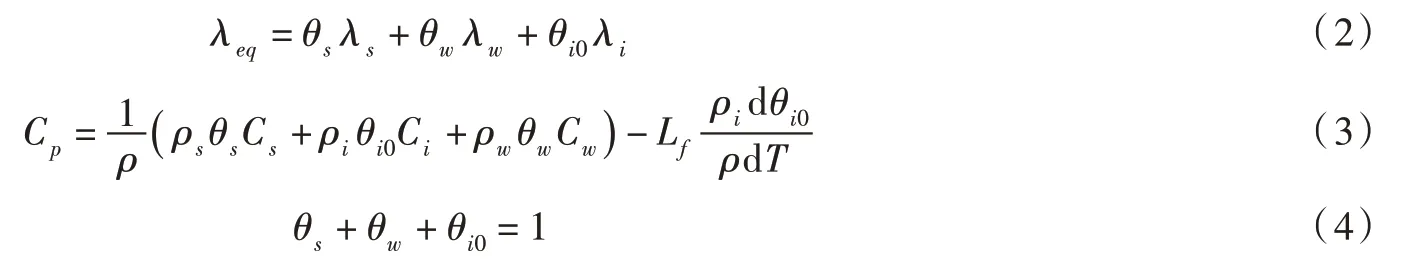
式中： θs、 θw、 θi0分别为土颗粒、初始含水量及原位冰含量； λs、 λw、 λi分别为土颗粒、水及冰相导热系数；Cs、Cw、Ci分别为土颗粒、水及冰相的定压热容。

多孔介质水分迁移遵从达西定律，单元内满足质量守恒方程，则水分场基本微分方程［12，17］如下：

式中： k 为土体渗透系数，m/s； k0为未冻土渗透系数，m/s；T0为土壤水冻结温度，℃； sep 为冰透镜体位置，m； β 为试验参数。

土壤冻结区冰颗粒周围存在少量未冻水膜［18］，其水分迁移驱动力可根据Clapeyron 方程推导为温度梯度的函数［19-21］，则水迁移至冻结面处冻结成冰所产生的热量方程［13，15］如下：

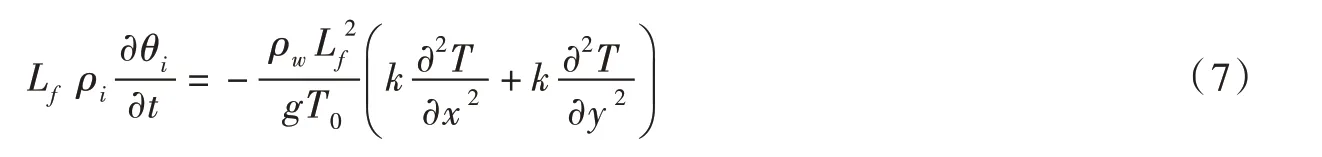
2.1.2 土体冻胀本构 研究表明［16，22］，冻土在沿温度梯度方向上冻胀变形值最大，而垂直于温度梯度方向很小，且二者冻胀量的比值随土质、含水量和冻结速率的不同而变化，目前尚处于探索阶段。基于上述原因，暂且只关注沿温度梯度方向的主冻胀，平面应变控制方程如下所示。

平衡微分方程：

物理方程：

几何方程：

结合冻胀率求解方程，对初始应变值进行坐标转换，方程［12-13］如下：

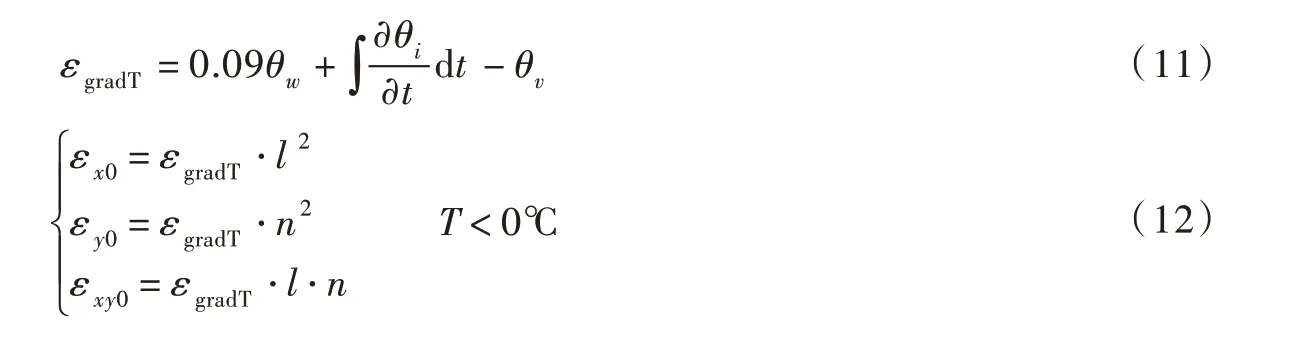
式中： εgradT为沿温度梯度方向的原位水及迁移水冻胀体积变化率；θv为土体孔隙率； l 、 n 分别为温度梯度向量的方向余弦。

联立式（1）、式（7）、式（8）、式（11）构成渠基冻土的水分场、温度场、变形场的三场耦合控制方程。目前，冻土水-热-力耦合模型得到较快发展，如白清波等［23］引入“固液比”概念，得到了冰含量和土体负温、未冻水含量之间的经验关系，建立了水热全耦合模型；Liu 等［24］引入土水特征曲线和Clapeyron 方程及力学本构，建立了水-热-力三场耦合的理论框架；Li 等［25］基于该理论框架，以冻结曲线作为联系方程，基于渠道离心模型对模型进行了验证。这些模型都在不同方面完善了冻土水-热-力三场耦合模型。而本文模型是在借鉴这些模型反映冻土水分迁移和相变潜热特征的基础上，侧重考虑冻土的横观各向同性冻胀特征，即冻土沿温度梯度方向为主冻胀方向，以求得到更合理的冻胀力分布规律。

基于文中模型，刘月等［15］以某一输水支渠为例，计算的冻深及衬砌板变形结果接近于实际情况；王正中等［12］分析了不同尺寸衬砌渠道的冻胀变形及应力分布，计算得到的衬砌破坏位置与现场一致；王羿等［13］基于分层优化理论，提出了“水力+抗冻胀”双优断面设计理念；Liu 等［16］引入横观各向同性冻土本构，并采用室内、现场试验对模型进行了验证。因此文中的三场耦合模型可满足工程要求。

2.2 考虑渠基冻土-衬砌相互作用的接触模型

2.2.1 模型提出 衬砌-基土间冻胀力大于二者冻结强度时，将会产生脱离或滑动。目前，对于现浇混凝土衬砌板与渠基冻土界面多采用满足摩尔-库伦准则的接触单元模拟，但其对于法向冻结力的模拟及其计算收敛性较差，不符合界面间实际受力情况且计算成本较高。基于此，拟采用弹性薄层单元，对其进行修正，以模拟上述行为。

弹性薄层单元的实质是在结构间的接触界面处建立具有一定刚度的法向和切向弹簧单元，其弹簧刚度可随弹簧的拉伸量非线性变化。依据结构之间的相对位移来计算二者之间的接触反力，并根据反力来进一步调整二者之间的相对位移，基本方程如下：

式中： σn、 σt分别为法向和切向弹性薄层反力，MPa； kAn、 kAt分别为薄层单元法向和切向刚度MPa/m； unl、 utl分别为衬砌法向和切向位移，m； uns、 uts分别为土体法向和切向位移，m。结合衬砌-基土相互作用情况，对上述方程的法向和切向刚度进行修正。

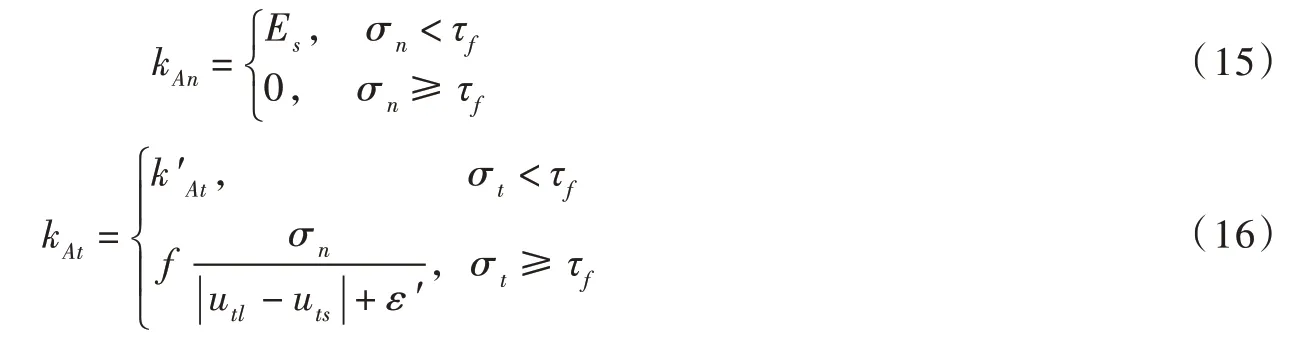
式中： Es为基土弹性模量，MPa；τf为基土与衬砌的冻结强度，MPa； k′At为基土-衬砌间未达到冻结强度时的剪切刚度，MPa/m； f 为基土-衬砌摩擦系数； ε′为大于0 的极小数。

2.2.2 模型验证 基于文献［26］，选取试验温度-5 ℃，含水率13.1%，法向压力为100 kPa 和200 kPa的两组冻土-混凝土界面剪切试验数据，采用上述接触模型对直剪试验进行数值模拟，以验证接触模型的合理性。由试验数据近似得： k′At=320 MPa/m，f =0.8，τf分别取0.20 和0.25 MPa，次峰值强度对应剪切位移取2 mm。有限元模型及结果对比如图1所示，数值模拟结果与试验结果基本一致，且可反映出冰胶结作用对界面强度的影响，因此该模型可合理反映出冻土-混凝土衬砌间的接触行为。

2.3 纵缝填充接触模型渠道工程常在衬砌板上设置纵缝，以适应渠基土变形，减少破坏。纵缝内部宜填充黏结力强、变形性能大、耐老化的柔性材料，如沥青砂浆、焦油塑料胶泥等，而聚氨酯砂浆因施工方便、适应变形能力强、对寒区气候适应性好等特点而被广泛使用。选取新疆某供水工程中采用的纵缝进行模型建立，如图2所示，缝内填充聚乙烯闭孔泡沫板，并采用聚氨酯砂浆灌缝止水。

图1 有限元模型及结果对比图

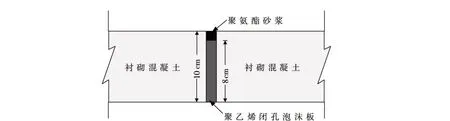
图2 渠道纵缝布置示意

渠道冻胀变形过程中纵缝主要发生挤压和分离等行为：纵缝两侧的衬砌板和底部的基土对纵缝变形形成强约束作用，在衬砌板挤压纵缝时，其挤压刚度先基本不变，在达到其极限挤压变形时，等同于纵缝闭合的状态，此时相当于衬砌板直接接触；衬砌板在基土冻胀产生弯曲张拉时，在拉伸应变达到纵缝填充-衬砌板黏结强度下的极限拉应变时，纵缝将会产生分离，其变形行为与面板坝中的面板间竖缝基本一致，因此可借鉴面板竖缝的模拟方法［27-29］，以反映渠道衬砌板间纵缝的变形特点。纵缝宽度约为1 ～4 cm，采用无厚度弹性薄层单元可避免纵缝宽度过小而无法进行网格划分的问题，并可较好地将面板间竖缝的模拟方法应用到渠道衬砌板间纵缝模拟，其理论方程如式（13）、式（14）所示。通过对法向刚度进行修正，从而提出纵缝填充接触模型。

式中： Ejt、 Ejc、 Ec分别为纵缝法向张拉、挤压和混凝土模量，MPa； εt、 εc分别为纵缝极限张拉、挤压应变值；unl、uns分别表示纵缝上、下侧衬砌板法向位移值，m； b 为纵缝宽度，m。

面板坝中的面板间竖缝计算模型已较为成熟，如孔宪京等［27］针对高面板坝，提出减少竖缝填料刚度及增加竖缝宽度等方法来减少面板高应力区；周墨臻、张丙印等［28-29］指出设置软缝可有效降低面板的坝轴向挤压应力。上述学者的计算结果均得到了工程实践的验证，且提出的宽软缝措施已应用于面板坝工程。而渠道纵缝模型正是基于面板间竖缝模型建立的，因此该模型可满足工程要求。

2.4 “适缝”削减冻胀效果评价指标混凝土衬砌属于薄板壳结构，全断面正应力分布特征可反映其适应基土冻胀变形的能力［4］。而极差是评价一组数据离散度最简单的方法，可用来衡量衬砌正应力分布的不均匀性，极差越小，表示数据的离散程度越小，即自身受力越均匀［30］。基于此，引入正应力分布均匀度指标，即未设缝与设缝后的衬砌板正应力极差之差值，除以未设缝的正应力极差进行归一化处理，如式（18）所示。

式中： S 为正应力分布均匀度； Rσ_未设缝、 Rσ_设缝分别为未设缝和设缝后衬砌板的正应力极差。

该指标既可表示衬砌板受力均匀化的程度，亦可反映出衬砌板削减冻胀的程度。该值越大，表示衬砌板受力越均匀，应力状态改善越明显，削减冻胀效果越好。然而该指标无法界定衬砌板是否发生破坏，故引入强度指标。综上，选取衬砌板上下表面沿渠周长正应力分布均匀度为一级评价指标，以强度为二级评价指标，可合理准确地评价“适缝”防冻胀效果。

3 有限元模型及参数选取

以新疆某供水工程大型弧底梯形渠道为工程背景，采用多物理场仿真软件Comsol Multiphysics 对上一节方程进行联立求解，即可获得在已知“温-水-土”条件下的寒区渠道不同纵缝设置下的冻胀规律。基于此，深入探索大型弧底梯形渠道“适缝”削减冻胀机理，以求得合理的布设形式。

3.1 有限元网格划分新疆某供水工程渠道设计引水流量120 m3/s，正常水位5.6 m，渠深7.5 m，弧底半径8.47 m，坡比1∶2，C20 混凝土衬砌厚度10 cm，具体断面形式及有限元网格如图3所示。

图3 有限元网格及模型示意（单位：m）

3.2 计算参数渠基土为冻胀敏感性强的粉质黏土，其弹性模量随温度变化［31］，如表1所示。衬砌-基土接触面参数由直剪试验［26］及前期试算［32-33］确定，如表2所示。结合聚乙烯闭孔泡沫板出厂检验报告、聚氨酯砂浆力学试验［34］及文献［28-29］，选取纵缝填充参数如表2所示。其他参数取自文献［17］，如表3所示。地下水位距渠底1.5 m，渠基土初始含水量为20%，未冻土渗透系数为10-7m/s，β 为-8［17］。

表1 冻土弹性模量及泊松比

表2 接触面参数

表3 材料计算参数

3.3 边界条件确定温度边界条件：渠道上表面采用对流热通量边界条件，方程如下：

式中： n 为渠道上边界法向向量； Text、 T 分别为环境温度和地表温度，℃； hc为对流换热系数，W/（m2·℃），与衬砌渠道内风速有关，计算公式如下：

结合当地现场监测数据，渠顶风速取1.83 m/s，渠底风速取1 m/s，二者之间采用二次抛物线函数过渡［13］。环境温度取新疆某地区11月至3月份月平均气温，分别为：-4 ℃、-13.5 ℃、-16 ℃、-13.5 ℃、-5 ℃，冻结期150 d。

工程地区土层表面以下10 ～15 m 处温度常年稳定，鉴于本工程渠深较大，取下边界恒温层深度为15 m，温度值为8 ℃［35］。

位移边界条件：渠道上表面自由，底部边界固定，左右边界施加法向位移约束。

3.4 计算方案计算分为三个部分：（1）首先对上述渠道进行未设缝情况下衬砌板应力变形分析，确定其冻胀变形及受力特征和冻胀破坏规律；（2）以设缝位置、宽度、个数及其组合为变量，分析不同设缝工况对削减冻胀效果的影响规律，探讨“适缝”防冻胀机理；（3）基于上述规律，提出“适缝”的布设方式，包括纵缝位置、宽度和数量的最优组合。

4 结果分析

4.1 大型弧底梯形渠道冻胀破坏特征

4.1.1 温度场结果分析 纵缝对渠道导热性能影响较小，可忽略不计，即是否设纵缝的渠道温度场基本一致。故以渠道未设缝情况下的温度场计算结果（图4）为例进行分析，图中白线为0 ℃等温线。从图中可以看出，渠顶附近存在双向对流换热降温，导致其冻深最大，约为1.5 m 左右；弧底板位置处为单向降温，且受地下水结冰释放潜热影响，冻深最小，约为0.5 m 左右。计算结果满足渠道温度场分布规律［13，15］，冻深值在当地冻深的合理范围内［36］。

4.1.2 大型弧底梯形渠道冻胀破坏特征 衬砌板未设缝情况下，大型弧底梯形渠道变形特点及其截面正应力分布如图5、图6所示。

图4 温度场分布

图5 衬砌板法向冻胀量及变形趋势图（放大系数65）

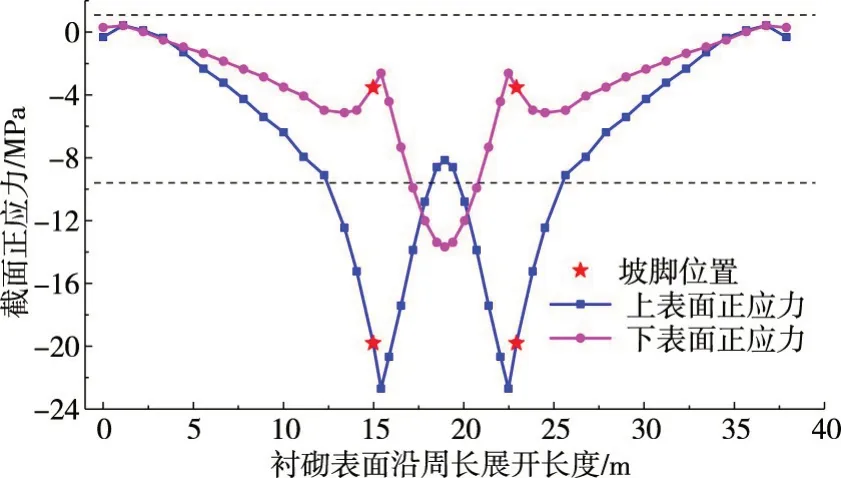
图6 衬砌板截面正应力沿渠周分布曲线

由图5可知，衬砌板在渠基土冻胀变形作用下，呈现出弧底局部向上隆起，坡脚受挤压约束明显，下半段坡板向上挤压，渠口内缩，衬砌整体上抬的变形趋势。弧底板法向冻胀变形量最大，坡脚位置法向冻胀变形量最小，且存在弯曲的变形趋势。结合其正应力分布（图6）可知，在冻胀力作用下，弧底段“反拱”的拱效应使其整体以受压为主，同时，现浇一体化边坡衬砌板在坡脚附近上表面挤压应力值最大；在坡板下半段，向上的挤压变形导致其上下表面仍以受压为主；而在上半段接近渠顶位置，呈现由上下表面同时受拉，转变为上表面受压、下表面受拉的弯曲状态。其中，上、下表面压应力极值分别出现在坡脚附近（23 MPa）和弧底中心（14 MPa），均大于混凝土强度设计值，易出现挤压破坏，同时，渠顶衬砌板下表面产生的拉应力可能会产生拉裂破坏，这与工程现场渠道衬砌破坏位置基本一致［37-38］，另外北疆车排子西干渠的大型弧底梯形渠道的冻胀破坏位置亦多在此［39］，表明数值模型的计算结果与实际基本一致，可满足工程要求。

4.2 纵缝位置及缝宽削减冻胀效果分析

4.2.1 纵缝位置削减冻胀效果分析 纵缝可减少板间约束，削减渠道冻胀破坏。为探究纵缝位置对渠道防冻胀效果影响，结合《规范》，以纵缝宽度1 cm 为例，基于上一节结果，在应力值较大位置处（弧底中心、坡脚、1/4 坡板位置）设缝，衬砌板正应力分布如图7所示。纵缝位置除弧底中心外，其余均为渠道衬砌板左右对称设缝。

图7 不同纵缝位置衬砌板截面正应力沿渠周分布曲线

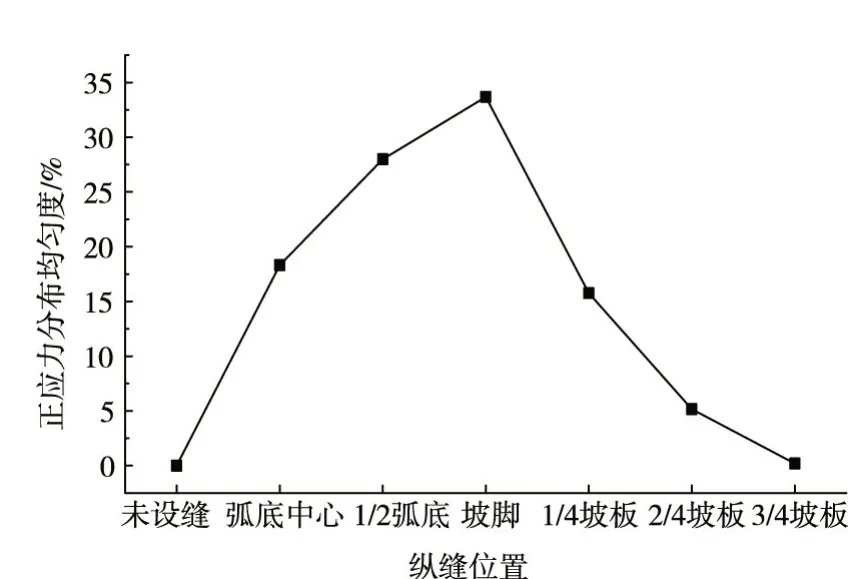
图8 正应力分布均匀度随纵缝位置变化曲线

由图7可知，纵缝可显著减少衬砌板受到的压应力值，逐渐靠近强度安全区域，拉压应力极值差减少，自身受力均匀化。但会导致上半段坡板拉应力区增大，尤其是上表面拉应力值较大。

坡脚设缝可最大程度地减少压应力极值，削减衬砌板应力达47.6%，效果最好；随着纵缝位置远离坡脚，上、下表面压应力极值逐渐增加，远离强度指标。

从弧底中心开始，向渠顶方向移动设置纵缝，其上下表面平均正应力分布均匀度如图8所示。

从图8可以看出，衬砌板设缝均可提高正应力分布均匀度，改善应力状态，防冻胀效果较好，其效果与纵缝设置位置关系极大。随着纵缝位置远离弧底中心，正应力分布均匀度逐渐增加，至坡脚位置时，正应力分布均匀度最大，为33.7%；随着纵缝位置远离坡脚，正应力分布均匀度逐渐降低，至3/4 坡板位置时，基本无变化。

结合上述分析可知，正应力分布均匀度可准确描述出衬砌板正应力数据分布的离散程度，可直观反映出衬砌板适应冻胀变形的能力和纵缝削减冻胀的效果，结合强度指标亦可判断衬砌板是否发生破坏，表明采用上述两级评价指标更为合理，可综合分析“适缝”防冻胀的效果。

综合衬砌板正应力分布均匀度及其正应力分布可知，坡脚设缝防冻胀效果最好，随着纵缝位置从坡脚向渠顶方向或从坡脚向弧底中心移动时，削减冻胀效果逐渐降低，但需注意设缝所导致的较大拉应力值问题。

4.2.2 纵缝宽度削减冻胀效果分析 选取衬砌板的典型位置设缝，即弧底中心、坡脚、1/4 坡板位置处，取纵缝宽度为1 ～3 cm，衬砌板上下表面平均正应力分布均匀度如图9所示。

由图可知，正应力分布均匀度随纵缝宽度的增加而逐渐增加，坡脚纵缝宽度达1.5 cm，弧底中心纵缝宽度达2.5 cm 后，基本趋于平稳。而坡板纵缝宽度对正应力分布均匀度影响很小，宽度1 cm 即可满足要求。坡脚设缝正应力分布均匀度最高，为46.4%，而坡板设缝最低，为16.8%。对上述不同纵缝宽度衬砌板表面最大拉、压应力值进行分析，如图10所示。

由图可知，单独设缝时不论何处设缝，随着纵缝宽度的增加，衬砌板最大压应力值均随之减少，而最大拉应力却缓慢增大。坡脚纵缝宽度为1.5 cm 时，虽然局部拉应力较大，但最大拉、压应力最靠近衬砌板强度安全区域；弧底中心和坡板设缝都偏离强度安全区域较远。

图9 衬砌板正应力分布均匀度随纵缝宽度变化曲线

图10 衬砌板截面正应力值随纵缝宽度变化曲线

综合正应力分布均匀度及其正应力分布可知，单独设缝时坡脚设缝削减冻胀效果最好，而后为弧底中心或坡板位置。但缝宽选择需慎重，尤其是弧底中心设缝，以减少额外的拉裂破坏。

不同宽度纵缝位置处变形值如表4所示，纵缝以吸收板间挤压变形为主，切向变形为辅，从而改善衬砌板受力。但其变形值较小，即该措施以减少衬砌板受到的冻胀力为主，而对冻胀变形无明显影响。纵缝的挤压变形值随宽度增加而逐渐增大，至一定宽度后，不再变化。坡脚纵缝宽度为1、1.5 cm 时，挤压应变值大于纵缝的极限压应变，即此时纵缝的宽度并不能将衬砌板的挤压变形完全吸收掉，板间推力依然较大；在宽度为2 cm 时，纵缝挤压位移增加很小，且并未达到极限压应变，说明此宽度已可将板间挤压变形完全吸收掉，结合3 cm 宽度结果可知，再增加缝宽将不会进一步吸收挤压变形。结合下表可知，弧底中心纵缝最大宽度2.5 cm，坡板1 cm 基本可满足要求，与应力分布均匀度及正应力分布结果一致。

4.3 纵缝个数及其组合削减冻胀效果分析不同纵缝位置处吸收衬砌板挤压变形值决定了衬砌板的受力状态，对削减冻胀效果影响较大。本节拟采用组合设缝方式，纵缝位置组合：弧底+坡脚，弧底+坡板，坡脚+坡板，弧底+坡脚+坡板，组合中每种纵缝的宽度皆一致。结合上文结果，以弧底中心代表弧底设缝位置，1/4 坡板代表坡板设缝位置，纵缝宽度拟分别取1、1.5、2 cm，其正应力分布均匀度及最大拉、压应力值如表5所示。同时以纵缝宽度1 cm 为例，对其正应力分布情况进行分析，如图11所示。

由表11可知，相比于单独设置等宽度纵缝情况下，组合设缝均能进一步减少衬砌板受到的压应力值，应力分布均匀化，削减冻胀效果增加。

随着组合纵缝的总宽度增大，压应力极值削减幅度逐步增加，正应力分布均匀度及拉应力极值呈增大趋势。结合图11可知，在纵缝宽度为1 cm 的情况下，坡脚上表面及弧底中心下表面压应力极值减少，拉应力过大值主要发生在弧底中心和坡板上表面及坡脚附近下表面。

结合表5、图11可知，弧底+坡脚组合设缝正应力分布均匀度最大，但局部位置拉应力值过大；坡脚+坡板组合设缝次之，二者正应力分布均匀度相近，且最大拉应力值较小；弧底+坡板组合设缝下衬砌板的应力分布均匀度最小，且在纵缝宽度较大时，拉应力值过大。相较于两种纵缝位置组合设缝，弧底+坡脚+坡板组合设缝下正应力分布均匀度及拉、压应力值变化不大，效果并不显著。

综合正应力分布均匀度及强度指标，坡脚+坡板组合设缝最优，在具体工程应用时，应在满足混凝土强度指标的基础上保证应力分布均匀度最大，即为纵缝的最优布置方式。

4.4 “适缝”防冻胀措施工程应用基于上述分析结果，对上述新疆某大型供水渠道的最优纵缝布置形式进行计算。

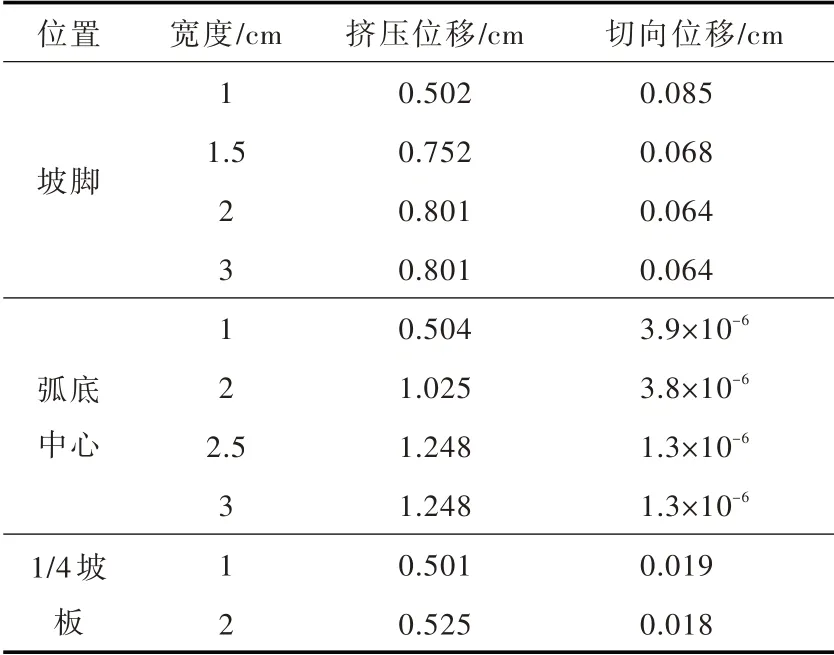
表4 纵缝处变形值

表5 正应力分布均匀度S 及最大拉、压应力值

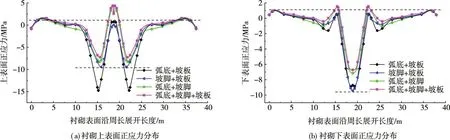
图11 纵缝宽度1cm 时衬砌板截面正应力沿渠周分布曲线

由图7、图10可知，单独设缝无法使衬砌板应力满足强度要求。由表5及图11可知，坡脚+坡板组合设缝可使压应力满足要求，且拉应力超强度值不大。经过计算，得出纵缝最优布置方式：坡脚+1/4 坡板+3/4 坡板组合设缝，缝宽皆为1 cm，此时衬砌板截面拉应力为0.57 MPa，压应力为9.47 MPa，冻胀应力削减50%以上，应力分布均匀度最大为43.8%，满足两级指标要求。

5 “适缝”防冻胀机理探讨

以坡脚、弧底中心设缝为例，分析其轴力及弯矩沿渠周分布情况，对“适缝”防冻胀机理进行分析，如图12所示。

由图12可知，设缝与不设缝时坡脚附近出现最大正弯矩，而弧底中心出现最大负弯矩值；缝宽增加，弧底最大负弯矩逐渐增加，但坡脚设缝最大正弯矩及轴向压力削减得更快。

随着缝宽增加，坡板处轴向拉力增加，压力减小；弧底设缝不仅使坡板顶部以拉为主，弧底也可能出现拉力，而坡脚设缝弧底不出现拉力区。

轴力图呈现“W”形分布，而弯矩图呈现“M”形分布，从构件受力来看上部坡板属于受拉杆件，下部坡板为压弯梁构件，弧底板为两端正负弯矩作用的压弯曲梁构件。

渠道纵缝可吸收冻胀变形，结合轴力、弯矩分布对衬砌结构进行模型概化：纵缝可视为弹性铰支座，缝宽增大刚度减少；未设缝时，弧底段为无铰拱，坡板为承受轴压和横向冻胀力作用下坡脚固支、坡顶简支的超静定梁；弧底中心设缝，可视为拱顶设弹性铰的曲梁，坡板结构不变但跨度增大；坡脚设缝，弧底板可视为坡脚设弹性铰的两铰拱，坡板简化为承受轴向推力和法向冻胀力的两端铰支梁；设缝位置沿坡板从弧底向坡顶移动可视为不断缩短坡板简支梁间距和延长弧底段拱脚长度，最终不断调整衬砌结构刚度和内力分布，达到优化衬砌结构体系防冻胀破坏能力的目的。

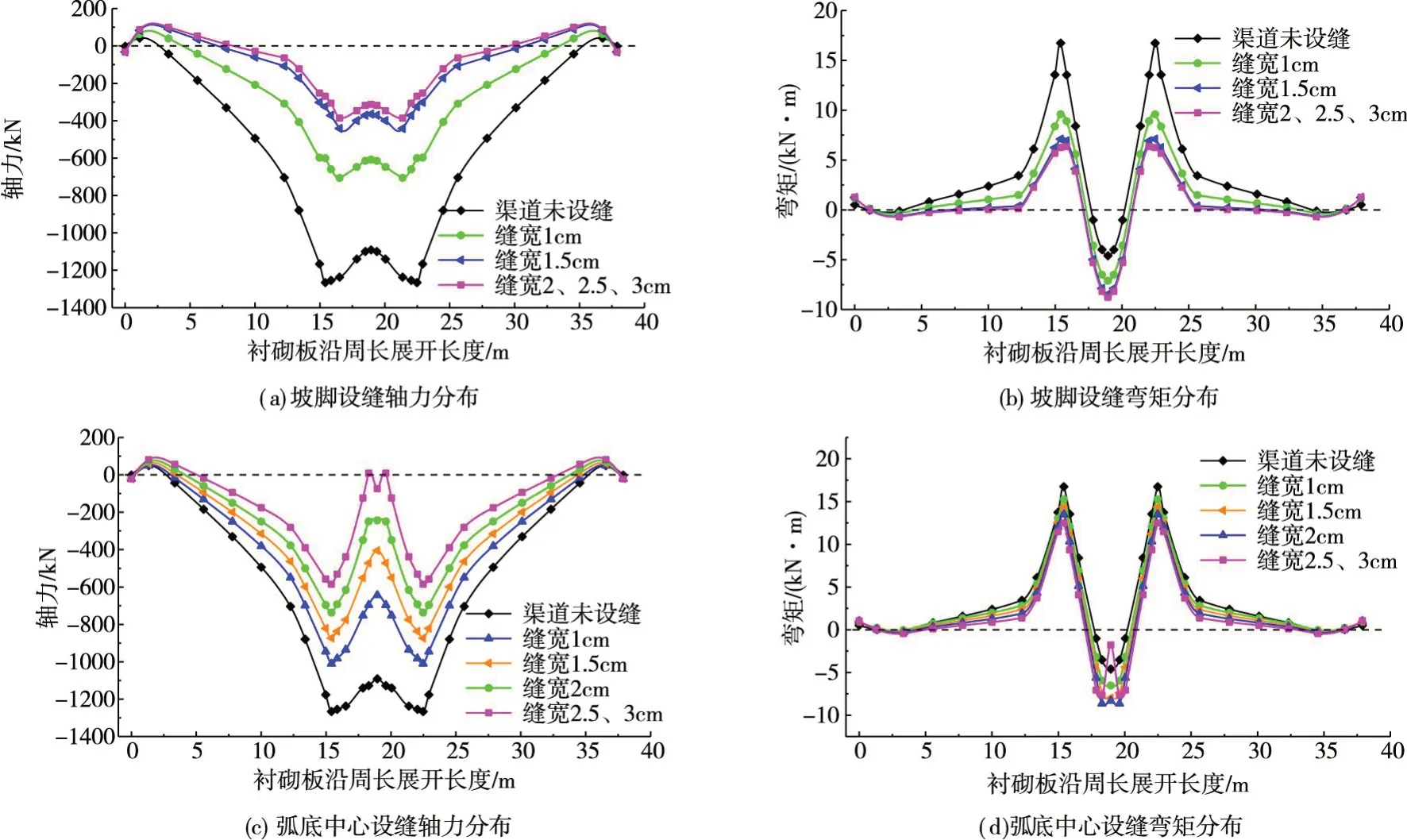
图12 衬砌板内力沿渠周分布曲线

6 结论

考虑冻土的横观各向同性冻胀特征，对水-热-力三场耦合模型进行修正，并提出了衬砌-基土及纵缝填充的接触本构，建立了寒区渠道设纵缝防冻胀分析模型，基于正应力分布均匀度及强度指标，对大型弧底梯形渠道“适缝”防冻胀机理进行了探讨，对纵缝的合理布设方式进行了研究，结论如下：

（1）寒区大型弧底梯形渠道衬砌板的“W”形轴力分布及“M”形弯矩分布特征，使弧底中心下表面及坡脚上表面易产生挤压破坏，在弧底中心上表面及坡脚下表面易产生拉裂破坏。

（2）弧底拱效应及坡板的强制位移约束使衬砌板以受压为主，弧底衬砌板-坡板可概化为薄拱-梁结构，纵缝为可移动弹性铰，纵缝位置及宽度的变化不断调整拱-梁结构的刚度及弹性铰的约束刚度，以适应基土冻胀变形，使衬砌板表面应力均匀化，从而削减冻胀。

（3）随纵缝宽度的由小增大防冻胀效果更好，但缝宽度大于1.5 cm 后，会过度削弱弧底拱效应，使弧底中心和坡板上表面及坡脚附近下表面拉应力过大，易产生拉裂破坏。

（4）纵缝防冻胀效果与其位置关系极大，单独设缝时坡脚位置设缝最佳，纵缝宽度为1 cm 时，削减衬砌板正应力值达47.6%，应力分布均匀度为33.7%，随着纵缝位置远离坡脚，削减冻胀效果逐渐减弱。

（5）组合设缝削减冻胀效果优于单独设缝，尤以坡脚与坡板组合设缝最优；在坡脚+1/4 坡板+3/4坡板处组合设缝，缝宽取1 cm，此时截面拉应力为0.57 MPa，压应力为9.47 MPa，正应力值削减50%以上，正应力分布均匀度为43.8%，满足强度指标，综合防冻胀效果最好。