考虑回水顶托影响的梯级库群日前调峰MILP模型

赵志鹏，刘 杰，程春田，廖胜利，靳晓雨

（大连理工大学，辽宁 大连 116024）

1 研究背景

我国正处于经济结构改革的过渡期，加之清洁能源的大规模投产，电力系统面临巨大的调峰压力，水电作为一种可调节的清洁能源需要承担更大的调峰任务［1-4］。水调系统信息化程度的提高对水电短期调度精细化的要求越来越严格［5］，尤其对于有灵敏水力联系的梯级库群，不仅水库运行状况（如出力、振动区、最大发电流量、水头损失等）对水头极为敏感，而且梯级之间还存在敏感的水力耦合，以往将一日内水头设为定值或采用平均水头进行日调度的粗放模式难以满足精细化调度的要求，因此需要充分考虑日内的水头变化。其中回水顶托是存在于耦合梯级库群间的一种复杂的水力联系，正常情况下，水库的尾水位和出库流量存在一条稳定的关系曲线，但当梯级水库上下游坝址较近时，较高的下游库水位产生回水，上游水库的尾水位于回水区间内时，上述稳定的水位流量关系曲线将被破坏，这就是所谓的回水顶托影响［6-8］，回水顶托在我国西南水电库群间普遍存在，如三峡-葛洲坝，溪洛渡-向家坝，天生桥一级-二级等。回水顶托的直接影响是抬高上游水库尾水位，如果在日前调度计划中未将其考虑在内，将导致上游水头计算偏高与实际运行工况不符，对于上下游电站有利益冲突的梯级，甚至会导致计划发电量与实际发电量存在冲突而产生经济纠纷［9］。因而，针对有灵敏水力联系的梯级库群，如何将下游回水顶托的影响考虑到模型中，并实现模型的高效求解，是当前水库精细化调度的重点及难点之一。

水电日前调峰优化调度需要同时考虑电网、水库及机组多重约束，本质上属于复杂的多维、动态、非凸、非线性规划、强耦合问题［10］。将回水顶托影响考虑到模型之后，该问题的耦合性、非凸、非线性等特征进一步凸显，极大地增加了求解难度。目前短期调峰模型的研究较多，通常采用余荷均方差最小或余荷最大值最小为目标建立模型，由于目标函数的特殊性多采用启发式搜索方法［11-13］，解的稳定性难以保障，且大多研究简化水头计算，将回水顶托对发电水头的影响考虑在内的研究少之又少。文献［14］在解决三峡机组组合时考虑葛洲坝回水顶托影响，在葛洲坝水位已知的情况下拟合二维水位流量曲线并采用迭代法求解尾水位；文献［15］虽然考虑了电站出力的水头敏感性，但其尾水位的计算或采用定值或采用下游电站坝上水位；文献［16］提出了回水顶托的三维关系曲线，根据下游坝上水位的范围采用二进制变量选取某个水位流量曲线，进而将三维关系转换成二维关系进行求解，但其求解精度存在一定的偏差。目前调度机构在进行日前调峰计划编制时，大多将一日划分成96 个时段进行调节计算。而以上研究虽在一定程度上考虑了回水顶托对调度的影响，但由于调峰问题及复杂水力耦合本身存在的复杂性或所采用算法本身的局限性，大多将一日简化为24 个时段进行优化计算，计算结果的实用性相对较差。

混合整数线性规划（MILP）是水库发电调度领域最为常用的数学规划算法之一［17-19］。相较于传统的启发式算法，MILP 具有理论成熟，结果稳定性及全局收敛性好，以及有大量先进的开源及商业求解器可以直接调用等特点。因此，本文建立考虑回水顶托影响的梯级库群日前调度的96 点混合整数线性规划（MILP）模型。模型以余荷平均距平绝对值最小为目标，通过函数聚合方式减少常规及有回水顶托水库的非线性因素。聚合后，常规水库和有回水顶托水库的非线性因素分别转化为三维曲面约束和四维超曲面约束，并引入SOS2（Special Order Set of type 2）约束建模方法对其进行线性化处理。最后以西南流域某梯级为例进行验证所提算法及模型的有效性。

2 数学模型

2.1 目标函数采用余荷平均距平绝对值最小为目标函数以平缓负荷峰谷差：

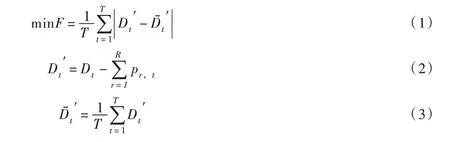
式中： r 为电站自上游至下游编号； R 为总电站数； t 为时段编号；T 为总时段数，本文将一天划分为96 个时段； Dt为时段t 系统面临负荷； D′t为时段t余荷；为余荷平均值； pr,t为电站r 在时段t 出力，如无特殊说明，下文r 均代表电站编号，t 均代表时段编号。

目标函数中包含绝对值符号难以直接利用MILP 求解，引入非负辅助变量δt后，目标函数可等价转化为：

2.2 约束条件

（1）梯级日总电量约束：

式中： Δt 为时段间隔； E 为梯级日总电量。

（2）水量平衡约束：

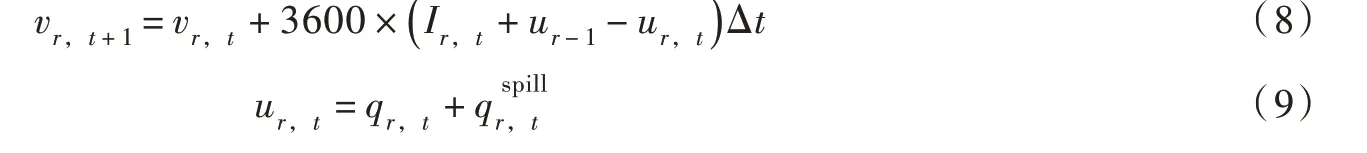
式中：vr，t为库容；Ir，t为区间入库流量；ur，t为出库流量，包括发电流量qr，t及弃水流量

（3）出力曲线约束：

（4）水位库容约束：

（5）尾水位曲线约束：

（6）净水头计算公式及水头损失约束：

式中： Δhr,t为电站r 在时段t 的水头损失； ar为水头损失系数。

（7）电站出力约束及爬坡约束：

（9）弃水流量约束：

（10）出库流量约束：

（11）库容约束：

（12）日调节水库末库容约束：

3 求解方法

3.1 多约束曲线聚合模型中存在诸多非线性因素，难于直接利用MILP 进行求解，分段线性化是MILP 求解非线性约束时常用的处理方法。模型中非线性约束包括式（10）—（12）和式（14）等。以往研究大多对这些约束直接进行线性化，每个约束的线性化过程均会引入大量0-1 整数变量，从而极大影响求解效率，甚至无法求解。为了避免引入过多的0-1 整数变量，分别针对常规无回水顶托水库和有回水顶托水库提出如下约束聚合策略：

3.1.1 无回水顶推水库约束聚合 对于常规无回水顶托水库，将式（10）—（14）进行聚合可得：

实际调度中要避免发生弃水，因而本文设定弃水流量为0，则ur,t=qr,t，对式（22）中相应部分进行替换可得：

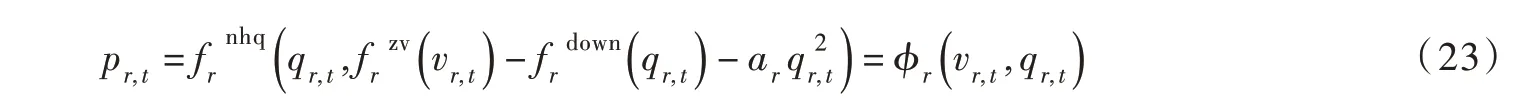
3.1.2 有回水顶推水库约束聚合 对于有回水顶托水库，将式（10）—（14）进行聚合可得：

式中，φ′i( )将( vr,t,qr,t,vr+1,t,pr,t)约束在四维空间的超曲面上，并包含了有回水顶托水库模型中所有的非线性项，本文称之有回水顶托水库的等效动力函数，简称顶托动力函数。本文利用约束式（26）对有回水顶托水库模型约束式（10）—（14）进行等效替换。

3.2 等效动力函数线性化常规动力函数为三维曲面函数，此类函数的线性化方法以往已有大量文献进行研究［20］。对于顶托动力函数，本质为四维超曲面函数，极大的增加了建模难度。本文引入SOS2 约束建模方法统一对这两种动力函数进行线性化。为简化表达，首先定义NI为不大于I的正整数集合，ℕ0I为不大于I的非负整数集合，

3.2.1 SOS2 约束 SOS2 是一种特殊的非负实数集合，该集合只允许出现至多两个非零实数，且这两个非负实数必须是在顺序上是相邻的。定义有序实数集合对ηS施加SOS2 约束（表示为SOS2（ηS）），ηS即成为集合。当S ＞1 时，SOS2（ηS）可以如下方式建模：

式中： bs为指示变量，如果bs=1，则表示除ηs-1≥0 ，ηs≥0 外，ηS中其他元素必须为零。如果S=1，则SOS2（ηS）退化为下式：

通过SOS2 约束建模方式，可以进一步构建常规及顶托动力函数的线性化方法。

3.2.2 常规等效动力函数线性化 常规等效动力函数是一个典型的非凸三维曲面，常用的线性化方法主要包括两类：一类是将曲面在其中一个维度上划分成若干区间，然后在相应区间上用一个一维曲线近似表示，该方法建模比较直观，引入的二进制数量相对较少，但精度不足［18，21-22］。另一类是利用三角栅格化技术将曲面划分成若干三角网格，利用三角网格顶点的凸组合近似表示相应区域的曲面，该方法求解精度高，但是会引入大量0-1 整数变量，从而影响求解效率［14，23］。本文采用基于四边形网格栅格化技术与SOS2 约束建模方法对常规等效动力函数进行线性化处理。

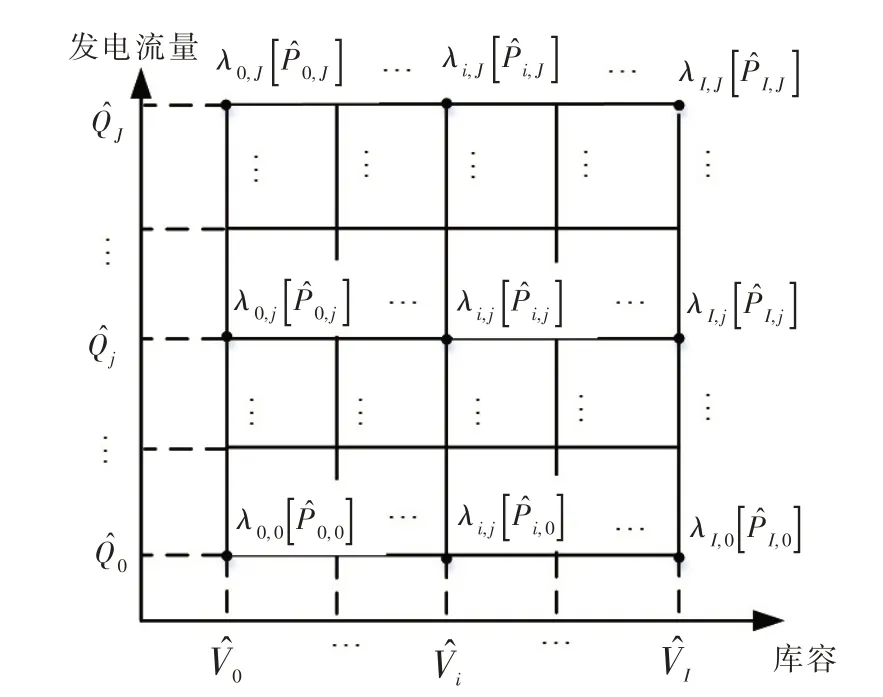
图1 常规动力函数图像在库容-发电流量平面投影

图1为常规动力函数图像在库容-发电流量平面的投影示意图。为便于表达，变量、函数及常量均省略电站编号r 及时段编号t 下标（下同）。如图所示，栅格化时设置为库容及发电流量坐标方向上栅格化的格点集合，且满足其中I 和J 分别为库容及发电流量方向栅格化区间数。图中表示对应格点的出力值。引入λi,j非负辅助变量为格点的权重系数。则具体构建方法如下：

图2 顶托动力函数在库容-发电流量-下游库容三维空间投影

3.2.3 顶托等效动力函数线性化 顶托动力函数本质是一个四维非凸超曲面函数，这进一步增加了建模难度。本文利用直六面体栅格化技术和SOS2 约束建模法对该函数进行线性化处理。

图2为顶托动力函数四维曲面在库容-发电流量-下游库容三维空间的投影示意图，其中v′为下游水库库容。与常规动力函数类似，栅格化时除设置为库容及发电流量坐标方向上栅格化格点集合外，进一步设置为下游库容坐标方向的栅格化格点集合，且满足其中K 为下游库容方向的栅格化间隔数，分别为下游水库库容下限及上限值。引入λi,j,k非负辅助变量为格点的权重系数。具体构建方法如下：

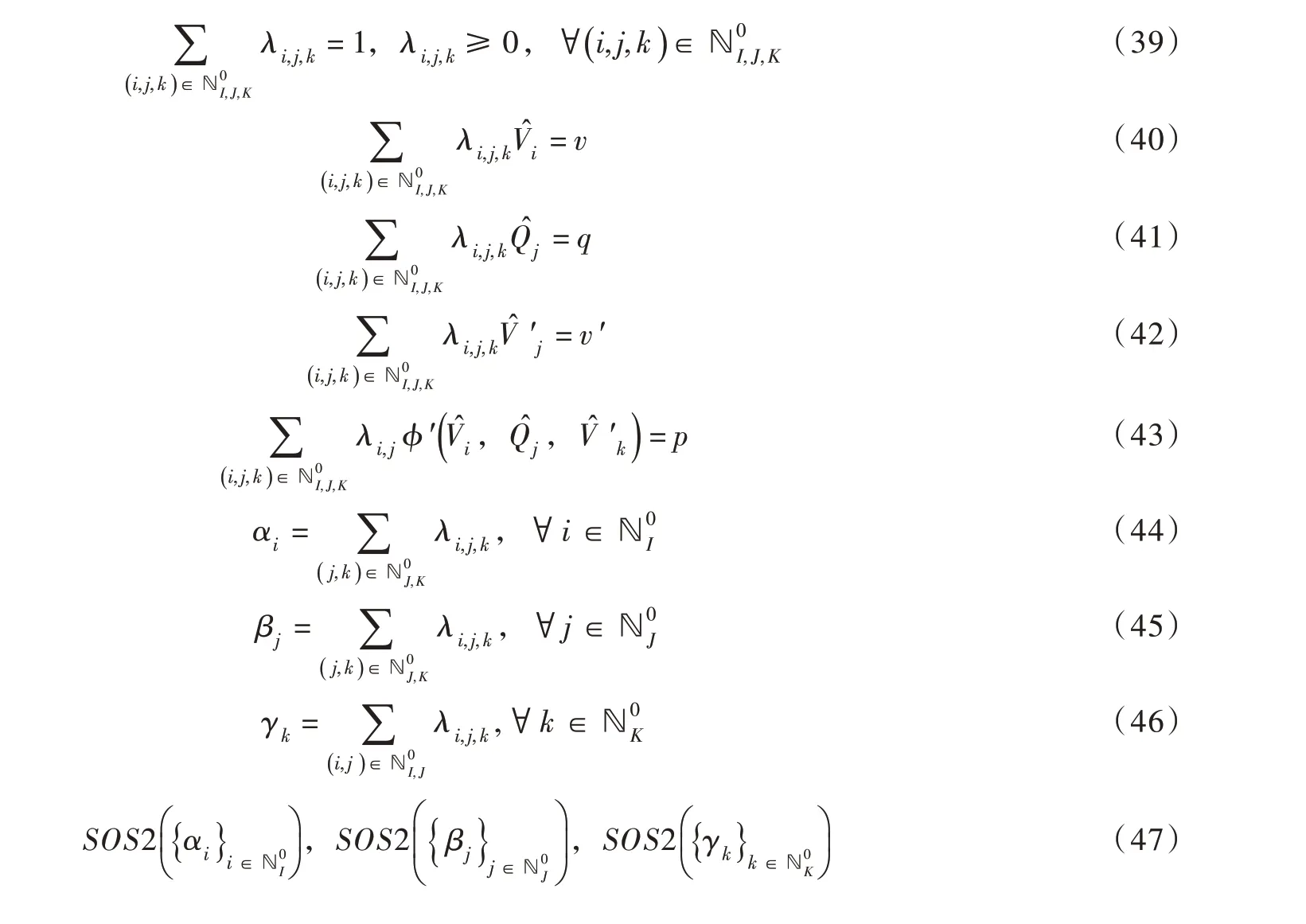
其中式（40）—（43）将( v ,q,v′,p )表示成四维点集的凸组合。αi，βj，γk为引入的表达式变量，分别表示图2中所示的库容方向法平面i ，发电流量方向法平面 j ，下游库容方向法平面k 的上格点对应权重之和。式（47）依次表示对库容，发电流量，下游库容方向上各法平面权重施加SOS2 约束。在SOS2 约束下，至多允许库容方向相邻两个法平面，发电流量方向相邻两个法平面以及下游库容方向相邻两个法平面上格点对应权重非零。取交集后，最终仅允许相邻8 个格点对应权重非零。此时点( v,q,v′,p )被限制在这8 个格点最小凸包内部。当栅格化格点足够多时，点( v ,q,v′,p )将无限趋近于顶托等效动力函数四维超曲面。

4 应用算例及分析

4.1 场景选择与模型参数设置本文选择西南某流域电站A、电站B 组成的梯级库群为研究对象，电站A、B 是南方电网重要的调峰调频电源，坝址距离仅为7 km，电站A 位于电站B 的回水区间内。电站A 调节性能为不完全多年调节，总装机1200 MW；电站B 调节性能为日调节，总装机1320 MW。模型均采用Python3.6 语言进行编写，并调用Gurobi8.1 商业求解器MILP 分支定界算法进行求解。程序运行环境为Ubuntu16.4 虚拟机，硬件配置为Intel（R）Xeon（R）CPU E7-4850 v3 @2.20GHz 96 logic cpu，32G RAM。所有模型设置最大计算时间为3600 s，gap 参数设置为0.01，gap计算公式见下式：

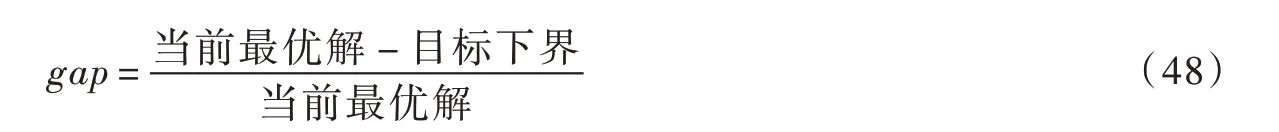
采用如下累积误差公式衡量模型线性化精度：

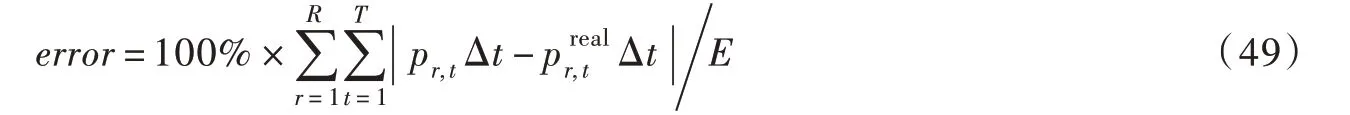
本文所提模型命名为本文模型，设置常规模型为对照组，常规模型直接采用传统方法进行建模。传统方法是指不经过聚合，直接对2.2 节中非线性约束进行分段线性化建模的方法［19，24］。其中单变量非线性约束采用文献［24］中的方法进行建模，双变量非线性约束采用3.2.1 节中介绍的方法进行建模。模型中非线性约束相应自变量分段线性的分段数设置见表1。由于水库A 调节性能为不完全年调节，在一天内的库容变化较小，因此本文仅在其初始水位上下1 m 的库容范围内进行离散，分段数设为1。其余变量均在其最大与最小值之间进行均匀分段。经过聚合后，本文模型各水库不再包含水位、净水头等变量，表格中相应内容用“-”表示。

表1 各变量分段数目

为体现算法通用性，选取该梯级历史2月、3月、7月、8月典型日实际数据进行一天96 点模拟计算，其中2、3月为枯期代表，7、8月为汛期代表。电站B 为日调节电站，末水位等于始水位，实现日内周期调节，各月份方案参数见表2。

4.2 结果分析对4 种典型日场景下均采用本文模型和常规模型进行建模计算，表3为本文模型及常规模型中连续变量，约束及离散变量总个数。从表3可以看出，通过聚合方式，本文模型的变量和约束数量均显著小于常规模型，这为本文模型的高效求解提供了基本保障。

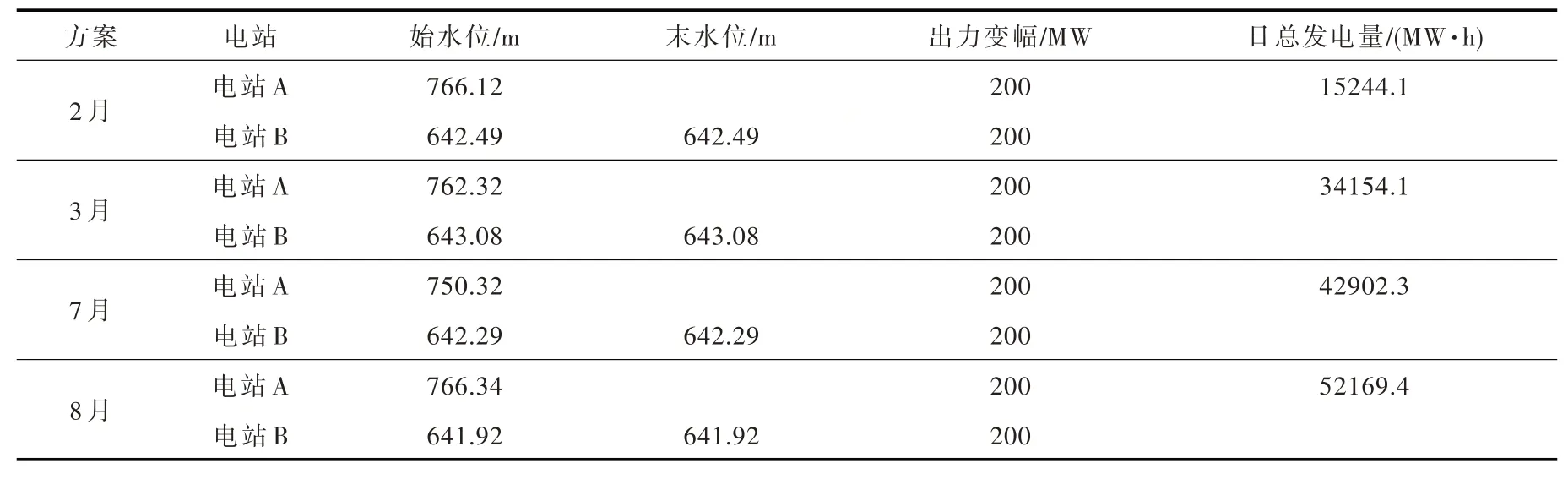
表2 各方案参数设置

表3 本文模型和常规模型中约束及变量总个数

4.2.1 调峰效果分析 图3给出了本文模型在4 种场景的削峰结果图，均达到不同程度调峰效果。进一步分析结果指标，如表4所示，由计算结果可知，本文模型在满足电量约束且不发生弃水的条件下均能找到可行解。枯期梯级总电量要求较小，均达到较好的调峰效果，2月、3月峰谷差减小率达31.41%和35.05%，达到较好的调峰效果；而汛期在不发生弃水的环境下，调峰能力有限，7月、8月峰谷差减小率仅为17.00%和1.00%。因而，在梯级日总电量较大的情况下，不弃水与调峰存在矛盾，而本文模型均能在不弃水条件下找到可行解。

表4 典型日场景调峰结果

图3 本文模型各月份调峰效果

4.2.2 回水顶托效果分析 选取3月的计算结果对回水顶托影响进行分析。图4（a）以出库流量为参照，考虑回水顶托和不考虑回水顶托尾水位对比图，图4（b）以下游坝上水位为参照，考虑回水顶推和不考虑回水顶推尾水位对比图。考虑回水顶托的结果由本文模型进行计算，不考虑回水顶托的结果是根据本文模型计算结果的下泄流量过程进行反推计算出的结果。从图4可以看出，不考虑顶托的尾水位趋势与出库流量一致，不受下游坝上水位影响。考虑顶托之后，尾水位同时受下泄流量及下游坝上水位影响，整体趋势与下游坝上水位趋势一致，因而电站A 的尾水位受下游电站坝上水位影响极大，在日常调度模型构建中不可忽略。表5给出了详细的指标计算结果，可以看出，不考虑顶托与考虑顶托，水库A 的水头差距达4.67 m，累计多发电量433.14 MW·h，累计误差达2.84%，实际操作若不考虑回水顶托，必然造成计划与实际工况不符，不能按预期完成调度任务。

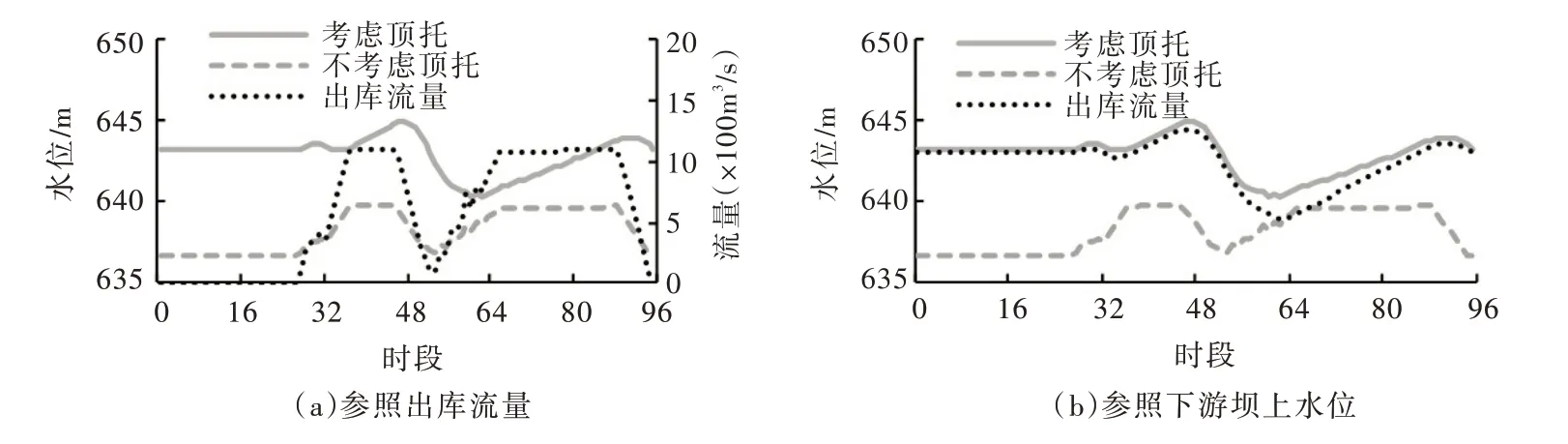
图4 考虑回水顶托与不考虑回水顶托尾水位对比

表5 水库A 考虑顶托与不考虑回水顶托计算差异对比

4.2.3 计算效率与精度分析 表6列出了本文模型，常规模型在4 种典型日场景中计算结果。设置最长计算时间为3600 s，表中gap 为“-”时，表示没有在设定时间内算出可行解。从两个模型的求解时间可以看出，本文模型在各个月份情形下均能够算出有较高精度的可行解，且大部分月份（2、3、7月份）可以在较短时间内算出满足gap 要求的最优解；常规模型仅2月份在3006 s 算出满足gap 的可行解，3月份在设定时间内甚至没有得到可行解，由此可见，本文模型的计算效率要显著优于常规模型。对比目标值可以看出，本文模型在大部分月份求解的目标值要优于传统模型。对比累积误差可以看出，各场景下常规模型的累积误差均大于本文模型的累积误差。因此，本文所建模型无论在精度还是计算时间及算法稳定性上都优于常规线性化模型，对MILP 在实际工程中的应用具有重要意义。在实际应用时，对于求解时间敏感的应用场景，可以通过适当减少最长运行时间限制或者提高gap 值的方式进一步降低总体运行时间。

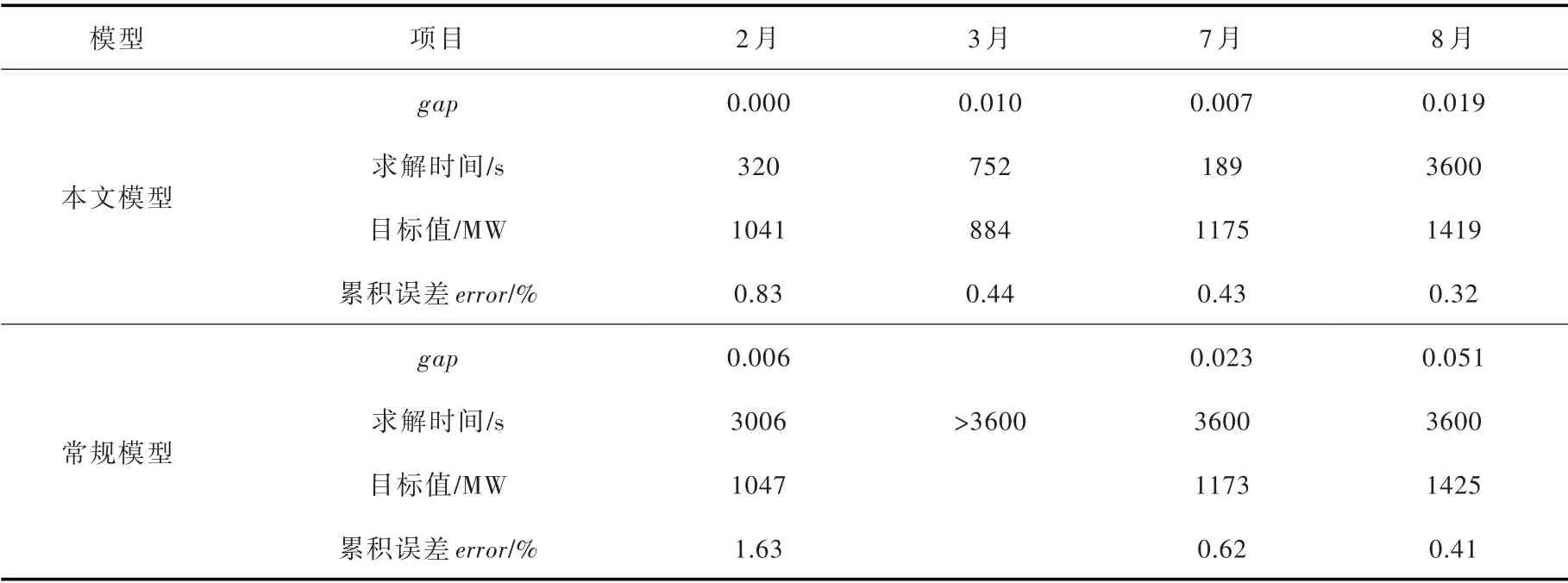
表6 典型日场景计算结果

5 结论

为处理梯级库群间存在的强耦合水力联系，采用考虑下游坝上水位的尾水位计算公式将回水顶托影响考虑到模型当中，把梯级库群调度中多个非线性约束聚合成单个等效动力特性曲线，借助SOS2 约束对模型进行线性化，与传统线性化方法相比，显著减少了模型中的连续变量及离散变量数目，提高了模型的求解效率及精度。以西南某存在回水顶托的梯级库群为例对所提模型及算法进行验证，无论在求解精度还是求解效率上都优于常规MILP 模型，对比考虑与不考虑回水顶托模型计算结果，不考虑回水顶托影响所制定的计划造成较大累积误差，因此，针对存在回水顶托的梯级库群制定调峰日计划时必须将其考虑在内。