管道水力摩阻系数的敏感性分析

郭永鑫，郭新蕾，杨鹏志，付 辉，王 涛

（1.中国水利水电科学研究院 流域水循环模拟与调控国家重点试验室，北京 100038；2.河北水利电力学院，河北 沧州 061001）

1 研究背景

管道输水具有效率高、环境影响小、拆迁占地少、运行调度安全可靠、维护管理简单等特点，广泛应用于城市给排水、农业灌溉、跨流（区）域调水等水利工程中。管道水力计算公式及其摩阻系数的合理选用是流体输送工程设计的关键，其选取合理与否直接影响水力计算成果的精度，进而影响工程的总体布局、设计规模、投资乃至运行费用。现有规范和工程设计常用的水力计算公式及相应的摩阻系数有［1-2］：达西-魏斯巴哈（Darcy-Weisbach）公式和达西摩阻系数λ，海森-威廉（Hazen-Williams）公式和海森-威廉系数Ch，谢才-曼宁（Chézy-Manning）公式和曼宁糙率系数n。

大量研究和工程实践表明水力摩阻系数不仅与管道内壁的粗糙度有关，而且受管径D、流速V、水流黏滞系数ν等的影响［3-4］。然而，国内现有规范给出的摩阻系数取值范围较宽，对摩阻系数影响因素的考虑不全面，导致工程设计，尤其是大口径输水管道的摩阻系数精确取值困难，部分工程的水力计算误差较大。例如，新疆北疆供水工程小洼槽倒虹吸，采用DN3100 玻璃钢夹砂管，曼宁糙率系数设计值n=0.0090，工程运行后实测n=0.0106，比设计值大18%，导致上下游进出口水位差比设计值增加0.6 m，不能满足设计输水流量要求［5］；三个泉倒虹吸采用钢管和PCCP 管的组合方案，其中DN2700 环氧内衬钢管的曼宁糙率系数设计值n=0.0120，实测n=0.0098，比设计值小23%，DN2800PCCP 管道的曼宁糙率系数设计值n=0.0135，实测n=0.0108，比设计值小25%，实际过流能力大于设计值，原设计方案偏于保守［6］；南水北调中线北京段DN4000PCCP 管道，曼宁糙率系数设计值n=0.0120，实测n=0.0101，比设计值小15%，实际运行水头损失（5.30 m）仅为设计值（7.64 m）的69%［7］。

因此，有必要通过建立不同水力摩阻系数间的换算关系，系统分析各摩阻系数对不同因素的敏感程度和变化规律，进而提出工程中水力计算公式选用和摩阻系数取值应注意的问题。

2 管道水力计算公式

2.1 达西-魏斯巴哈公式

式中：hf为管道沿程水头损失，m；λ为达西摩阻系数；D 为管道内径，m；L 为管段长度，m；V 为管道平均流速，m/s；g 为重力加速度，m/s2。达西-魏斯巴哈公式适用于不同流体（气体或液体）的不同流态（包括层流和紊流），达西摩阻系数λ通常采用柯尔勃洛克-怀特（Colebrook - White）公式计算：

式中：k 为当量粗糙度，m；Re 为雷诺数。柯尔勃洛克-怀特公式是计算紊流区达西摩阻系数λ的半理论半经验公式，其适用范围涵盖了光滑管区、紊流过渡区和粗糙管区，大量的试验结果表明该式与实际商用管道的阻力试验结果吻合良好，被公认为是管道水力计算的标准方程［8］。

当水流处于紊流粗糙区时，雷诺数Re足够大，式（2）可简化为尼古拉兹（Nikurasde）粗糙管区公式：

2.2 海森-威廉公式

式中：Ch为海森-威廉系数；Q 为管道流量，m3/s。海森-威廉公式是在D＜1.8m 工业管道的大量测试数据基础上建立的经验公式，适用范围为部分紊流过渡区，Ch的取值范围介于100 ～157 之间［9-10］，该式在我国市政给排水管网设计中应用较广。

2.3 谢才公式

式中：C 为谢才系数，m1/2/s；R 为水力半径，m。谢才系数C 通常采用曼宁（Manning）公式计算：

式中：n 为曼宁糙率系数。曼宁经验公式最初来源于明渠均匀流的水力计算，用于管道时仅适用于紊流粗糙区或非满管重力流输水。然而，由于一直以来的工程设计习惯，以及公式简单的指数关系，我国水利工程中普遍使用该式进行水力计算，即使管内水流处于紊流过渡区流态［11］。

上述各摩阻系数之间可相互进行换算，其关系式为：

3 水力摩阻系数的敏感性分析

以达西-魏斯巴哈公式和柯尔勃洛克-怀特公式为水力计算标准，依据各摩阻系数间换算关系式（7）和式（8），分析管道内壁当量粗糙度k、管径D、流速V、水温（水流黏滞系数ν）等因素对摩阻系数取值的敏感性影响。

3.1 摩阻系数的相对变化率关系式上述各水力计算公式可写为水力坡降J 与摩阻系数、管径D 和流速V 的关系式，对水力坡降J 求全微分可得：

式中：J 为水力坡降，J= hf/L；由微分运算性质可知式（9）—式（11）表示水力坡降J 与各水力摩阻系数、流速V 和管径D 之间的相对变化率关系。特别地，当流速V 和管径D 一定时各摩阻系数的相对变化率近似满足：

上式表明：流速V 和管径D 一定时，管道内壁越粗糙，水力坡降J、达西摩阻系数λ和曼宁糙率系数n 越大，而海森-威廉系数Ch越小；曼宁糙率系数n 和海森-威廉系数Ch取值的1%相对误差将引起水力坡降J 或沿程水头损失约2%的相对误差，计算误差被成倍放大，这也进一步说明了摩阻系数合理取值对输水工程精确水力计算的重要性。

3.2 当量粗糙度k图1为DN1000mm，水温15 ℃，流速范围0.3 ～3.0 m/s（考虑工程运行的技术经济性，输水管道流速通常不超过3.0m/s［1］），当量粗糙度k 分别为0.00、0.10、0.20 和0.30 mm 时各摩阻系数随流速的变化，表1为流速V=1.0 m/s 和V=3.0 m/s 的摩阻系数值及其相对变率。由图表可知：流速V 和管径D 一定时，管道的当量粗糙度k 增大，相对粗糙度（k/D）增大，水力坡降J、达西摩阻系数λ和曼宁糙率n 值增大，海森-威廉系数Ch减小，摩阻系数间的相对变化率关系近似遵循式（12）；各摩阻系数的相对变化率随流速的增大而增大，随当量粗糙度k 的增大而减小。

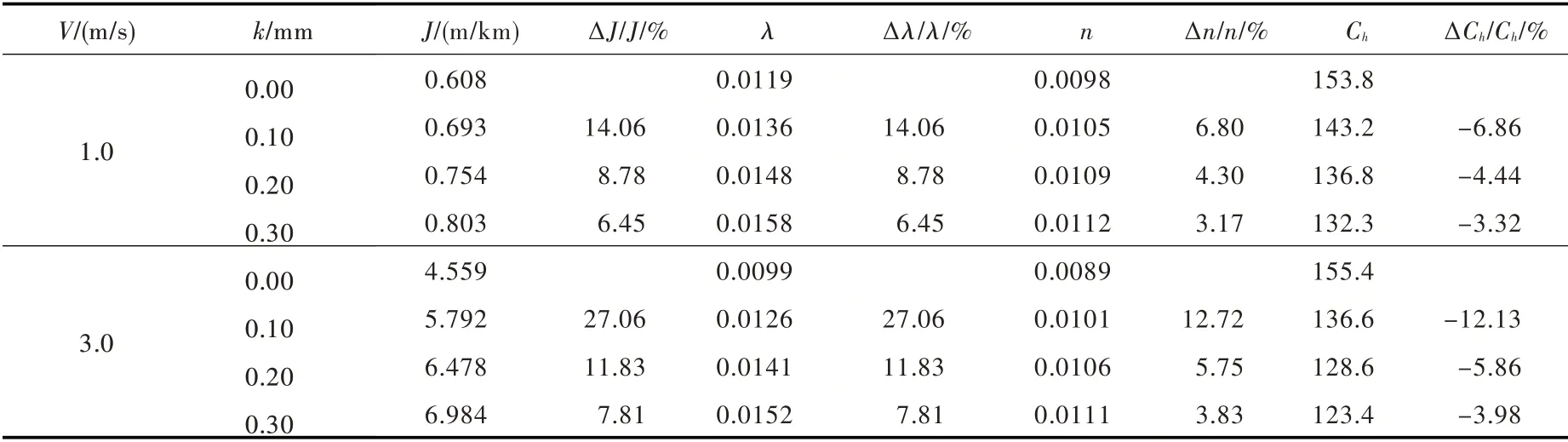
表1 当量粗糙度k 对摩阻系数的敏感性影响

3.3 管径D图2为当量粗糙度k=0.10 mm，流速范围0.3 ～3.0 m/s，DN100 ～DN2600 不同管径的摩阻系数计算结果。大量试验研究和现场检测结果表明，水泥砂浆内衬球墨铸铁管［12-13］和PCCP 管道［14-15］的当量粗糙度近似为k=0.10 mm。由图可知，当量粗糙度k 一定时，在相同流速V 和水温下，管径D增加，相对粗糙度（k/D）减小，水力坡降J 和达西摩阻系数λ减小，而曼宁糙率系数n 和海森-威廉系数Ch均增加。

曼宁糙率n 随管径D 的变化规律与《SL 702-2015 预应力钢筒混凝土管道技术规范》［16］中“同种管材，管径D 越大，粗糙系数n 越小”的论述相矛盾。由微分关系式（11）可知，水力坡降J 随着曼宁糙率n 和流速V 的增大而增大，但随着管径D 的增大而减小。由于管径D 变化引起的曼宁糙率n 的相对变化率要远小于D 的相对变化率（参见表2），因此，虽然曼宁糙率n 随着管径D 增大而略有增大，但是水力坡降J 总是随着管径D 的增大而减小。只有当管径D 一定时，水力坡降J 才随着曼宁糙率n 的增大而增大。显然，规范［16］对曼宁糙率n 与管径D 之间的变化规律考虑不足。

图3为当量粗糙度k=0.10 mm，不同流速、不同管径的曼宁糙率系数n 和海森-威廉系数Ch。由图可知：流速V=1.0 m/s 时，管径由DN100 变化到DN2600，曼宁糙率系数n 从0.0092 增大到0.0112，增幅为22%；海森-威廉系数Ch从134 增大到145，增幅为8%；管径D 对曼宁糙率n 的敏感性影响大于对海森-威廉系数Ch的影响，尤其是当D＞1.0 m 时，n 的增幅为7%，而Ch的增幅仅为1%。工程设计阶段，若不考虑管径D 的影响，对所有管径的曼宁糙率系数n 和海森-威廉系数Ch取固定值，则根据摩阻系数间的相对变化率关系式（12），沿程水头损失计算误差最大可分别达到44%（谢才-曼宁公式）和16%（海森-威廉公式）。

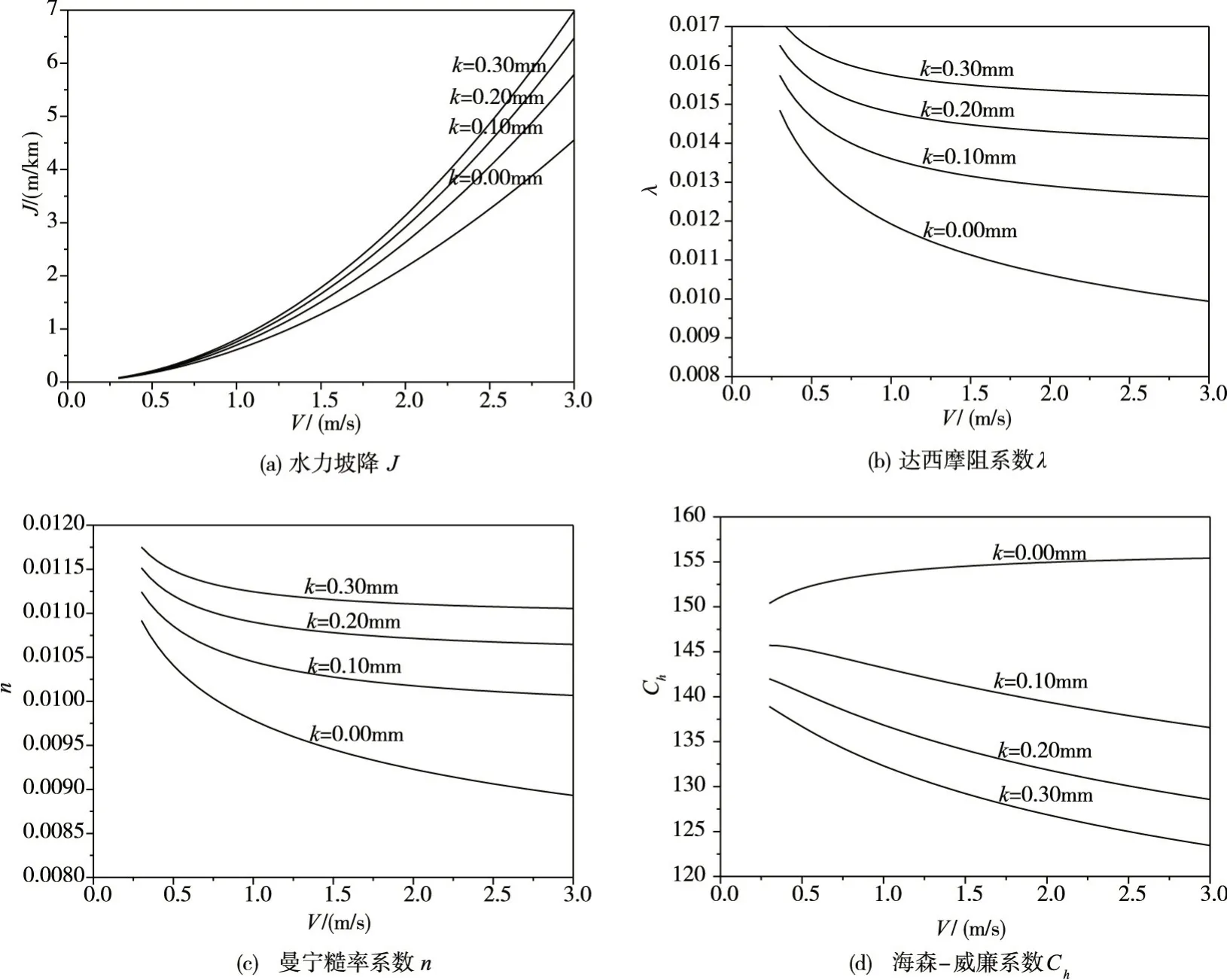
图1 当量粗糙度k 对摩阻系数的敏感性影响

表2 管径D 对水力坡降J 和曼宁糙率n 的敏感性影响

3.4 流速V如图2所示，管内水流处于紊流过渡区时，管道流速V（或流量Q）增大，相同管径D 和水温下的雷诺数Re 增大，相对粗糙度（k/D）一定时，水力坡降J 增大，达西摩阻系数λ和曼宁糙率n 减小，海森-威廉系数Ch则先增大后减小。如图3，流速从1.0 m/s 增大到2.0 m/s，曼宁糙率系数n 减小约2.71%，海森-威廉系数Ch减小约2.56%。当水流进入紊流粗糙区后，达西摩阻系数λ仅与管道的相对粗糙度（k/D）有关，此时达西摩阻系数λ和曼宁糙率n 为一常数。

3.5 水温T（运动黏滞系数ν）表3为DN1000 mm，当量粗糙度k=0.10 mm，水温分别为10 ℃（ν=1.310×10-6m2/s）、15℃（ν=1.145×10-6m2/s）、20℃（ν=1.009×10-6m2/s），流速V=1.0 m/s 和V=3.0 m/s 时各摩阻系数值及其相对变率。由表可知，管道相对粗糙度（k/D）一定时，相同流速V 和管径D，温度T 升高，运动黏滞系数ν减小，水流雷诺数Re 增大，水力坡降J、达西摩阻系数λ和曼宁糙率n 均减小，海森-威廉系数Ch增大，各摩阻系数的相对变化率关系近似满足式（12），其相对变化幅值随流速V 增大而减小。

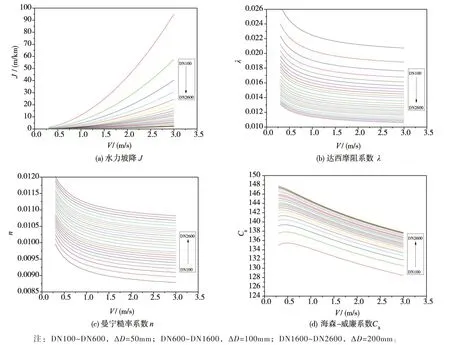
图2 管径D 对摩阻系数的敏感性影响

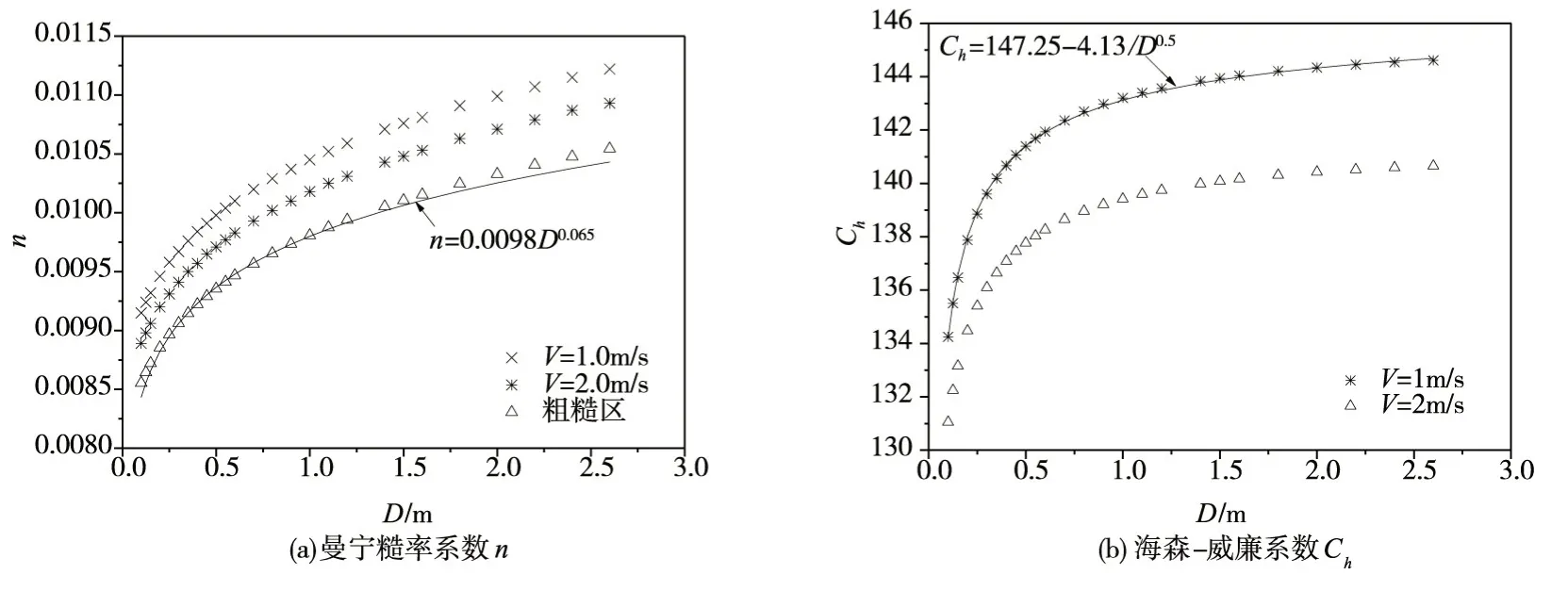
图3 管径D 和流速V 对摩阻系数的敏感性影响

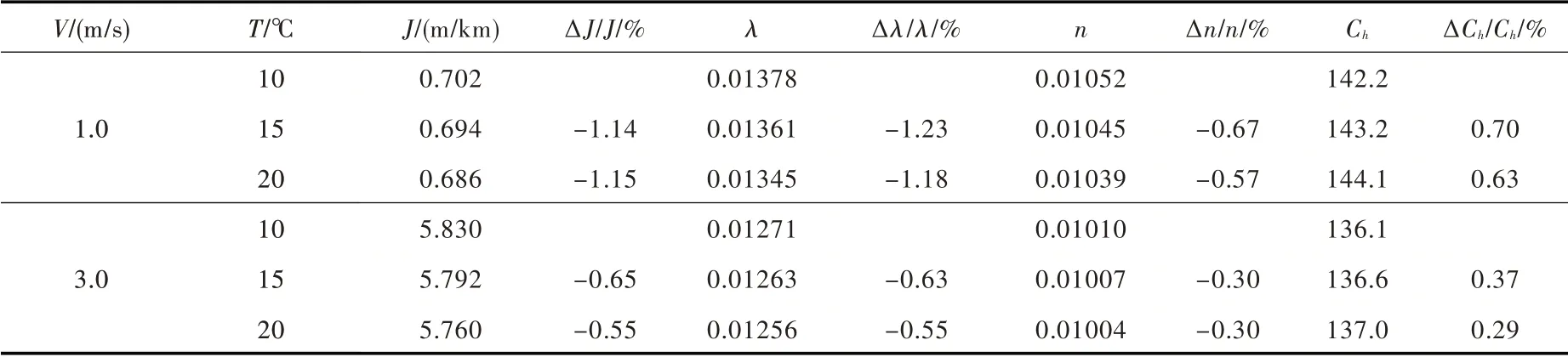
表3 水温T 对摩阻系数的敏感性影响

3.6 摩阻系数的敏感性变化规律基于柯尔勃洛克-怀特公式和各摩阻系数间换算关系，得出管道摩阻系数随当量粗糙度k、管径D、流速V 和水温T 的敏感性变化规律，如表4。对于同种管材（假定其当量粗糙度k 为一定值），管径D 的取值变化范围最大，其对摩阻系数的敏感性影响也最大，其次为流速V 的影响，水温T 的影响最小。

表4 摩阻系数随各敏感性因素的变化规律

4 实例分析与工程应用

4.1 实例分析表5为典型工程曼宁糙率系数n 和海森-威廉系数Ch的取值比较，表中实测值为工程现场测量值，设计值为工程设计取值，理论值为采用柯尔勃洛克-怀特公式求得达西摩阻系数λ后依据摩阻系数间关系式（7）和式（8）换算得到。由表可知：现有工程设计中曼宁糙率n 取值的随意性较大，考虑管径D 和流速V 影响的理论计算n 值与实测值接近，计算精度有较大地提高；海森-威廉系数Ch的经验取值较为成熟，海森-威廉公式比谢才-曼宁公式更适宜于管道输水工程的水力计算。

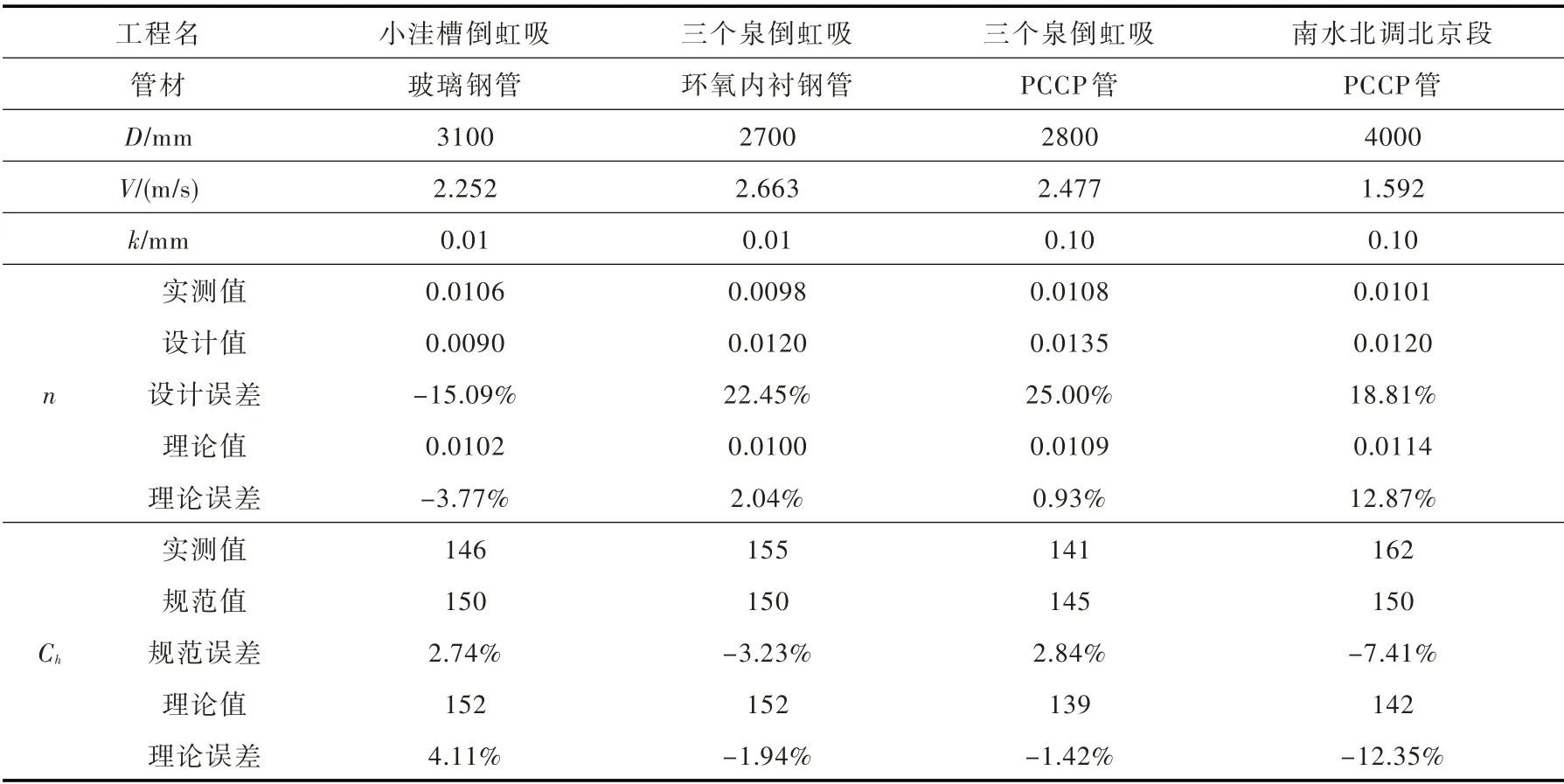
表5 典型工程案例分析［5-7］

4.2 水力计算公式的选用对于不同管材、不同管径的水力计算应优先采用达西-魏斯巴哈公式和柯尔勃洛克-怀特公式，这也是国内外规范推荐的主要公式，其计算精度较高，适用于紊流的所有流态，并在科学研究和工程实践中得到广泛验证。

海森-威廉公式适用于常温下清水输送管道的紊流过渡区，计算较为简便快捷，计算精度可满足工程要求。海森-威廉系数Ch的取值需考虑管径D 的影响，美国水行业协会（AWWA）技术手册《M9 混凝土压力管》［17］给出Ch=139.3+6.65D，《M11 钢管》［18］给出Ch=130.0+ 6.30D。图3（b）表明管径D 大于1.0 m 后，海森-威廉系数Ch随管径D 的变化趋于平缓，若采用上述规范给出的线性拟合公式，其误差将随着管径D 的增大而增大。对于k=0.10 mm、V=1.0 m/s 的水泥砂浆内衬管道其经验拟合关系式为Ch=147.25-4.13/D0.5。

随着制管工艺和水平的发展，现有大型输水工程的管道内壁均匀、光滑，水流多处于紊流过渡区，流态超出谢才-曼宁公式的适用范围，并且现有规范规定的曼宁糙率n 取值范围较宽，如规范［16］指出立式震捣法制造的PCCP 管的曼宁糙率系数n 取0.010 ～0.0125，变幅为25%，相应水头损失的变幅将达到50%。由于未考虑管径D 和流速V 的影响，造成实际工程中n 的精确取值困难，甚至较大的水头损失计算误差。

4.3 摩阻系数取值的裕度管道摩阻系数的取值不仅要考虑内壁绝对粗糙度的影响，而且需要考虑弯管、接头、阀门等的局部水头损失影响，以及长期运行后由于化学和生物作用产生的腐蚀、沉淀、结垢等对管壁粗糙度的影响［19］。实践中需综合考虑上述因素，结合工程经验，对摩阻系数的选取预留适当的裕度，以保证输水工程在长期运行过程能够达到设计流量［20］。考虑裕度的摩阻系数取值可参考关系式（12），假设工程设计中管线的水头损失预留10%的裕度，则达西摩阻系数λ需增大约10%，曼宁糙率n 需增大约5%，海森-威廉系数Ch需减小约5.4%。

5 结论

随着经济和社会发展，大口径、新材料管道在水利工程中得到广泛应用，本文对影响管道输水能力的关键参数——水力摩阻系数进行了系统的敏感性分析，得出如下结论：

（1）管道水力计算应优先采用达西-魏斯巴哈公式和柯尔勃洛克-怀特公式，尽管后者为隐式方程，需迭代求解，但在当前计算机技术发展的条件下，这不应成为该公式在工程中普遍使用的障碍。

（2）海森-威廉公式和曼宁公式均为经验公式，由于误差传递，海森-威廉系数Ch和曼宁糙率系数n 的取值误差将引起沿程水头损失计算误差的成倍放大，因此，二者的合理选取非常重要。海森-威廉系数Ch和曼宁糙率系数n 的经验取值不仅要考虑管道内壁粗糙度的影响，流速V 和管径D 的影响也不能忽略，对于同种管材，二者均随管径D 增大而增大，随流速V 增大而减小。相比较而言，海森-威廉系数Ch对不同管径D 的适应性优于曼宁糙率系数n，例如当管径D＞1.0m 时，n 的变幅为7%，而Ch的变幅仅为1%。

（3）工程设计应慎用谢才-曼宁公式。现有规范给出的曼宁糙率系数n 取值通常不考虑管径D 和流速V 的影响，且取值范围较宽，n 的精确取值困难，甚至可能影响工程效率和效益的发挥。