基于核函数的改进k-means文本聚类

张国锋 吴国文

(东华大学计算机科学与技术学院 上海 200050)

0 引 言

在计算机技术全面发展的当代，人工智能在生活当中的作用越来越重要，应用的范围也十分广泛，各行各业都对人工智能进行了大量的钻研。人们都希望在有限的时间内做足够多的事，这其中就包括阅读。就像在图书馆中阅读一样，人们在手机以及计算机上查阅资料或者阅读文章时，希望能够大大减少寻找同类型文章的时间，希望这些文章能够存放在一起而不是错综复杂的排列。但如果人工对文章进行分类需要花费大量的时间和精力，因此，让计算机来为人们提供最便捷的服务是大势所趋，机器学习中的聚类算法就得到了用武之地。

聚类算法属于“无监督学习”，而且是其中被人们研究、使用最多的算法。在聚类分析之前，每一个数据或样本属性的归类是不确定的，属性能被分成多少类一般也是需要预测的，只能依靠元数据进行分析，不像分类算法可以参考相关类别的信息。聚类分析方法主要在探索研究方面应用较多，最终的结果可能包含多种有价值的答案，如何进行筛选要依靠研究人员的实际需求和具体分析。无论实际数据能否真地被分成不同种类，使用聚类分析都可以将数据划分成特定数量的类别。聚类可以单独使用来获取数据的具体分布情况，通过研究聚类出的各个簇中数据的特征，找出特征显著的簇进行更加具体详细的分析。

1 文本预处理

若要对文章进行聚类，需要对文章进行一定的处理，这些操作包括对文章进行分词、去除停用词、使用TF-IDF找出每篇文章的关键词以及使用Word2Vec将关键词向量化。

1.1 分词处理

首先使用jieba算法对文章进行分词。jieba分词有三种模式：精确模式、全模式以及搜索引擎模式。这里使用精确模式，此模式的目的是把语句最精确地切分开，适用于文本分析，分词之后的文本存入txt文件中。

其次需要去除停用词。分词之后的文本现在以若干词语集合的形式呈现。其中很多字词并没有实际的意义，例如“的”、“是”等，这些词会影响之后提取关键字的准确性，因此需要把这些没有实际意义的字词除去。由此构造了一个停用词字典，对词语集合进行筛选，若集合中的字词出现在停用词字典中，则删除。

1.2 特征选取

本文使用TF-IDF算法找出文本中的关键词，将权值最大的20个关键词作为特征代表文本进行聚类。TF-IDF的原理可以通俗易懂的解释为：如果一个词语或者短语在某篇文章中以很高的频率出现，然而在其他的文章中几乎没有，那么就认为这个词语或者短语具有良好的代表性，适合用来做区分。具体计算公式如下：

(1)

式中：i代表文本中的词语；Ti表示该词语出现的次数；Nt表示文章的总词数；Dn表示文本总数；Dt表示包含词语i的文本数。

返回的结果是一个列表和一个矩阵。列表中存放的是所有文本的词语汇总，每个词语只存储一次。矩阵每行存储的是每个词语在一个文本中的权值数据，排列顺序与列表中词语的排列顺序一致，若某个词并未出现在某个文本中，则权值为0。

1.3 文本向量化

最后的处理工作是把文本向量化。把分词后的所有文本当作语料库，使用Word2Vec模型进行词向量化。Word2Vec根据词义把词语映射到距离接近的空间中，词向量能够表达出一定的语义信息。此次选择CBOW训练模式，这种模式通过前后文预测目标词。属性windows意思是目标词与预测词的距离，此次大小设为5，通过目标词前后文共10个词得到当前词的向量，维度size设定为20。在得到的向量库中匹配出各个特征的向量Vi，将特征向量相加得到最终的文本向量Vd：

(2)

这样就可以使用向量Vd来进行聚类工作。

2 相似度定义

本文使用高斯核函数计算文本之间的相似度。高斯核函数的公式如下：

(3)

一种等价且更为简单的定义公式为：

(4)

式中：γ=1/2σ2。

高斯核函数对于数据中的噪音有着很不错的抗干扰能力，函数中的σ参数决定了函数的有效区域，超过了此范围，数据的影响就会基本忽略。由于噪音对k-means算法的影响很大，所以使用高斯核函数来降低噪音的影响。此外，高斯核函数能够利用高维空间向量之间的内积得出两个点之间的距离，降低了计算难度。

高斯核函数对自身的参数σ比较敏感，本次实验通过交叉验证法确定参数σ。使用距离协方差作为参数，因为协方差能很好地反映各维数据的离散状况，很符合核函数参数的性质。协方差公式如下：

(5)

其中:n代表数据的总数；xi为第i个具体的数据。

从原始数据中随机选择400个数据，平均分为4组，其中三组记为A、B、C，当作训练集，最后一组记为D，作为最终的验证集，用验证集来选出最合适的一个当作参数。

具体做法是：使用传统k-means算法对三个训练集进行聚类，使用欧氏距离作为距离公式，k值定为3。每组聚类后会有3个簇，把各簇误差的协方差(精确到小数点后五位)分别记为s1、s2、s3，把它们的平均值记作S，这里的误差是指当前点到簇质心的距离。随后将它们分别代入高斯核函数中，使用测试集D的数据进行聚类。测试集使用误差平方和(SSE)来评估聚类效果，SSE的值越小，表示数据点离它们的质心越近，聚类效果也就越好。测试集每个簇的误差平方和分别用d1、d2、d3表示，从中选出平均误差平方和最小的一组，将S值作为σ。训练集具体数据如表1所示。

表1 训练集数据

测试集数据如表2所示。

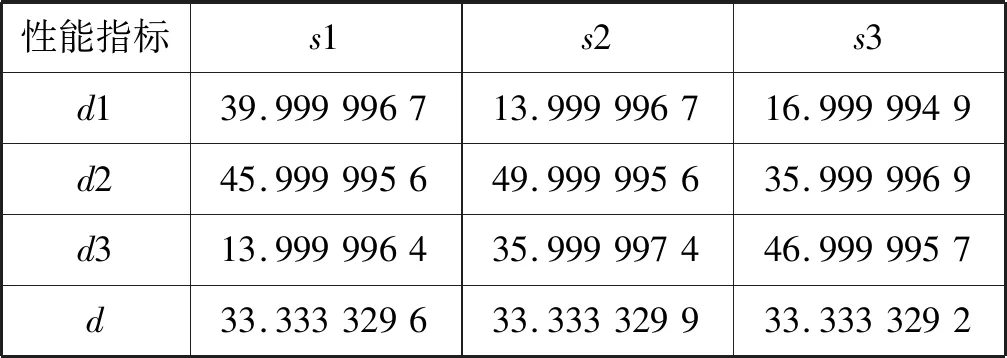
表2 测试集结果

由测试集数据可了解到，当S为0.002 17的时候，效果最好，这表明，可以确定σ取值为0.002 17。

3 k-means算法改进

3.1 传统k-means算法

k-means是划分方法中较经典的聚类算法之一。由于该算法的效率高，所以普遍应用于对大规模数据进行聚类。目前，许多算法均围绕着该算法进行扩展和改进。

k-means算法的逻辑如下：确定聚类的个数k，随机确定初始质心的坐标，选择合适的距离公式计算每个数据与每个质心的距离，并将其聚类到距离最近的簇中。在所有数据完成聚类后，更新每个簇的质心坐标并重新计算每个点与质心的距离，将数据点重新聚类到距离最近的簇中。重复以上步骤直到质心不再变化，聚类完成。

k-means算法的优点是简单、快速，当数据很密集时，效果较好。缺点是要事先确定准备生成的簇的数目k，对于初始质心坐标和噪声很敏感，不同的初始值结果可能会不一样，当k值预估过大时，可能出现空簇。

3.2 使用改进的k-means算法聚类

由于初始质心的随机性对k-means的结果影响很大，数据很可能收敛到局部最小值，并且会产生空簇，所以此次实验对传统k-means做出了改进。

用k′表示距离指定k值的差，Δk表示当前将要增加的质心数。改进后的算法先随机生成k/2个初始质心，初始k′=k-k/2。将所有数据聚类到k/2个簇中，如果有a个簇中没有数据，则直接删除这些质心并更新k′=k′+a。每次增加Δk=k′/2个质心，利用误差平方和来判断聚类过程中的效果，找出聚类过程中SSE值最大的Δk个簇分别进行k为2的局部聚类，将原先的簇划分成两个，再重新计算每个簇的SSE，重复以上步骤，直到簇的数目达到k为止。

具体步骤为：

(1) 初始化k/2个质心，质心坐标随机确定：

(6)

(2) 将所有的数据聚类到这些簇中，判断是否有空簇并记录个数a，若有即刻删除，并更新k′和Δk：

k′=k′+a

(7)

Δk=k′/2

(8)

(3) 比较每个簇的SSE值,找出值最大的Δk个簇，进行局部二分聚类。

(4) 更新k′以及Δk的值并重复第3步的操作：

k′=k′-Δk

(9)

(5) 当簇的数量达到k即k′为0时，聚类结束。

经过这一改进后，可以有效降低SSE的值，使数据最大化地收敛到全局最小值，还可以避免出现空簇，改善了有效簇未达到期望值的缺陷。

4 结果分析

4.1 实验一

为了对比，分别使用传统k-means算法和改进后的k-means算法做了两组聚类对比实验。选取的文本字数在500到1 500字之间，具有普遍性和一般性。数据文本共选取2 000篇，分为三组，第一组300篇，第二组700篇，第三组1 000篇。

由于计算距离公式不同，所以使用平均误差平方和(AvgSSE)与最大误差平方和(MaxSSE)的比值(pSSE)作为评估标准之一，计算公式如下：

(10)

比值保留到小数点后5位。结果分别从聚类的迭代次数(t)、pSSE以及空簇的数量(Ne)进行对比。结果如表3所示。

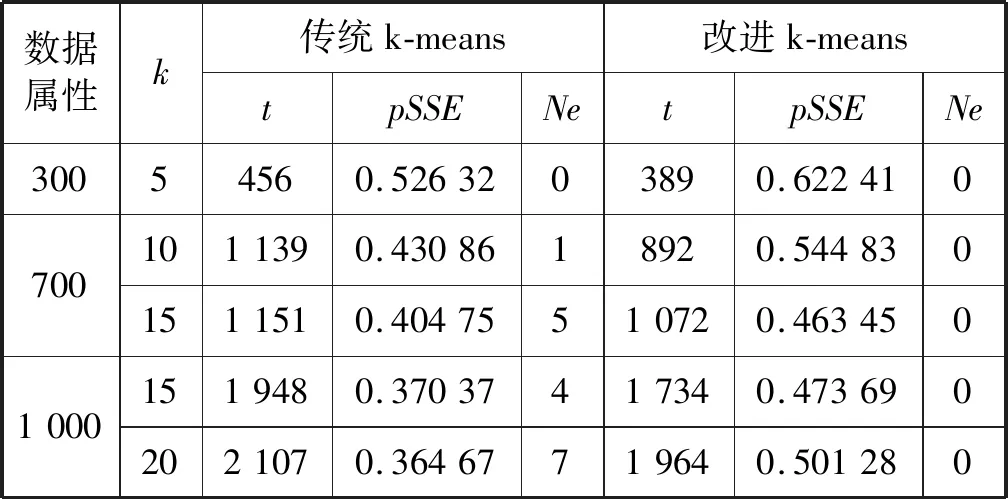
表3 实验一结果对比

由最后结果对比可知，在迭代次数上，改进后的算法较传统算法所用次数明显减少。原因有两点：第一是初始的质心只为k值的一半，基础的迭代次数必然减少；第二是因为算法后期的局部聚类相当于二分聚类，每次增长的幅度相对较小。

在pSSE方面，改进后的算法要大于传统算法。pSSE较小说明最大的误差平方和相对较大，传统的聚类方法得出的簇很可能出现某一簇的范围很大而其他簇的位置很集中，这就说明聚类效果不是很好。而改进后的算法聚类出的每个簇的数据更集中，平均每个数据距离质心更近,从而说明改进后的算法聚类效果要优于传统算法。

此外，较大数据量的两组分别聚类了两次进行对比。可以看到改进后的算法并没有出现空簇，而传统算法虽数据量没有变，但是由于初始的质心发生变化，导致出现的空簇数量不定，或多或少，随着文本的增多，出现空簇的可能性也增大。改进后的算法彻底修正了传统算法的这个缺陷，保证了聚类结果能达到数量上的基本要求。

4.2 实验二

实验二选取了金融类、汽车类、体育类、天气类以及食品类文本各100篇混合成源数据进行聚类。分别从准确率(precision)、召回率(recall)以及F值进行对比。准确率是指聚类后，各类文本数量Nt与该簇全部文本数量NT的比值。公式为：

precision=Nt/NT

(11)

召回率是指Nt占相对应类型文本Nm的比值：

recall=Nt/Nm

(12)

F值计算公式为：

(13)

实验结果如表4所示。

由实验二数据可以看出，改进后的算法整体在准确率和召回率上都有了明显提升，F值也因此提高。只有食品类准确率少许降低，原因可能是食品类文本中的词语与其他类重复得过多，但召回率的提高使得F值并没有降低。由此从整体上来看，改进后算法的聚类效果比传统算法的聚类效果要好。

5 结 语

本文结合TF-IDF与Word2Vec对文本实现向量化，并针对传统k-means算法易收敛到局部最小值，对噪声敏感等不足之处做出改进，以高斯核函数作为距离公式，并在聚类过程中降低误差平方和，提升聚类效果，对文本进行了高效聚类。实验结果表明，本文算法在效果上优于传统k-means聚类，并消除了聚类结果出现空簇的可能性。