改进的频繁项集挖掘算法及其应用研究
2019-09-13顾军华李如婷张亚娟董彦琦
顾军华 李如婷 张亚娟* 董彦琦
1(河北工业大学人工智能与数据科学学院 天津 300401)2(河北省大数据计算重点实验室 天津 300401)
0 引 言
在当今大数据时代,如何从海量的数据中去粗存精,挖掘出隐藏的、有价值的信息,为各行各业的管理者提供决策支持具有十分重要的意义[1]。关联规则挖掘是数据挖掘中一个十分重要的研究方向,其主要任务是发现数据库中项集之间隐藏的关系,且广泛应用于商店营销、库存控制、农作物选择和生物信息学等多个领域[2]。关联规则挖掘主要包括挖掘频繁项集和发现强关联规则两部分,挖掘频繁项集是其中很重要的一步。因此许多用于挖掘频繁项集的算法被提出,这些算法主要分为两类:Apriori类算法和FP-growth类算法[3]。
Apriori算法最初是由Agrawal等[4]提出来的,该算法先通过自连接(k-1)-项集产生候选k-项集,然后根据最小支持度和Apriori先验定理对候选项集进行剪枝,从而获得频繁k-项集。Apriori算法简单且易于理解,但是面对庞大的数据时,该算法存在以下两个问题:(1) 产生大量的候选项集;(2) 需要重复多次扫描数据库,造成了巨大的I/O负载。与Apriori类算法不同,FP-growth算法只需要两次扫描数据库且没有候选项集生成,挖掘效率较Apriori算法有很大提升[5]。然而FP-growth算法在挖掘过程中需要频繁构建条件模式树(Frequent Pattern tree,FP-tree)和条件模式基,带来了巨大的时间和空间消耗。
利用FP-growth算法的思想,Deng等提出了PrePost算法[6],该算法通过前序和后序遍历FP-tree,构建了一棵基于前序和后序编码的树(Pre-order and Post-order Code tree,PPC-tree),从中得到1-项集的N-list,然后通过迭代连接两个项集的N-list得到新的项集,减少了时间和空间的消耗。但PPC-tree的构建需要两次遍历树,而且在连接N-list时没有进行剪枝操作,产生了大量冗余的N-list。在此基础上,Deng等又提出了FIN算法[7],该算法提出了一种新的数据结构——Nodesets来挖掘频繁项集,Nodesets是从前缀编码树(Pre-order Code tree,POC-tree)中得到的。相比PrePost算法,FIN算法在构建POC-tree时只需要前序遍历树,建树过程简单,而且挖掘过程中使用了父子等价的剪枝策略,缩小了挖掘空间。但是在连接两个Node-sets时,需要多次遍历POC-tree,判断二者是否满足连接条件,耗费了大量的时间。为此,Aryabarzan等[8]提出了negFIN算法,该算法使用位图表示树中的节点信息,通过位运算连接两个(k-1)-项集得到k-项集,避免了多次遍历树的过程,挖掘效率较FIN算法有一定提高。但是当面对大型数据库时,位运算的过程较复杂,而且使用位图表示节点会占用大量的空间。
上述基于FP-growth思想的算法虽然提高了挖掘频繁项集的效率,但大都存在生成频繁k-项集过程复杂、耗费空间多的问题,如:FIN算法在连接Nodesets时需要多次遍历树,耗费了大量时间;negFIN算法使用位图表示节点会占用大量空间。为此,本文提出了一种基于前序完全构造链表(Pre and Finishbuilding List,PF-List)的频繁项集挖掘算法(PF-List Frequent Itemsets Mining,PFLFIM)。该算法在POC-tree的基础上,增加了节点在树中被完全构造的顺序编号(Finishbuilding-order),形成了一棵基于前序和完全构造顺序编码的树(Pre-order and Finishbuilding-order Coding tree,PFC-tree),从中得到1-项集的PF-List,然后通过迭代连接(k-1)-项集的PF-List得到k-项集。在连接过程中,PFLFIM算法通过简单比较两个PF-List的pre-order和finishbuilding-order编号进行连接,避免了复杂的连接运算。此外,该算法用模式搜索树表示搜索空间,并使用包含索引、提前停止交集和父子等价策略对搜索树进行剪枝,减少了空间占用,加快了挖掘速度。在Pumsb和Retail数据集上进行实验,结果表明,PFLFIM算法在运行时间和空间占用上均优于FIN算法和negFIN算法。最后,利用PFLFIM算法对某高校人才数据进行关联规则挖掘,从中提取隐含的且有价值的信息,并运用它们寻找影响人才发展的因素,为高校人才引进和选拔提供决策支持。
1 相关概念
1.1 基本概念
给定一个事务数据库DB,如表1所示。设集合I={i1,i2,…,in}是数据库中所有项的集合,集合T={T1,T2,…,Tm}是数据库中所有事务的集合,且|DB|=m。每个事务Ti都是I的子集,即∀Ti∈T,∃Ti⊆I。
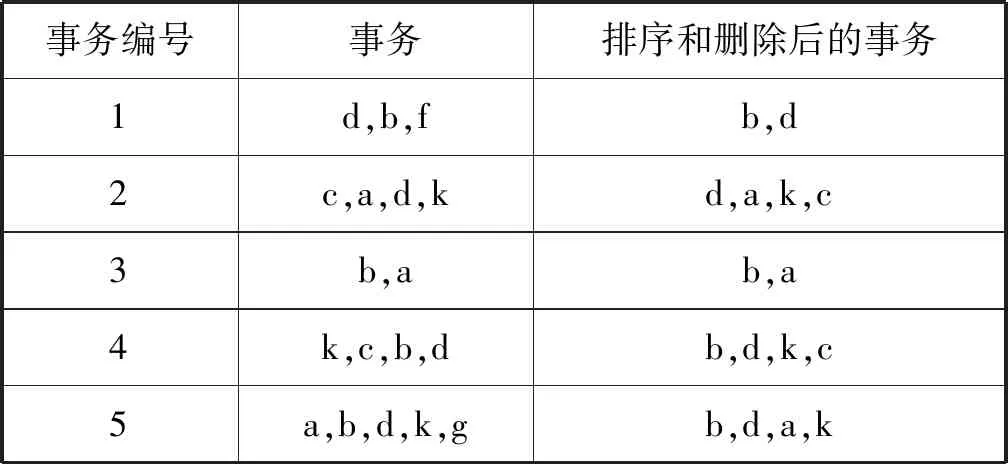
表1 事务数据库DB
定义1设集合X={x1,x2,…,xk}是I的子集,即X⊆I,则称X为I中的项集。如果项集X包含k个项,则称X为k-项集。把包含项集X的事务数称为X的支持度计数,记为support_count(X),把X的支持度计数与事务总数之比称为X的支持度,记为support(X),其计算式表示为:
(1)
定义2给定一个最小支持度minSup(取值范围为[0,1]),若support(X)≥minSup,则X是频繁的,若X的长度为k,则称X为频繁k-项集。
由定义1可得表1所示数据库的1-项集及其支持度计数,如表2所示。设minSup为0.4,由定义2可得频繁1-项集为{a}、{b}、{c}、{d}、{k}。将每个事务中不频繁的项删除,然后按项的支持度计数降序排列后的事务如表2所示。

表2 1-项集及其支持度计数
定义3关联规则是形如X→Y的表达式,且X∩Y=∅,它的强度可以用置信度衡量。置信度表示项集Y在包含X的事务中出现的频繁程度,记为confidence(X→Y),其计算式表示为:
(2)
式中:support(X∪Y)表示同时包含X和Y的事务数在事务数据库中所占的比例,support_count(X∪Y)表示同时包含X和Y的事务数。给定一个最小置信度minConf(取值范围为[0,1]),若confidence(X→Y)≥minConf,则称X→Y是强关联规则。
性质1对于给定的事务数据库DB,设定最小支持度和最小置信度,关联规则挖掘是指查找数据库中支持度不小于最小支持度且置信度不小于最小置信度的所有强关联规则。
1.2 PFC-tree
PFC-tree是由一个空的root节点和前缀子树构成的,树中的节点由item-name、count、child-list、pre-order和finishbuilding-order等五部分构成。item-name存储节点代表的项,count存储从root到此节点的路径表示的项集所匹配的事务数,child-list存储节点的所有子节点,pre-order表示前序遍历PFC-tree时节点的顺序编号,finishbuilding-order表示节点在PFC-tree中被完全构造的顺序编号。
遍历一次数据库就可以得到PFC-tree中各节点的item-name、count、child-list和finishbuilding-order信息,然后前序遍历PFC-tree,得到每个节点的pre-order,完成PFC-tree的构建。同POC-tree相比,节点中的finishbuilding-order是在构建PFC-tree时得到的,不用花费多余的时间。而且PFC-tree主要用于生成频繁1-项集的PF-List,在生成列表后,可以直接从内存中删除。但POC-tree在构建后仍需多次遍历,消耗了大量的内存。所以相比POC-tree,构建PFC-tree在没有耗费多余时间的基础上,还节省了空间,提高了挖掘的效率。PFC-tree的构建如算法1所示。
算法1构建PFC-tree
输入:事务数据库DB,最小支持度minSup
输出:频繁1-项集F1,PFC-tree
1: 扫描数据库DB,得到频繁1-项集F1;
2: 根据F1处理数据库中的事务;
3: 创建根节点Node,Node.item-name←root,parent←Node;
4: 初始化finish=0;
5: for each事务中的项i do
6: 创建节点N,parent.child-list←N,
N.item-name←i,
N.count←包含i的事务数;
N.finishbuilding-order←++finish;
parent←N;
7: end for
8: 遍历PFC-tree,得到每个节点的前序编号pre-order;
9: returnF1,Node;
根据算法1,构建表1所示数据库的PFC-tree,如图1所示。
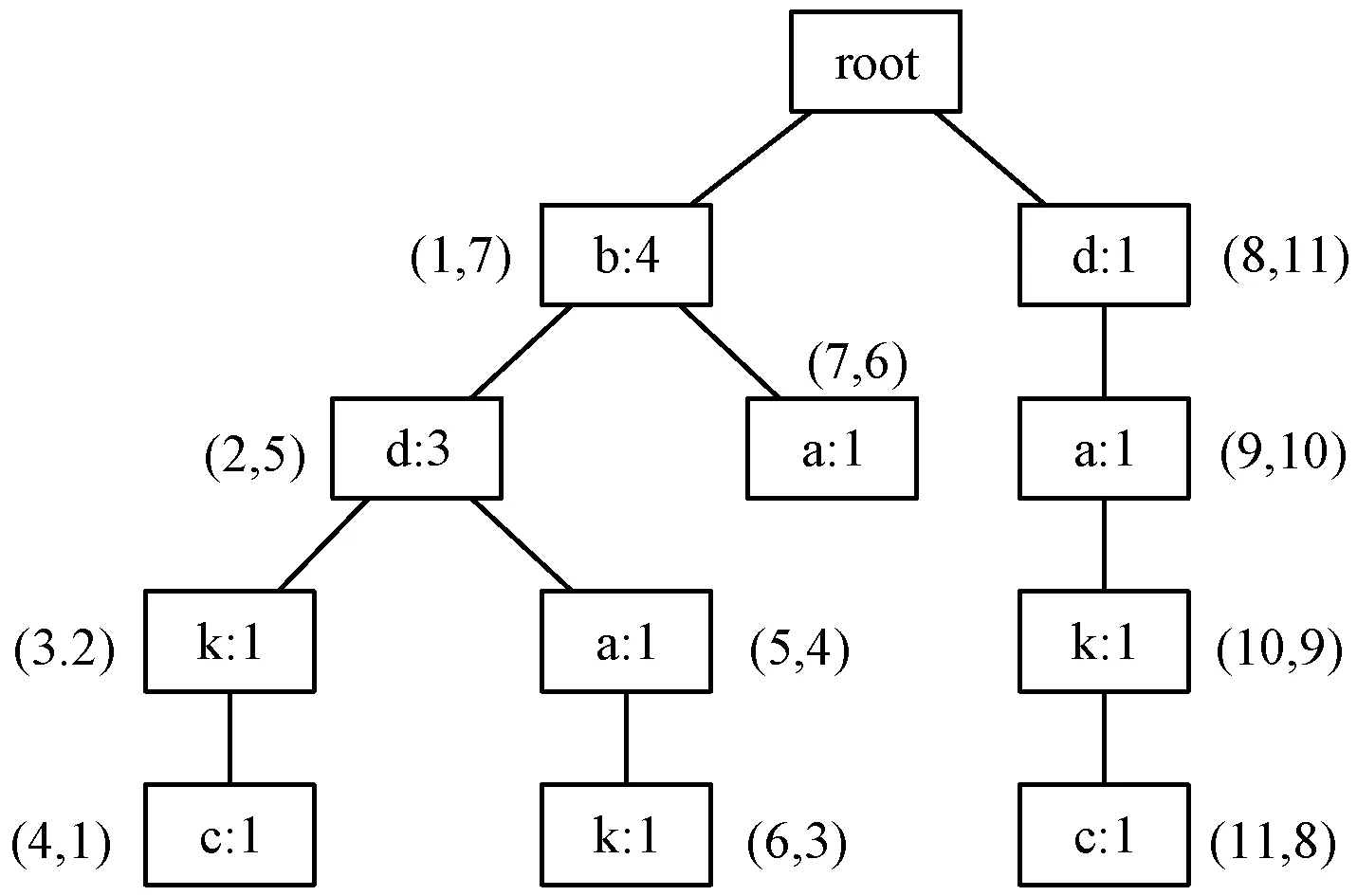
图1 事务数据库对应的PFC-tree
1.3 PF-List的概念与性质
由PFC-tree可得到频繁1-项集的PF-List,为了定义PF-List,首先给出PFC-tree中每个节点信息的定义。
定义4对于PFC-tree中的每个节点N,用<(pre-order,finishbuilding-order):count>表示N的信息,称其为节点N的PF-info。
性质2给定PFC-tree中的两个节点N1和N2,N1和N2的前序编号和完全构造编号分别为N1.pre-order、N1.finishbuilding-order和N2.pre-order、N2.finishbuilding-order。当且仅当N1.pre-order
定义5频繁1-项集的PF-List是指将所有代表项i的PF-info按照前序编号升序排列得到的列表,频繁1-项集{i}的PF-List记作PFL({i})。以图1所示的PFC-tree为例,得到的频繁1-项集的PF-List如图2所示。例如,项集{b}的PF-List,PFL({b})={<(1,7):4>}。
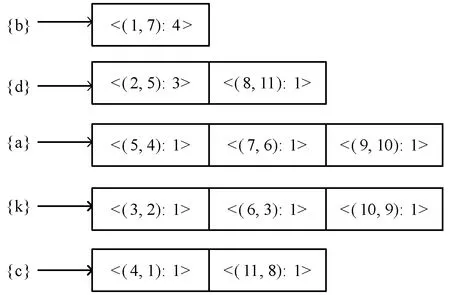
图2 频繁1-项集的PF-List
性质3若PFL(I)={<(pre1,finish1):c1>,<(pre2,finish2):c2>,…,<(pres,finishs):cs>},那么项集I的支持度计数support_count(I)=c1+c2+…+cs。
定义6假设一个2-项集{ij},其中项集{i}的支持度大于项集{j}的支持度,且PFL({i})={<(pre1i,finish1i):c1i>,<(pre2i,finish2i):c2i>,…,<(premi,finishmi):cmi>},PFL({j})={<(pre1j,finish1j):c1j>,<(pre2j,finish2j):c2j>,…,<(prenj,finishnj):cnj>},根据以下规则生成2-项集{ij}的PF-List。
(1) 根据性质2判断,如果PFL({i})中某个节点<(premi,finishmi):cmi>是PFL({j})中某个节点<(prenj,finishnj):cnj>的祖先,那么将<(premi,finishmi):cnj>加入项集{ij}的PF-List。
(2) 检查项集{ij}的PF-List,把前序编号相同的节点的count相加,合并为一个节点。
(3) 根据性质3计算出项集{ij}的支持度计数support_count({ij}),若support_count({ij})≥minSup×|DB|,则项集{ij}是频繁2-项集。
定义7频繁k-项集的PF-List是通过连接两个频繁(k-1)-项集的PF-List得到的。设频繁(k-1)-项集I1={ixi1i2…ik-2},I2={iyi1i2…ik-2},其中项集{ix}的支持度大于项集{iy}的支持度,且PFL(I1)={<(pre11,finish11):c11>,<(pre21,finish21):c21>,…,<(prem1,finishm1):cm1>,PFL(I2)={<(pre12,finish12):c12>,<(pre22,finish22):c22>,…,<(pren2,finishn2):cn2>},根据定义6中的规则生成频繁k-项集I=I1∪I2={ixiyi1i2…ik-2}。
例如:根据定义6,连接项集{b}和项集{a}的PF-List得到项集{ba}的过程如图3所示;根据定义7,连接项集{ba}和项集{da}的PF-List得到项集{bda}的过程如图4所示。
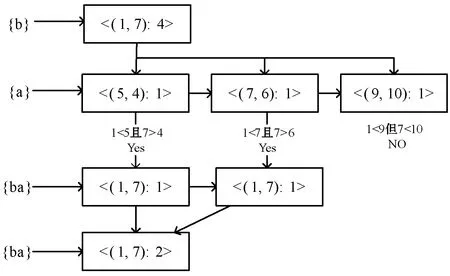
图3 1-项集的PF-List连接
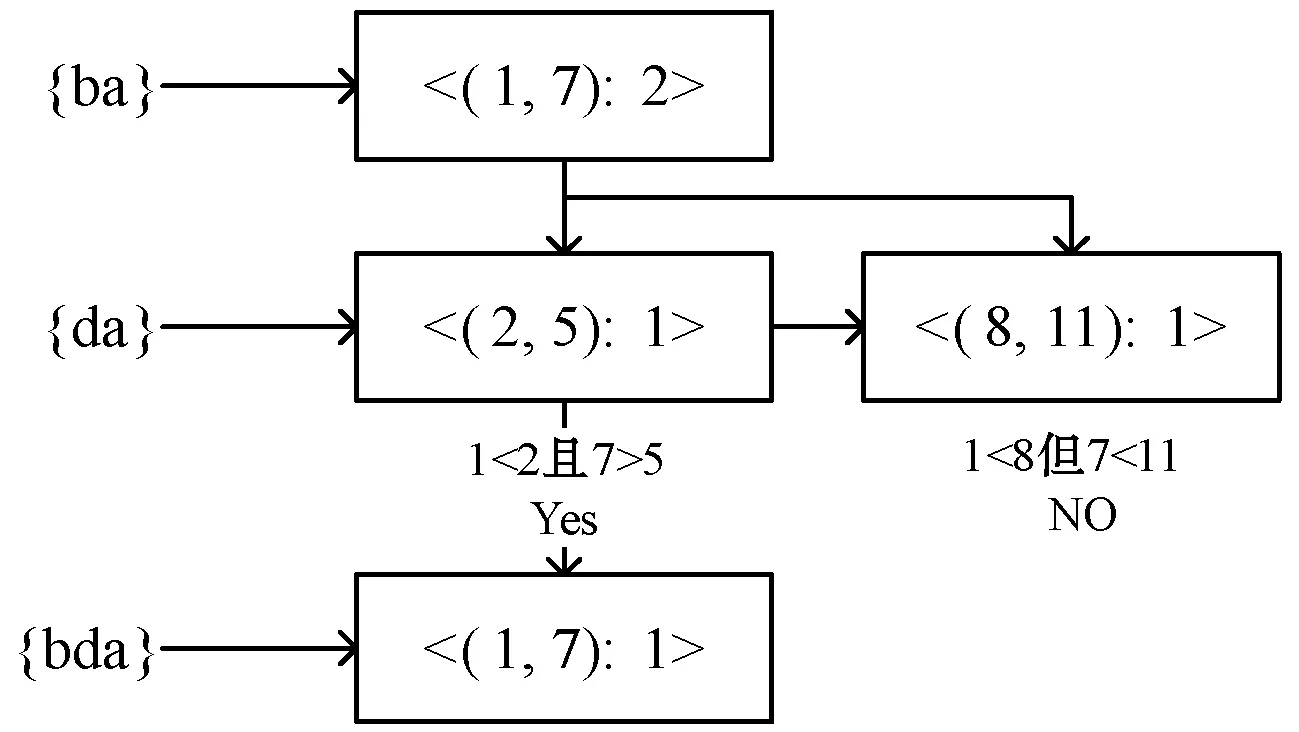
图4 k-项集的PF-List连接
2 基于PF-List的频繁项集挖掘算法
PFLFIM算法使用PF-List表示项集,通过简单比较两个PF-List的节点信息,判断其是否满足连接条件,若满足则连接得到新的PF-List,从中得到频繁项集及其支持度,连接过程较FIN算法和negFIN算法简单,降低了时间复杂度。在挖掘频繁项集的过程中,为了避免重复连接,PFLFIM算法用模式搜索树代表搜索空间。在搜索过程中,使用了包含索引、提前停止交集和父子等价策略对搜索空间进行剪枝,缩小了算法的搜索空间,提高了挖掘效率。
2.1 频繁项集挖掘
2.1.1模式搜索树
在挖掘频繁k-项集时,为了避免重复连接,PFLFIM算法使用模式搜索树来代表搜索空间。模式搜索树是根据事务数据库中的项按照某全序关系≤L生成的[10]。对于表1中的事务数据库DB,所有频繁1-项集组成的项集F={b,d,a,k,c},规定全序关系为将F中的项按照支持度计数降序进行排列,即b≤Ld≤La≤Lk≤Lc,则表1所示数据库的模式搜索树如图5所示。树的根节点为空集,其余节点都是F的非空子集,假定树的最上层为第0层,层数依次递增,每层都包含与该层层数一致的项集,那么通过遍历树的第k层就可以得到所有的k-项集。
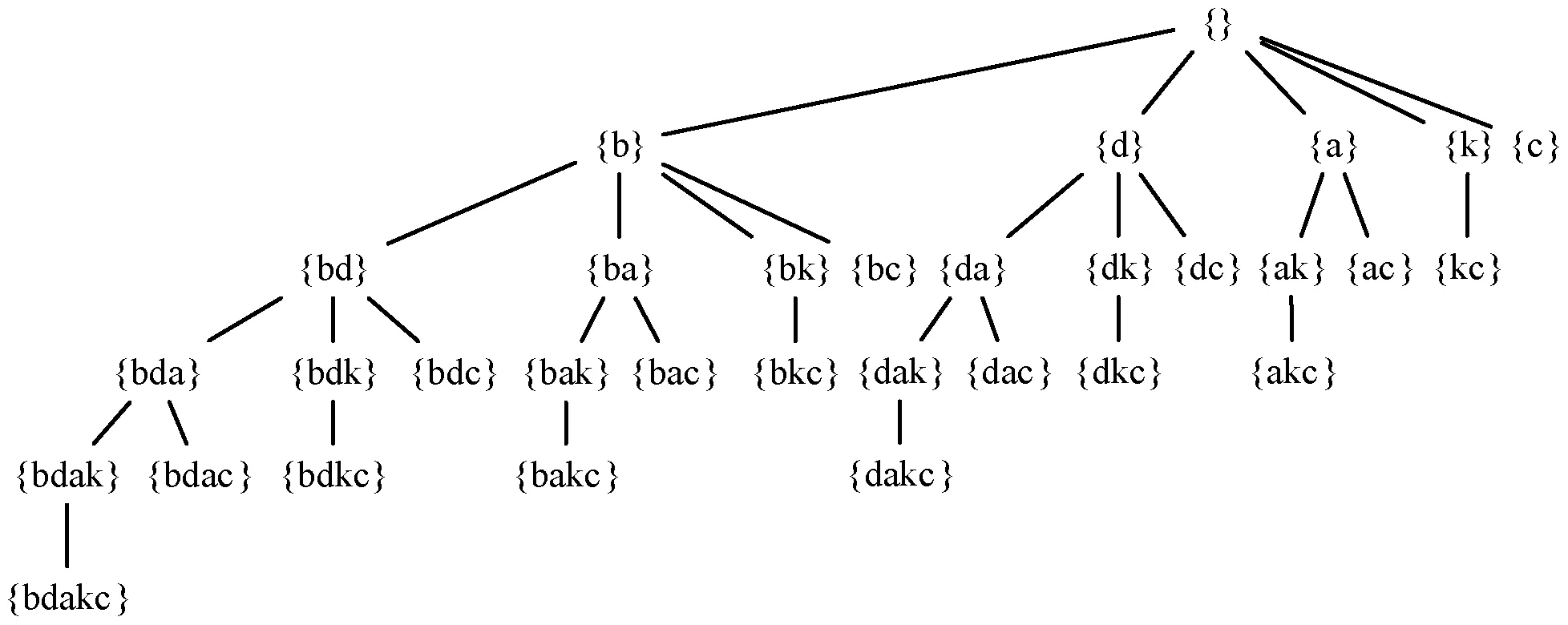
图5 数据库DB的模式搜索树
2.1.2优化策略
遍历模式搜索树时,使用包含索引、提前停止交集和父子等价策略对模式搜索树进行剪枝操作,从而减小了搜索空间。
包含索引是一门用于减少频繁模式挖掘搜索空间的技术[9]。1-项集{i}的包含索引subsume({i})的定义表示为:
subsume({i})={j∈I|∀Ni∈PFL(i),∃Nj∈PFL(j)∧
Nj是Ni的祖先}
(3)
式中:Ni表示项集{i}的PF-List中的某个节点,Nj表示项集{j}的PF-List中的某个节点。若项集{i}的PF-List中的任何一个节点Ni,都可以在项集{j}的PF-List中找到一个祖先节点Nj,那么项集{j}就是项集{i}的包含索引。例如,从表1所示数据库得到的1-项集及其包含索引如表3所示。
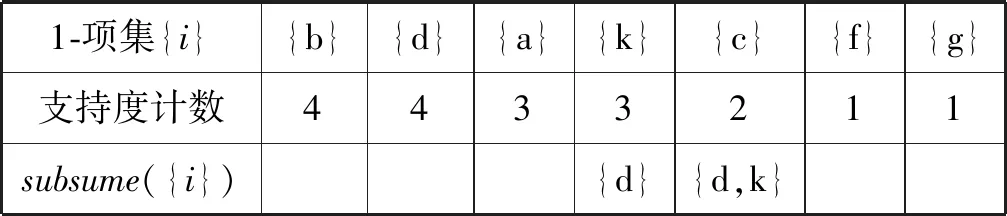
表3 1-项集和对应的包含索引
性质4若存在一个项集F,且F的包含索引subsume(F)={f1,f2,…,fs},那么F与{f1,f2,…,fs}中任何一个非空子集求并集得到的项集的支持度都等于F的支持度,其计算式表示为:
support(F)=support(F∪J)|∀J⊂subsume(F)
(4)
例如,表3中项集{k}的包含索引subsume({k})={d},根据性质4可知,support({dk})=support({k})=3。在挖掘频繁项集时,使用包含索引策略,可以直接得到一些频繁项集及其支持度,节省了执行连接操作的时间,提高了算法的运行速度。
性质5提前停止交集剪枝策略[11]。设有两个频繁(k-1)-项集I1和I2,使用提前停止交集策略连接I1和I2的PF-List的具体步骤如下所示:
(1) 根据性质2,计算项集I1和I2的PF-List的总计数,分别记为C1和C2。
(2) 依次取两个PF-List中的每个节点N,判断与另一个PF-List中的节点是否存在祖先-后代的关系。如果不存在,若N∈PFL(I1),则C1=C1-N.count,若N∈PFL(I2),则C2=C2-N.count。
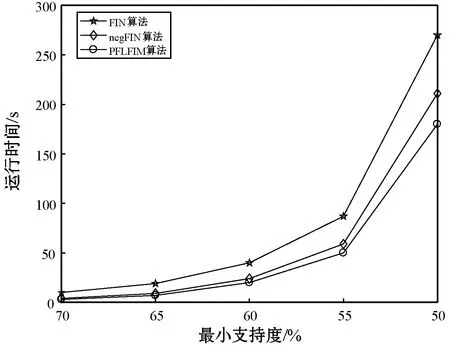
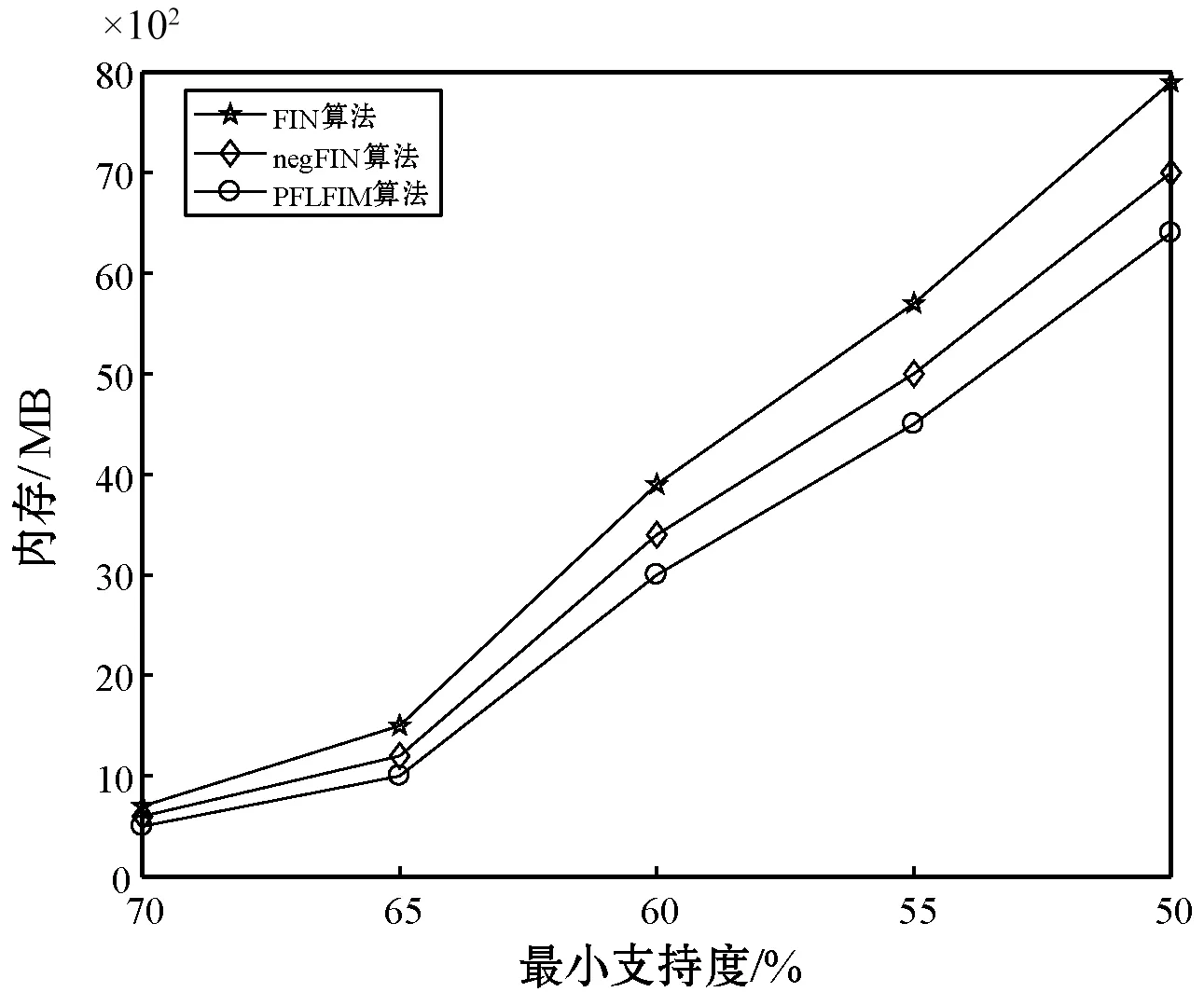
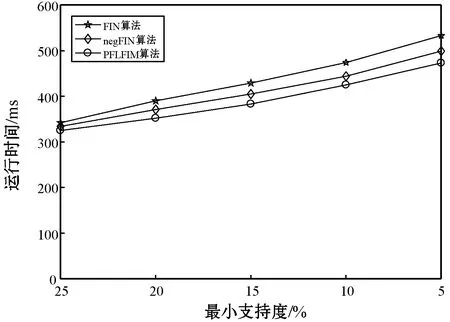
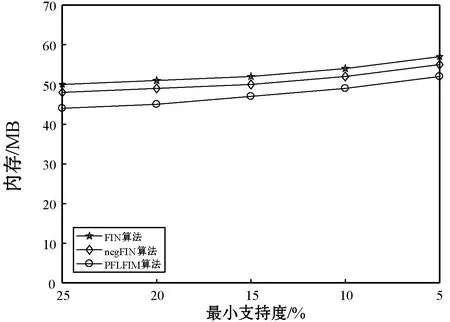
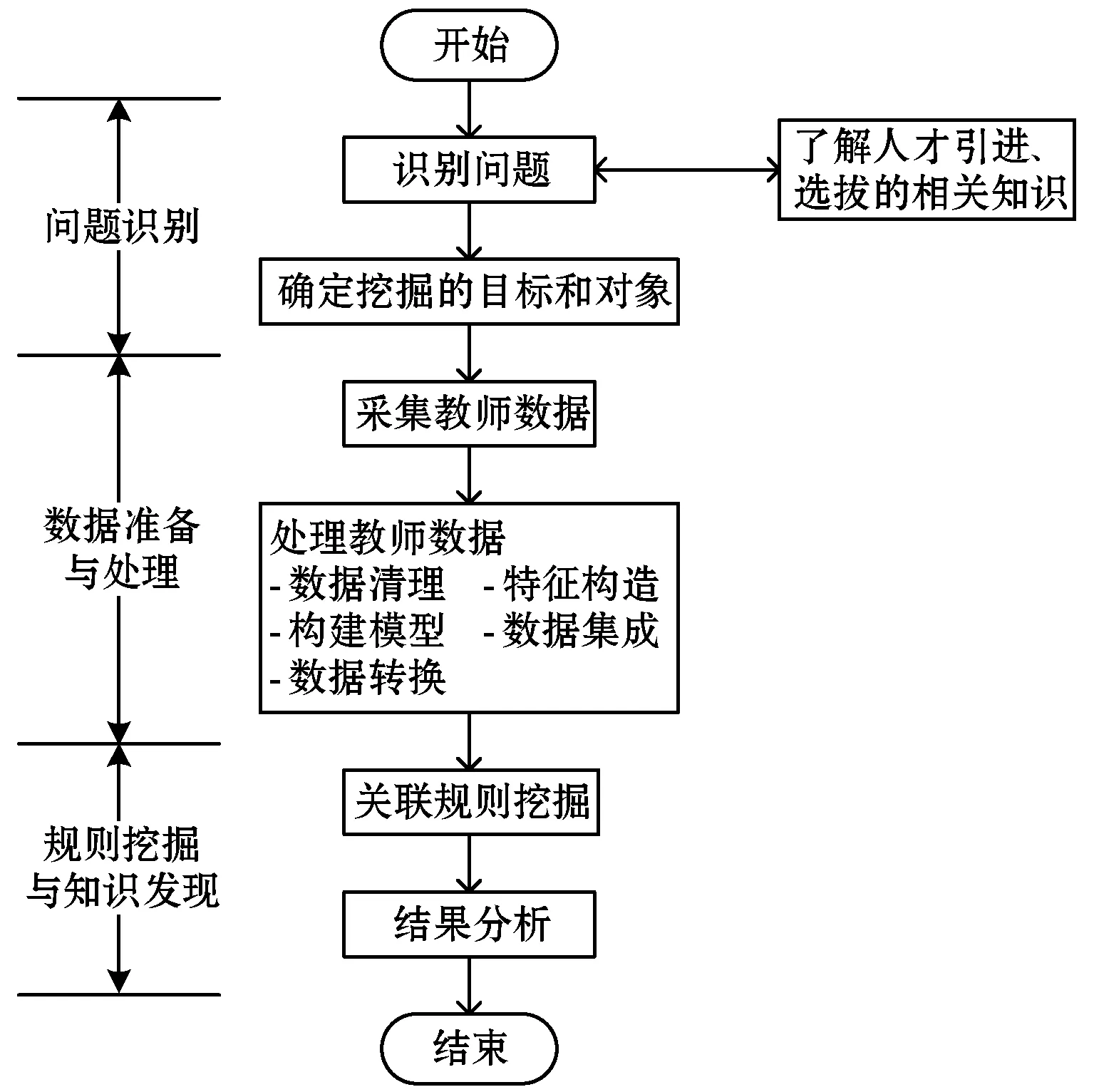
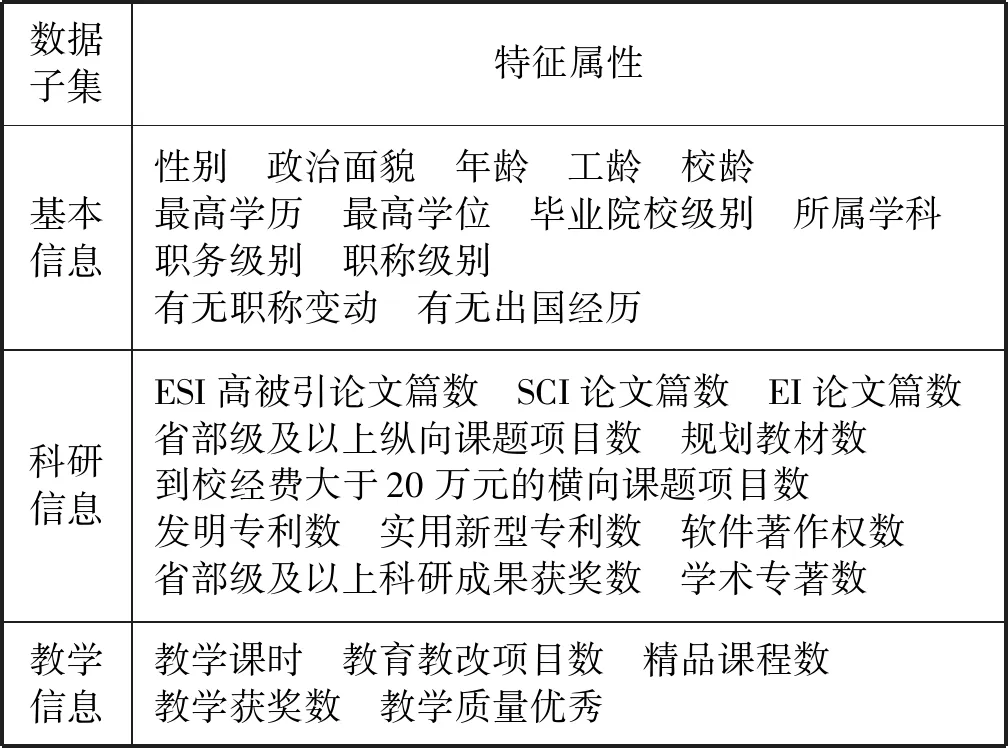
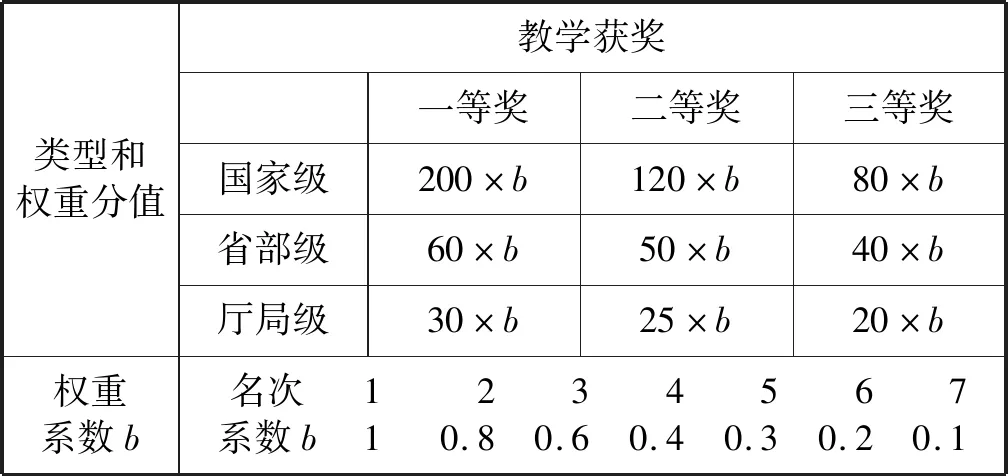
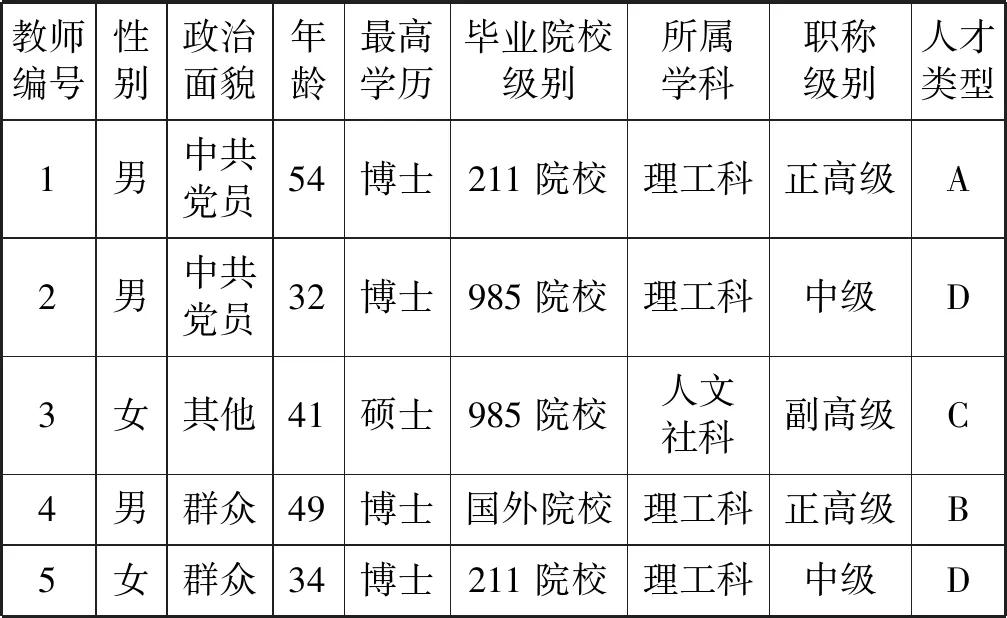
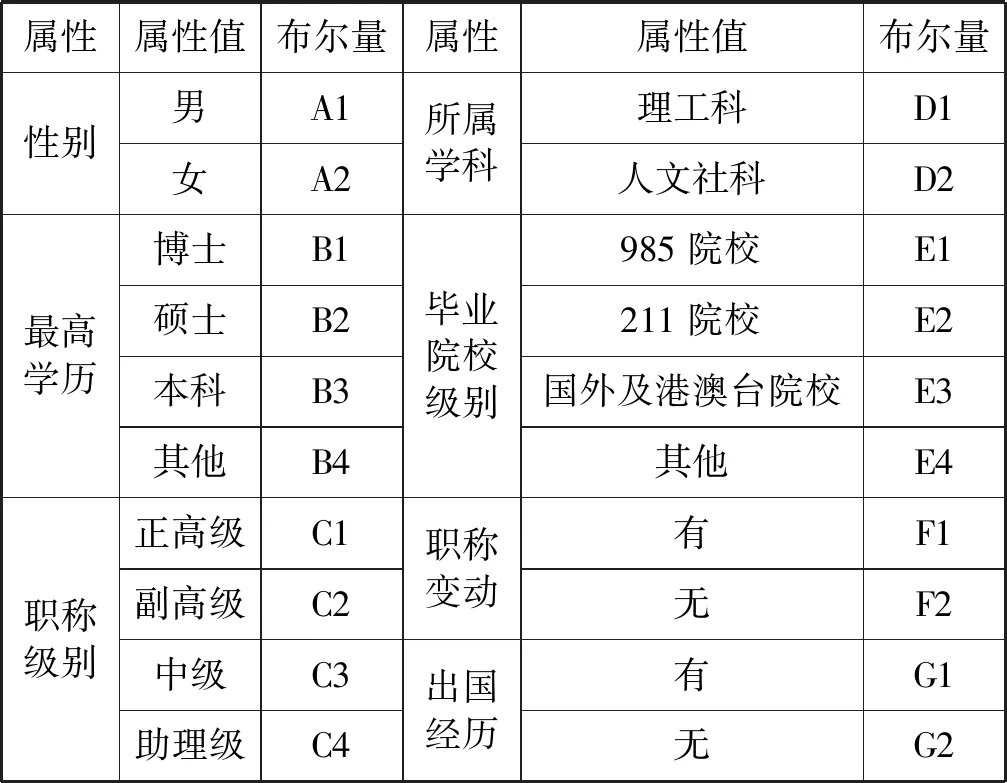
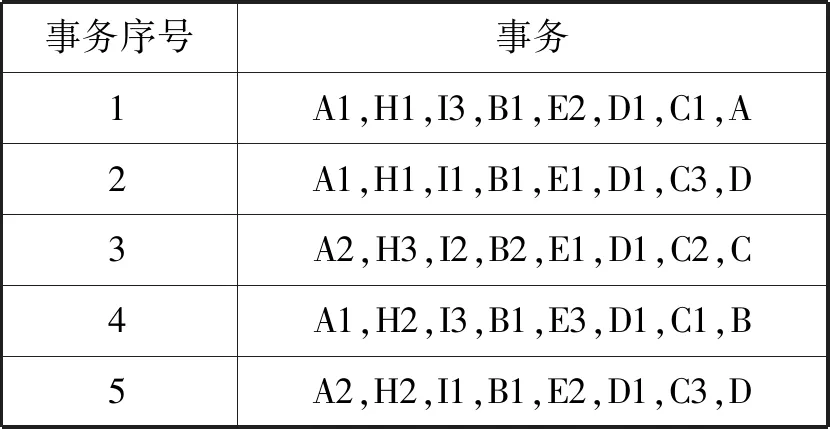
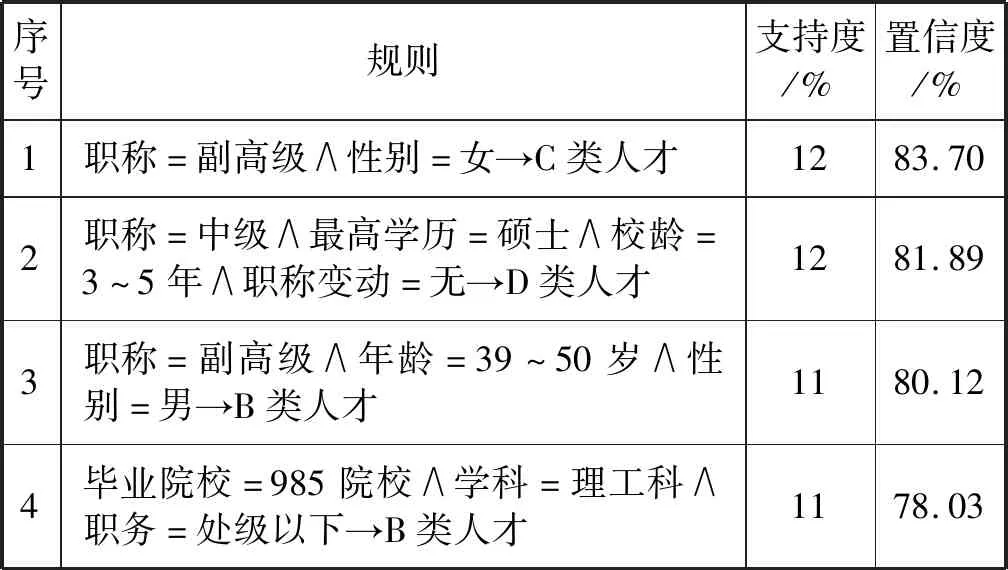
(3) 若C1 根据性质5连接两个频繁(k-1)-项集I1和I2的PF-List,得到频繁k-项集的过程,如算法2所示。 算法2连接频繁(k-1)-项集的PF-List 输入: PFL(I1),PFL(I2),最小支持度minSup 输出: 频繁k-项集Fk,PFL(Fk) 1:Fk←∅,PFL(Fk)←∅; 2: 初始化i=0,j=0,C1=0,C2=0; 4: for each PFL(I1)中的节点Nxdo 5: for each PFL(I2)中的节点Nydo 6: ifNx与Ny不存在祖先-后代关系then 7:C1=C1-Nx.count; 8:C2=C2-Ny.count; 9: ifC1 10: return null; 11: else 12:Fk=I1∪I2; 13: PFL(Fk)←{ 14: end if 15: end for 17: returnFk, PFL(Fk); 性质6父子等价剪枝策略[12]。给定项集F和项i,且i∉F。如果F的支持度等于F∪{i}的支持度,即support(F)=support(F∪{i})。则对于任意项集L,若L∩F=∅且i∉L,则L∪F的支持度等于L∪F∪{i}的支持度,即support(L∪F)=support(L∪F∪{i})。 证明:设I1=L∪F,I2=L∪F∪{i},一个包含I1但不包含I2的事务T,由于i∈I2但i∉I1,因此i∉T。由于support(F)=support(F∪{i}),说明如果事务包含F的话,则肯定包含{i}。由于事务T包含I1且I1=L∪F,说明事务T包含F,则事务T包含{i},即i∈T,与上面矛盾。因此如果事务T包含I1的话则必包含I2,则support(L∪F)=support(L∪F∪{i})。证毕。 例如,项集{bk}的PFL({bk})={<(1,7):2>},项集{bk}和项集{dk}连接得到的项集{bdk}的PFL({bdk})={<(1,7):2>},项集{bk}的支持度计数等于项集{bdk}的支持度计数,即support({bk})=support({bdk})。那么模式搜索树中,代表项集{bdk}节点的所有子节点项集的支持度都可以根据性质6得到,无需再遍历树。因此,剪掉模式搜索树中以{bdk}为根节点的子树。 PFLFIM算法主要包括四个步骤:(1) 扫描事务数据库DB,得到频繁1-项集F1,构建PFC-tree。(2) 遍历PFC-tree,得到频繁1-项集F1对应的PF-List。(3) 连接两个频繁1-项集的PF-list,得到频繁2-项集,并使用包含索引策略节省连接时间。(4) 使用模式搜索树代表搜索空间来挖掘频繁k-项集,并使用提前停止交集和父子等价策略对模式搜索树进行剪枝操作。结合前面提到的算法1和算法2,PFLFIM算法如算法3所示。 算法3PFLFIM算法 输入: 事务数据库DB,最小支持度minSup 输出: 频繁项集F 1:F←∅; 2: 扫描数据库DB,得到频繁1-项集F1,F=F∪F1; 3: PFC-tree=BuildingPFC_Tree(DB,minSup); 4: 遍历PFC-tree,得到F1的PF-List和包含索引subsume; 5: for eachF1中的项集{i} do 6: ifsubsume({i})≠∅ then 7: for eachsubsume({i})中的子集{j} do 8:F2={i}∪{j}, F2.count={i}.count, F=F∪F2; 9: end for 10: else for eachF1中其他项集{j} do 11:F2=Intersection(PFL({i}), PFL({j}),minSup), F=F∪F2; 12: end for 13: end if 14: end for 15: for eachF2中的项集{ixiy}(ix≤Liy) do 16: Cad_items←{i|i∈F1且ix≤Li}; 17: for each Cad_items中的项ido 18:P1={ixiy},P2=P1[0]∪{i}; 19: PFL(P)=Intersection(PFL(P1), PFL(P2),minSup); 20:F=F∪P; 21: end for 22: returnF; 通过比较PFLFIM算法与FIN算法和negFIN算法在挖掘频繁项集时使用的时间和占用的内存,验证PFLFIM算法的性能。为了保证实验结果的公平有效,在同一台机器上运行三种算法并比较结果,从而避免其他客观因素带来的性能差异。实验在一台内存为8 GB,CPU为Intel(R) Core(TM) i5-2430M @ 2.40 GHz,操作系统为Windows 10专业版的PC上进行,所有算法均用Java语言编写。 由于不同算法在不同特征的数据集上的表现差异较大,分别选择稠密数据集Pumsb和稀疏数据集Retail来完成实验,这两个数据集是从频繁模式挖掘测评比赛官方网站上下载的真实数据集。其中:Pumsb数据集记录的是人口普查数据,含有大量的项目和事务,整体规模较大,即使在较高的最小支持度下也包含大量的频繁项集;Retail数据集来源于比利时某零售店的销售数据,是具有代表性的、十分稀疏的数据集,常用于频繁项集挖掘的研究。两个数据集的基本情况如表4所示。 表4 数据集及特征 在相同的数据集下,将PFLFIM算法的挖掘结果与FIN算法和negFIN算法的挖掘结果进行比较,发现当最小支持度相同时,3种算法挖掘出的频繁项集的内容和数量一致,说明使用PFLFIM算法挖掘频繁项集是正确的。在Pumsb数据集下,三种算法挖掘出的频繁项集的数量如表5所示。 表5 Pumsb数据集下频繁项集数量 图6展示了三种算法在Pumsb数据集上的运行情况,其中图6(a)和图6(b)分别是三种算法在运行时间和最大内存占用上的对比。从图6(a)中可以看出,在不同的最小支持度下,PFLFIM算法的运行速度是最快的。在最小支持度较大时,三种算法的运行时间相差不大,但是随着最小支持度的减小,三种算法运行时间的差距被不断拉大,当最小支持度小于55%时,可以观察到PFLFIM算法在运行时间上的优势。从图6(b)可以看出,随着最小支持度的减少,三种算法的内存消耗均逐渐增大,但是PFLFIM算法的内存消耗始终小于其他两种算法。 (a) 运行时间 (b) 最大内存占用图6 三种算法在Pumsb数据集上的运行情况 图7展示了三种算法在Retail数据集上的运行情况。图7(a)是三种算法在运行时间上的对比,从图中可以看出三种算法在Retail数据集上的运行比较稳定,随着最小支持度的减小,运行时间变化不大,但是PFLFIM算法始终比其他两种算法的运行时间少。图7(b)是三种算法在最大内存占用上的对比,从中可以看出随着最小支持度的变化,三种算法的内存消耗变化不明显。这是因为Retail数据集十分稀疏,挖掘过程中占用的内存本就不多,但还是可以看出,PFLFIM算法在内存消耗上略优于其他两种算法。 (a) 运行时间 (b) 最大内存占用图7 三种算法在Retail数据集上的运行情况 由上面两组实验可以发现,PFLFIM算法在运行时间和内存占用方面都优于FIN算法和negFIN算法。相比于FIN算法,PFLFIM算法通过比较两个节点的PF-List就可以判断二者之间的祖先-后代关系,节省了多次遍历树查找祖先节点的时间。相比于negFIN算法,PFLFIM算法的节点信息所占的空间少,而且连接过程简单。PFLFIM算法还使用了包含索引、提前停止交集和父子等价的优化策略,避免产生大量冗余的PF-List,减少了内存占用,加快了挖掘频繁项集的速度。此外,Pumsb数据集是稠密的,Retail数据集是稀疏的,通过理论分析和实验结果表明,PFLFIM算法适用于在稠密数据库中挖掘频繁项集,同样也适用于稀疏数据库。 将PFLFIM算法应用于某高校人力资源管理系统中,对该系统中专任教师的基本信息、科研信息和教学信息进行规则挖掘,从中提取隐含的、有用的信息,寻找影响人才发展的因素,为高校管理者在人才引进和选拔中提供决策支持,总体挖掘流程如图8所示。本文使用的人力资源数据取自国内一所双一流重点建设高校,包含了2 554名专任教师的基本信息、科研信息和教学信息,数据中隐去了工号、姓名、身份证号等个人隐私信息。 图8 关联规则挖掘流程 应用本文算法解决问题的主要目标是寻找影响人才发展的因素,所以需要整理高校教师的基本信息、科研信息和教学信息,建立人才分类模型,选取与高校人才发展可能相关的特征。数据处理主要包括数据清理、特征构造、人才模型构建、数据集成和数据变换五个步骤。 (1) 数据清理。由于原始数据多存在不完整性和不一致性,需要清洗掉不完整的数据,并纠正数据中的不一致性。比如,删除刚入校不久信息不完善的教师。清理后共有1 622条教师数据。 (2) 特征构造。基本信息、科研信息和教学信息中有许多特征是与挖掘任务无关的,如民族、项目经费、授课班级等。为了去掉多余的特征,需要进行特征构造。根据高校的实际情况,同时结合专家意见,构造的各数据子集的特征属性如表6所示。 表6 特征属性 (3) 人才模型构建。设科研信息的第i个特征属性为Si,对应的权重分值为wi,教学信息的第j个特征属性为Ej,对应的权重分值为vj,通过分析客户细分模型和现有的人才模型构建方法[13],得到人才类型H的计算式表示为: (5) 续表7 (4) 数据集成。将教师基本信息和人才类型利用教师编号匹配并连接在一起,形成完整的数据集,组成高校人才信息表,其中部分数据如表8所示。 表8 高校人才信息表 (5) 数据转换。数据转换是将数据变换为适合挖掘的形式。首先需要对数值型属性进行离散化处理,例如采用深度等分划法,将年龄划分为若干个区间;对类别型属性进行变量值归约,例如将所属学科归约为“理工科和人文社科”两类。关联规则挖掘中各属性值均为布尔类型,因此需要将各个属性值转化为布尔量,部分属性的转化如表9所示。 表9 属性转化表 利用属性转化表将原始数据库转换成布尔型的事务数据库,如表10所示。 表10 事务数据库 使用上文处理后的数据进行实验,将PFLFIM算法与FIN算法和negFIN算法进行比较,发现当最小支持度相同时,挖掘出的频繁项集的内容和数量相同。三种算法在不同最小支持度下挖掘频繁项集的运行时间如图9所示。可以看出,随着支持度的变化,PFLFIM算法的运行时间始终较其他两种算法少,说明PFLFIM算法适用于该数据集,且挖掘速度较快。 图9 三种算法在高校人才数据集上的运行时间 应用PFLFIM算法对转换后的高校人才信息进行关联规则挖掘,找出支持度不小于最小支持度且置信度不小于最小置信度的强关联规则。设最小支持度为10%,最小置信度为70%,去掉结果中互相包含且无意义的规则,只保留与挖掘目标相符合的、置信度较高的且对决策有参考价值的规则,最后得到的结果如表11所示。 表11 关联规则挖掘结果 续表11 分析表11中的规则可以得到下述信息: (1) 高学历高职称且在校期间有过职称变动的教师,多为教学科研型人才。在人才引进时,多注意引进高学历高职称的人才,一方面能够在一定程度上优化人才队伍,另一方面能够有效地带动高校发展。 (2) 有重点高校学习经历的理工科教师,更容易向科研型人才发展。在引进科研岗位的人才时,应优先考虑毕业于名校的博士研究生,这样不但可以在一定程度上改善高校教师的学历结构,还能促进高校科研水平的提升。 (3) 男性教师偏向于向科研型人才发展,女性教师偏向于向教学型人才发展,说明高校教师在发展上存在一定的性别差异。因此在人才引进时,应充分考虑人才的性别差异,为其制定合适的发展道路。 (4) 校龄小于5年、学历一般且无职称变动的教师,教学和科研能力不太突出,这与他们来校不久有很大关系。但是这类人员大多有较大的发展潜力,高校管理者应多关注这类教师的工作,制定适合他们的培养机制,帮助他们迅速成长起来。在人才引进时也应多关注这类有潜力的人员,为高校的发展注入新鲜力量。 通过分析以上信息发现,挖掘得出的规则与现实情况基本符合,一些没有预料的结果也客观反映了实际情况。通过分析挖掘出来的规则,发现了影响人才发展的因素,为高校人才引进和选拔提供了策略,也为高校管理者制定决策提供了科学依据。 本文通过对FP-growth类算法进行研究,提出了一种基于PF-List的频繁项集挖掘算法(PFLFIM)。该算法主要有以下优势:(1) 使用PF-List表示项集,通过简单比较两个项集的PF-List就可以直接连接得到频繁项集,降低了算法的时间复杂度。(2) 使用包含索引、提前停止交集和父子等价策略对搜索空间进行优化,减少了内存占用。将PFLFIM算法与FIN算法和negFIN算法结合实验进行比较,结果表明PFLFIM算法在挖掘时间和内存占用上均有较高的效率。将该算法应用于对某高校专任教师的基本信息和人才类型进行关联规则挖掘上,从中提取潜在的有价值的信息,发现影响人才发展的因素,并且为高校人才引进和选拔提供科学依据,从而促进高校的全面发展,提高高校的竞争力。
2.2 PFLFIM算法描述
3 实验结果与分析

4 PFLFIM算法在高校人才引进中应用
4.1 数据处理
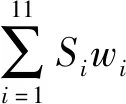
4.2 关联规则挖掘


4.3 规则分析
5 结 语
