数理统计在生产质量中的应用

戴璠

【摘 要】 数理统计是一门以概率论为基础的学科。由于随机现象无处不在，使得数理统计的原理和方法在生产中得到了广泛的应用，在国民经济和科技领域中的地位越來越重要。随着数理统计的发展，让人们对实际问题作出了更加准确的决策。本文主要围绕着数理统计中的参数估计、假设检验、方差分析等知识来探讨数理统计在生产质量管理中的应用。

【关键词】 数理统计 参数估计 回归分析

1.引 言

在工业品质管理中尤其重要的就是产品寿命的问题。寿命试验是一种破坏性试验，可以运用参数估计来估计产品的均值，再用假设检验来检验这批产品是否合格，这样可以抽取少量产品来试验减少了一定的损失;在使用新的生产工艺时，要检验两种不同的生产方法生产同类产品的优良率是否有显著差异以及在生产过程中因原材料、设备调整以及工艺参数等条件的变化而造成生产废品的出现是哪些因素造成的，这就可以运用方差分析的方法来判断。数理统计中置信区间还可以运用到风险价值中，是一种企业进行风险管理和运用收益风险比率进行决策的工具和方法。

2.数理统计在生产质量管理中的应用

在实际生产问题中，持续增加某种因素会不会使生产的产品质量有所上升还是下降，它们之间是否存在线性关系，这是一个需要研究的问题。为此可以通过数理统计中的回归分析来分析它们是否具有线性关系从而帮助我们从一个因素添加值去估计最终产品所获得的质量高低。

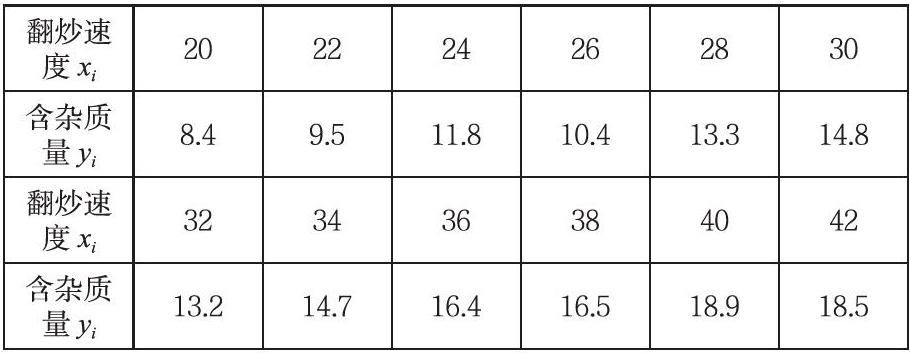
实例：以下是某茶厂的生产记录，其中xi为翻炒速度，yi为x=xi时所生产茶叶的含杂质量（单位：%），判断翻炒速度xi与含杂质量yi是否具有线性关系。

翻炒速度xi 20 22 24 26 28 30

含杂质量yi 8.4 9.5 11.8 10.4 13.3 14.8

翻炒速度xi 32 34 36 38 40 42

含杂质量yi 13.2 14.7 16.4 16.5 18.9 18.5

解：

（1）判断是否呈线性关系

首先将点以散点图的形式画在直角坐标系中。散点图大致呈现直线状，假设有线性关系，模型为：

经计算可得

以及

因此，即可建立以下的经验回归方程：

（2）对上述线性回归的在显著水平为下进行显著性检验：

构造t统计量：

故拒绝原假设，认为回归效果显著，即之间存在线性关系。

（3）回归系数b的置信区间

当回归效果显著时，对系数b进行区间估计，由于可得在置信度为1-0.05下，b 的置信区间为：

即为.

3.结束语

数理统计知识在现在的生产，生活中不仅仅可以运用到本文所提出的两个典型事例，它在生产质量管理中的应用是随处可见的。本文论述的目的在于明确数理统计知识在现今生产质量管理中的重要地位，引起人们关注生活，关注数理统计的知识。学好数理统计知识并且能够在生活中得到实际的应用，会让我们更深入地了解问题的本质.

【参考文献】

[1] 何迎辉，闵华玲.数理统计[M].北京：高等教育出版社，1989.

[2] 潘承毅，何迎辉.数理统计的原理与方法[M].上海：同济大学出版社，1993.

[3] 李维娜，李  敏.假设检验在卷烟质量分析中的应用[J].中国质量，2005，18（2）：75-76

[4] 张必真，章渭基.数理统计在质量管理中的应用[J].数理统计与管理，1994，04.008

[5] 金  苗，王尔贤.数理统计杂电池生产中的应用[J].电源技术，2006，03.20

[6] 于潇宇，焦永泉，付凤荣.数理统计在选煤质量管理中的应用[J].选煤技术，20006，03.30