突出数学思想方法教学，注重解题思想能力的培养

隋秀霞

摘 要：初中数学教学与学习必须借助思想方法的教学才能有重大突破。数学思想方法要很好地渗透到初中数学教学中，在教学过程中要重视思想方法的训练，注意教学思想方法的归纳，把握数学思想方法教学要求的层次，把数学思想方法的教学渗透贯穿于整个教学过程，逐步积累，让学生对数学思想方法的认识由浅入深、由表及里，逐渐达到一定的认知高度，从而自觉地运用。

关键词：数学思想方法;必要性;途径

一、突出数学思想方法教学的必要性

1.教育目的的需要。数学家波利亚曾统计学生毕业后，研究数学和从事数学教育的人占1%，使用数学的人占27%，基本不用或很少用数学的人占70%，对于大多数学生来说，数学思想方法比形式化的数学知识更加重要，因为前者更具有普遍性。

2.掌握数学学科基本结构的需要。众所周知，初中数学学科体系存在两条主线，一条明线是数学知识体系，反映知识间纵向联系;另一条是数学方法系统，反映知识的横向联系，例如数学建模思想更加突出其重要性。

3.有利于创造能力的培养。创造能力是数学素质的一个重要层面，现代教学论认为，数学思想方法的教学是把传统的知识型的教学转化为能力型教学的关键，是培养有创造型人才的良好手段和渠道。掌握数学思想方法是学生形成能力的必要条件，对于提高学生的数学思维有着至关重要的作用，淡化数学思想方法教学必将阻碍学生能力的发展和数学素质的提高。

二、在教学中突出思想方法教学的途径

1.挖掘提炼数学思想方法，实现知识掌握由难到易。由于学科教材的编排必须考虑到学科内容的内在联系及逻辑系统，因此，数学思想方法只能从相关内容中去体现，具有潜形态。教师应当将这些思想由潜形态转变为现形态，使学生由对方法的朦胧感受、死记硬背转化为明细的理解，掌握和灵活运用，最终完成对数学知识、数学方法的本质认识。例如：在教授“一元一次不等式组的解集”第一课时中，例题呈现了解的四种情况：同大取大，同小取小，大小小大取中间，有的教师不注重数形结合，而是急于让学生背顺口溜，讲了一节课学生还有的是不知怎么找公共解。其实，无论哪种情况，在同一数轴上表示两个不等式的解集“双线部分即为公共部分，即为不等式组的解集”。这里的双线部分就是关键点，它涵盖了四种解集情况的共同点。简单易行，易于掌握。为什么非要让学生背呢？数形结合思想，分类讨论思想，转化思想，建模思想，类比思想，函数思想等都是初中学习的重要思想，我们应有系统地培养学生的这些数学思想，不仅有利于培养学生的数学素养，而且为后续发展提供动力。

2.抓住知识的发生过程，强化数学思想数学知识的发现过程，实际上也是数学思想方法的发生过程，但对于学生来说，这种发现或发生過程往往被教材浓缩甚至隐去。例如在对定理公式的认识推导过程中如何让学生亲历探索过程，体会发现知识的过程，汲取更多的思维营养，促进学生思维能力的形成和发展，是教学中必须考虑的又一方面。数学知识的发现过程，实际上也是数学思想方法的发生过程，但对于学生来说，这种发现或发生过程往往被教材浓缩甚至隐去。例如在对定理公式的认识推导过程中如何让学生亲历探索过程，体会发现知识的过程，汲取更多的思维营养，促进学生思维能力的形成和发展，是教学中必须考虑的又一方面。

3.加强过程教学，提高学生参与有效的数学学习，教师应引导学生从事观察、实验、猜想、验证、推理与交流等数学活动，让学生经历知识的形成与应用的过程，更好地理解数学知识，掌握必要的基础与基本技能，发展应用数学知识的意识与能力。在学生的学习过程中，“经历了过程”往往比“直接得知结果”印象更深刻，而这种经历任何讲解代替不了。例如，在教学“鸡兔同笼”一节时，题例：“今有鸡兔同笼，上有头三五，下有九十四足，问鸡兔各几何？”我设计这样的一个情境，假如我拿两颗大白菜放笼子上面，你猜会怎样？学生答：鸡伸出头来啄食，兔子两只前脚趴在笼子上面啃菜叶。师问：那么此时笼子底下站了几条腿？

学生沉思：30秒钟幡然醒悟，70条腿，多余的兔腿在笼顶，于是很快列出方程。此题给学生建立模型：求两个未知量，设两个未知数，找准两个等量关系，列出两个方程，这样对今后比较复杂的题目学生也肯定是轻车熟路了。

4.化隐为显，打通思维屏障，使知识结构系统化，教材中的许多知识，从思维方法角度去分析，更容易把握其本质联系，使原来看似孤立和静止的知识点成为有机联系的动态的知识发展过程。因此，在教学中突出数学思想，把对方法的认识提升到数学思想运用的高度，有利于减轻学生记议负担，沟通知识联系，把握方法本质，使学生逐步掌握系统、完整的知识结构，例如，在研究二次函数的应用问题，教师应该教会学生把生活问题数学化，加强函数模型与生活实际的联系，应该从思想方面指导学生明白，无论是路桥问题、利润问题，还是其他各种二次函数问题，无非就是关系式，图像，定点最值，条件最值，已知函数值求解二次方程等问题。而不应该一题一模样的单列去讲，表面看来分专题，实际上把只是一个数学问题弄得支离破碎，没有抓住问题的核心思想。在这种综合应用多种数学思想方法解决问题的过程中，学生能进一步加深对数学思想方法的理解。

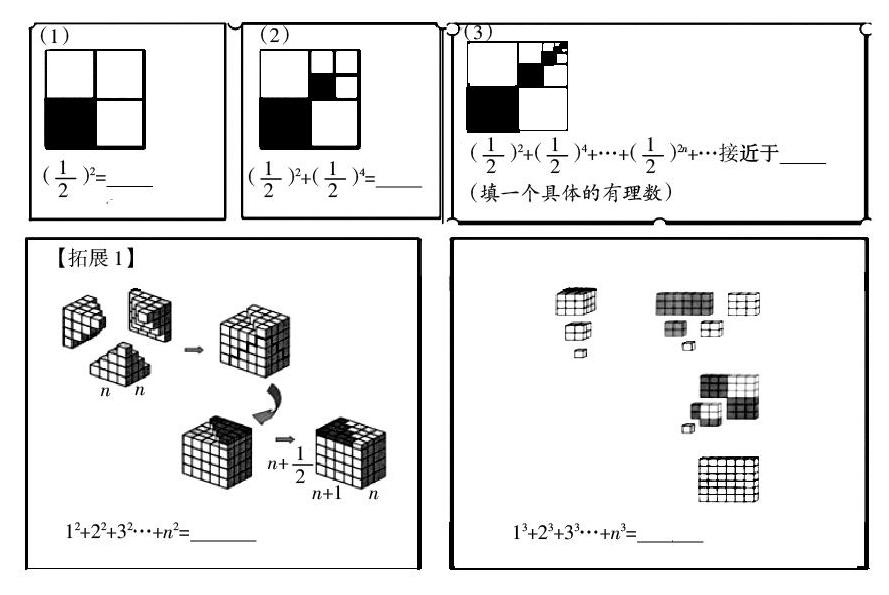
5.巧用无字的证明，加强数形结合思想方法的教学。无字的证明是指仅用图像而无需文字解释就能不证自明的数学命题。数学证明中包含的美丽与精巧实在是一道亮丽的风景，而这种亮丽甚至不需要用语言来描述，这种证明方式被认为数学证明中更为优雅与条理。借助图形来表示数量或数量关系，或借助数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合，也是一种无字的证明。我们善于搜集这样的题目，有利于开阔学生的数学思维，加强数学魅力与兴趣教学，例如下题及其拓展就很好地体现数形结合思想。

6.综合应用，深化理解数学思想方法，在解决某一数学问题时，往往需要综合使用多种思考方法。这就决定了数学思想方法教学不是单一的、孤立的，而应让学生能综合应用多种数学思想方法解决问题。例如这是生活中一个有趣的数学题：（1）汽水1元1瓶，2个空瓶换一瓶，20元最多可以喝多少瓶？生1答：20+10+5+2+1+1+1=40瓶;（2）汽水1元1瓶，5个空瓶换一瓶，20元最多可以喝多少瓶？2000元最多可以喝多少瓶？生2答：20+4+1=25瓶;第3个问题换成2000元怎么算呢？还按照前面的做法行吗？显然计算很慢。生4答：2000÷0.8=2500瓶，同样一个题目的变式训练，为什么有的人很快计算出来了呢？数学考查的核心能力是解题方法和解题思想，而这个问题的本质是每瓶汽水最终多少钱？也即优惠完了之后的价格是多少？变得是数量，不变的是思想，他们是千变万化的不变，他们是应变能力的源泉，他们是区分能力的关键，掌握解题方法，领悟解题思想是学好数学的关键之处。

总之，作为初中数学工作者，做好数学思想方法教学，培养学生解题能力是时代赋予我们的使命，也是我们教学中应该积极探讨的问题，中学数学的教学与学习必须借助思想方法教学才能有重大的突破。

编辑 温雪莲