基于SVM-Markov模型的短期风速组合预测

鲍庭瑞

(安徽工业职业技术学院 ，安徽 铜陵 244000)

风速预测方法有数值天气预报预测和统计预测2大类,前者依靠气象部门提供气象数据,通过复杂的数学模型对风速进行预测,精确度高,但气象预报数据更新频率低,不适用于短期和超短期风速预测[1]。统计预测方法依靠历史风速数据,建立具有泛化性能的预测模型,由于其预测算法可以依据历史数据的更新及时调整,适合于超短期预测。常用的统计预测方法有混沌预测法[2],神经网络法[3],支持向量机等[4]。单一的预测模型得到的预测精度有限,组合模型将多种具有不同特点的预测模型的到的的预测结果按照一定的权重进行组合,可以提高预测精度。本文提出一种基于支持向量机(SVM)与马尔可夫链(Markov)的组合预测方法,通过自适应调整组合权值,提高了预测精度。

1 回归支持向量机预测

支持向量机分为线性可分、非线性可分和核函数映射3种情况。回归支持向量机(support vector regression,SVR)主要有Vapnik提出的ε-SVR,ε为不敏感函数。ε-SVR利用非线性映射将样本数据映射到一个高维特征空间, 然后在此高维特征空间上进行线性回归分析。支持向量机基本原理在文献[4]中给出了详细表述。

基于SVR的风速预测具体步骤如下:①样本数据提取。将历史风速样本分为训练集和测试集。风速时间序列记为{xt,t=1,2,…,n},将原数据序列进行相空间重构,构造样本对(Xt,Yt),其中Xt={xt-m,xt-m+1,…,xt-1}，Yt=xt,m为输入向量的维数,通过仿真实验确定维数m为4。用训练集样本训练SVR回归预测模型。②采用二次网格搜索法确定ε、C和σ最优选取,可以有效地避免过拟合现象。③利用训练好的回归模型预测测试集风速样本。④将风速预测值与风速实际值进行比较, 计算误差,评价模型性能。

2 马尔科夫区间预测

马尔科夫区间预测是根据系统状态转移概率预测未来风速的概率密度及概率分布,该预测方法反映了随机风速时间上相依性[5]。将历史风速划分为m个状态,每个状态对应于等间隔划分的风速区间。初始分布pn表示n时刻风速在各状态的分布概率的列向量,定义为:

(1)

(1)计算转移频数矩阵。设pij为风速从状态vi转移到状态vj的概率,在所有历史风速样本中判断相邻时刻2个风速所属的区间,设分别为Di和Dj。统计风速从区间Di向区间Di演变的次数Nij,得到转移频数矩阵:

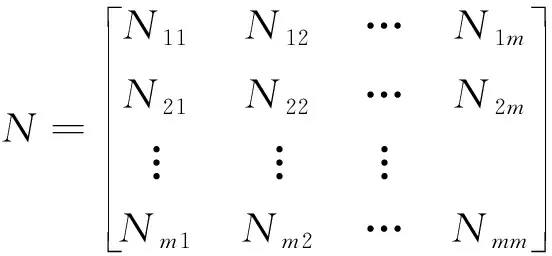
(2)

(2)计算转移概率矩阵。根据转移频数矩阵按式(3)计算所有状态间的转移概率。

(3)

所有pij构成转移概率矩阵:

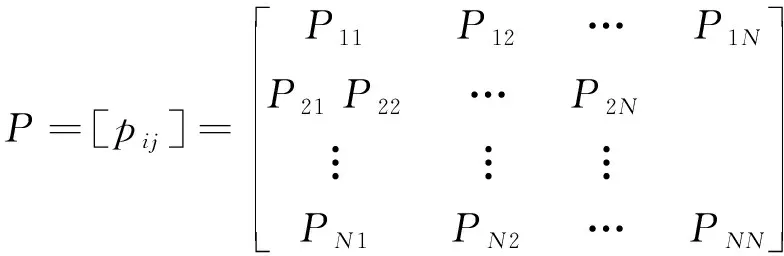
(4)

(3)计算转移概率密度。利用转移概率矩阵和零时刻的初始分布可以通过式(5)计算所有时刻所有状态的概率密度函数:

Pn+1=P·Pn

(5)

(4)计算置信区间及预测值。对于风速v,根据转移概率密度计算其置信度为1-α的置信区间[vminvmax],该区间以1-α的概率包含实际值。这样的区间并不唯一,在所有符合条件的区间中选择区间宽度最小的区间,因为区间宽度越大,符合条件的样本越多,参考价值越小。将置信区间的中值作为Markov预测值。

3 自适应权值组合预测

将SVM风速预测值与Markov风速预测值按照一定权值进行组合得到组合预测值。权值根据误差情况自适应调整。设风速的SVM预测值为vSVM,Markov预测值为vMarkov,风速实际值为vreal,则有:

组合预测值为:

vZH=k1·vSVM+k2·vMarkov

(6)

SVM预测误差为:

r1=vSVM-vreal

(7)

Markov预测误差为:

r2=vMarkov-vreal

(8)

组合预测误差为:

r3=vZH-vreal

(9)

其中,k1、k2为权值。权值按照前一时刻预测误差进行修正,随着数据的更新而不断调整。权值调整流程图如图1所示。

图1 权重调整流程图

设初始时刻t的权值为k1=k2=0.5,在预测t+1时刻风速时,由于t时刻的实际值已知,这样可以得出按初始权值组合的预测误差,若误差在可接受范围内,如|r3|0,说明预测值大于实际值,则需要减小预测值,这时需要比较vSVM与vMarkov的大小,将其中的较小值对应的权值增大,将较大值对应的权值减小。反之,若r3<0,说明预测值小于实际值,则需要增加预测值,这时将vSVM与vMarkov中较小值对应的权重减小,将较大值对应的权重增加。更新权重后,返回到开始部分重新进行组合预测。如果经过多次更新后始终不能将误差调整到规定范围,程序将一直循环下去,这时设置循环调整次数,超过该次数则自动停止,直接输出结果,仍以初始权重进行下一步预测。通常,预测误差超过限定值的情况是客观存在的,但通过该方法,总体上必然会减小误差。

为了评价预测精确度,式(10)(12)定义了3种预测误差:平均绝对误差(EMAE)、平均绝对百分比误差(EMAPE)和均方根误差(ERMSE)。

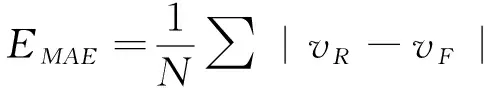
(10)

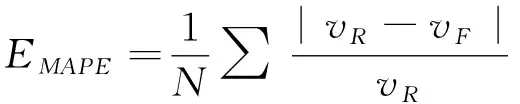
(11)

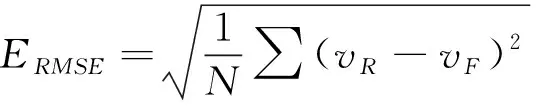
(12)

其中,N为样本个数,vR为实测值,vF为预测值。

4 算例分析

本文采用我国某风电场2012-10～12月小时风速数据对上述方法进行验证。仿真试验在MATLAB7.4下进行,仿真结果如图2、图3所示。图2给出了 Markov区间预测及其中值曲线,图3为组合预测曲线,表1为3种预测误差统计表。

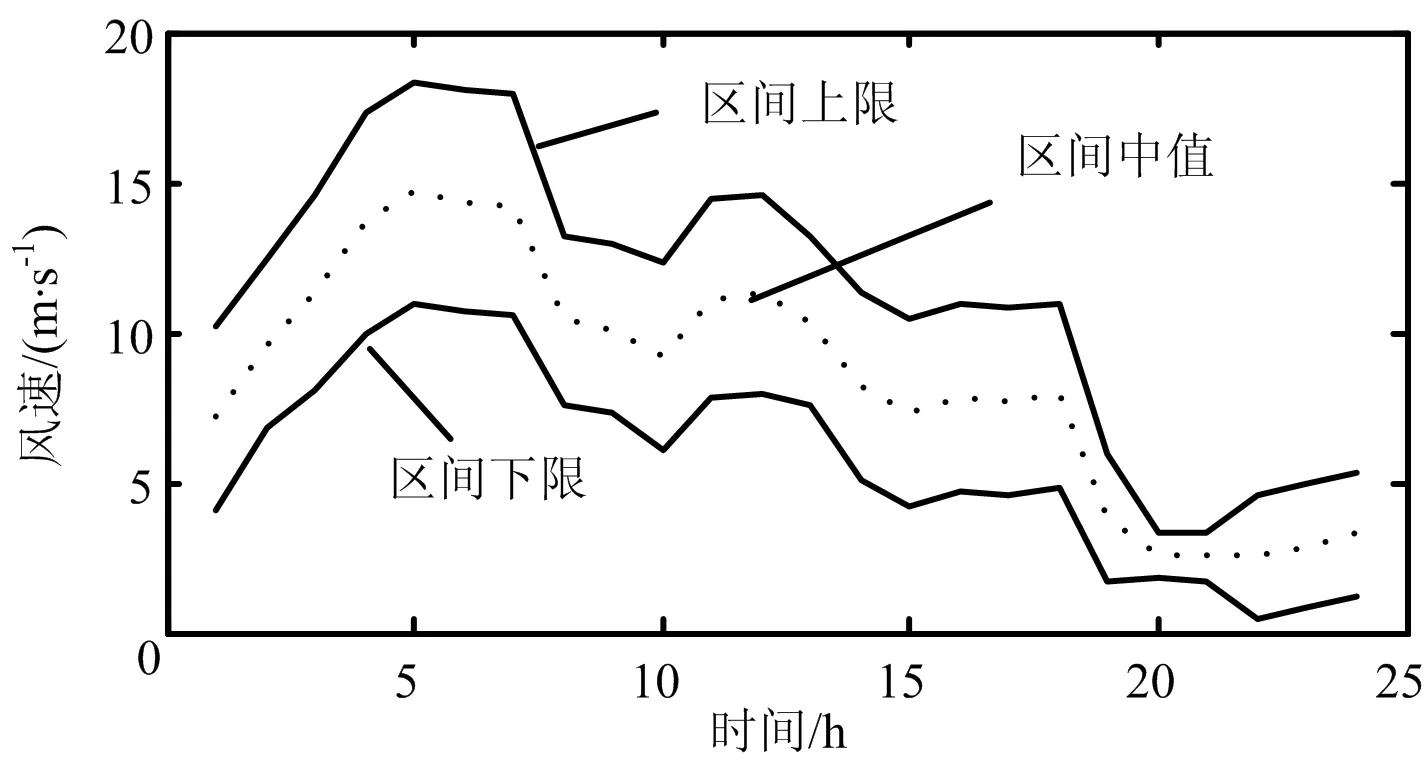
图2 Markov区间预测曲线

图3 组合预测曲线

表1 预测误差

由图2、3及表1可以看出,与实际风速相比,SVM初步预测误差及Markov区间中值预测误差都比较大,其中Markov区间中值预测误差比SVM初步预测误差大,但由于大部分预测值在实际值上下变化,经组合权重调整后的组合预测误差普遍较小。

5 结论

针对同一预测对象,不同的预测方法具有不同特点及预测误差,组合预测能够综合各种预测方法的优势得到较为精确的预测结果。但组合预测精度的提高很大程度地取决于权值的选择。本文提出的预测方法能够综合考虑已经预测出的误差情况,通过自适应调整权值,能够结合SVM初步预测及Markov区间中值预测的特点,提高预测精度。