基于Boruta-SVM的软件缺陷预测

2019-09-12金秀玲柯荣泰

山西大同大学学报(自然科学版) 2019年4期

金秀玲，柯荣泰

（闽江学院数学与数据科学学院，福建福州 350108）

随着软件生产规模和应用范围的扩大，软件缺陷是软件开发中不可避免的事情。软件缺陷会给软件开发团队带来维护的困难，给企业带来巨大损失。因此软件缺陷预测成为软件开发和软件维护中不可缺少的一部分。利用数据挖掘技术分析软件数据、预测软件缺陷是一种切实可行的解决方案，可以提高软件质量，降低测试成本。因此随着数据挖掘技术的革新，软件缺陷预测的精度将逐步提高。这不仅可以减少测试成本，还能令软件开发团队迅速找到缺陷点，从而提高工作效率。

软件组件每次执行故障的风险都是可用的，因此可以从不同的角度分析软件缺陷的故障概率。软件开发生命周期一般包括分析、设计、实现、测试和发布阶段。测试阶段应该有效地操作，以便向最终用户发布无bug 的软件。近二十年来，国内外学者对软件缺陷预测问题日益关注，各种数据挖掘技术被应用于更稳健的预测。2014年以来，软件缺陷预测问题研究中，国际上选定的缺陷预测论文概括为：基于机器学习的预测算法，处理数据，工作量预测的实证研究。研究界仍面临构建方法和许多研究机会存在一些挑战[1]。另外,随着计算机硬件的提升和深度学习技术发展，Arar 将传统人工神经网络（ANN）与新型人工蜂群（ABC）算法相结合,构建新的分类器对缺陷进行预测[2]。

在国内，随着数据挖掘技术的发展，数据挖掘技术大量用于软件缺陷的预测问题中。主要方法是使用分类器如BP神经网络、支持向量机、贝叶斯网络、LDA、随机森林等。朱永春等使用均方误差改进预测的技术对软件缺陷预测[3]。王青等人也对软件缺陷预测的起源、发展及问题做出综述[4]。王涛等构建支持向量机的软件缺陷预测模型[5]；王科欣等使用贝叶斯网络对软件缺陷预测[6]；姜慧研将蚁群优化算法与支持向量机相结合建立软件缺陷预测[7]；王铁建等基于多核字典学习对先软件缺陷进行特征选取，构建SVM 模型预测软件缺陷[8]；黄小亮等人提出了一种基于狄利克雷分布（LDA)的软件缺陷分布方法等[9]。

国内外对软件缺陷预测模型及其应用进行了大量研究，基于SVM进行软件缺陷预测分析，得到比较不错的成效。普遍存在着优化SVM模型同时，使得模型的复杂度增加，模型的参数难以确定。但在变量特征选取方面考虑甚少。特征选择有助于排除不相关特征、偏见和不必要噪音的限制来建立预测模型。因此，特征选择是模型构建的一个重要方面。传统的特征选择原理是选取最优子集，以减少特征个数，提高模型精确度，减少运行时间的目的。这样难免会造成有些与因变量相关性不够强的特征被完全忽略，造成信息丢失。软件缺陷预测的问题，是预测潜在但未暴露的缺陷，以缺陷尽早检验为原则，既可以减少修复成本，还能缩短缺陷修复时间。

Boruta特征选择方法原理是选取所有与因变量相关的特征。满足软件缺陷预测行业精益求精的要求。将Boruta 降维方法与SVM 模型结合应用在软件缺陷预测问题中。通过Boruta降维方法选取最优的软件编码度量特征，减少SVM 特征集的复杂度，同时采用交叉验证方法确定高斯径向核函数的参数，用于SVM 模型识别软件缺陷和分类的研究中。比仅使用SVM 模型预测软件缺陷的精度有显著提高。

1 相关理论

1.1 Boruta降维方法

Boruta 降维方法是一种围绕随机森林周围的包装算法,通过计算每个特征的重要性，筛选出所有与因变量具有相关性的特征集合，特征送样流程见图1。

Boruta算法运行的步骤如下：

（1）通过增加原始数据集的随机性成分，创建含有混合副本的所有特征（即阴影特征），在扩展数据集上运行随机森林分类器，采用评判特征重要性措施（平均减少精度）——即Z值，用来评估每个特征的重要性，Z值越高则意味着该特征越重要；

（2）找出阴影特征中得分最大Z值。在每次迭代中，检查一个真实特征的Z值，将特征得分高于最大阴影特征得分的真实特征标记为“重要”，将特征得分显著小于最大阴影特征得分的真实特征标记为“不重要”，并且从特征集合中删除不重要的特征；

（3）最后，重复上述步骤，直到所有特征得到确认或拒绝，或算法达到随机森林运行的一个规定的限制时，算法停止。

图1 特征选择流程图

单个特征的Z值计算公式：

一棵树中用OOB（袋外数据）样本可以得到误差e1；然后随机改变OOB中的第j列，保持其他列不变，得到误差e2；mean表示平均值；sd表示标准差。

1.2 支持向量机

SVM（support vector machine，支持向量机）是分类器算法，其核心思想是结构风险最小化原则[10]。加入该技巧，使得SVM模型能够高效地解决非线性可分情况。高斯径向核函数（RBF）保留映射到无限维空间的能力，同时能保证半正定核矩阵。径向核函数的支持向量机模型适用软件缺陷二分类问题。

软件缺陷预测是二类分类问题，对给定训练集

其中，x为样本输入变量，n为样本数量，d为样本特征维度,y为样本缺陷类别。

SVM分类决策函数：

加入核技巧解决非线性划分的问题；高斯径向核函数K：

高斯径向核函数下SVM决策变量函数变换为：

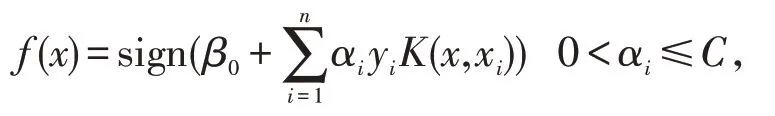
C为惩罚参数。

1.3 评价指标

评价指标用于区分预测模型的优劣，混淆矩阵是一个评价分类器性能的矩阵[11]。软件缺陷的预测是一个典型的二分类问题，根据软件缺陷预测结果可以得到一个基础的混淆矩阵,见表1。

表1 软件缺陷问题混淆矩阵

在混淆矩阵的基础上，常用的几个性能指标：

（1）准确率（Accuracy）：分类器区分正确样本的个数占所有测试样本个数的比例

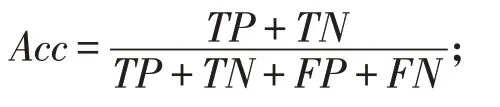
（2）精确率（Precision）：预测正确的无缺陷数据占所有预测为无缺陷类别的样本个数比例

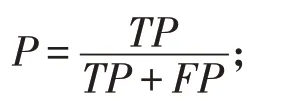
（3）召回率（recall）：衡量预测正确的无缺陷数据占无缺陷总数的比例

（4）误判率（Probability of False alarm）：衡量预测错误的有缺陷模块占总体有缺陷模块数的比例

（5）F1：常用的对精确率P和召回率R综合评价的指标

2 软件缺陷预测模型

为了提高SVM 的软件缺陷预测模型的性能，采用Boruta 算法先对数据集进行特征选择，达到降维的目的，再通过10 折交叉验证方法优化SVM 的惩罚参数C和核函数参数γ，提高SVM 的软件缺陷分类准确率，构建SVM模型。

Boruta-SVM 软件缺陷预测方法运行的步骤如下，见图2。

（1）数据准备：数据导入，对数据进行清洗，并将数据集随机分为两部分，70%的训练数据以及30%的测试数据；

（2）特征选取：利用Boruta 方法对数据进行降维，选取最优特征数据集；

（3）建立模型：利用Boruta得到的特征，适用分类器对训练数据进行训练，用10折交叉验证方法，设定径向核函数中的优化参数，得到相应的软件缺陷预测SVM模型；

（4）评价分析：利用建模的软件缺陷预测模型，对测试数据进行验证分类，将利用模型分类的结果与原结果建立混淆矩阵，分析准确率、精准率、召回率、误判率、F1值等。接着对模型性能进行对比分析。

图2 软件缺陷预测模型建立流程

3 模型验证

3.1 数据集

软件缺陷数据集为美国航天局(简称NASA)官网发布的MDP（Metric Database Program）公开数据集，是使用Java、C 以及C++语言进行开发的飞船仪表、卫星飞行控制等软件，数据库共12 个子数据集，每个数据集代表一个NASA 软件系统的代码样本，并都存在着一定的软件缺陷。实验采用数据库中的5 个子数据集，其中特征数38 个是对软件进行度量后所得度量属性个数，样本数为测试软件中的样本总数，缺陷数为含有缺陷的样本个数，缺陷率为软件的缺陷数与样本数的比值,见表2。

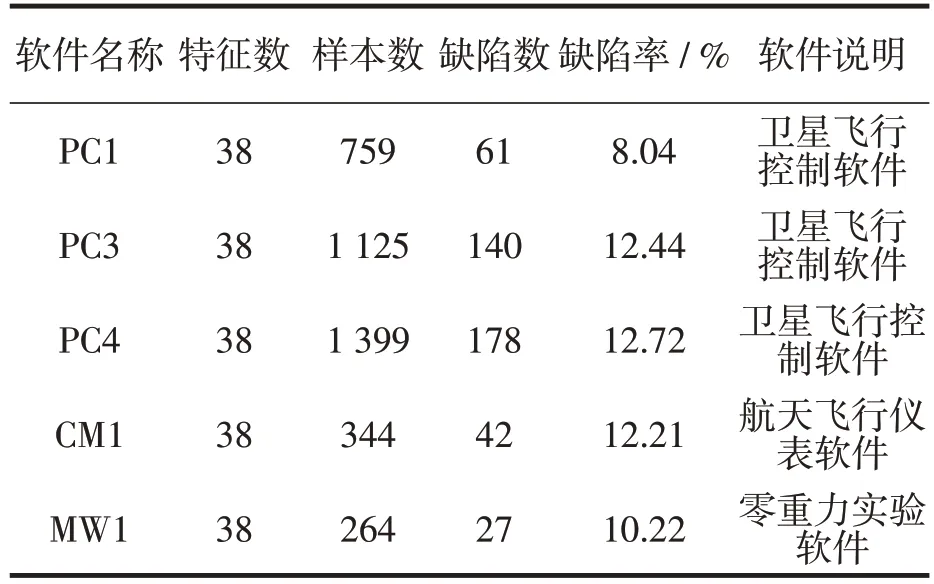
表2 NASA MDP数据子集

3.2 实验结果与分析

先对5 个数据PC1，PC3，PC4，CM1 和MW1 经过数据的清洗后，数据按照7：3 随机分成训练集和测试机。分别用于模型的构建和测试。采用Boruta算法对5个数据分别进行特征选择，维度下降到27,32,16,17和34。对于SVM模型，高斯核函数的参数C,γ参数分布设置为区间[1,100],[0.01,4]；运用10折交叉验证实验法确定构造硬度变化曲线选择最优C=4,γ=0.01，建立最终的Boruta-SVM模型。为了验证本文提出的算法是否能够获得较好的特征选择结果，利用Boruta算法对NASA MDP 数据子集进行降维，将Boruta-SVM 软件缺陷预测模型与SVM模型进行对比，对比结果如表3所示。

表3 Boruta-SVM 软件缺陷预测结果

可知，经过Boruta 方法降维后，软件缺陷预测模型的准确率与原先SVM 的，准确率都有一致提高，其中MW1 提高幅度最大为7.3%；误判率从分别下降40%，6.5%，10%，40%和50%,误判率得到一致降低，而且降幅明显；F1值也得到一致提高。结果表明Boruta—SVM 模型无论从准确率、误判率以及F1值都对分类效果提升显著。

Boruta-SVM 软件缺陷预测模型在SVM 的基础上准确率和F1值都有相应的提高，误判率也明显降低。误判率降低了，工作人员修复缺陷的速率也得到了大幅度的提高，软件出错的可能性相对之前也低了不少。因此，可以认为采用Boruta 降维方法，把特征选择结合SVM 应用于软件缺陷预测问题，Boruta-SVM 软件缺陷预测模型比原模型的分类效果更准确、更有效、且可执行性强。