基于近钻头振动数据的海底硬质地层探测方法
2019-09-12
(中国石油大学(北京) 油气资源与探测国家重点实验室,北京 102249)
海洋平台建设及自升式钻井船插桩过程中常遇到砾石层或硬夹层的卡阻,导致二次作业或造成重大工程损失。目前,通常采用地震剖面分析、海底工程取芯等方法对海底的砾石层及硬质夹层进行预警[1],成本高。已有研究利用井下低频段振动反馈钻具工作状态,高频段振动记录岩石的岩性特征的特点[2-3],开发了1种近钻头振动监测装置,该装置连接在海底勘查钻头的后部,可以利用自升式平台携带的模块钻机进行预钻探。因此,通过实时收集井下近钻头的振动数据作为砾石层及坚硬夹层的识别信号,利用时域频域图像中振动信息的关键特征确定对应的影响因素,建立海底风险地层识别分析模型和分析方法,实现对海底砾石层或硬质夹层的识别和预测。
1 近钻头振动数据采集装置
1.1 近钻头振动数据采集装置结构原理
近钻头振动采集装置见图1。

图1 近钻头振动采集与存储装置
采集装置主要采用ESM井下振动测量工具进行振动信息测量,ESM测量短节和传感器安装方式见图2。

图2 测量短节结构截面示意
系统中,坐标系原点为近钻头振动测量装置的轴心,沿钻柱轴线和径向安装3只加速度传感器,且设备上的3只加速度传感器采取两两相互垂直正交模式进行安装,可采集2个正交方向上的加速度值。
1.2 近钻头振动数据采集方案
由于不同的振动频段表征的井下振动物理意义有所不同[4-5],因此,在海底异常夹层预警方案中,首先要获取海底勘察期间的全程振动数据,获取的振动数据样本要求覆盖待测量地层的厚度。
为保证仪器可以真实地反映振动信号的波形特征。采样频率一般选取预估信号最高频率的2.5~4倍,即10~30 Hz为宜。见表1。
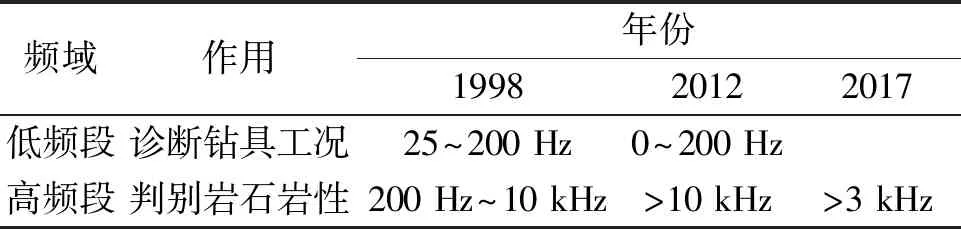
表1 振动频段划分阈值
考虑测量仪器的成本及使用效果预期,选用17 kHz的采样频率,方案见表2。

表2 采集方案
1.3 近钻头振动数据采集算法
系统的3个加速度计分别沿径向安装,输出值分别为a1、a2、a3;1个加速度计沿轴向独立安装,输出值为az;磁力计可测量角速度ω。
根据测量系统结构设计原理,采用测得物理量对钻柱不同振动特征进行表征。Xa、Ya分别为沿钻柱切向、径向的加速度测量值,Za值为轴向加速度值。根据加速度计的安装方式,3个加速度传感器测量值的表达式为
(1)
1.3.1 轴向振动
钻柱轴向振动可通过Z轴加速度计的加速度值大小及波动情况判断。Za可直接反映轴向振动加速度大小。
1.3.2 扭转振动
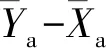
钻头-地层相互作用和摩擦力较大时产生的扭转振动,扭转振动很剧烈时,会大概率发生黏滑运动。黏滑运动是1种自激产生的剧烈扭转振动。井下发生黏滑运动时,陀螺仪所记录的实时转速会发生强烈波动。
钻柱运动特征对应的振动形式及判据见表3。

表3 主要振动特点与钻头运动特征关系
2 信号分析方法
2.1 信号处理
井下测量仪器对井下高频振动数据进行采集,井下高通滤波电路过滤反应钻具工况的频率较低的信号,保留频率更高的信号。高通滤波电路处理后的信号会通过数字采集芯片采集高频信号,同时削弱低于截止信号。在数字信号滤波处理过程中使用具有通带内最大平坦振幅特性的巴特沃斯滤波器(BHPF)清除低频信号,其振幅和频率关系为
(2)
式中:H为传递函数;n为滤波器级数;j为虚数单位;ω为信号角频率;ωc为截止频率。
针对某海域所积累的多井段的振动信号和实际钻井数据,运用傅里叶变换进行振动数据的处理。以一组实测数据为例,选取x轴振动信号,见图3、4。

图3 高通滤波过滤后的x轴振动信号
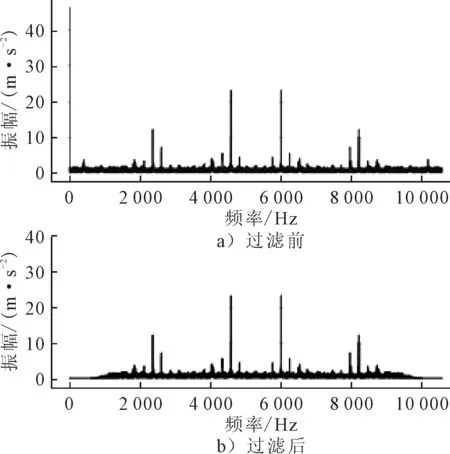
图4 高通滤波过滤前后的频域信号特征
由图3和图4可知,经过高通滤波的信号提高了信号的信噪比,频域上去除了反映钻柱运动以及冲击拍打井壁的低频噪声,仅留下反映钻头破岩信息的振动波形。
2.2 振动信号分析方法
使用傅里叶数字信号处理方法分析井下振动信号的时间域频率域特征。
2.2.1 傅里叶变换
傅里叶变换[6]表示能将满足一定条件的某函数表示成三角函数或者积分的线性组合,其定义为将可积函数表示复指数函数的积分或级数形式,变换公式如下:
(3)
式中:x为时间,s;f(x)为可积函数;ξ为频率,Hz。
构造机械旋转工况的模拟仿真信号x(t),该信号由正弦波、频率调制正弦波及信噪比为3 dB高斯噪声组成,信号表达式为
x(t)=sin(2πfsint)+2cos[2πfcost+
153.6cos(2πfFMt)]+noise(t)
(4)
式中:x(t)为生成的模拟信号;fsin=fcos=500 Hz,为正弦波主频;fFM为调制波频率,fFM=5 Hz;noise(t)为高斯白噪声。
实际信号采样频率为5 000 Hz,即采集分析1 s的信号。仿真模拟信号的时域波形见图5,频谱见图6。

图5 时域波形

图6 傅里叶变换-频谱图
由图5可见,钻头进入砾石层或硬质地层后,在井下振动严重,并进一步激化了钻头的侧向振动。与此同时,地层中的非均质砾岩也会直接导致钻头的侧向振动。由于时域信号的信噪比较低,因此,该研究在此基础上通过时频转换,在频域的基础上进行分析,实现风险预警。
2.2.2 短时傅里叶变换
短时傅里叶变换(STFT)是传统傅里叶变换的1种变形,针对非平稳信号可通过固定时间窗口截取部分振动信号提取该段信号的频率及相位信息。具体计算流程:将整体信号拆分为有限个等长的局部信号,再将傅里叶变换逐个应用到局部信号,以此将整体的不平稳信号转化为局部的平稳信号计算频域信息。短时傅里叶变换的结果比傅里叶变换会多出时间维度信息,其变换如下。

(5)
式中:x(t)为待变换信号;w(x)为窗函数。
同样根据图5所示的仿真模拟信号,给出短时傅里叶变换时频谱,见图7。
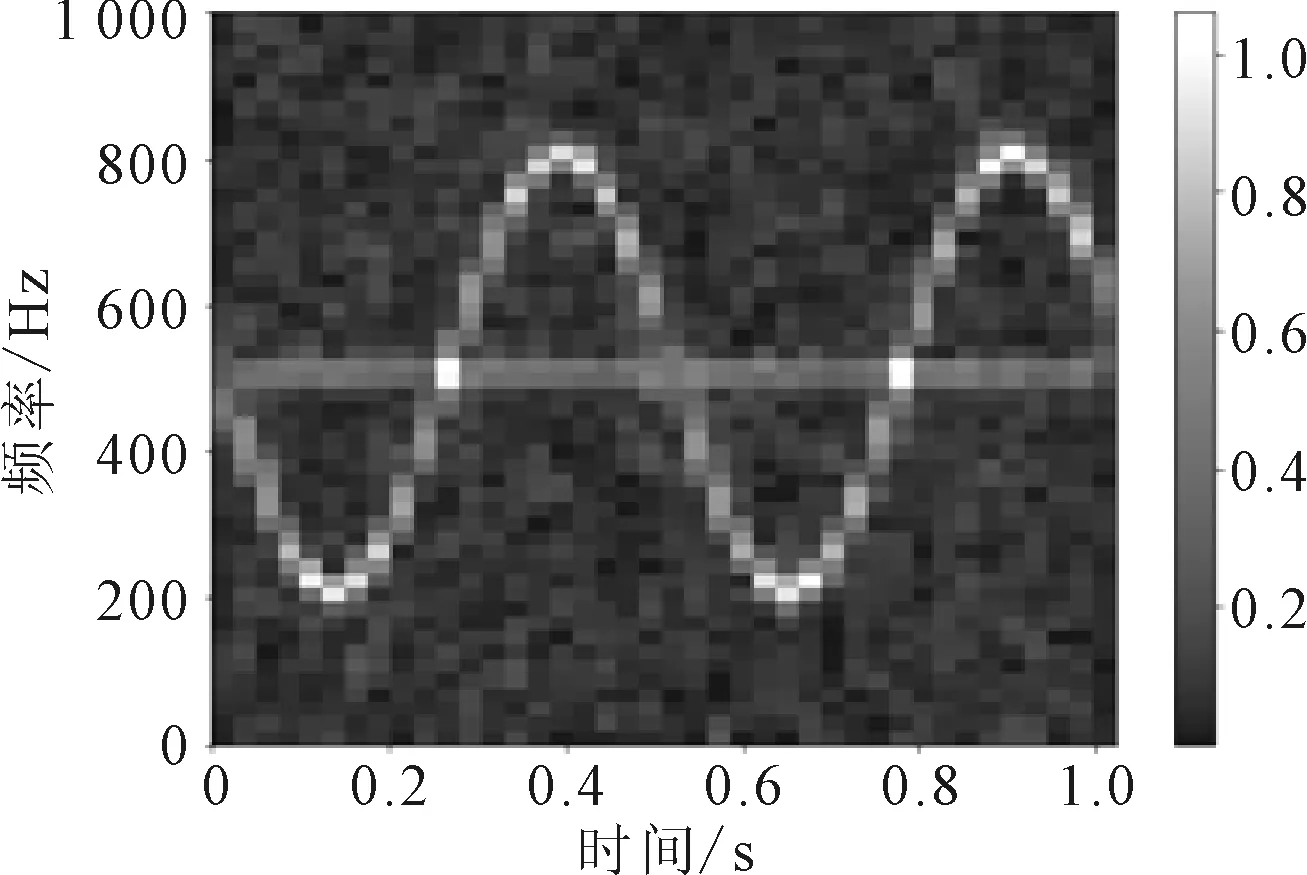
图7 短时傅里叶变换-时频谱图
由图7可知,短时傅里叶变换的时频谱图不但可表达信号的频域特征,还可体现频率随时间的变换特性。不仅可提取出500 Hz的主恒频率,还可给出随时间变换的频率分量信息。
2.2.3 小波变换
小波变换(WT)是指用有限长或快速衰减的“母小波”的振荡波形表示信号,该波形被缩放和平移以匹配输入信号。小波变换相较短时傅里叶变换,优势在于其可自适应频率变换,满足高低不同频率下的分辨率要求,并且在去噪时不会对信号造成明显破坏。其变换如下。
(6)
式中:x(t)为待变换信号;a为尺度参数;b为平移参数;Ψ(x)为小波函数。
根据图5所示的仿真模拟信号的时域波形图,给出以Cgau(复数形式的高斯小波)为小波函数的小波变换-时频谱图,见图8。
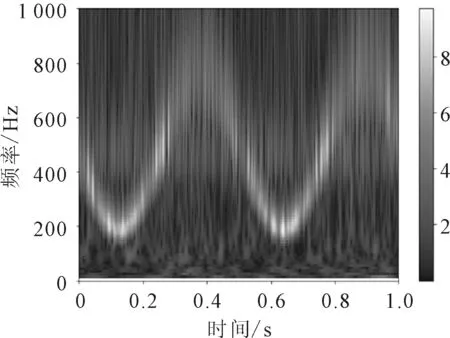
图8 小波变换-时频谱图
由图8可知,小波变换的时频谱图可表达信号的频域特征,还能体现频率随时间的变换特性。相比短时傅里叶变换的时频谱图,时频谱图的时频分辨率明显改善,低频段具有较高的时间分辨率,并且频率范围也突破200~800 Hz。
3 应用分析实例
3.1 近钻头振动时域信号特点
实验装置在某实验井内进行测试,已知该实验井段包含2处砾石层和1处硬质砂岩夹层。地质勘察井完钻后,提取近钻头振动采集装置中存储的振动信号,见图9~11。
仅通过观察3种不同岩性的时域振动样本很难区分归类岩性种类。这些地层差异较大,但振动波形相似,振幅微弱差异,因此,进一步对这些时域振动信号进行时频转换处理。
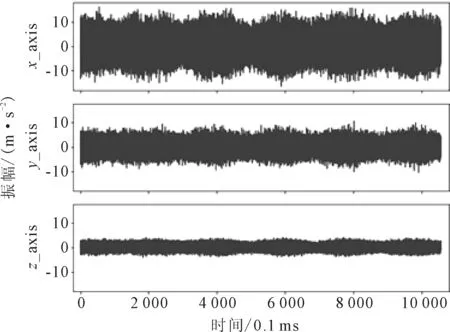
图9 砾石层时域振动信号

图10 硬质砂岩层时域振动信号

图11 泥岩层时域振动信号
3.2 振动信号频域特点
通过傅里叶变换系数得到近钻头振动的频域信号,见图12。计算得到傅里叶变换后的频谱图,岩性特征频率便于观察信号特点[7]。

图12 3种岩性典型频谱
选取3种海底地质勘察中的常见岩性中具有代表性样本的频谱进行对比,其中2种岩性则是容易导致自升式平台倾覆的以及插桩困难的硬质砂岩夹层以及砾石层。
由图12a)可知,泥岩的频谱强度在整个频段均匀分布,无特别显著的特征峰存在,由于在地质勘察钻头在泥岩中钻井时钻头吃入深度较大,以刮削和水力喷射液化为主,整个钻头的运动状态是均与平稳的。如图12b)和图12c)所示,海底地层中遇到硬夹层时,会产生明显的冲击特征。此类地层也是容易导致海洋工程建设期间插桩失败或者自升式平台倾覆的重要原因。对于砾石层和硬质砂岩夹层存在相似的特征峰,但峰值强度不同,并且砾岩的z轴方向也有强频率峰值显示,表明钻进砾岩地层时钻具会沿井筒方向产生冲击;对于砂岩轴方向的信号较弱,说明在砾石层内钻进期间,存在着较为严重的跳钻。
通过处理后的频谱图像,可以较为直观地表征不同地层的振动状态,并依据这些振动状态及时对海底存在的砾石层或硬质夹层进行预警。
4 结论
1)近钻头振动数据采集装置和算法对海底地质勘查钻井振动数据进行有效采集和存储,可为砾石层、硬质砂岩、泥岩频谱数据分析提供可靠数据基础,在不增加额外的工程勘测成本的条件下,为海底异常地层预测提供装备保障。
2)基于傅里叶变换、短时傅里叶变化等典型信号分析方法,针对井下振动数据的分析与处理提出时域信号和频域信号的特征分辨海底异常地层的分析方法,建立端到端的海底地层识别振动分析方法和分析模型。
3)基于文中研究方法对实验井进行振动数据采集,振动信号的分析处理,振动信号时域频域特征分析,可有效识别砾石层和硬质夹层,证明该方法可以将泥岩与硬质地层区分开来。
