不同湍流模型在高效舵水动力计算中的适用性分析

(上海船舶研究设计院，上海 201203)

在流场中，当流体的雷诺数达到一定数值时，流体的流动状态由层流向湍流转变。湍流是由各种大小和旋转方向随机的不同尺度涡叠合而成的流动，并且具有强烈的不规则性、耗散性和扩散性[1]，尽管湍流运动极其复杂，但实验研究表明，非定常的Navier-Stokes方程对于求解流动中各物理量的瞬时值依然适用[2]。目前，采用CFD对湍流进行模拟的方法分为直接数值模拟法和非直接数值模拟法[3]，直接模拟法通过直接求解瞬态的Navier-Stokes方程，得到湍流的脉动特征，由于计算开销非常大，因此在工程上的应用受到限制。非直接模拟法就是不直接求解湍流的脉动特征，采用简化和近似方法对湍流进行模拟，根据简化和近似方法的不同，非直接模拟法又分为雷诺时均模拟、尺度解析模拟[4]，其中基于统计平均或其他平均方法建立起来的雷诺时均模拟应用最为广泛，常用的湍流模型包括一方程Spalart-Allmaras模型、2方程模型(k-ε、k-ω模型等)、雷诺应力方程模型(RSM)。对于流动简单的流场，一般随着湍流模型方程数的增多，计算量会逐步增加，计算精度也会相应提高，但对于复杂的湍流运动，则不一定。因此，对湍流模型的适用性分析尤为必要[5-7]。

本文利用计算流体力学软件STAR-CCM+，采用5种湍流模型(Spalart -Allmaras、SSTk-ω、Standardk-ε、Realizablek-ε、RSM)对1种自行开发的新型随边扭曲高效舵进行水动力计算，并将模拟结果与在上海船舶运输科学研究所进行的敞水模型试验结果进行对比，寻求适用于模型尺度下随边扭曲高效舵水动力数值计算的湍流模型。

1 模型试验

舵的敞水试验在上海船舶运输科学研究所拖曳水池进行。水池长192 m，宽10 m，深4.2 m，试验时工作水深为4 m，水池的前端设置可以生成规则波和随机波的单摇板电液伺服式造波机，水池两侧和末端设置消波装置，水池上方设有运行速度为0.01～10 m/s的拖车系统。舵上升力FL、阻力Fd、舵轴转矩M的测量采用六分力传感器。

试验的缩尺比、工况及模型参数见表1。

注：Vm为模型试验时拖车速度；Rem为模型尺度下的雷诺数。

试验需测量各方案在不同舵角下舵的受力情况，各方案力的测量从0°～30°范围每隔5°进行一次。试验时，首先需调整舵角至相应角度；然后打开六分力测量软件，再将拖车开至工况要求的速度；最后拖车保持匀速行驶至试验结束。试验时，舵的安装图和尾流场见图1、2。

图1 舵的安装

2 数值模拟

2.1 几何模型的建立

对舵进行几何建模，见图3，在实尺度下的几何参数见表2，建模时模型缩尺比与试验保持一致。

表2 随边扭曲高效舵实尺度下的几何参数

图3 随边扭曲高效舵几何模型

2.2 计算域及边界条件

通过CFD对舵敞水特性进行模拟时，需着重分析舵表面黏性绕流情况，只需考虑其外部轮廓形状，对于流场域仅建立1个单独的长方体计算域，见图4。其中，速度入口边界距舵导边4倍弦长，用于给定来流速度；压力出口边界距舵随边7倍弦长，此处流动充分发展；计算域左右侧面距离舵中纵剖面各3倍弦长，设定为壁面边界；流域底部和顶部分别距舵顶和舵底4倍舵高，设定为壁面边界；舵表面设定为无滑移壁面边界条件。

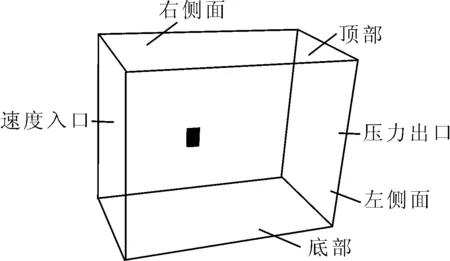
图4 计算域及边界面

2.3 网格划分

为确保计算精度和收敛情况，对网格进行无关性验证和收敛性判断，最终确定计算域网格数量为360万，网格划分情况见图5、6。

图5 计算域网格划分

图6 舵近壁区网格划分

2.4 计算输入条件

水的密度取为998.26 kg/m3，与拖曳水池中水的密度保持一致；速度入口边界给定的来流速度与物理试验时的拖车速度保持一致。模型试验时温度计测得的水温为19.2 ℃，因此,水的黏度取为0.001 029 9 Pa·s。

3 结果分析

20°舵角下舵周围流场见图7、8。

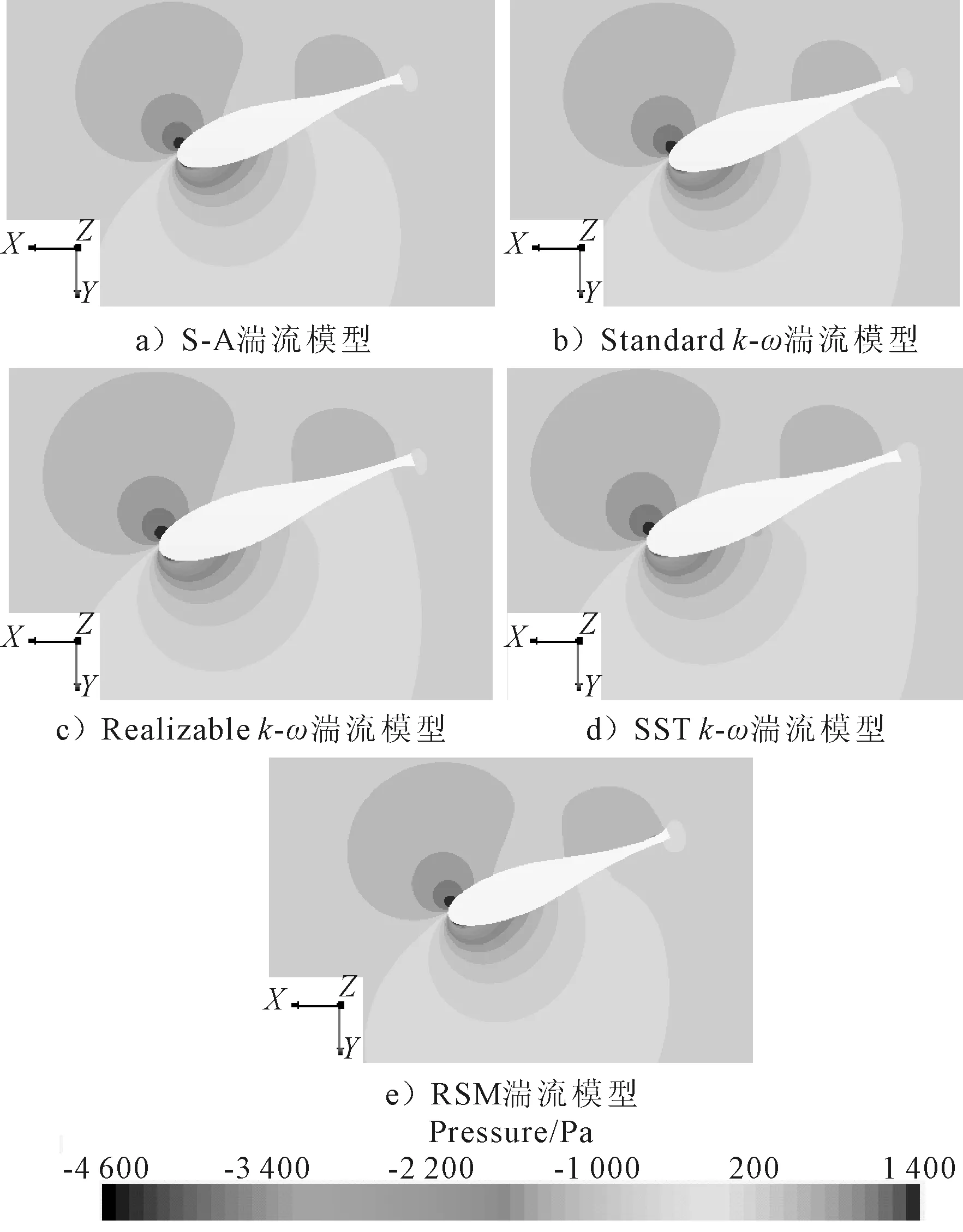
图7 舵周围流场压力分布云图

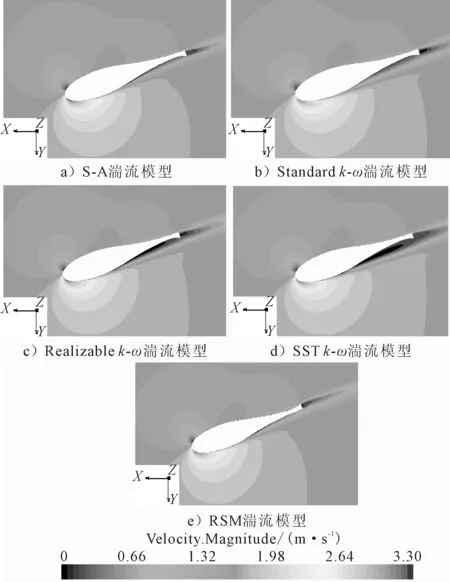
图8 舵周围流场速度分布云图

由图7可见，各湍流模型下舵压力面和吸力面周围流场的压力分布非常相近，但在部分区域略有不同，尤其在吸力面随边扭曲区域。由图8可以看出，不同湍流模型下，舵压力面侧流场的静流区域大小有所不同，其中SSTk-ω湍流模型下舵吸力面侧对应的静流区域最大。

数值计算结果与模型试验结果对比见图9。

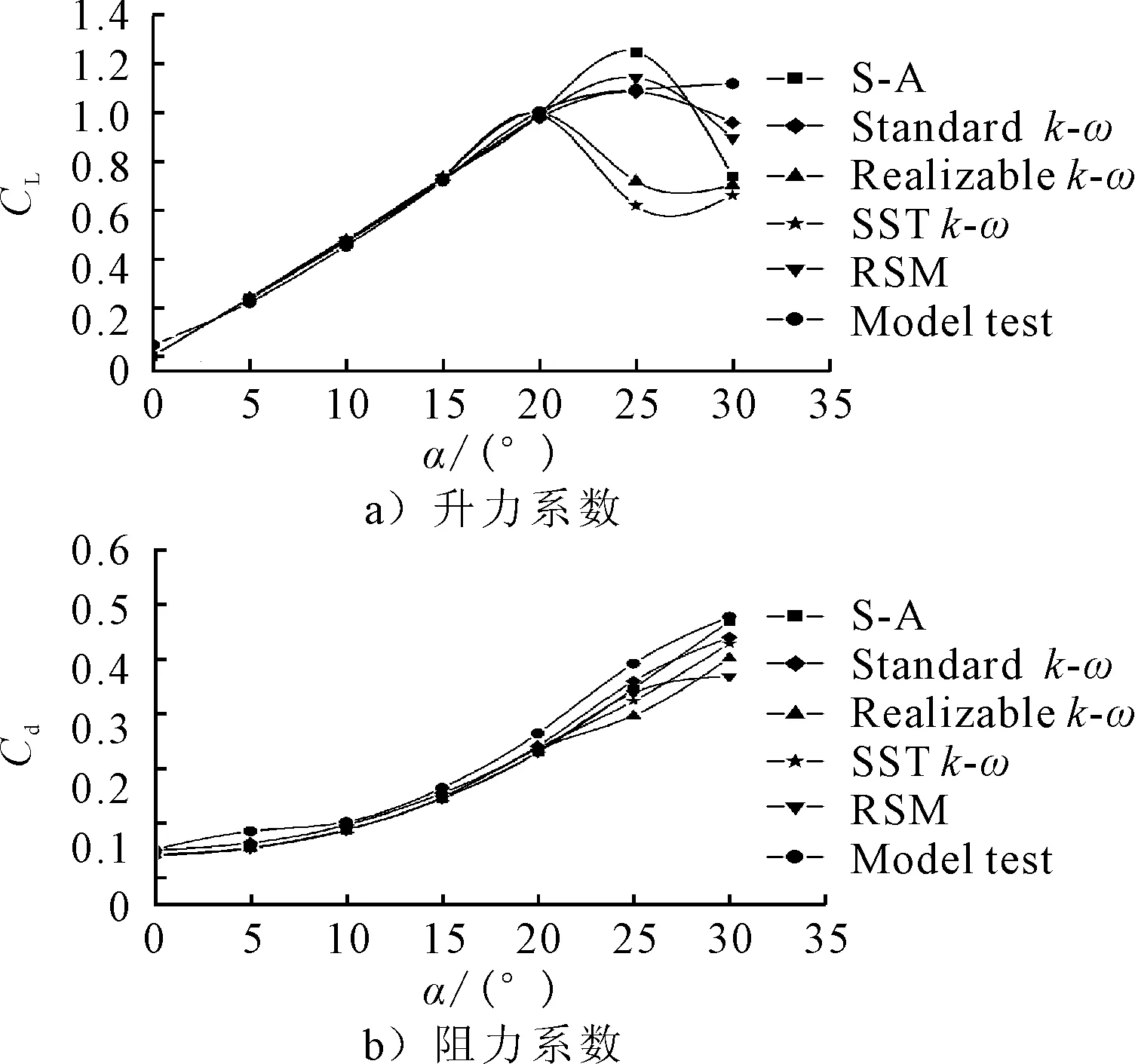
图9 各湍流模型下数值模拟结果与模型试验结果对比

由图9可见，各湍流模型下，升力曲线在失速角以前与模型试验结果均相差不大；对比发现，各湍流模型下失速角较模型试验都有所提前，其中Realizablek-ε和SSTk-ω湍流模型下失速角与模型试验相差较大；从阻力曲线的对比可以看出，阻力曲线与模型试验结果的趋势基本一致，在失速角后，各湍流模型得到的阻力系数与模型试验结果偏差较大；在所有舵角下Standardk-ε湍流模型得到的仿真结果，无论在升力系数方面还是在阻力系数方面均与模型试验结果最为接近。

4 结论

各湍流模型下，舵压力面和吸力面周围流场的压力分布非常相近，但在部分区域略有不同，尤其在吸力面随边扭曲区域；各湍流模型下，升力曲线在失速角以前与模型试验结果均相差不大，但失速角较模型试验都有所提前；阻力曲线与模型试验结果的趋势基本一致，不过在失速角后与模型试验结果偏差较大；综合来看，在所有舵角下Standardk-ε湍流模型得到的仿真结果，无论在升力系数方面还是在阻力系数方面均与模型试验结果最为接近，因此在模型尺度下随边扭曲高效舵水动力数值计算方面较其他模型更具优势。