预测电池放电终止时间的通用架构

陈培华， 聂诗良

(西南科技大学 信息工程学院，四川 绵阳 621000)

0 引 言

在自动化与智能化高速发展时期，电池的使用越来越广泛，因此，保证电池的续航能力至关重要。电池在最佳截至电压停止工作，可有利于电池使用寿命的延长，预测电池放电终止时间是一种较为科学的电池设备维护方法。在该发展趋势下的基于电池模型的预测方法越来越多。孙冬等研究者基于一阶RC等效电路模型建立的电池模型，采用反向传播BP神经网络预测算法对电池的健康状态进行预测，从SOH预测结果来看，该模型下的BP算法具有误差较为理想的优点，但计算效率低，必须求解复杂的偏微分方程组[1]；He W等研究者以DFS证据学习理论(Dempster-Shafer theory, DSF)初始化经验模型参数，再以贝叶斯蒙特卡洛(BMC)方法更新模型参数，在线获取电池电容容量进行电池剩余寿命的预测，但基于电池老化数据的经验学习不够强大[2]；Lee以电池物理学与原子模型研究，构建三维电池静态数据模型并考虑参数随时间的耦合性，在线预测实验结果表明该方法具有较强的表达电池相关参数的特性。但对于不同材料的电池，该模型并不适应，需重新构建模型，工作量极大[3]。

基于电化学模型的电池模型，具有捕获显著的电化学过程，计算效率高，可以捕获老化过程的影响等优点[4,5]。综合考虑电池的电化学模型的优点，并采用传播者—观测者—预测者的通用预测架构，可大大提高预测过程的设计开发时间，解决研究对象模型的构建分析难的问题。

1 电池的电化学模型建模

1.1 电化学模型

电池电压示意图如图1所示，因总电池电压为正极集电器的电位与负极集电器之间的差值的影响，导致电位会随着d∈[0,L]的变化而变化[6]

V(t)=φS(0,t)-φS(L,t)

(1)

图1 电池电压示意

在正极集电器处平衡电位为VU,p，由于固相欧姆电阻以及Vη,p的存在，该电压降低Vs,p，电解质欧姆电阻则导致另一个电压降为Ve。在负极集电器处，由于表面过电位，存在Vη,n压降，以及固相电阻压降Vs,n和负极集电器VU,n处的平衡电位，电压再次下降。五个电压项的主要方程式子如下。

1)平衡电位

(2)

式中VINT,i为活动修正项(理想条件下为0)，对于LixCoO2，x必须至少为0.4[7,8]。活动系数项与过量的吉布斯自由能有关，可以使用Redlich-Kister扩展来捕获，从而得到VINT,i的新表达式为

(3)

2)浓度过电位

(4)

(5)

3)欧姆过电位

由于固相欧姆电阻，电解质欧姆电阻和集电器电阻引起的电压下降可视为恒定电阻并集中在一起，表示为

Vo=iaapRo

(6)

4)表面过电位

Butler-Volmer方程描述了由于电荷转移电阻和SEI动力学(电池老化过程参数)引起的过电势[9]。过电位与电流大小成一定关系，这两个特性在Butler-Volmer方程中组合而成。方程式为

(7)

Butler-Volmer方程可以简化并以电压表示，具体的简化方程为

(8)

5)电池电压

V=VU,p+VU,n-V'o-V'η,p-V'η,n

(9)

1.2 模型参数

根据五电压项表达式参数整理，得到整个模型所需参数内容。对于18 650锂电池的电化学模型的参数:可用电量qmax为1.32×104C，通用气体常数R为8.314 J/mol/K，电极温度T为292 K，法拉第常数F为96 487 C/mol，转移电子数n为1，扩散常数D为7.0×106mol s/C/m3，参考经验时间常数τo为10 s，对称因子α为0.5，内阻Ro为0.085 Ω，正极表面积Sp为2×10-4m2，正极BV集总常数kp为2×104A/m2，正极表面体积Vs,p为2×10-6m3,正极表面总体积Vb,p为2×10-5m3,正极经验时间常数vη,p为90s,负极表面积Sn为2×10-4m2,负极BV集总常数kn为2×104A/m2,负极表面体积Vs,n为2×10-6m3,负极表面总体积Vb,n为2×10-5m3,负极经验时间常数τη,n为90 s[10]。

2 通用预测架构设计

2.1 通用预测架构框架

本文采用的通用预测架构如图2所示。

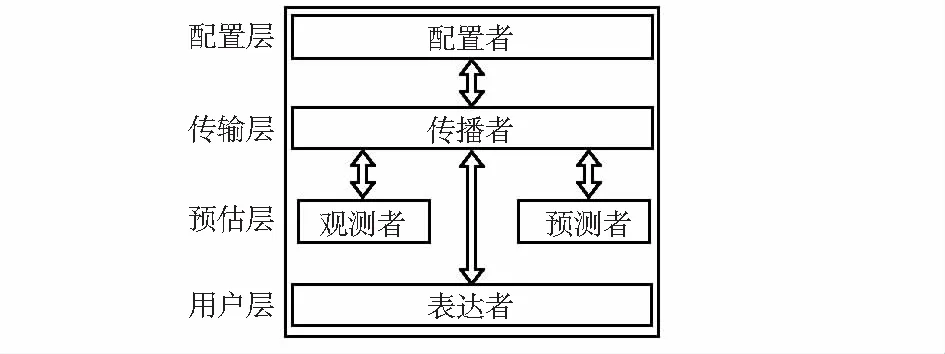
图2 通用预测架构

配置层：主要是操作配置文件，配置文件中指定设备名称、采用的模型、标签以及是否开启传播者的其他功能等。传输层：主要提供数据交互功能，承担数据交互桥梁且做指令解析、数据通路选择，可进行以太网、串口等通信方式获取实时预测数据。预估层：分为观测者和预测者，观测者进行数据滤波，滤波结果经传输层传递给预测者，进行基于模型以及滤波后可靠在线数据的放电终止事件时间预测。用户层：可对整个通用架构进行启动、暂停、恢复、停止的操控。同时，用户可在该设计层进行人机交互界面的设计，使得架构功能更加齐全。预估层提供观测者和预测者的空函数框架，为后续的滤波算法和预测算法提供函数接口，同时可测试相关算法的适用性以及可靠性。

1)观测者空函数框架：使用EmptyObserver.py函数框架进行滤波算法的设计，其中包括模型的选择、状态输入、过程噪声以及输出等参数的配置，进行该滤波算法步骤的程序设计。

2)预测者空函数框架：使用EmptyPrognoser.py函数框架进行滤波算法的设计，配置相关的输入参数，主要包括采用个数点以及预测步长和预测停止条件，根据具体预测算法步骤进行程序设计。

2.2 通用预测架构设计思路

通用预测架构整体设计思路如图3所示。

图3 通用预测架构整体设计思路

3 实验过程及结果分析

3.1 实验过程

采用新旧程度为85 %的18 650锂电池放电过程数据进行一次预测实验，软件中点击“配置文件选择”按钮加载配置文件。指定预测battery1电池设备，电池ID为“batery123a”，输入参数为电压、功率以及温度，模型采用18 650锂电池的电化学模型，预测事件为电池放电终止时间预测，并指明预测实践中电池所带负载为8 W，读入数据源文件位置为本地“batery123.txt”。根据具体的配置参数，在交互界面上进行控制指令操作执行相应的通用架构功能任务。

单击“开始”按钮进行实际的电池放电终止时间预测，示例实现效果如图4所示，经过实际的电池通用预测架构展现出电池电压的UKF滤波效果并在软件右上角实时展现出电池的放电终止时间预测结果。采样周期为1s，预测架构软件基于电化学模型的状态方程不断进行MC蒙特卡洛模拟采样预测，得出预测结果[11,12]。

图4 通用预测架构软件实现效果

为了进一步分析预测结果，测试该模型及通用预测架构的性能，提供了报表生成功能键，可进行该软件从启用到点击“报表生成”按钮事件节点的所有系统输出数据，对应生成文本文件，可用MATLAB进行数据分析[13]。对应的UKF放电电压预测(滤波)结果图如图5所示。

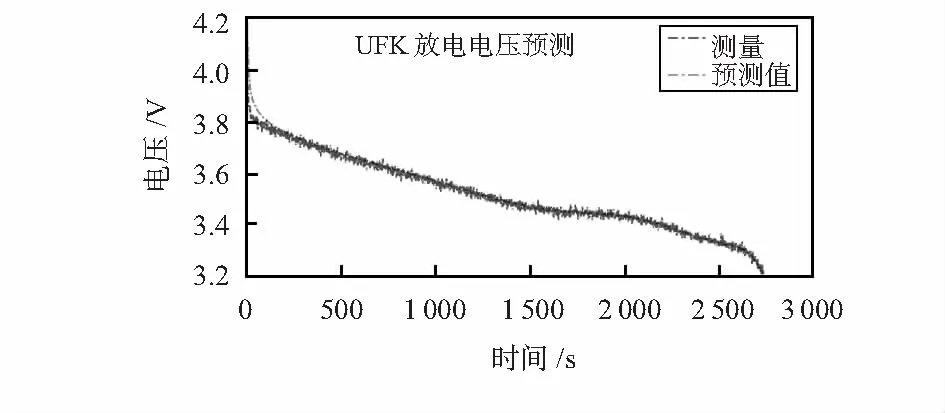
图5 UKF放电电压预测(滤波)效果

同时本次实验采用的18 650锂电池的在MATLAB数据分析功能下的放电终止预测时间分析图如图6所示。

图6 MATLAB的放电终止预测时间分析

3.2 实验分析

从图5的波形来看，预测曲线较为准确地跟踪测量曲线，图6分析图表明，整个过程预测的放电终止事件发生的时间误差最大为0.256 %，具有较高的预测精度。为进一步电化学模型适用性及预测算法实用性与可靠性，以公开的B0005电池在8 W负载下的168次循环充放过程的放电数据集为例进行本地数据在线测试，相应的测试分析表格如表2所示。

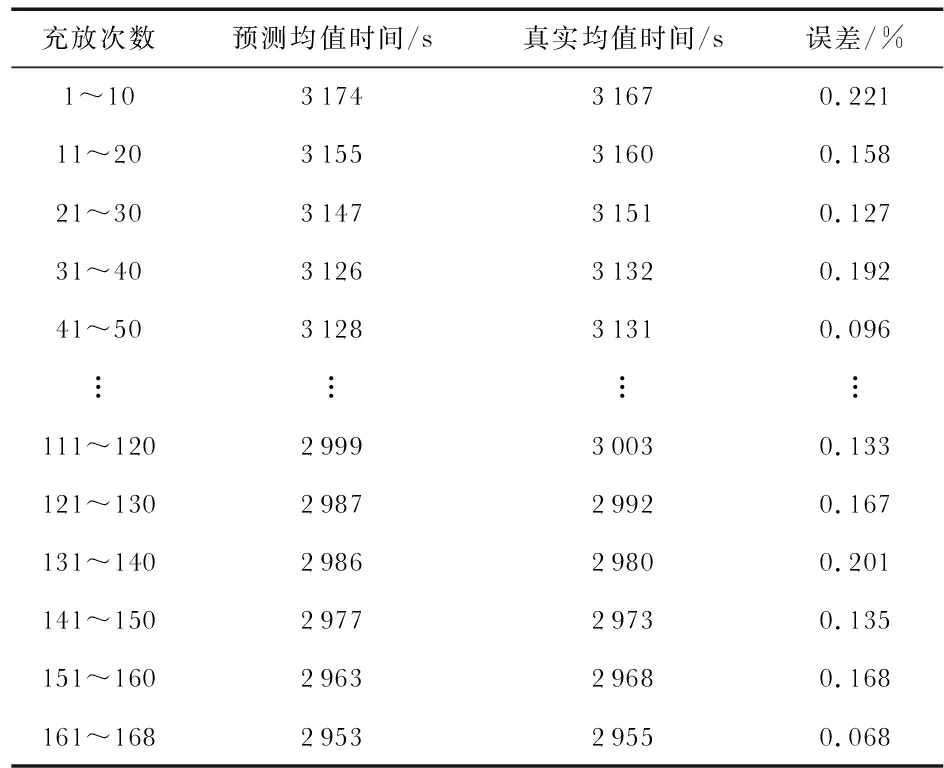
表2 168次放电终止时间预测误差分析表

从误差分析结果来看，预测的时间的真实放电终止时间误差在0.068 %～0.221 %范围内波动，与图6的18 650锂电池的一次预测结果相匹配，整个实验过程数据符合相关预测标准，具有较高的实时预测性，预测时间呈现为收敛的过程。

4 结 论

本文基于电池的电化学模型以及模块化思路构造了预测电池放电终止时间的通用架构，该通用架构具备实验部署的实用性及可靠性，所选算法及模型能够很好地跟踪电池放电过程地电压变化及电池老化过程，较准确地预测电池的放电终止时间。基于电池电化学模型的预测放电终止时间的通用架构的实现，可很大程度地减少在电池放电终止预测的程序设计思路及研究时间，整个设计实现过程为电池设备维护提供了科学的方法。在可信范围内能准确地预测电池放电的终止时间，在预知该事件快发生的情况下，准确地采取结束放电过程的措施，在一定程度上可提高电池循环使用次数，延长电池的使用时间。